飞艇用层压织物类膜材中心撕裂破坏机理模型
2016-08-06陈建稳陈务军高成军何世赞
陈建稳, 陈务军,周 涵,高成军,何世赞
(1. 南京理工大学 理学院,江苏 南京 210094; 2. 上海交通大学 空间结构研究中心,上海 200030)
飞艇用层压织物类膜材中心撕裂破坏机理模型
陈建稳1, 陈务军2,周涵1,高成军2,何世赞2
(1. 南京理工大学 理学院,江苏 南京 210094; 2. 上海交通大学 空间结构研究中心,上海 200030)
摘要:中心撕裂破坏是飞艇用层压织物类膜材失效破坏的基本形式之一. 基于层压织物类膜材的平纹织物结构特征,建立了具有平面纱线结构的中心切缝撕裂机理模型,该模型应用了“等效纱线”及“应力集中渐变区”两个概念,分别实现模型参数的简化和应力集中区域应力场分布的细化. 运用所提机理模型实现了对不同切缝长度时(10~40 mm)经纬向层压织物类膜材撕裂破坏行为特征的预测,分析了蒙皮材料撕裂扩展机理,并结合试验结果证实了模型预测的精确性和可行性. 由模型分析获得了蒙皮材料在渐变区推移过程中的撕裂承载力及变形特征,发现纱线的失效应变、弹性模量以及编织密度等是影响蒙皮材料撕裂抗力的主要因素. 所得结论及研究方法可为层压织物类膜材的强度设计、裂纹止裂分析及结构的安全性评估提供理论参考.
关键词:层压织物; 中心切缝撕裂; 撕裂机理; 应力集中渐变区; 等效纱线
层压织物类膜材是充气膜结构的主要材料类型,具有高强、轻质、性能稳定、气密性优等特点,现主要用于平流层飞艇的蒙皮结构.
平流层飞艇凭借静升力驻空,由于具有高空侦察、通信中继和空间探索等诸多领域的应用优势,成为美国、欧盟、日本等世界主要军事大国研究的热点[1-9]. 轻质高强的蒙皮材料广泛应用在飞艇的主(副)气囊、尾翼等关键部件中,其物理力学特性对飞艇的结构性能及飞行控制至关重要[2-3,5].
在飞艇结构组装或工作过程中,由于尖利物刺破、高低温交变、高超压、纤维纬斜和弓曲、材料固有缺陷、拼接热合等因素,不可避免会引入裂纹或孔隙等缺陷. 只要缺陷邻域附近的应力水平足以使裂缝发生扩展,张紧的蒙皮材料就存在失效的危险. 撕裂破坏是飞艇结构失效破坏的基本形式之一,因而蒙皮材料存在初始裂纹时的撕裂力学性能受到重点关注[6-10].
目前,对织物类膜材的撕裂试验及理论分析一直是国内外学者的研究热点[11-29]. 从撕裂形式上,多数研究集中于梯形撕裂、舌形撕裂等形式[3-7],对中心撕裂形式[8-9]的研究较少. 飞艇蒙皮的撕裂分析方法[30]与其他织物类膜材的分析方法不同,在国际上飞艇蒙皮撕裂试验一般采用中心切缝撕裂方式,该方式最先由美国空军采用. 由于中心切缝撕裂方式在展现充气蒙皮材料的撕裂行为方面,优于梯形或舌形等方式,可有效测试蒙皮材料的撕裂性能,因而得以在蒙皮材料上应用和推广,有关蒙皮材料的检测方法[30]和标准[31]均采用中心切缝撕裂方式.
从研究方法上,多数研究以试验分析[8-12]为主.对膜材撕裂机理研究,在梯形、舌形撕裂等形式上研究[5,7,16-17]较深入,对中心切缝撕裂破坏机理的研究还不足,尤其在切缝扩展及撕裂强度的衍变机理方面尚未见文献发表. 对于应力集中区域,大多研究采用简化的应力三角区模型[10,15],三角区模型对应力集中区的应力分布考察不足,对应力集中区的应力分布特征有过简化的嫌疑.
本文针对中心撕裂形式建立裂缝扩展分析模型,对蒙皮的中心切缝扩展历程及承载力变化规律进行详细分析,深入探讨带中心切缝蒙皮材料的撕裂破坏机理. 将膜材的材料非线性纳入切缝撕裂响应分析中,对应力集中区的应力分布进行细化,提高模型对蒙皮材料撕裂响应预测的准确性,从而更全面地了解材料的力学性能.
1材料和试验
1.1蒙皮材料及试件尺寸
1.1.1蒙皮材料
试验材料为热致液晶(LCP)芳族聚酯类膜材Uretek3216LV®,主要由Vectran®基布和聚氟乙烯(PVF)面层及各功能膜层复合而成. Uretek3216LV膜材是新型高性能蒙皮材料的代表,广泛应用于国内外大中型飞艇、航天领域[7,32-33].
Uretek3216LV厚度为0.21mm,面密度为200g/m2,其织物组成结构如图1所示. 织物为平纹组织结构,其经纱与纬纱垂直相交,织物经、纬向密度分别为17和12根/cm,纱线线密度为222 dtex. 膜材的黏贴层为丙烯酸化合物,具有良好的弹性性能.

图1 层压织物类典型组成结构示意Fig.1 Typical laminated fabrics layout
1.1.2试件尺寸
参照文献[30]进行试件制作,试件尺寸如图2所示. 试件的长、宽分别为152.4和101.6mm,两者有效尺寸分别为76.2和101.6mm. 切缝位于试件中心,共4组梯度长度,分别为10,20,30,40 mm;每组类型均做3个试件,以获得具有代表性的撕裂性能.

图2 撕裂试件尺寸(mm)Fig.2 Dimension of tearing specimens(mm)
1.2中心撕裂试验
试验环境参考ISO139—2005,实验室相对湿度为(65±4)%,温度为(20±2)℃. 试验设备采用CHA-20KN型MINEBEA拉伸试验机,本试验机可进行单调拉伸、剥离、撕裂3种试验,拉伸速率为1~200mm/min. 试验过程中记录试验的荷载-位移数据,加载速率为1mm/min.
2机理模型分析
2.1模型假设
蒙皮材料的抗撕裂承载力由纱线基布和各功能层共同提供,在模型计算时将作如下假设.
(1) 各功能膜层在加载过程中承载力较小,模型中不区分各功能膜层的承载作用,统一归于PVF层承载作用项.
(2) 当受力方向纱线达到断裂应力时,PVF层也达到断裂应力. PVF层协助纱线共同承担载荷,PVF层的协助作用可附加于受力纱线上,使受力纱线成为“等效纱线”,且忽略“等效纱线”间的摩擦效应.
(3) “等效纱线”的应力-应变关系满足膜材单调拉伸试验结果(加载速率为1mm/min),考虑到其非线性特征,这里采用三折线模型(如图3所示),模型的基本参数如表1所示.
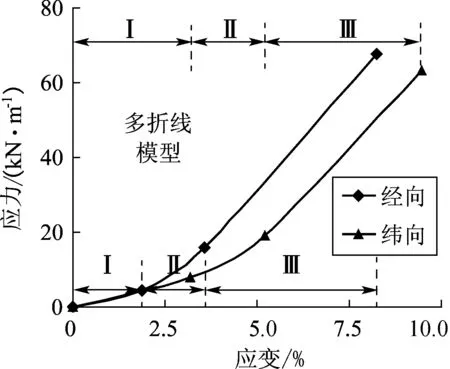
图3 应力-应变曲线Fig.3 Relationship between stress and strain
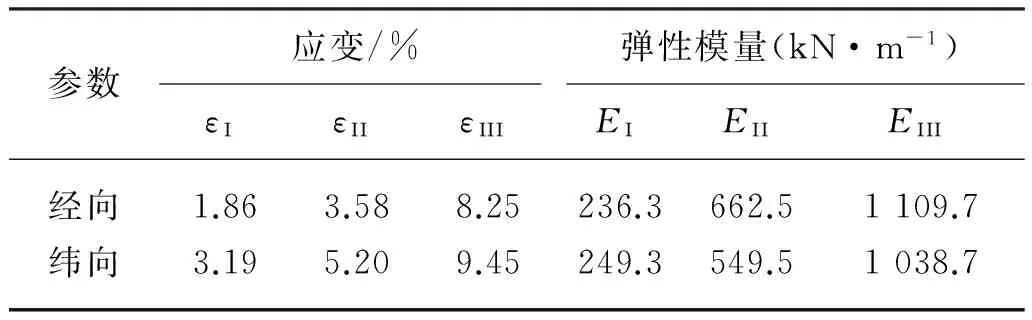
参数应变/%弹性模量(kN·m-1)εΙεΙΙεΙΙΙEΙEΙΙEΙΙΙ经向1.863.588.25236.3662.51109.7纬向3.195.209.45249.3549.51038.7
(4) “等效纱线”断裂的失效判断,采用第一强度理论即最大拉应力理论,当纱线的拉应力达到极限拉应力σult时,发生断裂.
(5) 在切缝邻域的应力按应力场理论采用指数函数形式[18](如图4所示):
σ(x)=σ0+ca·e-cb·x
(1)
式中:σ0为未引入切缝时的应力;ca和cb为表述切缝端部邻域应力集中的参数.

图4 切缝端部邻域的应力场Fig.4 Stress field in the vicinity of the slit
2.2几何模型
变形区域的等效纱线可分为两类:直接承载,起主要受力功能的纱线,称为主纱;非主要受载纱线,称为辅纱. 纱线应力-应变关系满足多段线性假设(如表1所示), 采用的物理模型如图5所示.
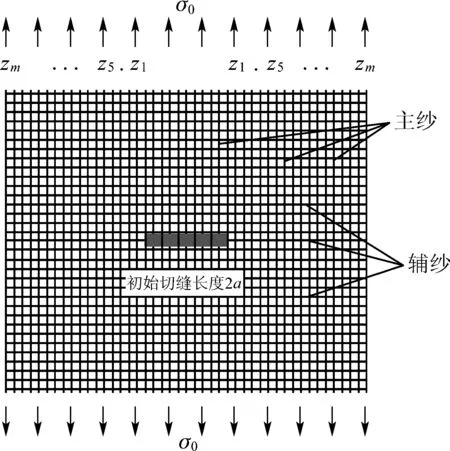
图5 中心切缝撕裂模型Fig.5 The physical tearing model for central tearing
在拉力作用下,切缝处最先张开,随着载荷的增加,其张开口逐渐增大,裂纹尖端处第1根纱线变形及受力均最大;随着切缝开口的扩大,与第1根相邻的主纱线也逐渐被拉长,依次第2, 3,…,p根纱线被拉长,如此形成两个受力渐变区. 渐变区内第2根及后续纱线的应力迅速降低,到第m根纱线时变形及应力接近均值,如图6所示. 此处1~m根所包范围即为“应力集中渐变区”,m与裂纹尖端邻域的应力场分布、裂纹尖端应力集中程度及应力均匀的判断依据有关.

(a) 切缝区域加载变形
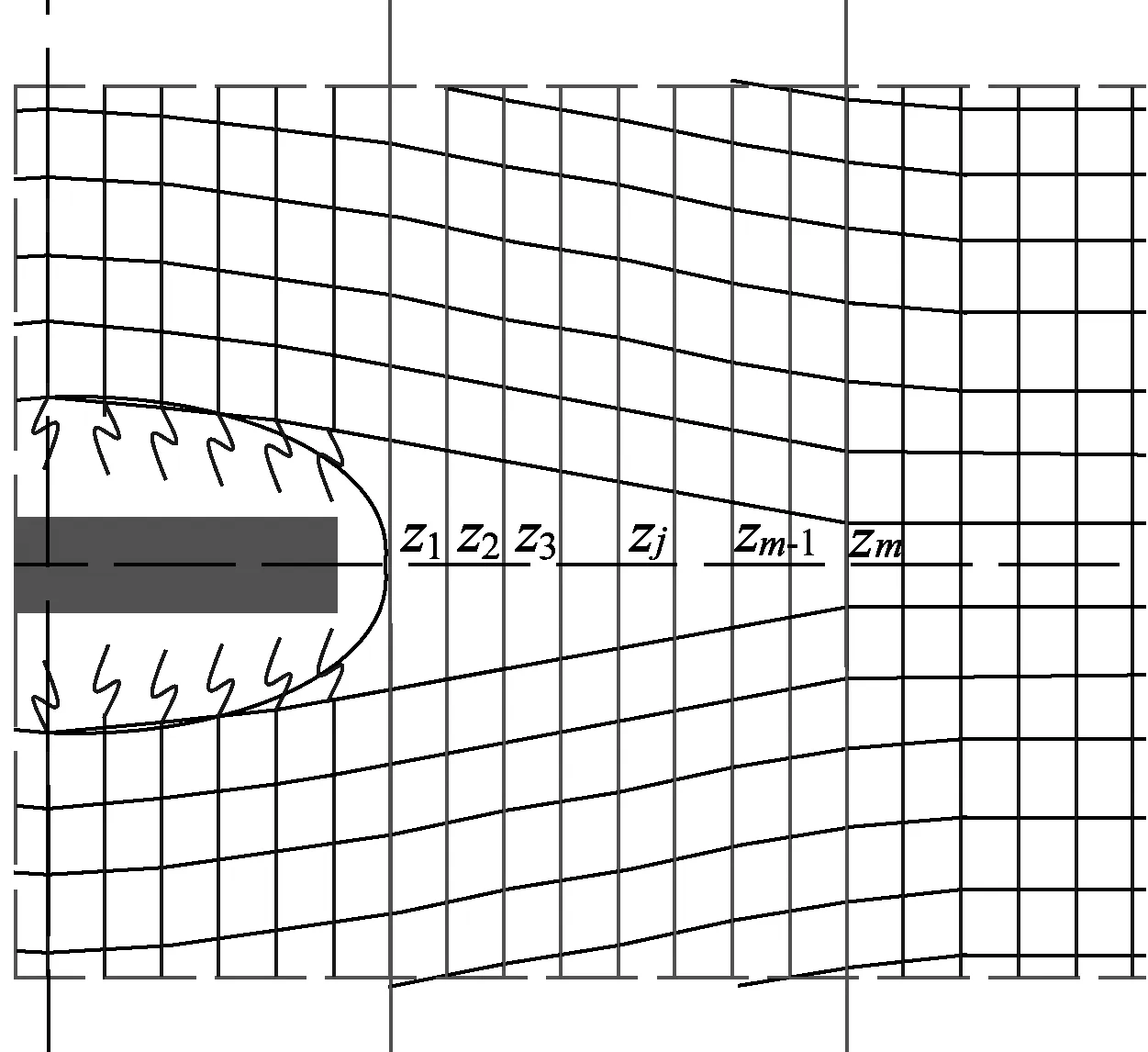
(b) 应力集中渐变区

(c) 试验图像
results of notched specimens
图6展示了模型中纱线分区情况与材料试验图像,按照纱线的受力状态及受力水平,将纱线划归入3种区域:一个已开裂区(长度2lc)、两个应力集中渐变区(长度lb)及两个应力均匀区(长度la). 已开裂区应力通过辅纱及相关区域各功能层的剪应力作用,传递到非裂纹区,并且沿着裂纹扩展方向,应力集中程度逐渐减弱. 由于辅纱的柔性特性,在裂纹尖端应力集中渐变区的最前端,辅纱传递的剪应力作用已很小,本模型忽略主纱zm+1及其之外的应力集中效应. 对于应力均匀区,可认为辅纱几乎不传递剪切应力,主纱被同步拉伸伸长 (如图6(c)所示).
由图6(b)可知,随着拉伸载荷的持续增大,构成应力集中渐变区的第一组主纱应力增加至断裂极限应力时,此组主纱发生断裂破坏,此时对应的拉伸载荷即为蒙皮材料的临界撕裂抗力. 断裂后第一组纱线z1松弛,同时第二组z2主纱延续第一组纱线z1的受力状态,出现第二个撕裂抗力峰值;如此继续下去,主纱依次发生断裂,出现数个撕裂抗力峰值,直至试样完全撕裂破坏. 在所有撕裂抗力峰值中,最大的抗力值称为最大抗撕裂力或者极限抗撕裂力.
2.3渐变区应力及分布范围
2.3.1应力分布调整
应力场理论(式(1))适用于各向同性材料,而蒙皮材料由于剪切模量较小且材料正交异性特征,应力场分布和公式的预测不可避免地存在差异. 本文结合有限元分析(FEA)对应力分布公式进行适当调整.
图7为有限元分析的应力分布结果,材料性质采用正交异性参数,弹性模量按照表1中EΙΙΙ,泊松比和剪切模量按双轴拉伸试验结果确定,泊松比为0.22,剪切模量为60 kN/m. 图7对应的切缝长度为20 mm, 加载位移为5.6 mm.
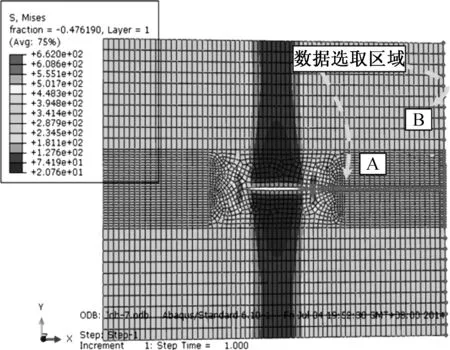
图7 有限元分析的应力分布结果Fig.7 The stress distribution of the FEA model
不同切缝长度时,有限元分析与应力场理论公式沿图7中A路径的应力分布特征如图8所示. 由图8可知,应力场理论和FEA结果在应力分布的变化趋势上基本一致,但前者的应力集中范围及应力集中程度大于后者,有必要对理论假设的参数进行适当调整,以提高假设理论在蒙皮撕裂响应分析时的精确性. 结合FEA结果,应用最小二乘法拟合原理,得出裂纹尖端处沿x轴方向(即图7中路径A)的应力分布公式:
σ(x)=σ0·(1+caI·e-cc·cb·x)
(2)
式中:参数caI和cc,经向时数值分别为1.140和2.262, 纬向时数值分别为0.960和2.341;参数cb经、纬向分别为0.110 6和0.107 5,单位为1/mm;x为应力点距裂纹尖端的距离.
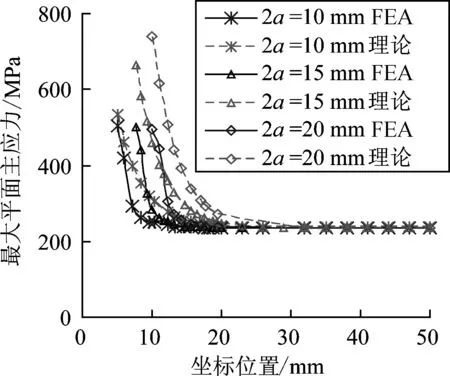
(a) 调整前
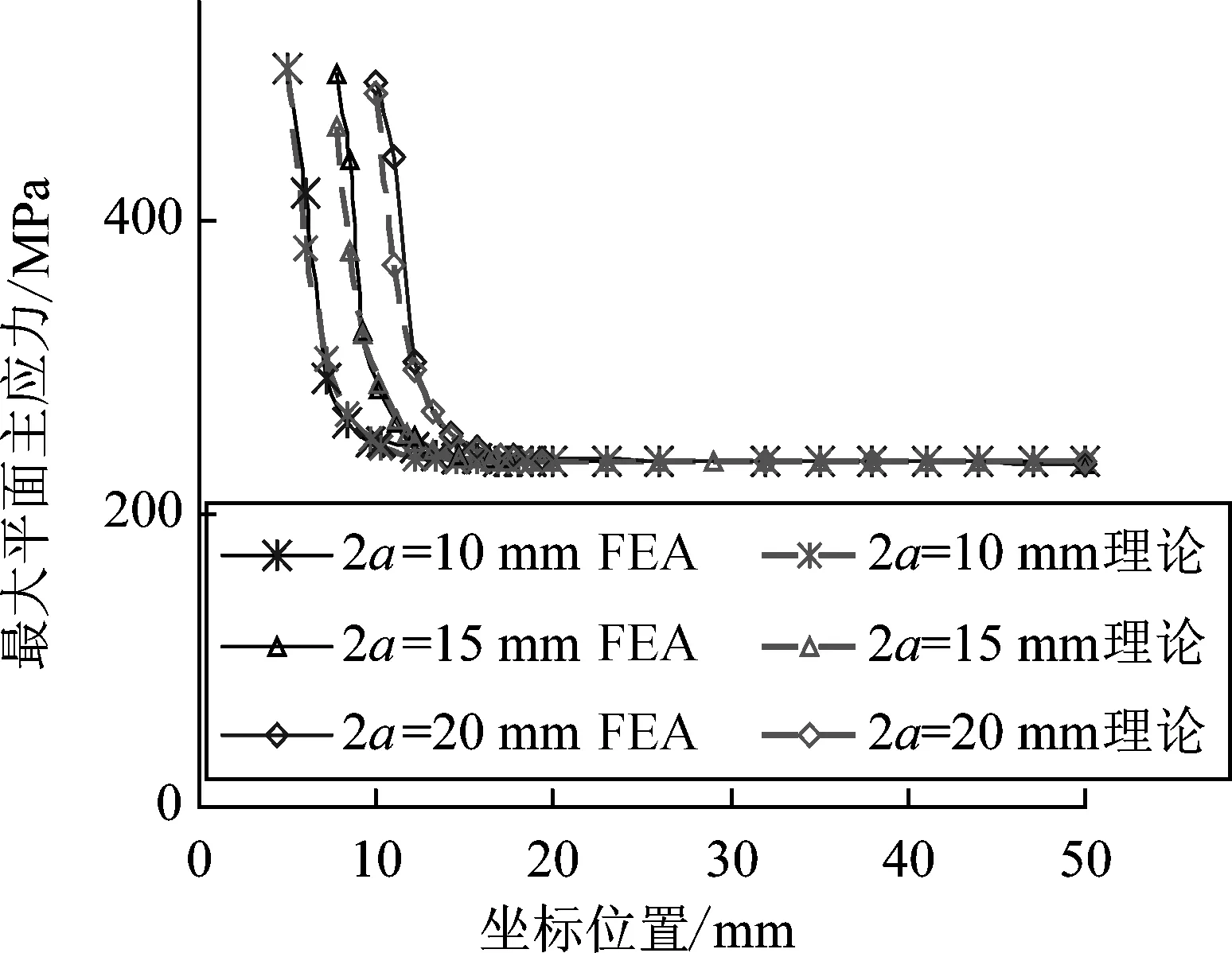
(b) 调整后
analysis and theoretical formula (warp)
2.3.2应力集中渐变区范围
由式(2)得误差η:
(3)
令η≤2.0%,可得x≤9.02 mm(经向),x≤8.61 mm(纬向). 即以2.0%的误差为标准时,渐变区范围lb≈9.0 m, 该区域内的主纱根数m为
m=lb·nc
(4)
式中:nc为主纱的编织密度,根/mm. 经、纬向nc分别为1.7和1.2根/mm,因m取整数,则经、纬向m分别为16和11根.
2.4模型撕裂抗力分析
2.4.1应力均匀区
位移载荷逐级施加,若第i-1步施加位移Δsi-1后,应变为εi-1,应力为σ0i-1. 第i步时两夹具间位移增量为Δsi,在确定主纱应力应变时,依据表1,等效纱线弹性模量按应变范围划分为3级:EΙ,EΙΙ及EΙΙΙ. 应变εi和应力σ0i表达式为
(5)
式中:E依据应变范围由表1确定.
应力均匀区所有主纱应力之和Fa-i为
Fa-i=2∑σ0i·δx=2σ0ilai-1
(6)
式中:σ0i为应力均匀区(长度为2lai)的应力;δx为等效纱线横截面宽度;lai-1为第i-1步均匀区长度.
第i步应力均匀区的长度lai和第i-1步存在如下关系:
(1) 若应力集中渐变区纱线应力σi<σult,则均匀区长度:
lai=lai-1
(7)
(2) 若应力集中渐变区纱线应力σi≥σult,则均匀区长度:
(8)
式中:pi为第i步应力集中渐变区发生断裂破坏的纱线根数.
2.4.2应力集中渐变区
第i步时在应力集中渐变区,裂纹尖端应力集中渐变区底边第1根主纱编号为z1,其应力为σi-1,其余按相同规律,第j根主纱编号为zj,应力为σi-j,直至渐变形尖端的主纱编号为zm,应力为σi-m. 对于应力均匀区的主纱,第i步时应力为σ0i.
应力集中渐变区的第j根纱线距裂纹尖端的距离xj满足以下关系:
(9)
根据式(2),可得第j根纱线应力:
σi-j=σ0i·(1+caI·e-cc·cb·(j-1)/nc)
(10)
应力集中渐变区所有纱线应力之和Fb-i的计算,有两种情况:
(1) 若应力集中渐变区所有主纱应力σi-j<σult,则
(11)
式中:σ0i为应力均匀区主纱应力;m为应力集中渐变区纱线根数.
(2) 若应力集中渐变区主纱编号j=1,2,…,pi的应力σi-j≥σult,则令σi-j=0(j=1,2,…,pi),由此合力为
(12)
2.4.3主纱合力及极限撕裂抗力计算
主纱合力的计算则需要考虑到层合织物膜材的撕裂破坏过程(如图9所示). 由于对称关系,仅画出一半模型.
破坏过程可描述如下:(1) 初始阶段(图9(a)),裂纹闭合,主辅纱线保持平直状态,彼此垂直. 随着载荷的逐步施加(图9(b)),主纱开始承担载荷,并逐渐伸长,其中裂纹附近的纱线伸长率最大,逐渐形成第一个应力集中渐变区,此时撕裂抗力由渐变区和均匀区共同承担. (2) 载荷继续增加,应力集中渐变区的纱线应力逐渐接近断裂应力,当达到断裂应力时,渐变区底边纱线出现断裂(图9(c)),渐变区开始外移,均匀区主纱数目开始减小,此时撕裂抗力由渐变区未断裂主纱及均匀区主纱共同提供. (3) 随着渐变区的外移,模型重复数次从图9(b)到图9(c)的过程,渐变区主纱依次断裂,均匀区主纱数量继续减小,直至均匀区长度为零,最后一个渐变区形成,即图9(d)状态,自此时开始,撕裂抗力仅由渐变区主纱提供,并且随着载荷的继续施加,渐变区未断裂主纱数量逐渐减小到零,模型失去承载能力.
模型在从图9(b)到图9(c)的重复变化过程中,撕裂抗力存在起伏现象. 在所有撕裂抗力数值中,首组应力渐变区中的第一组纱线断裂时所对应合力为临界撕裂抗力Fcr;在所有合力中,数值最大者即为极限撕裂抗力Fmax.Fcr和Fmax是撕裂试验分析时获取的两个重要数据,是指导柔式飞艇结构设计与分析时的重要参数.
按照模型撕裂发展过程,第i步时撕裂抗力Fz-i分下述3类情况.
(1) 若应力集中渐变区所有主纱应力σi-j<σult,且应力均匀区长度lai-1>0,对应图9(b):
Fz-i=Fa-i+Fb-i+Fc-i=
2σ0ilai-1
(13)
(2) 若应力集中渐变区主纱编号j=1,2,…,pi(pi≤m)的应力σi-j≥σult,且应力均匀区长度lai-1>0,令σi-j(j=1,2,…,pi),对应图9(c):
Fz-i=Fa-i+Fb-i+Fc-i=
2σ0ilai-1
(14)
(3) 若应力集中渐变区主纱编号j=1, 2, …,pi(pi≤m)的应力σi-j≥σult,且应力均匀区长度lai-1≤0,令σi-j=0(j=1,2,…,pi),对应图9(d):
Fz-i=Fa-i+Fb-i+Fc-i=
(15)
若pi=m,则应力集中渐变区主纱全部断裂,蒙皮材料彻底断开,合力为零.
由式(13)~(15)可知,纱线的应力水平及纱线的编织密度等是影响蒙皮材料撕裂抗力的主要因素. 此外,根据纱线失效判据,纱线的失效应变及弹性模量决定其应力水平,进而可影响蒙皮材料的撕裂抗力.
3结果及讨论
切缝长度不同时,模型预测曲线及试验结果对比如图10所示. 应力为撕裂抗力除以膜材初始净宽度.
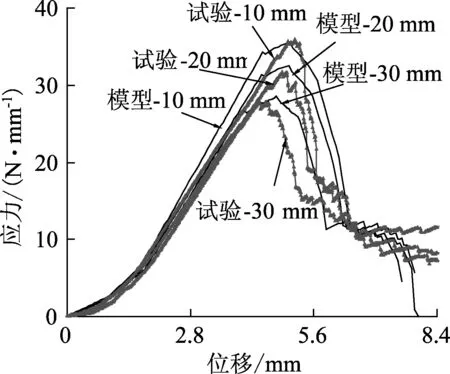
(a) 经向
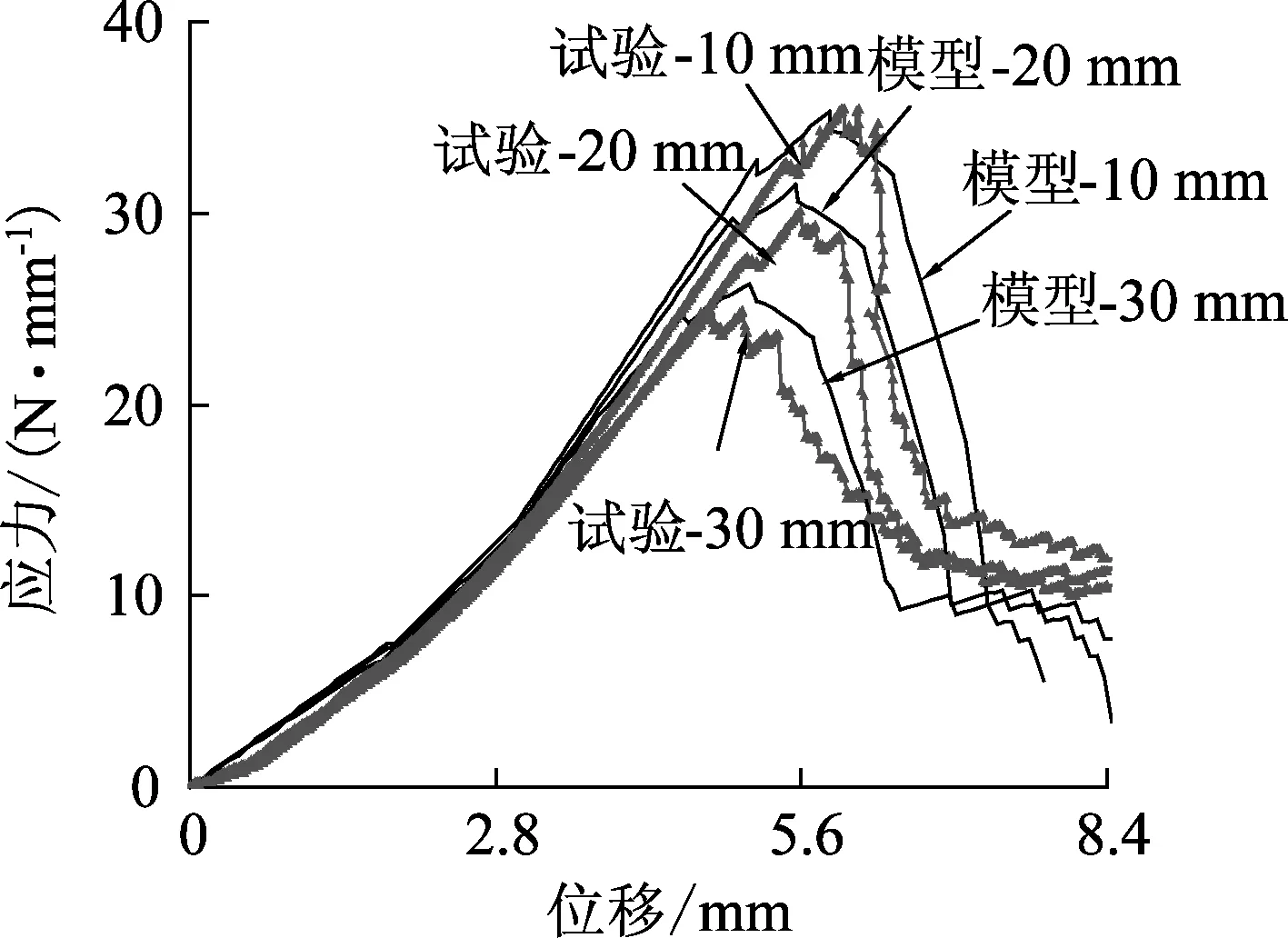
(b) 纬向
由图10可知,模型预测曲线和试验曲线在衍变趋势、数值大小、所处阶段均较接近,尤其在峰值之前,二者数值变化非常一致,模型可有效展现撕裂应力的变化规律,对应力大小、转折变化、起伏特征,均有较好的预测能力.这表明本文的撕裂机理模型在预测蒙皮材料撕裂性能时具有较好的适用性和精确性.
针对典型的中心撕裂曲线,本文提出5个特征段分法,如图11所示. 具体的分段及撕裂扩展机理描述如下所述.
OA:低斜率段.纱线和各功能膜层初始受拉,共同变形,弹性模量较低,变形发展较快,基本上和单调拉伸特征曲线的前两个低弹性模量阶段对应(见图3).

图11 典型预测曲线分段Fig.11 Typical curves of analytical model
AB:高斜率段.纱线和各功能膜层被继续拉伸,蒙皮材料处于承载强度快速上升期,纱线的力学性能逐渐起到控制作用,因主纱的弹性模量较高,曲线斜率明显大于OA段,应力随变形增加较快,应力集中渐变区主纱的应力达到极限强度时,将出现断裂现象,此时应力对应临界撕裂强度.
BC:起伏平台段.自渐变区的主纱发生破断现象后,渐变区将逐步外移,应力均匀区的长度开始减小.由于变形的增长,应力均匀区主纱应力水平仍继续增加. 应力集中渐变区主纱陆续断裂失效,蒙皮总承载强度在保持高水平的同时起伏不定,在起伏变化的过程中,存在一个峰值,该峰值对应膜材的最大抗撕裂强度. 在高应力水平的平台阶段,大量主纱储蓄了高应变能,并急剧释放,然后新的主纱又快速积聚高应变能,虽和低碳钢的屈服段机理不同,但承载强度的变化特征十分类似,起伏平台段正是蒙皮织物膜材的撕裂“屈服段”.
CD:快速下降段.随着变形的增大,渐变区断裂失效的主纱数量急剧增加,渐变区推移速度加快,使得应力均匀区的长度减小加速,蒙皮处于承载强度的快速衰退期.
DE:峰后起伏段,亦称“残余强度段”.经历快速衰退期,应力均匀区的主纱数量所剩无几,渐变区的主纱起主要承载作用,和图9(d)的最后一个渐变区的出现基本相当,该阶段渐变区主纱的断裂失效,使得蒙皮材料承载强度阶梯般衰减,并最终失去整体承载能力.
但模型与试验结果也存在差异性,主要现象及分析如下所述.
(1)BC起伏平台段.模型预测峰值起伏幅度小于试验值. 预测模型依据式(2)对纱线进行失效判断,渐变区主纱的断裂失效根数,在该平台阶段并未发生剧烈的震荡. 但在试验中,存在多根主纱齐断的现象,齐断使得应力峰值出现较大幅度的起伏.
(2)DE峰后起伏段.和试验曲线相比,模型预测曲线数值上一般小于试验曲线,并且预测曲线的下降速度较大. 原因概括为两条:一是撕裂后期,应力集中渐变区范围存在扩大的趋势,峰后起伏段的承载主纱根数多于模型假定值,因此试验时承载强度比模型预测结果要大;二是试验时高应力的作用使得主纱和其他功能层间的黏结作用减弱,主纱和其他功能层间出现滑移现象,部分主纱是被抽出膜材的,主纱并不会很快断裂失效,因此膜材的承载力下降速度会小于模型预测值.
4结语
本文基于层压织物类膜材的平纹结构特征,提出了中心切缝撕裂机理模型,实现了对层压织物类膜材的中心切缝撕裂响应的预测分析,获得了蒙皮材料撕裂承载应力-应变及撕裂扩展机理特征. 主要结论如下所述.
(1) 将织物纱线及各功能膜层整合为等效纱线进行膜材撕裂性能分析具有可行性.
(2) 针对蒙皮材料Uretek3216LV的力学性能特点,提出了等效纱线的三折线材料模型. 所提三折线材料模型,可有效跟踪蒙皮材料撕裂时非线性响应特征,实现对撕裂强度、变形特征的预测分析.
(3) 纱线的失效应变、弹性模量以及编织密度等是影响蒙皮材料撕裂抗力的主要因素.
(4) 蒙皮材料的中心切缝撕裂响应特征,在临界撕裂强度之前,主要由蒙皮材料的单调拉伸性能控制. 在出现纱线断裂后,撕裂强度存在类似低碳钢屈服段的起伏平台阶段,它是由最初几个应力集中渐变区形成和移动造成的.
所提模型可有效揭示平纹编织蒙皮材料的撕裂扩展机理,预测蒙皮材料的撕裂强度和变形特征,可为飞艇蒙皮材料的强度设计及结构的安全性评估提供理论指导.
参考文献
[1] 甘晓华.飞艇技术概论[M].北京:国防工业出版社,2005:15-36.
[2] 顾正铭.平流层飞艇蒙皮材料的研究[J].航天返回与遥感,2007, 28(1):62-66.
[3] KOMATSU K, SANO M A, KAKUTA Y. Development of high-specific-strength envelope materials[C]// 3rd AIAA’s Annual Aviation Technology, Integration, and Operations (ATIO) Tech. Denver, Colorado, 2003: 6765-6771.
[4] MCDANIELS K, DOWNS R J, MELDNER H, et al. High strength to weight ratio non-woven technical fabrics for aerospace applications[C]//18th AIAA Lighter-Than-Air Systems Technology Conference. Seattle, Washington, 2009: 2802-2817.
[5] MASAAKI N, SHOJI M, TOYOTOSHI K. Investigation of long term weathering characteristics on high strength and light weight envelope material zylon[C]//11th AIAA Aviation Technology, Integration, and Operations(ATIO) Conference. Virginia Beach, USA, 2011:6938-6945.
[6] SHOJI M, KOUICHI S, TOYOTOSHI K, et al. Tear propagation of a high performance airship envelope material[C]//7th AIAA Aviation Technology, Integration and Operations Conference. Belfast, Northern Ireland, 2007: 7829-7842.
[7] ZHAI H L, EULE A R. Material challenges for lighter-than-air systems in high altitude applications [C]//5th AIAA Aviation, Technology, Integration, and Operations Conference (ATIO). Arlington, Virginia, 2005: 7488-7501.
[8] STOCKBRIDGE C, CERUTI A, MARZOCCA P. Airship research and development in the areas of design, structures, dynamics and energy systems[J]. International Journal of Aeronautical and Space Sciences, 2012, 13(2): 170-187.
[9] KANG W G, SUH Y, WOO K, et al. Mechanical property characterization of film-fabric laminate for stratospheric airship envelope[J]. Composite Structures, 2006, 75:151-155.
[10] BAI J, XIONG J, CHENG X. Tear resistance of orthogonal Kevlar-PWF-reinforced TPU film[J]. Chinese Journal of Aeronautics, 2011, 24(1): 113-118.
[11] 刘龙斌,曹帅,吕明云.临近空间飞艇蒙皮用材料撕裂行为的数字散斑法研究[J].材料科学与工程,2014, 14(20):137-143.
[12] MINAMI H. Strength of coated fabrics with crack[J].Journal of Industrial Textiles,1978, 7(4): 269-292.
[13] CHU C Y. A study of tearing properties of membrane coated fabrics[J]. Journal of China Textile University: English Edition,1991,8(4):1-9.
[14] 马倩,王萍,王永欣.机织物撕裂破坏分析及其自身性能对二维纺织复合材料力学性能的重要性[J].纤维复合材料,2010, 15(3): 15-20.
[15] WANG SH N, SUN B Z, GU B H. Analytical modeling on mechanical responses and damage morphology of flexible woven composites under trapezoid tearing[J].Textile Research Journal, 2013, 83(12): 1297-1309.
[16] LIU L B, LÜ M Y, XIAO H D. Tear strength characteristics of laminated envelope composites based on single edge notched film experiment[J].Engineering Fracture Mechanics, 2014,127: 21-30.
[17] WANG P, SUN B, GU B. Comparisons of trapezoid tearing behaviors of uncoated and coated woven fabrics from experimental and finite element analysis[J].International Journal of Damage Mechanics, 2013, 22(4): 464-489.
[18] MAEKAWA S, SHIBASAKI K, KUROSE T, et al. Tear propagation of a high-performance airship envelope material [J]. Journal of Aircraft, 2008, 45(5): 1546-1553.
[19] BIGAUD D, SZOSTKIEWICZ C, HAMELIN P. Tearing analysis for textile reinforced soft composites under mono-axial and bi-axial tensile stresses[J]. Composite Structures, 2003, 62(2):129-137.
[20] LUO Y X, HU H, RAUL F. Precracked tearing properties of flexible composites reinforced with the biaxial warp knitted fabric under biaxial loads[J]. Industrial Textiles, 2009, 27(4):25-27.
[21] TOPPING A D. The critical slit length of pressurized coated fabric cylinders[J].Journal of Industrial Textiles, 1973, 3(2): 96-110.
[22] ENNOURI T, TOAN V K. Mechanics and mechanisms of tear resistance of woven fabrics[J]. Theoretical and Applied Fracture Mechanics, 2012, 61: 33-39.
[23] ENNOURI T, PATRICIA D, TOAN V K. Tear resistance of woven textiles-criterion and mechanisms [J]. Composites: Part B, 2011, 42:1851-1859.
[24] ZHONG W, PAN N, LUKAS D. Stochastic modelling of tear behaviour of coated fabrics[J]. Modelling and Simulation in Materials Science and Engineering, 2004, 12(3):293-309.
[25] WANG P, MA Q, SUN B Z, et al. Finite element modeling of woven fabric tearing damage[J]. Textile Research, 2011, 81:1273-1286.
[26] 汪黎明,高传平,李立.机织物撕裂破坏机理的研究[J].青岛大学学报,2001,16(1):29-32.
[27] HEINRCH G, STRUVE J,GERBER G. Mesoscopic simulation of dynamic crack propagation in rubber materials[J]. Polymer,2002,43(2):395-401.
[28] GODFREY T A, ROSSETTOS J N, BOSSELMAN S E. The onset of tearing at slits in stressed coated plain weave fabrics[J]. Journal of Applied Mechanics, 2004, 71(6): 879-886.
[29] GODFREY T A, ROSSETTOS J N. Analysis of damage tolerance to tear propagation in stressed structural fabrics [J]. Structures and Materials, 2000, 6: 149-158.
[30] Airship design criteria:FAA-P-8110-2—1995[S]. USA: Department of Transportation and Federal Aviation Administration,1995.
[31] Cloth, laminated,ZPG2 and ZPG2W type airship envelope:MIL-C-21189(1)—1959[S].USA,1959.
[32] 谭惠丰,万志敏,董亚波.Vectran织物复合材料冲击响应与失效模式分析[J].航天返回与遥感, 2010,31(6):9-15.
[33] 杜以军,蒋金华,陈南梁.Vectran 纤维复合材料抗破坏性能的研究[J].玻璃钢/复合材料,2014(2):27-32.
文章编号:1671-0444(2016)03-0323-09
收稿日期:2015-05-27
基金项目:国家自然科学基金资助项目(51278299);江苏省基础研究计划(自然科学基金)资助项目(BK20150775)
作者简介:陈建稳(1981—),男,山东菏泽人,博士,研究方向为空间结构、薄膜结构. E-mail: jianwench@yeah.net 陈务军(联系人),男,教授,E-mail:cwj@sjtu.edu.cn
中图分类号:V 274
文献标志码:A
Analytical Model on Mechanical Responses of Laminated Fabrics for Airships under Central Crack Tearing
CHENJian-wen1,CHENWu-jun2,ZHOUHan1,GAOCheng-jun2,HEShi-zan2
(1. School of Science, Nanjing University of Science and Technology, Nanjing 210094, China;2. Space Structures Research Center, Shanghai Jiao Tong University, Shanghai 200030, China)
Abstract:Central crack tearing damage is one of the main failure types for laminated fabrics during their serving life. In order to analyze the tear behaviors of laminated fabrics, a new analytical model was developed according to the plain weave structure of the studied materials. Two new concepts—equivalent yarns and narrow transitional zone of stress concentration, were introduced to simplify the parameter model and refine the distribution of stress field in the narrow transitional zone, respectively. The model, with different crack lengths in the range of 10 mm to 40 mm, was validated from the good agreement between the calculated results and the experimental results. Based on the analytical model, the tearing deformation at different narrow transitional zones had been calculated to derive the tearing resisting forces, the tearing propagation mechanism of the envelope materials was analyzed, and it was found that the failure strain and the elastic modulus of the yarn as well as the weaving density of the fabric were the key factors affecting the tearing resisting forces of the envelope materials. Investigations on the tearing mechanism of laminated fabrics will provide significant guidance for the fabric design, crack arrest, and safety assessment of airship structures.Key words: laminated fabrics; central crack tearing; tearing mechanisms; narrow transitional zone of stress concentration; equivalent yarns
