弦向角对立木圆盘无损检测中电阻的影响1)

王兴龙　王立海　　　岳小泉　　葛晓雯　刘泽旭

(东北林业大学，哈尔滨，150040)　　　　(福建农林大学)　　　　　　(东北林业大学)



弦向角对立木圆盘无损检测中电阻的影响1)

王兴龙王立海岳小泉葛晓雯刘泽旭

(东北林业大学，哈尔滨，150040)(福建农林大学)(东北林业大学)

摘要研究了电流在不同树种圆盘横截面上传导时电阻的变化情况，以期进一步认识其传导规律及影响因素，为利用电阻法进行木材缺陷检测提供理论依据。选择白桦(Betula platyphylla)、红松(Pinus koraiensis)、落叶松(Larix gmelinii)、青杨(Populus davidiana)和杉木(Cunninghamia lanceolata)5种树种的10个圆盘为试验材料，在圆盘的横截面上，测试不同弦向角下的圆盘电阻，并讨论其变化规律。结果表明：径向对称弦向角对圆盘电阻值的影响无显著性差异(P>0.05)，其它弦向角对圆盘电阻值的影响差异极其显著(P<0.01)；电流在圆盘横截面上传导时电阻值随弦向角的增大先增大后减小，径向电阻值最大。不同弦向角下圆盘电阻值拟合曲线为一条开口向下的抛物线，相关系数均高于0.9；不同树种的试样在相同弦向角下的电阻值不同，但变化趋势相同。

关键词木材无损检测；电阻法；弦向角

我国的森林资源和木材需求之间存在着巨大的结构性矛盾，而木材的利用率却偏低。进行木材无损检测研究，是提高木材利用率的重要手段[1]。目前应用到木材性质检测的无损检测技术已达几十种[2]，但是很多检测技术只能在室内对木材材质、特性和缺陷等进行检测，且研究主要局限于板材，能够在野外对活立木进行检测的仪器并不多[3-5]。应用广泛的有生长锥、阻抗仪和应力波，其中生长锥取样虽然最直观，但是对树木损伤最大，且只能检测单一方向；阻抗仪虽然降低了对树木的损伤，但也只能检测单一方向[6-8]；应力波是较为成熟的一项技术，实现了对活立木断层的检测，但在实际使用中也暴露了许多问题，比如受人为和受外界因素的影响比较大、检测耗时效率低、野外携带不方便、对轻度腐朽甚至未能显示异常、对面积较小的孔洞往往仅给出是小面积腐朽的结果等问题[9-11]。鉴于电阻法具有操作简单、工作便捷、受干扰小、对早期腐朽灵敏度高、空洞和腐朽检测图像区别明显等优点[12-14]，可将其引进，以弥补现有技术存在的不足。

利用电阻法对立木或者原木的内部缺陷进行无损检测，主要是通过分析电流在其横截面上传导时电阻的变化，进而对其健康情况进行评估。国外已经采用电阻法对活立木内部缺陷检测进行了一系列研究，从针式探测法、四点测试法到电阻层析成像技术，实现了点、线、面的应用研究[15-17]。国内也已采用电阻法进行木材缺陷检测，并从初期仅研究木材的直流电、交流电基本特性，发展到探讨木材解剖分子和化学结构等构造因子和含水率、温度、频率、纹理等因子对木材电学性质参数的影响机制，以及介电弛豫的分子论等[18-21]；但研究对象一直局限于小试件和单个影响因子分析，没有对立木或原木的内部缺陷检测进行研究。因此，有必要以圆盘为研究对象，研究电流在其横截面上传导时弦向角对电阻的影响。笔者在实验室内针对杉木等圆盘试样，测量激励信号以不同弦向角在圆盘横截面上传导时的电阻值，研究弦向角对电阻值的影响，分析原木径向和弦向的电学性质差异，以期进一步认识电流在圆盘横截面的传导规律及其影响因素，为利用电阻法进行木材缺陷无损检测提供理论依据。

1材料与方法

1.1材料

杉木(Cunninghamia lanceolata)试样取自福建省长汀县楼子坝林场，白桦(Betula platyphylla)、红松(Pinus koraiensis)、落叶松(Larix gmelinii)、青杨(Populus davidiana)试样取自松花江中游南岸的黑龙江省方正林业局。立木样本被伐倒后，立即制成原木；然后再将原木锯切加工成圆盘，圆盘试样均无节子、腐朽和开裂，直径为20～35cm，厚度5cm，心材与边材的比例为24%～68%。各树种圆盘均为2个，依次标记为S1(1号杉木圆盘)、S2(2号杉木圆盘)、B3(3号白桦圆盘)、B4(4号白桦圆盘)、H5(5号红松圆盘)、H6(6号红松圆盘)、L7(7号落叶松圆盘)、L8(8号落叶松圆盘)、Q9(9号青杨圆盘)、Q10(10号青杨圆盘)。其中杉木是主要实验树种，用于弦向角的分析，其它树种用来做对比分析。为减少样本含水率变化，在运输过程中，采用密封袋把样本包好，运回实验室后立即测试，实验室内环境温度25 ℃，空气相对湿度56%。

1.2仪器

激励信号源来自深圳驿生胜利科技有限公司生产的VC2002函数信号发生器，使用北京普源精电科技有限公司生产的DS1025型示波器对激励信号进行监控和校准；用深圳鸿昌滨江电子仪器有限公司生产的DT9206型数字式万用表测量试件的负载电压，另外使用10kΩ的定值电阻；含水率的测量仪器是上海佳实电子科技有限公司生产的FD-100B型高周波木材水分仪；用钢卷尺测量圆盘周长及弦长。

1.3方法

1.3.1含水率和弦长的测定

首先，在生长轮方向上，使用高周波数字水分仪分别对心材和边材的含水率进行重复测量，并计算其平均值，精确至0.1%[22]；然后，在圆盘中间横截面四周随机选取一点，布置钉子将该点标记为1号点，再在与1号位置以弦向角(θ)每隔7.5°的方式布置一个钉子(见图1)，逆时针依次标记为2、3、4、…、24号点，这些点即为电阻试验测试点。用钢卷尺测量所有点任意两点的弦长。弦向角是指在圆盘横截面上，以圆周上某一点为切点，通过这一切点的弦向线与切线之间的夹角[23-24]。在本试验中，弦向角实指激励信号两电极之间的连线与以负极位置为切点的切线之间的夹角。角度等于两电极连线对应的圆心角的一半，和为180°的两个弦向角称为关于径向对称的弦向角；反之，称为其它弦向角。

图1　激励电极在圆盘端面的弦向分布

图2　试验电路图

1.3.2测量组数量的确定

如果绕圆盘四周布置的测试点数为奇数，将无法测得弦向角为90°的径向电阻，所以选择偶数测试点绕圆盘四周进行布置；测试点数量越多，则圆盘周长划分得越精细，故选择24个测试点进行24组数据测量，并将相同弦向角下的电阻值求取平均值以减小圆盘截面形状不规则对电阻值的影响。

1.3.3电阻值的测定

本研究在进行圆盘电阻测量时，观察的重点是圆盘电阻的变化趋势，而不是电阻值本身，对精度的要求有限；试验数量也比较大，单次测量电阻的时间不宜太长，故相对于电桥法，伏安法更适于本研究中的圆盘电阻测量。根据以往研究经验，选用1 000Hz、3V的正弦波作为激励信号[25]。试验电路如图2所示，一方面为减小温度的影响，另一方面为求出电路电流，试验时圆盘试件先与10kΩ的定值电阻(RR)串联，再与交流电源相连，在定值电阻和圆盘试样两端各用一个万用电表测量负载电压以计算圆盘试样的电阻值。具体试验步骤为：①1号测试点接电源一端，2—24号测试点依次接电源另一端，读出每次圆盘试样两端万用电表1的示数，记为UD；定值电阻两端万用电表2的读数记为UR，1号测试点测量结束。②2号测试点接电源一端，1、3—24号测试点依次接电源另一端，记录UD和UR，2号测试点测量结束。③以此类推，完成3—24号测试点的测量，至此结束对一个圆盘试件的测量。这样24个测试点可获得552个独立的测量值。圆盘的电阻值(RD)可用如下公式计算：

RD=UD/ID=UD/IR=UD/(UR/RR)=(UDRR)/UR。

表1圆盘S1每个测量点电阻值与弦向角之间的一元二次回归模型

测量点y=A+Bθ+Cθ2FR21y=15.243+1.573θ-0.008θ2321.7790.9702y=17.642+1.456θ-0.008θ2197.2810.9523y=17.261+1.477θ-0.008θ2224.7360.9574y=17.706+1.452θ-0.008θ2210.0200.9555y=17.440+1.552θ-0.008θ2240.6930.9606y=15.561+1.525θ-0.008θ2469.1540.9797y=16.939+1.536θ-0.008θ2476.2490.9798y=6.146+1.570θ-0.008θ2919.2190.9899y=6.723+1.544θ-0.008θ2854.9780.98810y=9.077+1.497θ-0.008θ2973.1790.99011y=14.965+1.449θ-0.008θ2817.7970.98812y=12.004+1.380θ-0.008θ2651.3550.98513y=17.074+1.263θ-0.007θ2781.4100.98714y=23.137+1.178θ-0.007θ2705.6470.98615y=29.946+1.079θ-0.006θ2522.9380.98116y=29.118+1.005θ-0.006θ2178.8200.94717y=25.209+0.924θ-0.005θ2154.6570.93918y=23.232+0.867θ-0.005θ2177.2980.94719y=20.985+0.894θ-0.005θ294.6550.90420y=12.684+1.041θ-0.005θ2139.5600.93321y=13.831+0.999θ-0.005θ2130.5180.92922y=14.284+0.958θ-0.005θ2153.3430.93923y=13.749+0.941θ-0.005θ2191.1250.95024y=11.565+0.952θ-0.005θ2243.0520.960

2结果与分析

2.1弦长随弦向角的变化

图3显示的是圆盘S1各测量点的弦向角与激励信号两极间距离的关系，即各测量点不同弦向角下的弦长、电流信号在杉木内部传导的直线距离，图形呈现出随着弦向角的增大传导距离先增大后减小的趋势。进一步采用二次多项式拟合，以弦向角(θ)为自变量，传导距离(d)为因变量，建立各测试点θ与d的拟合方程。拟合方程的相关系数R2=0.99，拟合效果非常好，表明试样的圆周上没有大的凸起或者凹陷变化，圆周比较平滑且测试点分布比较均匀。因此可以认为单个试样的24组数据中剩余的23组数据也都是每隔7.5°测量得到的。

2.2激励电压随弦向角的变化

图4显示的是测量圆盘S1不同弦向角下激励电压的实际输出值，采用二次多项式拟合，以θ为自变量，电压(U)为因变量，建立每个测试点下θ与U的拟合方程。可知，虽然多项式拟合也大致呈现了激励电压随着弦向角的增大先增大后减小的趋势，但是相关系数R2=0.7，表示拟合效果一般，并且回归系数均接近于0。弦向角很小和弦向角很大时电压变化较大，中间大部分都变化不显著，电压幅值大多在1.89～1.9V。24组数据的方差分析表明，弦向角对电压输出值的影响非常不显著(P=0.999)，即不同弦向角间电压的实际输出值并无显著差异。鲍震宇曾对山杨木材电阻测量的研究发现，2～16V交流信号激励下的电阻值几乎不随着电压的变化而变化[25]。可知，激励电压的变化对电阻测量的影响不显著，即本实验激励电压的差异不会引起电阻值的较大差异。

图3　圆盘S1各测试点不同弦向角下的弦长变化曲线

图4　圆盘S1不同弦向角下的激励电压实际输出值

2.3弦向角对立木圆盘电阻的影响

2.3.1对杉木圆盘电阻的影响

图5显示的是不同弦向角下杉木圆盘电阻值变化趋势，该图由12条折线组成(原图有24条折线，为便于显示选取其中12条)，每条折线上有23个电阻值，分别代表了每个测量点23个不同弦向角下的电阻值变化趋势。可知：随着弦向角的增大电阻呈先增大后减小的趋势，且最大值出现在90°附近；方向角相同电阻不相同时，它会在一定范围内波动，但电阻总的变化趋势是一样的。径向对称的弦向角对电阻值影响的单因素方差分析表明，它对电阻值的影响不显著(P=0.995)。径向非对称的弦向角对电阻值影响的单因素方差分析表明，它对电阻值的影响极显著(P<0.01)。将24个测量点的每个弦向角与电阻值进行拟合(见表1)，回归系数均在一定范围内波动。这种差异是由木材构造的各向异性导致的，因此为解决单个检测点的电阻模型随机性较大的问题，提高模型的拟合优度，减小单个点检测时电阻误差，取平均电阻值作为实验分析的数据，从而控制实验误差。可知，随着弦向角的增大平均电阻值呈现先增大后减小的趋势，整体上呈显著的二次函数关系，拟合方程为y=-0.006 9θ2+1.254 6θ+16.73，相关系数R2=0.99(P<0.01)，说明拟合效果很好。θ<90°时，平均电阻值随着弦向角的增大逐渐增大；θ=90°时，电流通过圆盘横截面直径时平均电阻值达到最大；θ>90°时，平均电阻值随着弦向角的增大逐渐的减小。进一步建立θ对Rθ/R90的回归模型Rθ/R90=-0.000 1θ2+0.017 2θ+0.236 8，相关系数R2=0.99(P<0.01)。其中：Rθ为沿弦向角θ的电阻值；R90为径向电阻值，即弦向角θ为90°时的电阻值。模型更具普遍性。

这是因为木材是各向异性的非均匀介质材料，在圆盘的横截面上，木材的密度、含水率、生长轮宽度、早晚材比率和木射线组织比率等影响电流在圆盘横截面上传导的因子随着弦向角的变化而变化。弦向角对圆盘电阻值的影响原因有3点。其一，当弦向角较小时，激励信号的两极距离较近，电势在激励电极处取得最大值后，在激励电极周围迅速降低接近为零，电流密度集中于此；而这样对远离激励电极的区域来说，电流很少流过。所以此时电流流经圆盘横截面区域较小，产生的电阻也就较小。当弦向角较大时，电势同样在两个激励电极处取得最大值；但是沿着圆盘中心位置逐渐降低，电流密度随着与激励电极的距离增大呈由快到慢的非线性下降趋势。从激励点出发，要形成通路，电流流经激励电极之间的区域圆盘横截面区域变大，产生的电阻也就较大[26-30]。其二，木材的密度沿着髓心向外呈直线或者曲线减小，密度小的木材比密度大的具有稍微高的电阻率；而木材密度对电阻率的影响与含水率对电阻率的影响相比是没有意义的，随着含水率的增加电阻逐渐减小。本试验圆盘试件的边材含水率均高于心材含水率，弦向角较小时电流主要流经圆盘边材，边材含水率较高，电阻较小。随着弦向角增大，电流流经圆盘路径的含水率逐渐减小，电阻相应增大。其三，如果将激励电极两点间的电阻抽象为两点之间所有连线电阻的并联电阻，根据并联后的等效电阻小于并联的最小电阻，则两点弦长上的电阻最能代表所对应弦向角的电阻。随着弦向角的增加，激励电极之间的弦长逐渐增大(见图3)，弦长上的电阻也就不断累加，弦向电阻值也相应地变大。将图6中各个弦向角的平均电阻值与图3对应的弦长相除，得到各弦向角下的平均电阻率。电阻率随着弦向角的增大先减小后增大，弦向电阻率大于径向电阻率，这与李坚、白同仁等人的研究结果是一致的[31]，从而也证明了本研究建立的平均电阻与弦向角之间的拟合模型是有效的。

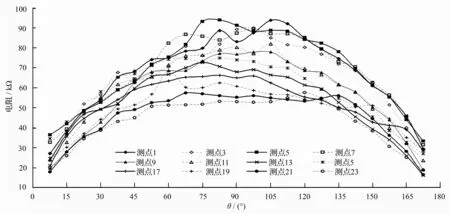
图5　不同测量点下的圆盘S1电阻值变化曲线

2.3.2对其它树种立木圆盘电阻的影响

图7a显示的是S1号杉木和S2号杉木样品在各个相同弦向角下电阻值之间的关系。回归分析表明，两者之间的线性关系极为显著(R2=0.998 1)；随着弦向角的变化，横截面积不同的同种树种也会有着相同的电阻变化规律，弦向角对圆盘电阻的影响不受圆盘横截面面积的影响。同理对其它相同树种不同截面面积的样品进行分析，结果也是线性关系极其显著。图7b—图7e依次显示的是S1号杉木与B3号桦木、H5红松、L7落叶松、Q9青杨样品在各相同弦向角下电阻值之间的关系。从回归结果来看，不同树种在相同方向角的电阻值不同，但变化规律基本相同。弦向角对圆盘电阻的影响规律不受树种的影响，结合2.3.1的结论可知，随着弦向角的增大，不同活立木圆盘电阻均呈现先增大后减小的趋势，径向电阻最大，整体趋势为一条开口向下的抛物线。

图6　不同弦向角下的圆盘S1平均电阻和平均电阻率变化曲线

图7　不同立木圆盘相同弦向角下的电阻值关系

3结论

径向对称的弦向角对电阻值影响不显著，其它弦向角对电阻值影响显著，且随着弦向角的增加，电流在杉木等树种圆盘横截面上传导时电阻值均呈曲线趋势，先增加后减小。所建立的电流在杉木圆盘横截面上传导时电阻值与弦向角间的二次多项式拟合模型拟合效果比较好。拟合曲线呈现类似开头向下的近抛物线形式，相关系数均在0.9以上；当弦向角为90°时，电流在杉木圆盘横截面上传导时电阻值达到最大值。不同横截面面积和不同树种的试样在相同弦向角下的电阻值大小不同，但变化趋势均相同。

其它树种圆盘横截面上弦向角对电流传导时电阻的影响：弦向角对电流传导时的电阻有一定影响，不同树种的影响程度不同，但是趋势相同。因此，利用电阻法进行木材缺陷检测时需要考虑弦向角对电阻的影响，比如传导路径的延长和弦向角的改变都是空洞缺陷电阻增大的原因。本研究结果可为通过电阻差异及规律，对原木分级、立木健康检测等提供理论依据。

参考文献

[1]王立海，杨学春，徐凯宏.木材无损检测技术的研究现状与进展[J].森林工程，2001，17(6)：1-3.

[2]王欣，申世杰.木材无损检测研究概况与发展趋势[J].北京林业大学学报，2009，31(S1)：202-205.

[3]余观夏，张爱珍，史伯章，等.用应力波频谱分析技术检测原木中的腐朽[J].东北林业大学学报，2007，35(10)：22-25.

[4]安源，殷亚方，姜笑梅，等.应力波和阻抗仪技术勘查木结构立柱腐朽分布[J].建筑材料学报，2008，11(4)：457-463.

[5]杨慧敏，王立海.立木与原木内部腐朽二维成像检测技术研究进展[J].林业科学，2010，46(7)：170-175.

[6]吴福社，吴贻军，邵卓平.应力波仪和阻力仪用于雪松立木内部材性检测的研究[J].安徽农业大学学报，2011，38(1)：127-130.

[7]刘泽旭，王立海，鲍震宇，等.红松活立木内部腐朽程度的定量检测[J].东北林业大学学报，2015，43(6)：89-92，106.

[8]孙天用，王立海，侯捷建，等.木材含水率和地形条件对红松活立木腐朽程度的影响[J].应用生态学报，2015，26(2)：349-355.

[9]梁善庆，王喜平，蔡智勇，等.弹性波层析成像技术检测活立木腐朽[J].林业科学，2008，44(5)：109-114.

[10]刘光林.树木内部应力波传播速度模型研究[D].临安：浙江农林大学，2014.

[11]刘丰禄，张厚江，姜芳，等.人工林活立木材质应力波无损检测研究进展[J].林业机械与木工设备，2015，43(3)：8-12.

[12]OLIVAJ,ROMERALOC,STENLIDJ.AccuracyoftheRotfinderinstrumentindetectingdecayonNorwayspruce(Picea abies)trees[J].ForestEcologyandManagement,2011,262(8):1378-1386.

[13]鲍震宇，王立海.电阻测试法在立木腐朽检测中的应用研究进展[J].森林工程，2013，29(6)：47-51.

[14]王兴龙，王立海.电极数量对ERT技术检测原木缺陷效果的影响[J].林业科技开发，2015，29(6)：99-103.

[15]SHIGOAL,SHIGOA.Detectionofdiskcolorationanddecayinlivingtreesandutilitypoles[J].ForestServiceoftheUSDepartmentofAgriculture，1974,29(4):3-10.

[16]ROMERALOC.ReliabilityofRotfinderinstrumentfordetectingdecayinstandingtrees[D].Uppsala:SwedishUniversityofAgriculturalScience,2010.

[17]MartinT.Complexresistivitymeasurementsonoak[J].EuropeanJournalofWoodandWoodProducts,2012,70(1/2/3):45-53.

[18]顾锡爵，周曼.微波频率下木材介电常数和损耗的测量[J].南京林业大学学报，1987，11(3)：95-99.

[19]殷祥源.木材真实电阻的测量[J].南京林业大学学报，1988，12(1)：91-95.

[20]池玉杰.木材腐朽与木材腐朽菌[M].北京：科学出版社,2002.

[21]李坚.木材科学[M].北京：高等教育出版社,2002.

[22]徐华东，王立海.温度和含水率对红松木材中应力波传播速度的影响[J].林业科学，2011，47(9)：123-128.

[23]王立海，王洋，徐华东.弦向角对应力波在原木横截面传播速度的影响[J].林业科学，2011，47(8)：139-142.

[24]刘光林，李光辉，孙晔，等.树木内部应力波传播速度模型[J].浙江农林大学学报，2015，32(1)：18-24.

[25]鲍震宇，王立海.激励信号对山杨木材电阻测量的影响[J].林业科技开发，2015，29(1)：79-82.

[26]邹璐.电阻层析成像系统仿真建模研究[D].北京：清华大学，2002.

[27]余金华.电阻层析成像技术应用研究[D].杭州：浙江大学，2005.

[28]燕增伟.32电极电阻层析成像系统仿真研究[D].北京：北京交通大学，2009.

[29]张彦俊，陈宇，陈德运，等.电阻层析成像系统敏感场特性分析及图像重建[J].计算机科学，2010，37(8):257-261.

[30]王湃.电阻层析成像(ERT)技术及其在两相流检测中的应用[D].西安：西安电子科技大学，2013.

[31]白同仁，陈森，曾其蕴.马尾松木材介电性质的测试[J].木材工业，1987，1(4)：1-5.

第一作者简介：王兴龙，男，1992年1月生，东北林业大学工程技术学院，硕士研究生。E-mail：823390979@qq.com。 通信作者：王立海，东北林业大学工程技术学院，教授。E-mail：wanglihai2012@126.com。

收稿日期：2016年1月20日。

分类号S781.51

EffectsofTangentialAnglesonElectricalResistanceofStandingTreeDisk//

WangXinglong,WangLihai

(NortheastForestryUniversity,Harbin150040,P.R.China);YueXiaoquan(FujianAgricultureandForestryUniversity);GeXiaowen,LiuZexu(NortheastForestryUniversity)//JournalofNortheastForestryUniversity，2016,44(8)：78-82，107.

Weselecteddifferentspeciesassamplestostudytheresistancesandthoseinfluencesfactorsindisk’scrosssectionandimprovethetheoreticalbasisofelectricalresistancetestingmethodinwoodnon-destructivetesting.DisksofBetula platyphylla SukaczevandCunninghamia lanceolatawerechosenastestmaterialstomeasuretheresistancesofdiskatdifferenttangentialangles.Theresistancesofdiskwerenotsignificantlyaffectedbytangentialangleofradicalsymmetric.Othersweresignificantaffectedbytangentialangles.Inthecrosssectionofdisk,theresistanceofdiskwasincreasedwiththeincreasingoftangentialanglebefore90°,andtheresistanceofdiskalongtheradialdirectionwasthemaximum.Whenradialdirectionanglewasincreasedgradually,thestresswavevelocitywouldbecomesmaller.Forthesamedirectionangle,theresistanceofdiskwasdifferentindifferentspecies.

KeywordsWood non-destructive testing; Electrical resistance test; Tangential angle

1)国家林业局“948”项目(2014-4-78)。

责任编辑：戴芳天。