模糊集的直觉熵与直觉相似度

石 乙 英，　袁 学 海

( 1.大连理工大学 控制科学与工程学院, 辽宁 大连　116024；2.沈阳理工大学 理学院, 辽宁 沈阳　110159；3.大连理工大学盘锦校区 基础教学部, 辽宁 盘锦　124221 )



模糊集的直觉熵与直觉相似度

石 乙 英1,2，袁 学 海*1,3

( 1.大连理工大学 控制科学与工程学院, 辽宁 大连116024；2.沈阳理工大学 理学院, 辽宁 沈阳110159；3.大连理工大学盘锦校区 基础教学部, 辽宁 盘锦124221 )

摘要：熵与相似度都是用来描述模糊集模糊程度的指标，现有方法都是通过将其刻画为具体的数值展开研究．针对当模糊集的模糊程度具有不确定性，无法利用具体的数值表示时，如何利用熵与相似度来进行度量的问题展开讨论．首先提出了直觉熵与直觉相似度的定义，其次利用两个定理说明直觉熵与直觉相似度可以相互转化．

关键词：熵；相似度；直觉熵；直觉相似度

0引言

熵在信息论中是用来衡量不确定程度的指标，近年来在决策问题中得到了广泛的应用[1-5]．Xu等[4]通过熵和犹豫模糊集的Cross-熵，研究了两种属性值为犹豫模糊集的多属性决策方法．Jin等[5]建立了最小熵最优权准则的规划模型，并给出了基于加权和评分函数的区间值直觉模糊多准则群决策的具体方法．而相似度也是描述模糊集模糊程度的指标，对于其与熵的关系，Wei等[6]展开了相关的研究．

在上述研究中，通常将模糊集的模糊程度描述为某个具体的数值，显然无法同时表述肯定和否定的含义．而由于认识的复杂性，人们对事物认知的表述往往具有不确定性．例如当模糊集的模糊程度描述为“肯定为0.1，否定为0.5”时，如何利用熵与相似度来表示是一个值得探讨的问题．本文分别以模糊集的熵和相似度的概念为基础，提出直觉熵和直觉相似度的概念并构建出相应的表达式，对二者的关系展开讨论．

1模糊集的直觉熵

本文基于模糊集的熵来定义直觉熵以及构造具体的表达式．

设X为论域，称映射μA：X→[0，1]为X的一个模糊子集，μA(x)为x对A的隶属度，记F(X) 为X上所有模糊子集组成的集合，P(X)为X上所有经典子集组成的集合．

定义1[7]X为非空集合，若映射μA：X→[0，1]，νA：X→[0，1]满足

μA(x)+νA(x)≤1；∀x∈X

则称A=(X，μA，νA)为X上的直觉模糊集，记为A(x)=(μA(x)，νA(x))，其中μA(x)、νA(x)分别表示X中元素x对集合A的隶属度和非隶属度．X中直觉模糊集的全体记为IF(X)．

令L={(a，b)|a，b∈[0，1]，a+b≤1}，则直觉模糊集A=(X，μA，νA)可以视为L-模糊集：

A：X→L，x

(μA(x)，νA(x))

为了方便起见，用LX={A∣A：X→L}来表示IF(X)．

1972年，De Luca和Termini给出了关于模糊集的模糊程度的公理性描述以及模糊集熵的定义．

定义2[8]如果E：F(X)→[0，1]，A

→

E(A) 满足以下性质：

(E1)若A∈P(X)，则E(A)=0；

(E4)E(A)=E(Ac)

则称E为模糊集F(X)上的熵．

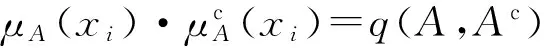
事实上，模糊集的熵通过建立一个从F(X)到[0，1]的映射来描述其模糊程度，利用对论域X上每个元素隶属度来进行计算，得到介于[0，1]的一个数值．这实质上等同于模糊集的去模糊化过程．其不足之处在于一方面会造成部分可用信息的丢失，使得结果具有不完整性；另一方面，由于人们在对事物的认知过程中往往会表现出很大程度的不确定性，这就使得对于模糊集模糊程度的表述也有不确定性．例如设U={1，2，3，4，5}，若表示“靠近3”的模糊集，其隶属度函数可以表示为A={(1，0)，(2，0.6)，(3，1)，(4，0.6)，(5，0)}．也可以表示为B={(1，0)，(2，0.7)，(3，1)，(4，0.7)，(5，0)}，且有E(A)=0.384，E(B)=0.336．这是由于对于模糊集模糊程度的认知存在不确定性，导致对模糊集的描述方式不同，得到的熵也不同．因此一个数值很难准确地描述这种性质．这就需要将熵的取值从具体的数值推广至能同时表示肯定及否定的量．基于此，提出模糊集直觉熵的定义如下．

定义3 若ITE：F(X)→L满足：

(EP1)若A∈P(X)，则ITE(A)=(0，1)；

(EP4)ITE(A)=ITE(Ac)

则称ITE为模糊集上的直觉熵．

注 由L的运算可知，若ITE(A1)=(a1，b1)，ITE(A2)=(a2，b2)，则有

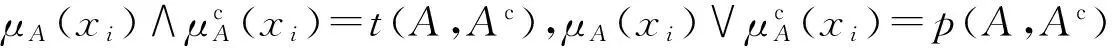
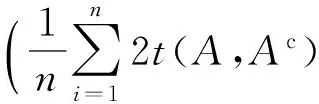
(1)

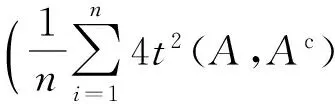
(2)

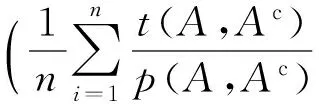
(3)

定理1ITEi(A)(i=1，2，3)为直觉熵．

证明 以i=3为例，首先证ITE3(A)∈L．

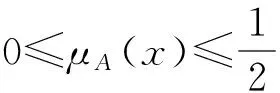
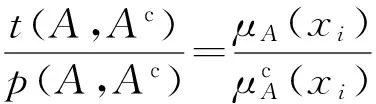
则有

即ITE3(A)∈L．

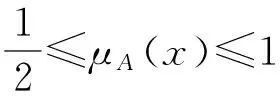
(EP1)若A∈P(X)，则μA(x)=0或μA(x)=1，即

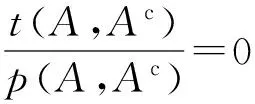
也就是说ITE3(A)=(0，1)．

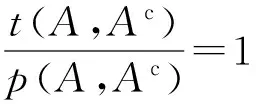
也就是说ITE3(A)=(1，0)．

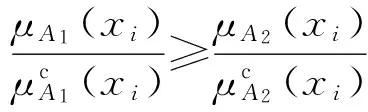
即ITE3(A2)≤ITE3(A1)．

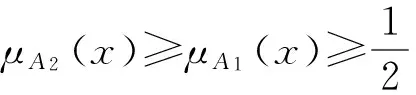
(EP4)ITE3(A)=ITE3(Ac)显然得证．

其他情形同理可得．

□

2模糊集的直觉相似度

相似度也是用来描述模糊集模糊程度的指标．为了度量两个模糊概念的相似程度，在1987年，Pappis和Karacapilidis给出了关于两个模糊集相似度定义的公理性描述．

定义4[9]若S：F(X)×F(X)→[0，1]满足：

(S1)若A∈P(X)，则有S(A，Ac)=0；

(S2)S(A，A)=1；

(S3)S(A，B)=S(B，A)；

(S4)∀A，B，C∈F(X)，若A⊆B⊆C，则

S(A，C)≤S(A，B)，S(A，C)≤S(B，C)

称S(A，B)为模糊集A、B的相似度．

例如，若论域X={x1，x2，…，xn}，A、B为X上的模糊集，令μA(xi)-μB(xi)=g(A，B)，则

为模糊集A、B的相似度．

事实上，模糊集的相似度是利用论域X上两个模糊集元素隶属度来确定[0，1]间的一个数值．同样由于认知过程中的不确定性，需要将相似度的概念推广至直觉相似度：

定义5 若ITS：F(X)×F(X)→L满足以下性质：

(SP1)若A∈P(X)，则ITS(A，Ac)=(0，1)；

(SP2)ITS(A，A)=(1，0)；

(SP3)ITS(A，B)=ITS(B，A)；

(SP4)∀A，B，C∈F(X)，若A⊆B⊆C，则ITS(A，C)≤ITS(A，B)，ITS(A，C)≤ITS(B，C)称ITS(A，B)为A、B的直觉相似度．

例如，令X={x1，x2，…，xn}，μA(xi)+μB(xi)=h(A，B)，定义

(4)

(5)

定理2ITSi(A，B)(i=1，2)为直觉相似度．

证明 以i=2为例，首先证ITS2(A)∈L．当μA(x)≤μB(x)时，有

即ITS2(A)∈L．

当μA(x)≥μB(x)时，同理可得．

(SP1)若A∈P(X)，则μA(x)=0或μA(x)=1，有

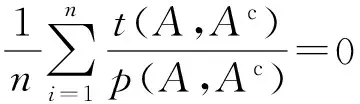
即ITS2(A，Ac)=(0，1)．

(SP2)显然有ITS2(A，A)=(1，0)．

(SP3)ITS2(A，B)=ITS2(B，A)显然得证．

(SP4)若A⊆B⊆C，则有μA(x)≤μB(x)≤μC(x)．

由式(5)可得

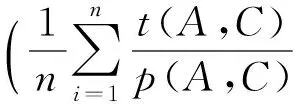
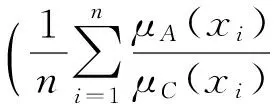
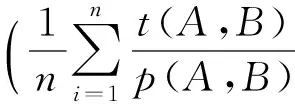
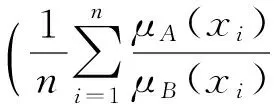
由于

即ITS2(A，C)≤ITS2(A，B)．

同理可得ITS2(A，C)≤ITS2(B，C)．

其他情形同理可得．

□

3直觉熵与直觉相似度的关系

直觉熵与直觉相似度都是描述模糊集模糊程度的指标，二者之间的关系在本文中进行讨论．

定理3 设ITE为模糊集的直觉熵，对于∀A，B∈F(X)，∀x∈X，构造函数如下：

则ITE(fi(A，B))(i=1，2，3)为模糊集A、B的直觉相似度．

证明 以i=1为例，

(SP1)若A∈P(X)，则∀x∈X，有

f1(A，Ac)∈P(X)，即ITE(f1(A，Ac))=(0，1)；

(SP2)∀x∈X，有

则ITE(f1(A，A))=(1，0)；

(SP3)显然ITE(f1(A，B))=ITE(f1(B，A))；

(SP4)若A⊆B⊆C，则μA(x)≤μB(x)≤μC(x)，即

也就是说

i=2，3类似可得．

□

根据以上定理可知，给定一个模糊集的直觉熵，可以得到相应的直觉相似度．

定理4 若ITS为模糊集的直觉相似度，则ITS(A，Ac)为模糊集A的直觉熵．

证明 (EP1)若A∈P(X)，则ITS(A，Ac)=(0，1)；

即

也就是说

(EP4)显然有ITS(A，Ac)=ITS(Ac，A)．

□

综上模糊集的直觉熵、直觉相似度二者之间等价，可以相互转化．

4结语

本文主要解决的是当考虑模糊集的模糊程度具有不确定性时，如何利用熵与相似度来进行刻画的问题．首先基于模糊集熵与相似度的定义，将其取值范围进行推广，提出了直觉熵、直觉相似度的定义以及具体的构建方法．然后对二者的关系展开了讨论．由于熵在模糊多属性决策问题中被用来确定指标集的权重，直觉熵与直觉相似度如何在模糊多属性决策问题中进行应用是今后值得研究的问题．

参考文献：

[1] 陈 雷,王延章. 基于熵权系数与TOPSIS集成评价决策方法的研究[J]. 控制与决策, 2003, 18(4):456-459.

CHEN Lei, WANG Yan-zhang. Research on TOPSIS integrated evaluation and decision method based on entropy coefficient [J]. Control and Decision, 2003, 18(4):456-459. (in Chinese)

[2]刘 智,端木京顺,王 强,等. 基于熵权多目标决策的方案评估方法研究[J]. 数学的实践与认识, 2005, 35(10):114-119.

LIU Zhi, DUANMU Jing-shun, WANG Qiang,etal. An evaluation method of scheme based on entropy weight multi-objection decision-making [J]. Mathematics in Practice and Theory, 2005, 35(10):114-119. (in Chinese)

[3]周荣喜,刘善存,邱菀华. 熵在决策分析中的应用综述[J]. 控制与决策, 2008, 23(4):361-366, 371.

ZHOU Rong-xi, LIU Shan-cun, QIU Wan-hua. Survey of applications of entropy in decision analysis [J]. Control and Decision, 2008, 23(4):361-366, 371. (in Chinese)

[4]XU Ze-shui, XIA Mei-mei. Hesitant fuzzy entropy and cross-entropy and their use in multiattribute decision-making [J]. International Journal of Intelligent Systems, 2012, 27(9):799-822.

[5]JIN Fei-fei, PEI Li-dan, CHEN Hua-you,etal. Interval-valued intuitionistic fuzzy continuous weighted entropy and its application to multi-criteria fuzzy group decision making [J]. Knowledge-Based Systems, 2014, 59(3):132-141.

[6]WEI Cui-ping, WANG Pei, ZHANG Yu-zhong. Entropy, similarity measure of interval-valued intuitionistic fuzzy sets and their applications [J]. Information Sciences, 2011, 181(19):4273-4286.

[7]袁学海,李洪兴,孙凯彪. 直觉模糊集和区间值模糊集的截集、分解定理和表现定理[J]. 中国科学F辑:信息科学, 2009, 39(9):933-945.

YUAN Xue-hai, LI Hong-xing, SUN Kai-biao. The cut sets, decomposition theorems and representation theorems on intuitionistic fuzzy sets and interval valued fuzzy sets [J]. Science in China Series F:Information Sciences, 2009, 39(9):933-945. (in Chinese)

[8]De Luca A, Termini S. A definition of a non-probabilistic entropy in the setting of fuzzy sets theory [J]. Information and Control, 1972, 20(4):301-312.

[9]Pappis C P, Karacapilidis N I. A comparative assessment of measures of similarity of fuzzy values [J]. Fuzzy Sets and Systems, 1993, 56(2):171-174.

文章编号：1000-8608(2016)04-0427-05

收稿日期：2015-12-02；修回日期: 2016-05-10．

基金项目:国家自然科学基金资助项目(61473327).

作者简介:石乙英(1980-)，女，博士生，E-mail:shiyiying98@163.com；袁学海*(1960-)，男，教授，博士生导师，E-mail:yuanxh@dlut.edu.cn.

中图分类号：O159

文献标识码：A

doi:10.7511/dllgxb201604015

Intuitionistic entropy and intuitionistic similarity of fuzzy sets

SHIYi-ying1,2,YUANXue-hai*1,3

( 1.School of Control Science and Engineering, Dalian University of Technology, Dalian 116024, China；2.School of Science, Shenyang Ligong University, Shenyang 110159, China；3.School of Science, Dalian University of Technology at Panjin, Panjin 124221, China )

Abstract：Both entropy and similarity are used to describe the fuzziness of the fuzzy sets. But in existing methods, they are still represented as specific values to be studied. Aiming at the uncertainty of the fuzziness of the fuzzy sets which can not be expressed by specific value, the problem of how to measure with entropy and similarity is discussed. Firstly, intuitionistic entropy and intuitionistic similarity are defined. And then, two theorems are proposed to show how these definitions can be deduced to each other.

Key words：entropy; similarity; intuitionistic entropy; intuitionistic similarity