一类DGH方程的新保结构算法研究

王 俊 杰

( 1.普洱学院 数学系, 云南 普洱　665000；2.西北大学 数学学院, 陕西 西安　710127 )



一类DGH方程的新保结构算法研究

王 俊 杰*1,2

( 1.普洱学院 数学系, 云南 普洱665000；2.西北大学 数学学院, 陕西 西安710127 )

摘要：DGH方程作为一类重要的非线性水波方程有着广泛的应用前景．基于哈密顿系统的多辛理论研究了一类DGH方程的数值解法，利用平均向量场方法对此哈密顿系统进行了数值离散，构造了DGH方程的局部能量保结构算法和局部动量保结构算法．数值算例表明，这两种保结构算法具有较好的长时间数值稳定性．

关键词：哈密顿系统；保结构算法；多辛理论；DGH方程

0引言

非线性水波方程是一类重要的非线性问题，随着科技的发展，非线性问题的研究已经成为当代研究的热点．非线性水波方程采用不同近似方法可以得到不同的完全可积的方程，例如KdV方程、BBM方程、Camassa-Holm方程、DGH方程．

近几十年，KdV方程、Camassa-Holm方程、DGH方程引起了国内外学者的广泛关注[1-13]，发现了这些方程的许多性质，例如：KdV方程、Camassa-Holm 方程、DGH方程都是可积方程，都广泛地存在孤立波解．Camassa-Holm方程具有一个Lax对、双哈密顿结构及无穷个守恒量．对DGH方程的研究主要集中在定性方面的研究，数值模拟研究还比较少，然而在实际应用中要求得DGH方程的精确解几乎不可能，大部分情况下只能用数值方法来模拟DGH方程，鉴于此，本文主要研究DGH方程的数值模拟方法．

现在，越来越多的学者在构造数值方法时，关注设计的算法能否保持系统原有的一些特性，这样的算法称为保结构算法．1984年我国计算数学大师冯康系统地提出了保结构算法的理论框架，随后，保结构算法迅速发展，得到了许多方程的保结构算法，这些结果无一例外地证实保结构算法有明显的优点．20世纪末，Marsden等应用变分的思想提出了偏微分方程的多辛哈密顿系统[14]，并且得到了多辛守恒律；而Reich应用辛几何的思想，提出了偏微分方程的多辛格式[15]，从而可以更加方便地应用于偏微分方程．经过十几年的发展，保多辛结构算法已经取得一定研究成果[16-27]，这些成果证明保多辛结构算法可以进行长时间的数值跟踪．

近年来，Celledoni等[28]利用AVF(平均向量场)方法来求解哈密顿系统，Chen等[29]利用AVF方法提出了多辛哈密顿偏微分方程组整体能量守恒的数值格式，Gong等[19]提出了多辛哈密顿偏微分方程组整体能量守恒的数值格式、局部能量守恒的数值格式、局部动量守恒的数值格式．

本文通过引入正则动量，证明DGH方程具有多辛结构．首先给出多辛哈密顿格式，以及此格式具有的多辛守恒律、局部能量守恒律和局部动量守恒律．然后给出多辛哈密顿方程的离散保结构算法格式，即局部能量保结构算法格式和局部动量保结构算法格式，进而给出DGH方程的保结构算法．最后通过两个数值模拟算例，验证算法性能．

1 微分方程的多辛哈密顿形式及守恒律

Bridges首先发现，大量的偏微分方程可以写成下列多辛哈密顿偏微分方程的形式[15]：

(1)

定理1[15]根据Bridges多辛理论，偏微分方程(1)满足多辛守恒律

(2)

其中W、k分别表示t和x方向上的辛结构，具体表达式为

定理2[15]根据Bridges多辛理论，偏微分方程(1)满足局部能量守恒律：

(3)

局部动量守恒律：

(4)

其中

E为能量密度；F为能量流；I为动量密度；G为动量流．

如果z(t，x)关于x是周期函数或者满足齐次边界条件，偏微分方程(1)满足整体能量和整体动量守恒律：

(5)

2多辛哈密顿偏微分方程的保结构算法

为了研究问题方便，首先引入下面符号：

向前差分算子

(6)

平均算子

(7)

上面的算子满足DtDx=DxDt，AtAx=AxAt，DA=AD，及推广的Leibniz法则：

Dx(uv)j=uj+1Dxvj+Dxujvj

Dt(uv)j=uj+1Dtvj+Dtujvj

2.1局部能量保结构算法

利用上面的算子，对空间方向进行离散，得到哈密顿系统(1)的半离散格式：

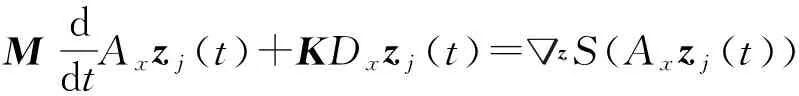
MddtAxzj(t)+KDxzj(t)=zS(Axzj(t))

(8)

用AVF方法对半离散格式(8)时间方向进行离散，得到哈密顿系统(1)的全离散格式：

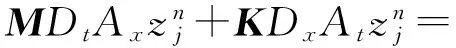
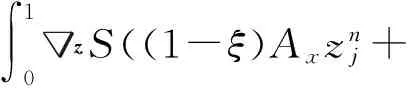
∫10zS((1-ξ)Axznj+

(9)

为了分析全离散格式(9)的局部能量守恒律和局部动量守恒律，引入定义：

定义1 记

(10)

(11)

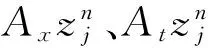
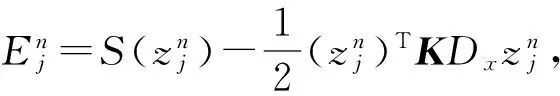
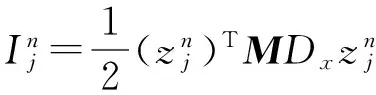
记

(12)

(13)

称εn、ηn分别是整体能量和整体动量．

定理3[19]全离散格式(9)满足离散局部能量守恒律：

定理4[19]如果满足周期边界条件z(x+L，t)=z(x，t)，全离散格式(9)满足离散整体能量守恒律：

εn+1=εn

2.2局部动量保结构算法

对时间方向进行离散，得到哈密顿系统(1)的半离散格式：

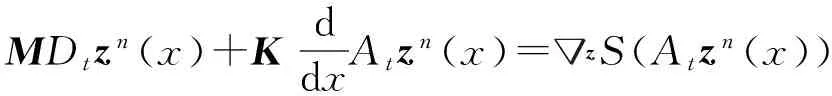
MDtzn(x)+KddxAtzn(x)=zS(Atzn(x))

(14)

用AVF方法对半离散格式(14)空间方向进行离散，得到哈密顿系统(1)的全离散格式：

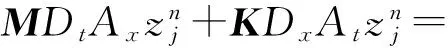
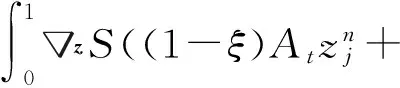
∫10zS((1-ξ)Atznj+

(15)

定理5[19]全离散格式(15)满足离散局部动量守恒律：

定理6[19]如果满足周期边界条件z(x+L，t)=z(x，t)，全离散格式(15)满足离散整体动量守恒律：

ηn+1=ηn

3一类DGH方程的新保结构算法

1895年，Korteweg和他的学生deVries研究无黏滞、不可压缩流体运动时得到一个浅水波方程(在长波和小振幅条件下)，即KdV方程：

ut+2ωux+3uux+γuxxx=0

(16)

该方程是非线性水波理论研究的一个基本方程．1993年，美国阿尔莫斯国家实验室的Camassa和Holm考虑重力作用下浅水层自由表面的水波运动时，推导出Camassa-Holm方程(简称C-H方程)：

ut+2ωux+3uux-α2uxxt-α2(uuxxx+2uxuxx)=0

(17)

该方程成为非线性水波理论研究的另一类重要的基本方程．2001年，Dullin、Gottwald和Holm从Euler方程出发，得到了一类带线性和非线性色散项的新型浅水波方程，即DGH方程[1]：

ut+2ωux+3uux+γuxxx-α2uxxt-

α2(uuxxx+2uxuxx)=0

(18)

当α=0时，DGH方程变为KdV方程，当γ=0时，DGH方程转化为C-H方程．

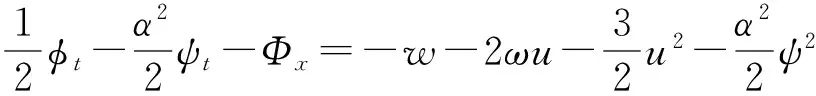
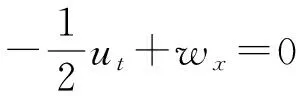
-φx=-u，

ux=ψ，

(19)

定义状态变量z=(uφwΦψ)，可以把系统(19)写成多辛哈密顿偏微分方程的形式(1)，其中

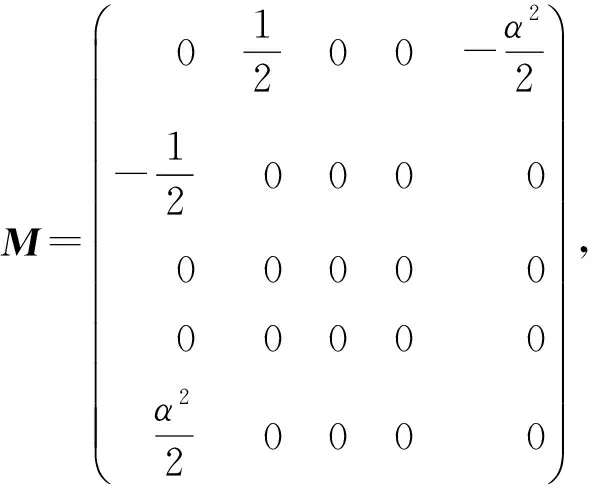
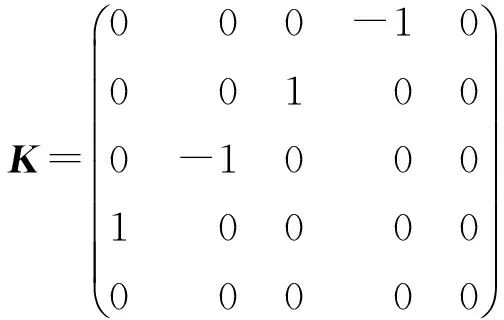
哈密顿函数为

系统(19)满足多辛守恒律(2)，其中

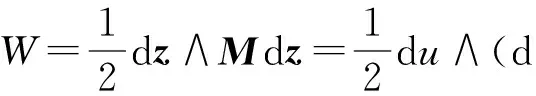
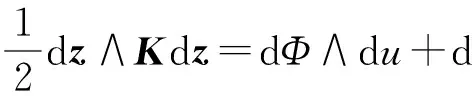
系统(19)满足局部能量守恒律(3)，其中

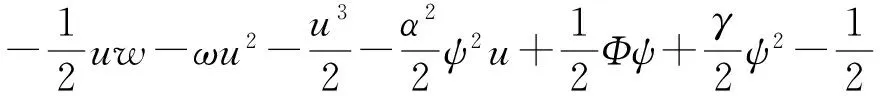
系统(19)满足局部动量守恒律(4)，其中

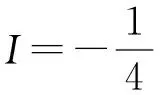
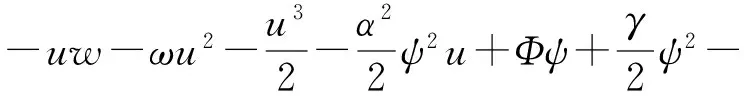
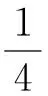
3.1DGH方程的局部能量保结构算法

对系统(18)的等价方程组(19)应用局部能量保结构算法(9)可得

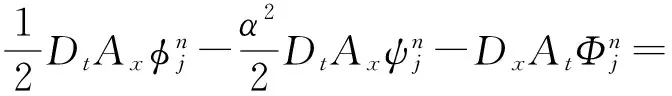
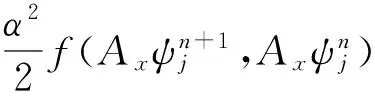
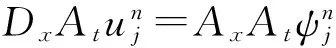
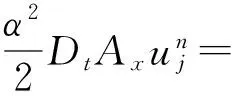
(20)

其中

全离散格式(20)满足离散局部能量守恒律：

(21)

消去辅助变量可以得到局部能量守恒格式为

(22)

3.2DGH方程的局部动量保结构算法

对系统(18)的等价方程组(19)应用局部动量保结构算法(15)可得

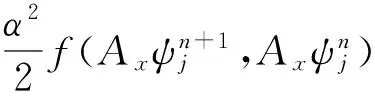
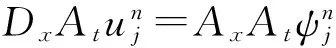
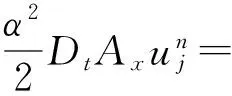
(23)

其中

全离散格式(23)满足离散局部动量守恒律：

(24)

消去辅助变量可以得到局部动量守恒格式为

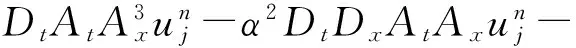
(25)

4数值算例

下面应用局部能量保结构算法和局部动量保结构算法对DGH方程(18)进行数值模拟，并且分析该数值方法的离散局部能量和动量守恒律误差．本文将对局部能量保结构算法、局部动量保结构算法与有限差分法(中心差分法)的数值结果和精确解进行比较．对局部能量保结构算法、局部动量保结构算法与有限差分法取相同的空间和时间步长．

4.1DGH方程的局部能量保结构算法数值模拟

4.1.1孤立波A取参数α=1，ω=1，γ=1，考虑DGH方程(18)的孤立波的初值条件为

由文献[30]，可以得到DGH方程(18)的初值问题有孤立波解

取空间步长Δx=0.01，时间步长Δt=0.05，计算到T=60．计算结果见表1和图1、2．表1给出了有限差分法、局部能量保结构算法和精确解的比较．图1给出了DGH方程孤立波的初值问题随时间的演化图．图2给出了DGH方程孤立波初值问题的局部能量保结构算法的局部动量守恒律误差．

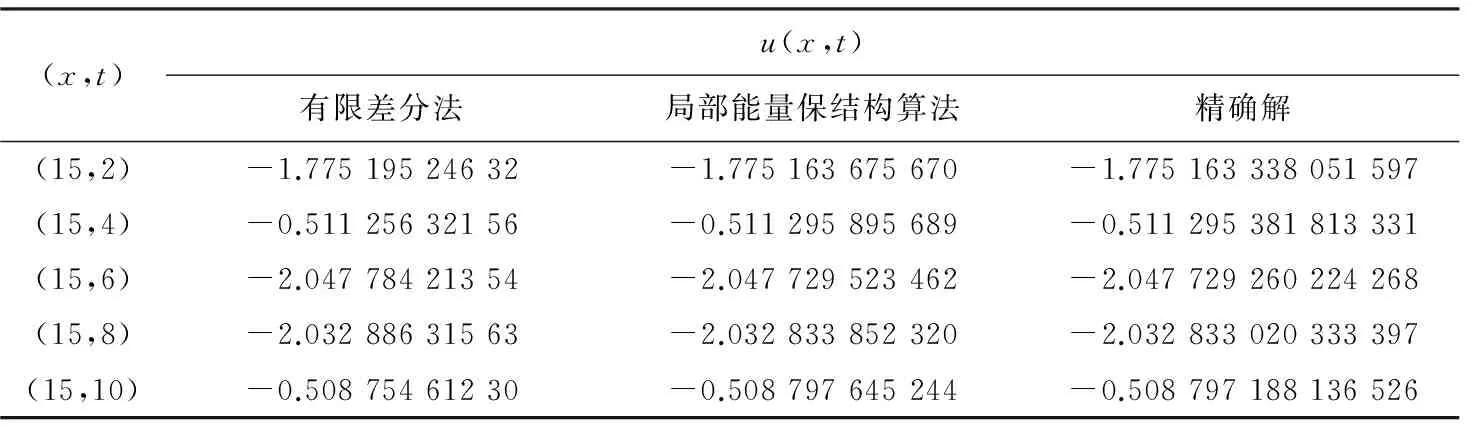
表1　有限差分法、局部能量保结构算法和精确解的比较(孤立波A)

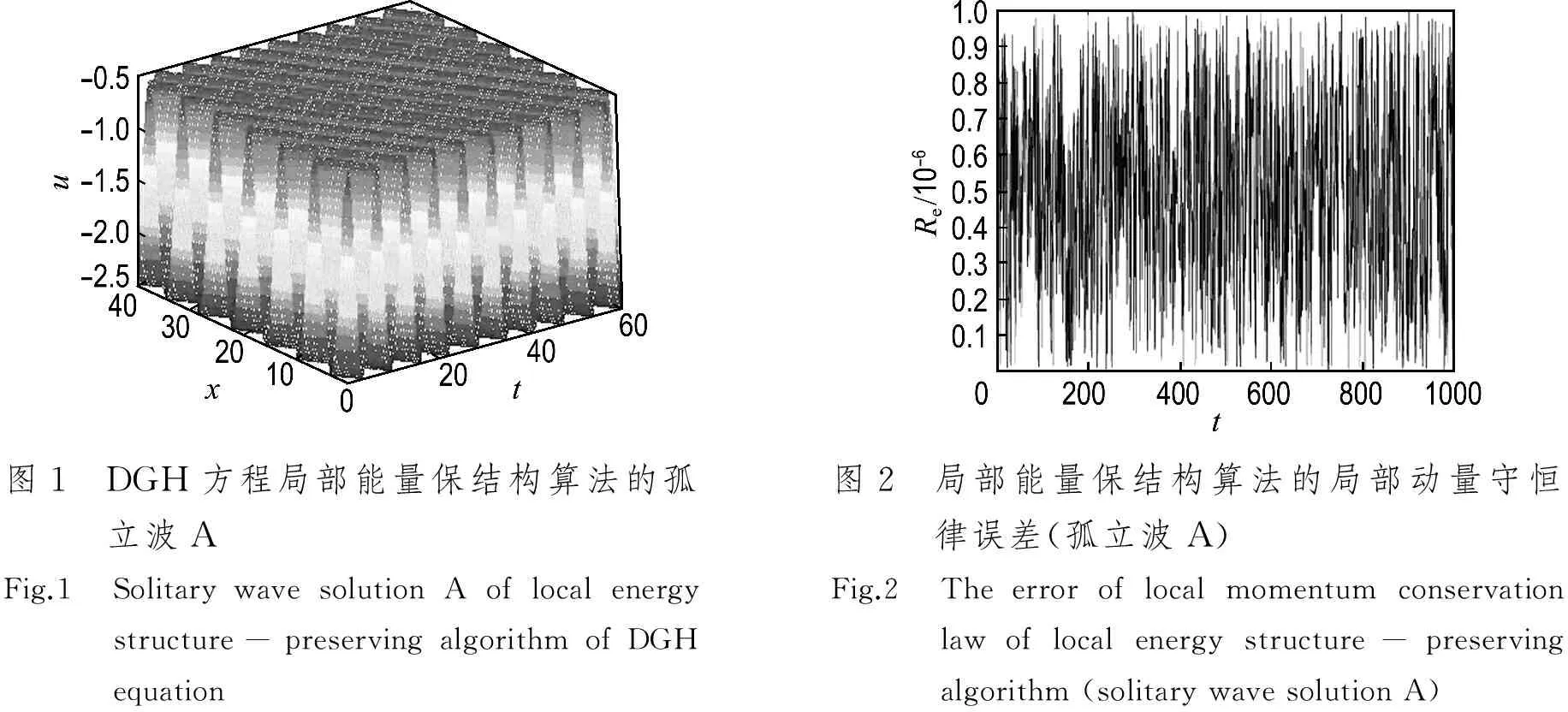
图1 DGH方程局部能量保结构算法的孤立波AFig.1 SolitarywavesolutionAoflocalenergystructure-preservingalgorithmofDGHequation图2 局部能量保结构算法的局部动量守恒律误差(孤立波A)Fig.2 Theerroroflocalmomentumconservationlawoflocalenergystructure-preservingalgorithm(solitarywavesolutionA)

4.1.2孤立波B取参数α=1，ω=1，γ=1，考虑DGH方程(18)的孤立波的初值条件为

由文献[30]，可以得到DGH方程(18)的初值问题有孤立波解

取空间步长Δx=0.01，时间步长Δt=0.05，计算到T=60．计算结果见表2和图3、4．表2给出了有限差分法、局部能量保结构算法和精确解的比较．图3给出了DGH方程孤立波的初值问题随时间的演化图．图4给出了DGH方程孤立波初值问题的局部能量保结构算法的局部动量守恒律误差．

4.2DGH方程的局部动量保结构算法数值模拟

4.2.1孤立波A取参数α=1，ω=1，γ=1，考虑DGH方程(18)的孤立波的初值条件为

由文献[30]，可以得到DGH方程(18)的初值问题有孤立波解

取空间步长Δx=0.01，时间步长Δt=0.05，计算到T=60．计算结果见表3和图5、6．表3给出了有限差分法、局部动量保结构算法和精确解的比较．图5给出了DGH方程孤立波的初值问题随时间的演化图．图6给出了DGH方程孤立波初值问题的局部动量保结构算法的局部能量守恒律误差．

4.2.2孤立波B取参数α=1，ω=1，γ=1，考虑DGH方程(18)的孤立波的初值条件为

由文献[30]，可以得到DGH方程(18)的初值问题有孤立波解

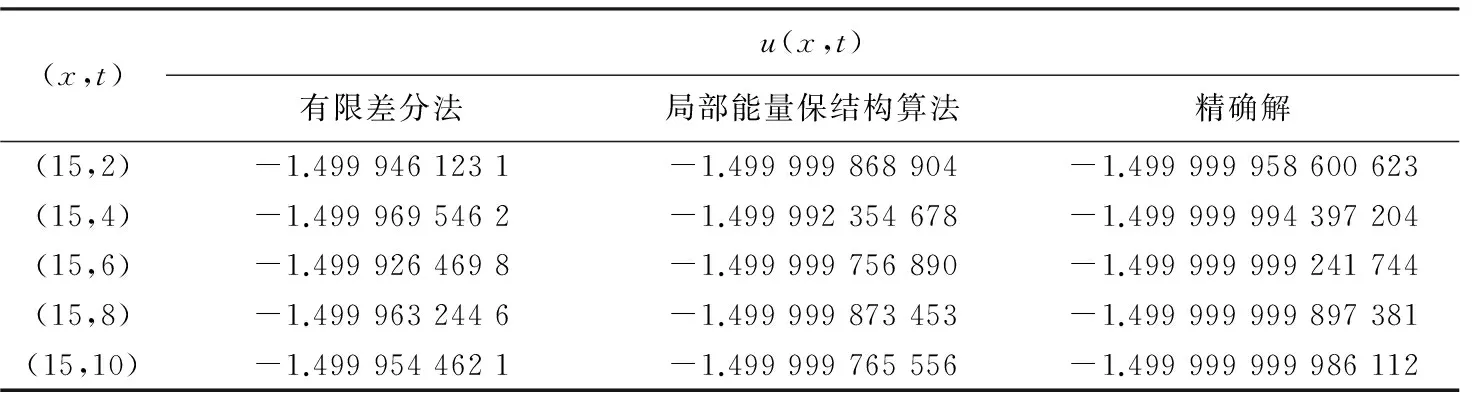
表2　有限差分法、局部能量保结构算法和精确解的比较(孤立波B)

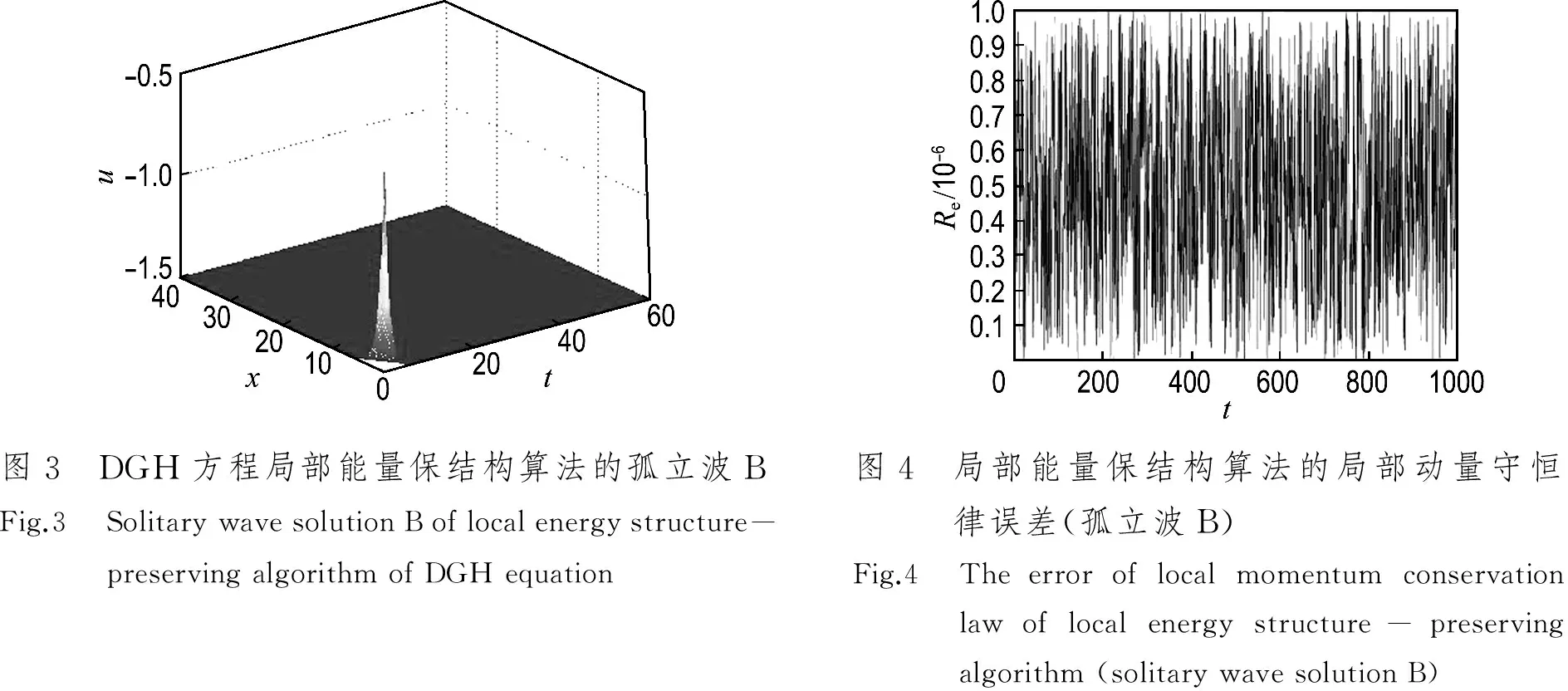
图3 DGH方程局部能量保结构算法的孤立波BFig.3 SolitarywavesolutionBoflocalenergystructure-preservingalgorithmofDGHequation图4 局部能量保结构算法的局部动量守恒律误差(孤立波B)Fig.4 Theerroroflocalmomentumconservationlawoflocalenergystructure-preservingalgorithm(solitarywavesolutionB)

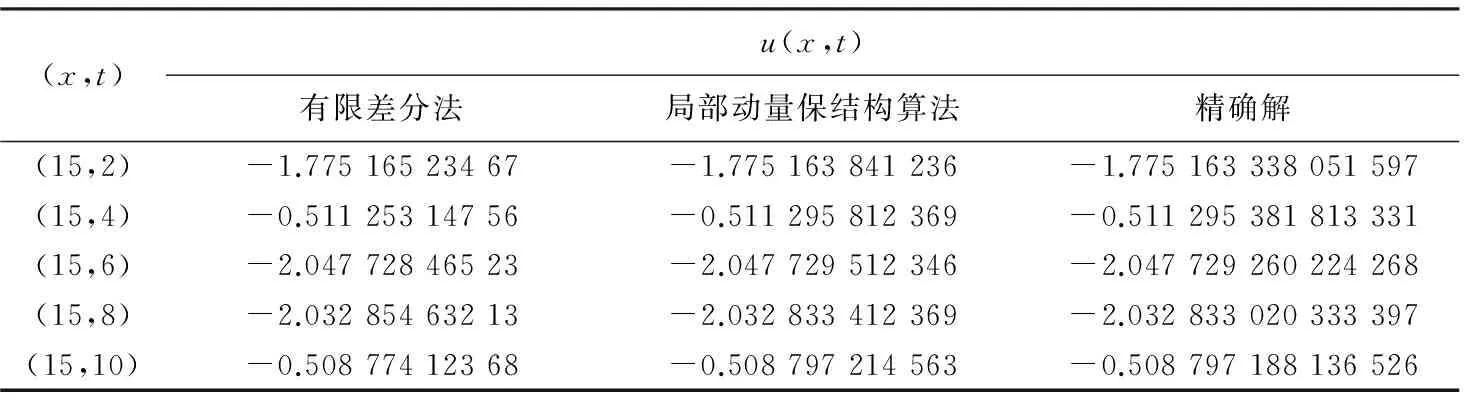
表3　有限差分法、局部动量保结构算法和精确解的比较(孤立波A)

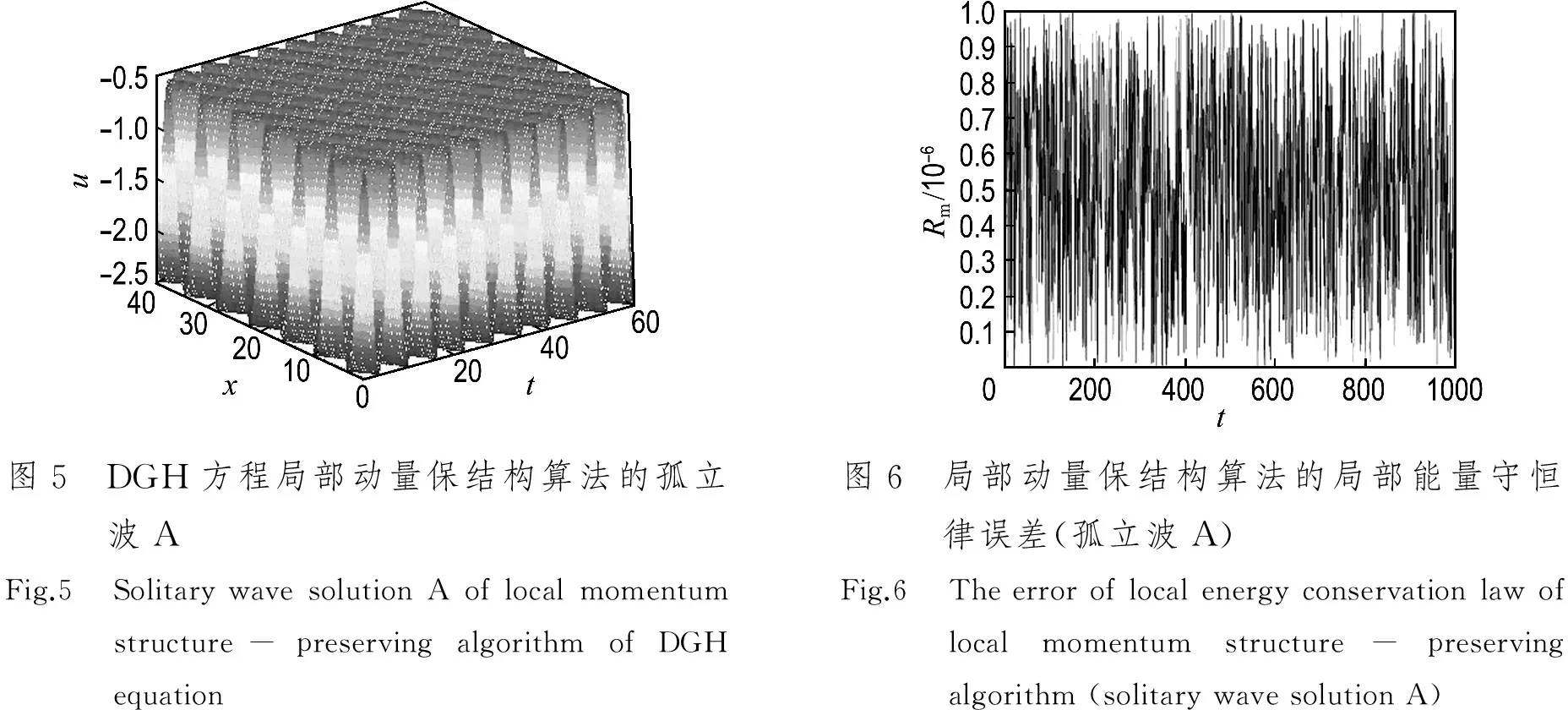
图5 DGH方程局部动量保结构算法的孤立波AFig.5 SolitarywavesolutionAoflocalmomentumstructure-preservingalgorithmofDGHequation图6 局部动量保结构算法的局部能量守恒律误差(孤立波A)Fig.6 Theerroroflocalenergyconservationlawoflocalmomentumstructure-preservingalgorithm(solitarywavesolutionA)

取空间步长Δx=0.01，时间步长Δt=0.05，计算到T=60．计算结果见表4和图7、8．表4给出了有限差分法、局部动量保结构算法和精确解的比较．图7给出了DGH方程孤立波的初值问题随时间的演化图．图8给出了DGH方程孤立波初值问题的局部动量保结构算法的局部能量守恒律误差．

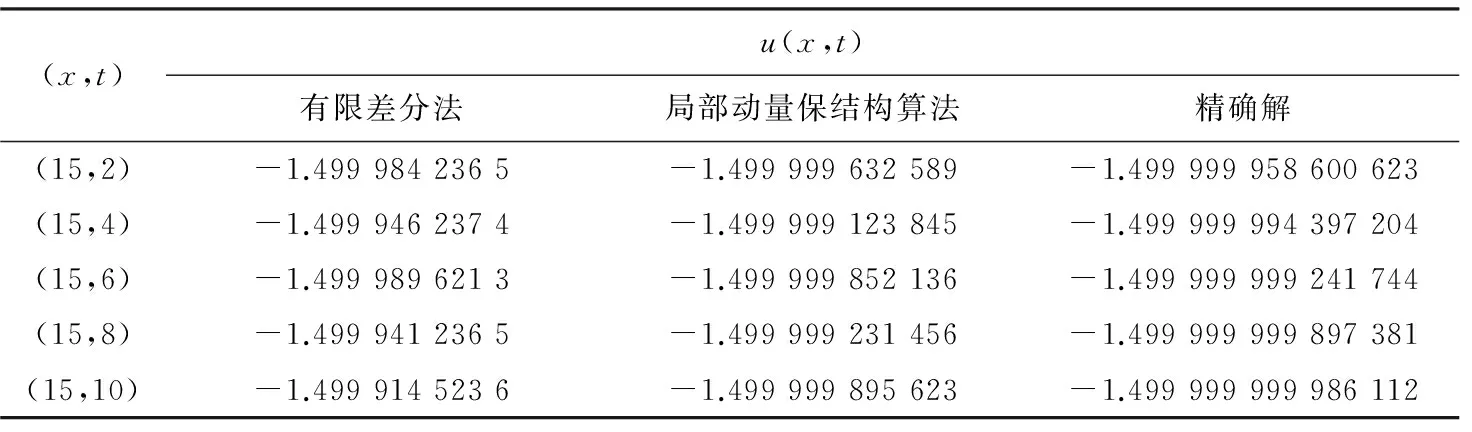
表4　有限差分法、局部动量保结构算法和精确解的比较(孤立波B)

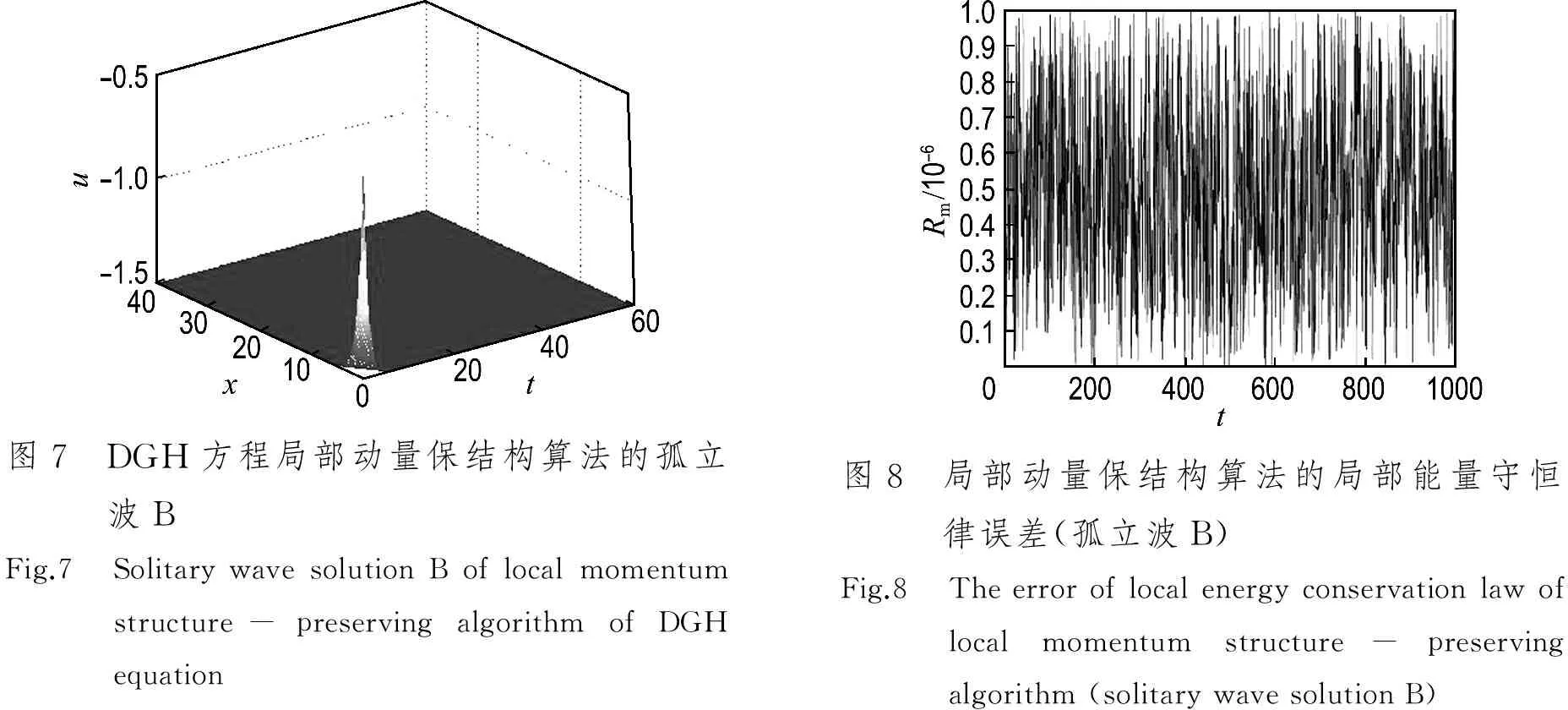
图7 DGH方程局部动量保结构算法的孤立波BFig.7 SolitarywavesolutionBoflocalmomentumstructure-preservingalgorithmofDGHequation图8 局部动量保结构算法的局部能量守恒律误差(孤立波B)Fig.8 Theerroroflocalenergyconservationlawoflocalmomentumstructure-preservingalgorithm(solitarywavesolutionB)

5结语

本文利用能量保结构算法和动量保结构算法对一类DGH方程的初值问题进行了数值模拟．给出了DGH方程的初值问题的离散格式．从数值模拟得到的图1～8、表1～4说明，能量保结构算法和动量保结构算法能够很好地保持孤子解的基本几何性质，并具有良好的长时间数值行为．

参考文献：

[1] Dullin H R, Gottwald G A, Holm D D. An integrable shallow water equation with linear and nonlinear dispersion [J]. Physical Review Letters, 2001, 87(19):194501.

[2]Camassa R, Holm D D. An integrable shallow water equation with peaked solitons [J]. Physical Review Letters, 1993, 71(11):1661-1664.

[3]TIAN Li-xin, YIN Jiu-li. New compacton solutions and solitary wave solutions of fully nonlinear generalized Camassa-Holm equations [J]. Chaos, Solitons & Fractals, 2004, 20(2):289-299.

[4]Fisher M, Schiff J. The Camassa-Holm equation:conserved quantities and the initial value problem [J]. Physics Letters A, 1999, 259(5):371-376.

[5]Clarkson P A, Mansfield E L, Priestley T J. Symmetries of a class of nonlinear third-order partial differential equations [J]. Mathematical and Computer Modelling, 1997, 25(8-9):195-212.

[6]Kraenkel R A, Senthilvelan M, Zenchuk A I. On the integrable perturbations of the Camassa-Holm equation [J]. Journal of Mathematical Physics, 2000, 41(5):3160-3169.

[7]DING Dan-ping, TIAN Li-xin. The attractor on dissipative Camassa-Holm equation [J]. Acta Mathematicae Applicatae Sinica, 2004, 27(3):536-545.

[8]TIAN Li-xin, XU Gang, LIU Zeng-rong. The concave or convex peaked and smooth soliton solutions of Camassa-Holm equation [J]. Applied Mathematics and Mechanics, 2002, 23(5):557-567.

[9]TIAN Li-xin, SONG Xiu-ying. New peaked solitary wave solutions of the generalized Camassa-Holm equation [J]. Chaos, Solitons & Fractals, 2004, 19(3):621-637.

[10]TIAN Li-xin, GUI Gui-long, LIU Yue. On the well-posedness problem and the scattering problem for the Dullin-Gottwald-Holm equation [J]. Communications in Mathematical Physics, 2005, 257(3):667-701.

[11]GUO Bo-ling, LIU Zheng-rong. Peaked wave solutions of CH-γ equation [J]. Science in China Series A:Mathematics, 2003, 46(5):696-709.

[12]YIN Zhao-yang. Well-posedness, blowup, and global existence for an integrable shallow water equation [J]. Discrete and Continuous Dynamical Systems, 2004, 11(2-3):393-411.

[13]JU Lin. On solution of the Dullin-Gottwald-Holm equation [J]. International Journal of Nonlinear Science, 2006, 1(1):43-48.

[14]Marsden J E, Patrick G W, Shkoller S. Multisymplectic geometry, variational integrators, and nonlinear PDEs [J]. Communications in Mathematical Physics, 1998, 199(2):351-395.

[15]Reich S. Multi-symplectic Runge-Kutta collocation methods for Hamiltonian wave equations [J]. Journal of Computational Physics, 2000, 157(2):473-499.

[16]LV Zhong-quan, WANG Yu-shun, SONG Yong-zhong. A new multi-symplectic integration method for the nonlinear Schrödinger equation [J]. Chinese Physics Letters, 2013, 30(3):030201.

[17]GONG Yue-zheng, CAI Jia-xiang, WANG Yu-shun. Multi-symplectic Fourier pseudospectral method for the Kawahara equation [J]. Communications in Computational Physics, 2013, 16(1):35-55.

[18]WANG Yu-shun, HONG Jia-lin. Multi-symplectic algorithms for Hamiltonian partial differential equations [J]. Communication on Applied Mathematics and Computation, 2013, 27(2):163-230.

[19]GONG Yue-zheng, CAI Jia-xiang, WANG Yu-shun. Some new structure-preserving algorithms for general multi-symplectic formulations of Hamiltonian PDEs [J]. Journal of Computational Physics, 2014, 279:80-102.

[20]LIU Ting-ting, QIN Meng-zhao. Multisymplectic geometry and multisymplectic Preissman scheme for the KP equation [J]. Journal of Mathematical Physics, 2002, 43(8):4060-4077.

[21]TIAN Yi-min, QIN Meng-zhao, ZHANG Yong-ming,etal. The multisymplectic numerical method for Gross-Pitaevskii equation [J]. Computer Physics Communications, 2008, 178(6):449-458.

[22]WANG Yu-shun, WANG Bin, QIN Meng-zhao. Concatenating construction of the multisymplectic schemes for 2+1-dimensional sine-Gordon equation [J]. Science in China Series A:Mathematics, 2004, 47(1):18-30.

[23]Escher J, Lechtenfeld O, YIN Zhao-yang. Well-posedness and blow-up phenomena for the 2-component Camassa-Holm equation [J]. Discrete and Continuous Dynamical Systems, 2007, 19(3):493-513.

[24]KONG Ling-hua, LIU Ru-xun, ZHENG Xiao-hong. A survey on symplectic and multi-symplectic algorithms [J]. Applied Mathematics and Computation, 2007, 186(1):670-684.

[25]Leimkuhler B, Reich S. Simulating Hamiltonian Dynamics [M]. Cambridge:Cambridge University Press, 2005.

[26]Islas A L, Schober C M. Backward error analysis for multisymplectic discretizations of Hamiltonian PDEs [J]. Mathematics and Computers in Simulation, 2005, 69(3-4):290-303.

[27]Moore B, Reich S. Backward error analysis for multi-symplectic integration methods [J]. Numerische Mathematik, 2003, 95(4):625-652.

[28]Celledoni E, McLachlan R I, Owren B,etal. On conjugate B-series and their geometric structure [J]. Journal of Numerical Analysis, Industrial and Applied Mathematics, 2010, 5(1-2):85-94.

[29]CHEN Yao, SUN Ya-juan, TANG Yi-fa. Energy-preserving numerical methods for Landau-Lifshitz equation [J]. Journal of Physics A: Mathematical and Theoretical, 2011, 44(59):295207.

[30]殷久利,田立新. 一类非线性色散方程中的新型奇异孤立波 [J]. 物理学报, 2009, 58(6):3632-3636.

YIN Jiu-li, TIAN Li-xin. New exotic solitary waves in one type of nonlinear dispersive equations [J]. Acta Physica Sinica, 2009, 58(6):3632-3636. (in Chinese)

文章编号：1000-8608(2016)04-0432-09

收稿日期：2015-11-20；修回日期: 2016-04-12．

基金项目:云南省教育厅科学研究基金资助项目(2015y490)；普洱学院创新团队项目(CXTD003).

作者简介:王俊杰*(1981-)，男，硕士，副教授，E-mail:pedxsxxwjj@163.com.

中图分类号：O29

文献标识码：A

doi:10.7511/dllgxb201604016

Research on new structure-preserving algorithms for a DGH equation

WANGJun-jie*1,2

( 1.Department of Mathematics, Pu′er University, Pu′er 665000, China；2.School of Mathematics, Northwest University, Xi′an 710127, China )

Abstract：DGH equation is an important nonlinear wave equation and has broad application prospect. Numerical method for the equation is studied based on the multi-symplectic theory in Hamilton system. The average vector field (AVF) method is used to discretize the Hamilton system, and local energy structure-preserving algorithm and local momentum structure-preserving algorithm are constructed to solve the DGH equation. The numerical examples show that the two kinds of structure-preserving algorithms have good long-time numerical stability.

Key words：Hamilton system; structure-preserving algorithms; multi-symplectic theory; DGH equation