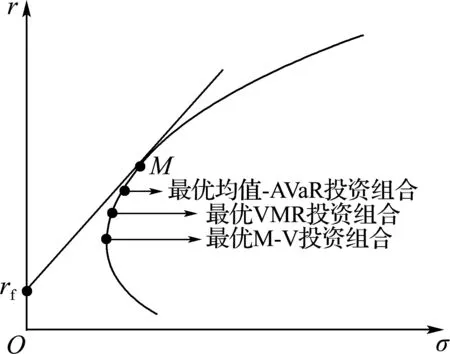
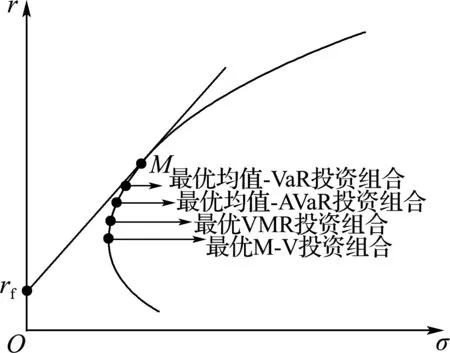
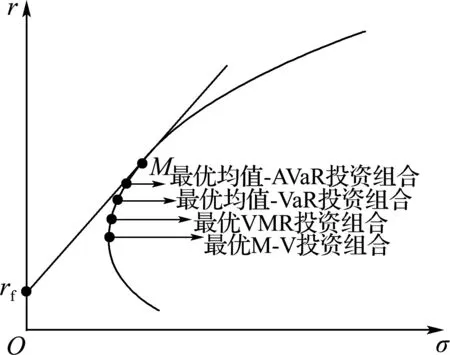
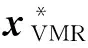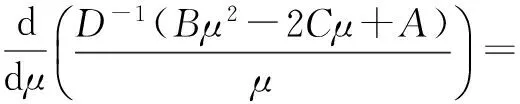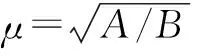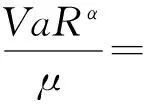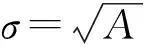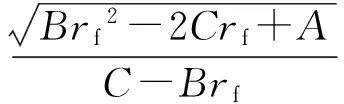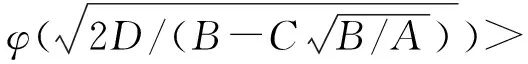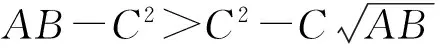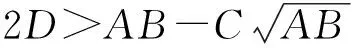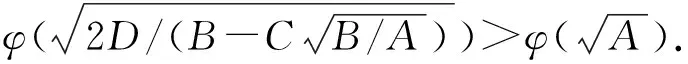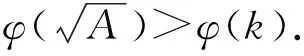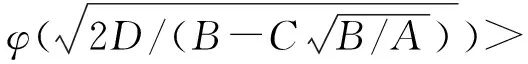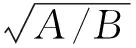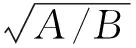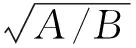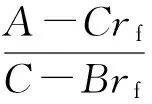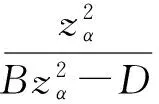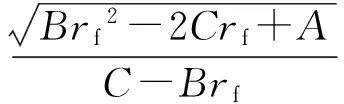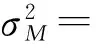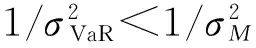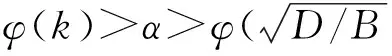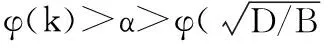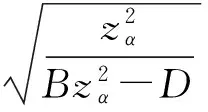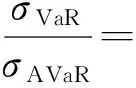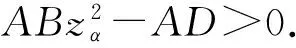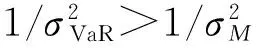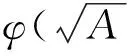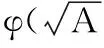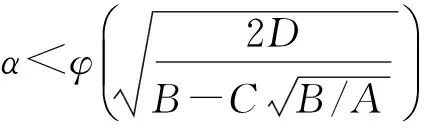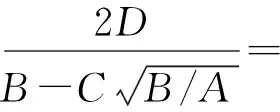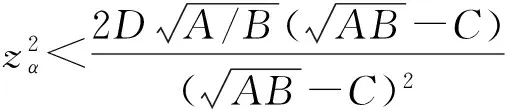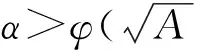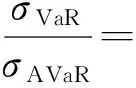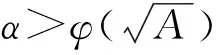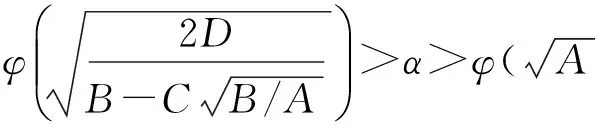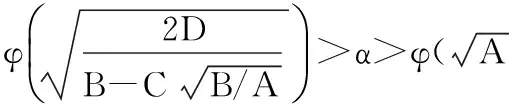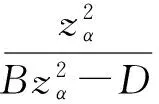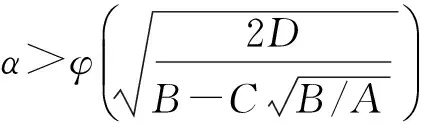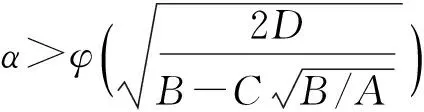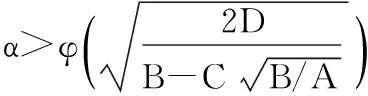几种最优投资组合在有效边界上相对位置

周 伊 佳，　于 　 波

( 大连理工大学 数学科学学院, 辽宁 大连　116024 )



几种最优投资组合在有效边界上相对位置

周 伊 佳，于 波*

( 大连理工大学 数学科学学院, 辽宁 大连116024 )

摘要：讨论了均值-VaR、均值-AVaR、方差-均值比等风险-收益投资组合优化模型的最优解的有效性．基于Markowitz均值-方差模型和有效边界理论，证明了如果各模型的最优投资组合存在，则一定位于均值-方差有效边界上．计算了各投资组合模型最优解处的均值和标准差，根据计算结果讨论了各模型的最优投资组合在有效边界上的位置．特别地，均值-VaR模型的最优投资组合在有效边界上的位置与置信水平有关．

关键词：投资组合优化模型；最优投资组合；有效边界

0引言

20世纪50年代，Markowitz首创了经典的投资组合理论：均值-方差(mean-variance，M-V)投资组合优化模型[1]，它奠定了现代投资组合的理论基础．在M-V模型中方差被视为风险估计．20世纪80年代以来，随着金融市场的飞速发展及信息技术的创新，在Markowitz投资理论框架下产生了均值-VaR(Value-at-Risk)投资组合模型．VaR，是指在市场正常波动下以及在一定的概率水平下，于给定的置信区间内，金融资产或资产组合在未来一段时间内可能受到的最大损失[2]．人们对VaR约束下的投资组合策略的选择问题进行了研究[3-5]．根据VaR风险度量，张红兵等[6]提出多阶段资产组合选择均值-VaR模型．王尚户等[2]利用均值-VaR方法，提出了均值-AVaR(average Value-at-Risk)模型，并在一定的置信水平下得到了投资组合的均衡理论．

投资者想要获得更高的收益，就要承受更大的风险；反之要降低风险，则获得的收益也随之减少．由于风险与收益存在着这样的联系，那么只分别考虑最小风险和最大收益的投资组合决策方法往往不能较好地全面权衡收益与风险之间的关系．因此本文基于均值-方差模型的有效边界理论，研究一系列关于收益-风险的优化模型的最优投资组合，这些优化模型在某种程度上能够均衡均值与方差，即收益与风险，在一定程度上为投资者对资源做出最优的投资组合规划提供参考．

1投资组合模型

首先介绍一些收益-风险投资组合优化模型及它们的最优解处的收益和标准差．

1.1均值-方差模型

Markowitz的均值-方差(M-V)模型是经典的投资组合优化模型．设在投资组合问题中，投资者选择n种风险证券，证券的收益率向量r=(r1

r2…rn)T，其中ri表示第i种证券的期望收益率；投资比例向量x=(x1x2…xn)T，xi是投资第i种证券的比例；投资组合的协方差矩阵V=(vij)n×n，其中vij表示第i种证券和第j种证券的协方差．投资组合的期望收益与方差分别为μ=rTx，σ2=xTVx．则M-V投资组合模型[2]为

(1)

假定协方差矩阵V=(vij)n×n是正定的，根据Lagrange乘子法求得式(1)的最优解为[2]

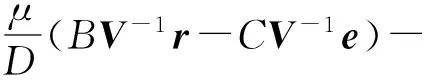
(2)

式中：A=rTV-1r，B=eTV-1e，C=eTV-1r，D=AB-C2，根据定义可知，A、B、C、D均大于零．将式(2)代入σ2=xTVx，整理得到M-V投资组合的有效边界[2]

(3)

即

σ2=D-1(Bμ2-2Cμ+A)

(4)

1.2最小化风险-收益比投资组合模型

定义方差-均值比(variance-mean ratio，VMR)模型为

(5)

其经济学含义是投资者在投资一定数额的资产后，平均每一单位收益所承受的风险波动．模型意在使得单位收益率下所承受的风险波动越小越好．

1.3均值-VaR与均值-AVaR投资组合模型

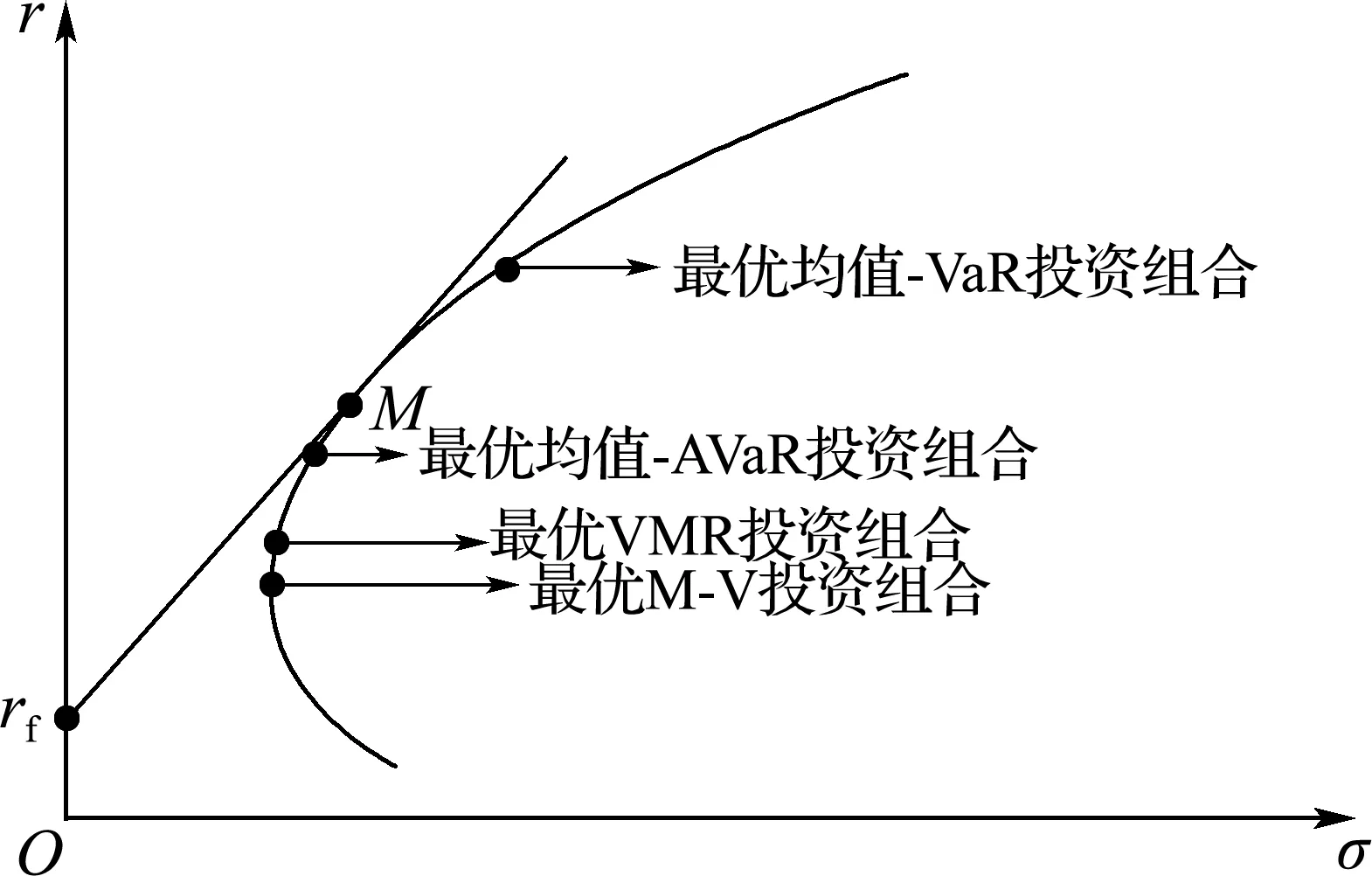
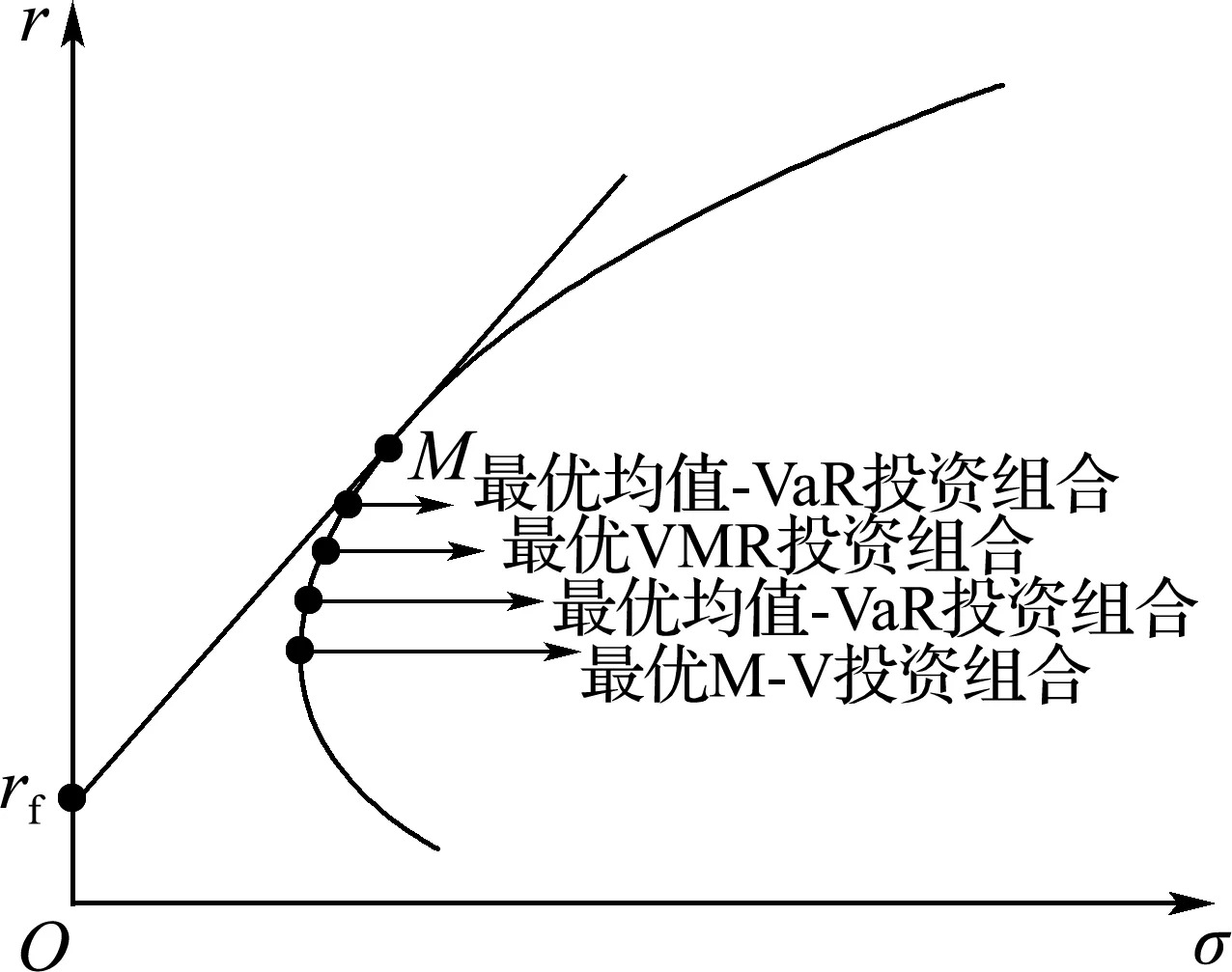
VaR在概率统计中的表达式[7]为

Prob(r

(6)

其中r表示投资组合X的收益率，α(0．5<α<1.0)为置信水平，且VaRα[r]>0．假设不存在卖空行为，资产收益率与投资组合收益率r均服从正态分布，即r～N(μ，σ2)，于是式(6)可变形为

VaRα[r]=zασ-μ

(7)

其中zα表示标准正态分布的α分位点，则有zα=φ-1(α)，φ(·)表示标准正态分布的分布函数[8]．

用VaR代替式(1)中的方差作为目标函数，得到均值-VaR模型[2]：

(8)

另外，模型(8)的边界有如下形式：

根据模型(8)，文献[2]中给出的均值-AVaR投资组合模型为

(9)

显然，此模型表示投资者在投资一定数额的资产后，在给定的置信水平下，平均每一单位收益所承受的损失额，使得在单位收益率下所承受的损失额越小越好[2]．

2投资组合模型解的有效性分析

定理1 若全局最小VMR投资组合存在，那么它一定是均值-方差有效的．

□

根据M-V的有效边界理论，VMR模型的解是有效解，则可以将式(4)代入模型(5)的目标得到

在上式中对μ求导，令

类似地，可以得到下面的结论：

定理2 若全局最小均值-AVaR投资组合存在，那么它一定是均值-方差有效的．

证明 略．

根据最小均值-AVaR模型的有效性，可以将式(4)代入模型(9)得到

1972年Merton[10]指出：在某一投资组合中若存在无风险证券，设无风险收益率为rf，当且仅当此资本市场线为

定理3 设与有效边界相切的资本市场线斜率为k，则有

且任取置信水平α满足α>φ(k)，全局最小均值-VaR投资组合存在，且是均值-方差有效的．

由于无风险收益率一定满足rf<μ=C/B，否则问题将没有意义，从而有

再根据C-Brf>0，有B2rf2-2CBrf+C2>0，且已知D=AB-C2，B、D均大于零，因此有

B2rf2-2CBrf+AB>D

综上所述，对与有效边界相切的资本市场线斜率k，有

□

3投资组合在有效边界上的相对位置

前文中给出了各投资组合模型最优解的有效性，接下来研究各模型的最优解在有效边界上的相对位置．

定理4 在有效边界上，从下到上对应的投资组合为最优M-V投资组合、最优VMR投资组合与最优均值-AVaR投资组合和切点M．

其次，均值-AVaR投资组合的期望收益率为A/C，与VMR投资组合的期望收益率作比较得到

已知D=AB-C2>0，因此μM/μAVaR>1，可见最优均值-AVaR投资组合位于M点之下．

□

根据定理4，这4种最优投资组合在有效边界上的相对位置如图1所示．

图1　最优投资组合在有效边界上的相对位置

定理5 设与有效边界相切的资本市场线斜率为k，任取置信水平α满足

则最优均值-VaR投资组合在切点M之上．

由于α<φ(k)，有D/zα2>D/k2，故

□

综上，根据定理4和定理5的结论可知：在某一投资组合中存在无风险证券时，取资本市场线的斜率为k，任取置信水平α满足

则各最优投资组合在有效边界上从下到上的排列依次为最优M-V投资组合、VMR投资组合、均值-AVaR投资组合、切点M和均值-VaR投资组合．如图2所示．

定理6 设与有效边界相切的资本市场线斜率为k，任取置信水平α满足

则最优均值-VaR投资组合在有效边界上位于最优均值-AVaR投资组合之上、M点之下．

由于α>φ(k)，即zα>k，有D/zα2B-D/k2．并且已知

□

综上所述，根据定理4和定理6的结论可知：在某一投资组合中存在无风险证券时，取资本市场线的斜率为k，任取置信水平α满足

则最优M-V投资组合、VMR投资组合、均值-AVaR投资组合、均值-VaR投资组合和切点M在有效边界上的排列如图3所示．

定理7 任取置信水平α满足

则最优均值-VaR投资组合位于最优VMR投资组合之上、最优均值-AVaR投资组合之下．

证明 由定理3知道对任意的置信水平α满足已知条件，全局最小均值-VaR投资组合存在，且在此置信水平下，

由于

整理得到

(10)

从而说明了最优VaR投资组合位于最优VMR投资组合之上．

□

根据定理4和定理7得到这样的结论：在某一投资组合中存在无风险证券时，取资本市场线的斜率为k，任取置信水平α满足

则在有效边界上从下到上的排列依次为最优M-V投资组合、VMR投资组合、均值-VaR投资组合、均值-AVaR投资组合和切点M．如图4所示．

定理8 任取置信水平α满足

则最优均值-VaR投资组合位于最优VMR投资组合之下、最优M-V投资组合之上．

类似于定理7的证明，将不等式变形后可以得到

从而说明了最优VMR投资组合位于最优均值-VaR投资组合之上．

□

根据定理4和定理8的结论可知：在某一投资组合中存在无风险证券时，取资本市场线的斜率为k，任取置信水平α满足

则最优M-V投资组合、均值-VaR投资组合、VMR投资组合、均值-AVaR投资组合和切点M在有效边界上的排列如图5所示．

4结语

本文基于均值-方差模型的有效边界理论，证明了已有的一些投资组合优化模型的最优投资组合是均值-方差有效的．通过计算各模型最优解处的均值和标准差，分析了这些最优投资组合在有效边界上的相对位置，并给出了具体图形．利用给出的图形，投资者可以对这些最优投资策略的相对保守程度有更直观的认识，从而，根据自己的投资喜好，选择适合自己的投资策略．

另外，本文也指出，全局最小M-V投资组合、VMR投资组合、均值-AVaR投资组合与切点M在有效边界上的相对位置是不变的．但在不同的置信水平下，最优均值-VaR模型的投资组合在有效边界上的相对位置会发生改变．因此在利用均值-VaR模型确定投资决策时，要将α的影响因素考虑在内．

参考文献：

[1] Markowitz H. Portfolio selection [J]. The Journal of Finance, 1952, 7(1):77-91.

[2]王尚户,张崇岐. 基于均值-AVaR的投资组合均衡分析[J]. 广州大学学报(自然科学版), 2007, 6(6):11-13.

WANG Shang-hu, ZHANG Chong-qi. Mean-AVaR based portfolio balanced analysis [J]. Journal of Guangzhou University (Natural Science Edition), 2007, 6(6):11-13. (in Chinese)

[3]Alexandre G, Baptista A M. Economic implications of using mean-VAR model for portfolio selection:a comparison mean-variance with analysis [J]. Journal of Economic Dynamics & Control, 2002, 26(7-8):1159-1193.

[4]Basak S, Shapiro A. Value-at-risk-based risk management:optimal policies and asset prices [J]. Review of Financial Studies, 2001, 14(2):371-405.

[5]Gencay R, Selcuk F, Ulugulyagci A. High volatility, thick tails and extreme value theory in value-at-risk estimation [J]. Insurance:Mathematics and Economics, 2003, 33:337-356.

[6]张红兵,李高明,邸 涛. 多阶段资产组合选择均值-VaR模型的研究[J]. 纺织高校基础科学学报, 2005, 18(2):158-161.

ZHANG Hong-bing, LI Gao-ming, DI Tao. Study on mean-VaR models for multi-period portfolio selection [J]. Basic Sciences Journal of Textile Universities, 2005, 18(2):158-161. (in Chinese)

[7]屠新曙,王春峰. 最佳均值-VaR投资组合问题的研究[J]. 湘潭大学自然科学学报, 2002, 24(2):13-17.

TU Xin-shu, WANG Chun-feng. The mean-VaR optimum portfolio model [J]. Natural Science Journal of Xiangtan University, 2002, 24(2):13-17. (in Chinese)

[8]林旭东,巩前锦. 正态条件下均值-CVaR有效前沿的研究[J]. 管理科学, 2004, 17(3):52-55.

LIN Xu-dong, GONG Qian-jin. Research on the efficient frontier of mean-CVaR under normal distribution condition [J]. Management Sciences in China, 2004, 17(3):52-55. (in Chinese)

[9]荣喜民,武丹丹,张奎廷. 基于均值-VaR的投资组合最优化[J]. 数理统计与管理, 2005, 25(5):96-103.

RONG Xi-min, WU Dan-dan, ZHANG Kui-ting. Mean-VaR based portfolio optimization [J]. Journal of Applied Statistics and Management, 2005, 25(5):96-103. (in Chinese)

[10]Merton R C. An analytic derivation of the efficient portfolio frontier [J]. The Journal of Financial and Quantitative Analysis, 1972, 7(4):1851-1872.

文章编号：1000-8608(2016)04-0420-07

收稿日期：2015-12-05；修回日期: 2016-03-10．

基金项目:国家自然科学基金资助项目(11171051，重大计划91230103)；中央高校基本科研业务费专项资金资助项目(DUT15RC(3)037).

作者简介:周伊佳(1986-)，女，博士生，E-mail:zhouyijiadlut@gmail.com；于 波*(1963-)，男，教授，博士生导师，E-mail:yubo@dlut.edu.cn.

中图分类号：O224

文献标识码：A

doi:10.7511/dllgxb201604014

Relative location of optimal portfolios on efficient frontier

ZHOUYi-jia,YUBo*

( School of Mathematical Sciences, Dalian University of Technology, Dalian 116024, China )

Abstract：The validities of the optimal solutions of reward-risk portfolio optimization models are discussed, such as mean-VaR model, mean-AVaR model, mean-variance ratio model, etc.. It is proved that based on Markowitz mean-variance model and efficient frontier theory, if the optimal portfolios exist, they must be located on the efficient frontier of mean-variance. The mean and standard deviation of these models′ optimal solutions are calculated. According to the calculated results, the relative location of the optimal portfolios on the efficient frontier is discussed. Particularly, the location of mean-VaR model′s optimal portfolio on the efficient frontier varies with confidence levels.

Key words：portfolio optimization model; optimal portfolio; efficient frontier