含有势垒的一维无限深方势阱的矩阵解法

朱昌勇

（韶关学院 物理与机电工程学院， 广东 韶关 512005）



含有势垒的一维无限深方势阱的矩阵解法

朱昌勇

（韶关学院 物理与机电工程学院， 广东 韶关 512005）

摘要：无限深方势阱是量子力学中一个非常重要的模型，采用矩阵力学的方法解出了含有势垒的一维无限深方势阱的归一化波函数和能级，并且讨论了势垒趋于�势垒时能级的情况.

关键词：无限深势阱；波函数；势垒

一维对称无限深方势阱是量子力学中最基本的问题之一，大部分的量子力学都有讲述，而且可以通过奇偶性求得其解析解［1-3］.但是对于含有方势垒的一维无限深方势阱的讨论就比较少，本文通过矩阵力学的方法求得其归一化波函数和能级，并且对一种极限情况：即方势垒趋于势垒时粒子的能级进行了讨论.

1 含有势垒的一维无限深方势阱模型及求解

设质量为m的粒子在一个含有方势垒的一维无限深势阱中运动，设势能为：

其中，E为粒子的能量.利用该方程可以求出粒子的能级和波函数.下面就两种情况（）进行求解.

图1 含有势垒的一维无限深方势阱

所以，满足边界条件（2）的势阱波函数的通解可分别写为：

即：

即：

将式（4a）、（4b）、（5a）、（5b）表示为矩阵方程的形式：

方程有非零解的条件是式（6）系数矩阵的行列式等于零，进而可以得到：

其解为：

由此可以求出粒子的能级.

所以粒子满足的波函数为：

由归一化条件，可知：

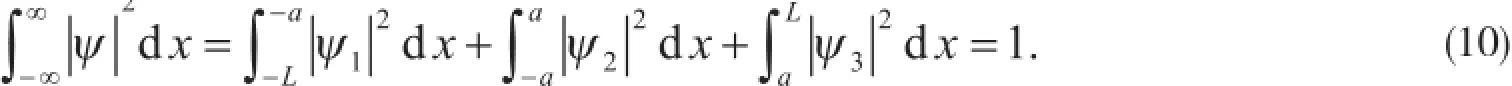
将式（9a）～（9c）代入式（10）可得：

则粒子满足的波函数为：

将式（12a）～（12c）代入式（10），可得：

满足边界条件（2）的势阱波函数的通解可分别写为：

将式（16a）、（16b）、（16c）、（16d）表示为矩阵方程的形式：

方程有非零解的条件是式（17）系数矩阵的行列式等于零，进而可以得到：

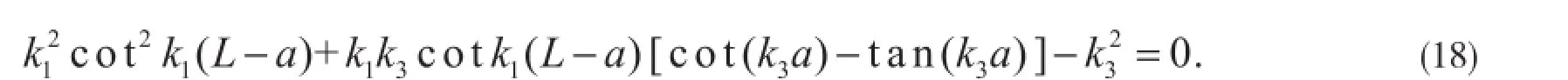
其解为：

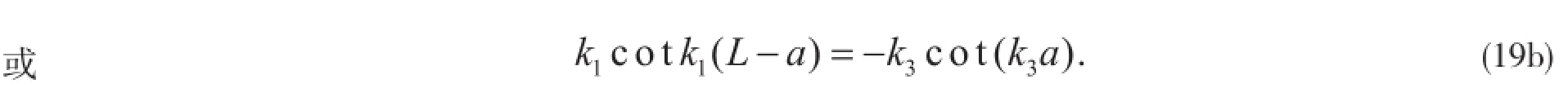
由此可以求出粒子的能级.

所以粒子满足的波函数为：

将式（20a）～（20c）代入式（10）可得：

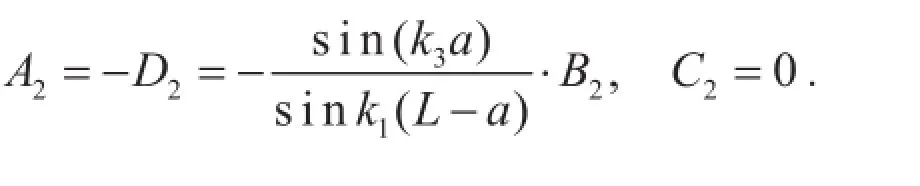
则粒子波函数为：

将式（22a）～（22c）代入式（10）可得：

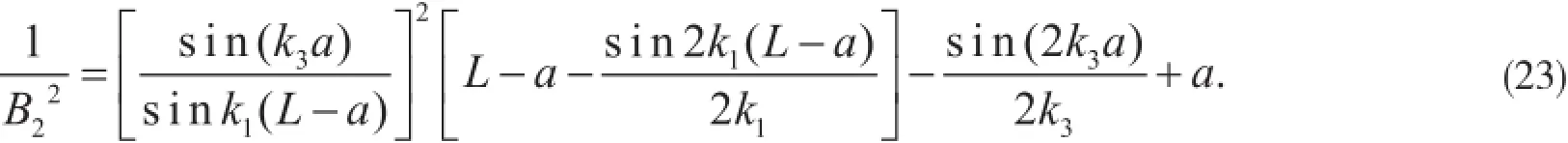
2 讨论一种极限情况

此时，对于式（8a），其右边：

所以式（8a）可变为：

对于式（8b），其右边：

此种情况与无势垒的一维无限深方势阱的能级相同，即相当于此时势垒不起作用.

3 结语

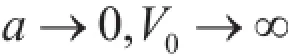
参考文献:

［1］ 周世勋. 量子力学教程［M］.2版.北京：高等教育出版社，2009：26-29.

［2］ 苏汝铿. 量子力学［M］. 上海：复旦大学出版社，1997：37-40.

［3］ 曾谨言. 量子力学：卷Ⅰ［M］. 3版.北京：科学出版社，2001：88-92.

（责任编辑：邵晓军）

中图分类号：O413.1

文献标识码：A

文章编号：1007-5348（2016）02-0001-06

［收稿日期］2015-10-28

［基金项目］韶关学院科研基金项目（314-140640）.

［作者简介］朱昌勇（1985-），男，河南虞城人，韶关学院物理与机电工程学院讲师，硕士；研究方向：理论物理.

A Matrix Solution of One-dimensional Infinite Square Potential Well with Barrier

ZHU Chang-yong
（Institute of Physics and Mechanical & Electrical Engineering， Shaoguan University， Shaoguan 512005， Guangdong， China）

Abstract:Infinite square potential well is an important model of quantum mechanics. With the methods of the matrix mechanics， the normalized wave functions and energy levels are given for the particle in one-dimensional infinite square potential wells with barrier. And the energy level has been discussed when the barrier tends to the barrier.

Key words:infinite potential well； wave functions； barrier