密钥定位耦合有限域余弦变换的图像加密算法

高　峰

(中国太平洋保险(集团)股份有限公司　上海 200234)



密钥定位耦合有限域余弦变换的图像加密算法

高峰

(中国太平洋保险(集团)股份有限公司上海 200234)

摘要图像包含大量的机密信息，在当前网络中传输易被攻击者窃取，而现有的图像加密技术难以兼顾安全性与加密效率。对此，提出有限域余弦变换耦合密钥定位的图像加密算法。首先，将图像分割成多个子块；随后，利用有限域余弦变换处理图像子块，构造中间图像；引入外部密钥，确定中间图像块的位置，再次利用有限域余弦变换，扰乱图像像素，完成图像置乱；迭代Logistic映射，构造像素加密函数，完成扩散。仿真结果表明：与当前图像加密技术相比，该算法具有更高的安全性与加密效率，且该算法的信息熵值更大，能够有效抗击差分攻击。

关键词图像加密密钥空间有限域余弦变换中间图像外部密钥

0引言

随着经济的快速发展，各国之间的博弈也加剧。当前，信息安全已成为各国最为重要的焦点之一，特别是军事领域，涉及到国家安全；在传输中，对其进行保护，能够防止攻击者窃取机密。特别是一些敏感图像，因其所含有的内容特别多，给各部门和研究人员的沟通交流带来巨大便利[1,2]。目前，图像信息安全已演变为各国科研人员与学者的关注焦点。加密技术作为保护信息安全传输的强有力手段，得到了广大学者的研究[3]。但是传统的经典加密算法，如数据加密标准DES、IDEA算法以及RSA算法等，没有考虑到图像具有大数据容量、较高的冗余度等特点，因此将其应用于图像加密会存在较大的不足[4]。为了应对图像安全传输的挑战，国内外学者设计了诸多图像加密技术。Guodong Ye等人[5]为了提高加密机制的安全性，提出了基于波传输与混沌系统的图像加密算法。通过混沌系统生成随机序列，确定波的源点，并获取相应的扩散矩阵，完成图像加密，实验结果显示其算法具有较高的安全性。Xingyuan Wang等人[6]为了提高加密效率，设计了基于混沌映射的图像加密算法。该算法能够并行完成像素置乱与扩散，通过混沌映射产生随机矩阵以置乱图像，再利用置乱图像分块完成像素扩散，仿真数据显示其算法具有较高的加密效率。景党伟等人[7]为了进一步改善加密算法安全度，提出了基于祖冲之算法和DNA编码的图像分组加密方法。利用祖冲之算法产生分组加密结构的密钥流，其次对明文图像信息以及密钥流进行DNA编码，最后利用分组迭代轮数的奇偶性决定明文图像分块模式并基于DNA符号运算的改进Feistel分组结构实现明文图像分组加密，将加密结果进行DNA编码反变换生成最终密文图像，实验结果显示其算法具有很好的抗攻击能力。

尽管当前加密算法能够改善图像信息在网络传输期间被攻击的状况；但是由于这些技术难以兼顾算法安全性与加密效率。

对此，本文提出了有限域余弦变换耦合密钥定位的图像加密算法。首先，将图像分割成多个子块；随后，利用有限域余弦变换处理图像子块，构造中间图像；引入外部密钥，确定中间图像块的位置，再次利用有限域余弦变换，扰乱图像像素；再迭代Logistic映射，构造像素加密函数，完成扩散。

1本文图像加密算法设计

1.1有限域余弦变换

定义1令ζ是有限域GF(p)内的非零元素，其中，p为奇数；则关于ζ的有限域余弦函数模型为：

(1)

其中，x=0,1,2,…,0rd(ζ)，而0rd(ζ)代表ζ的乘法阶。

为了提高算法的复杂度，增加破译难度，本文对式(1)进行改进，得到如下定义。

定义2令ζ是乘法阶为有2N的有限域GF(p)内的元素。则矢量x=[x0,x1,x2,…,xN-1]的有限域余弦变换为X=[X0,X1,X2,…,XN-1],Xk∈GF(p)：

(2)

(3)

式(2)就是本文的有限域余弦变换；且该模型是可逆的：

(4)

依据式(2)可知，矢量x的有限域余弦变换计算可表示为：

X=Cx

(5)

其中，C代表变换矩阵。

通过使用上述矩阵概念，则有限域余弦变换则拓展为二维；则N×N维的矩阵m的2D有限域余弦变换计算模型为：

M=CmC

(6)

可见，由于有限域余弦变换无需对数值进行求舍或者截断操作，使其能够提高算法精度。在本文中，与那些非费马素数的有限域算法相比，有限区域GF(p)能够降低本文算法的计算代价，其中，p为费马素数，如p=2m+1。

考虑一个灰度图像，其像素值范围为[0,255]，为了避免数据损失，本文定义有限域余弦变换中的p≥257。且用于定义该变换的素数数量越大，则需要更多的位来表示图像。考虑这些因素，本文取费马素数p=257来定义有限域余弦变换，其数量ζ=128，则乘法阶数2N=16，则定义如下8×8的变换矩阵C：

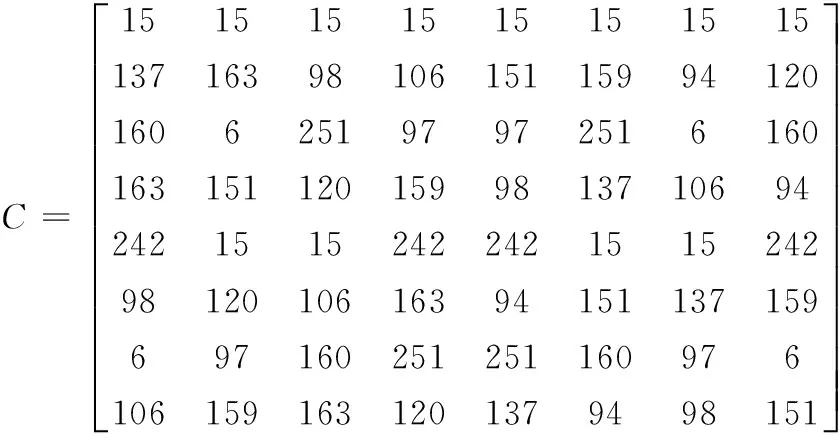
(7)

给定变换矩阵用于8×8灰度图像分块，会产生一个元素值为0～256的矩阵。若变换分块内的任意元素值等于256，则该图像无法被编码。为了消除这种现象，在有限域变换中引入递归操作[8]，直到每个分块的元素值不等于256，该过程见图1所示。

图1　8×8灰度图像分块的有限域余弦变换递归计算

1.2加密算法

本文加密算法流程见图2所示。可见，该算法分为两步：(1) 中间图像的构造；(2) 图像分块的置乱；(3) 像素扩散。

图2　本文图像加密算法流程图

详细过程为：

(1) 将尺寸为M×N的灰度图像分割为8×8子图像Ii,j。每个子图像都是通过图像中的8×8分块中的第i行与第j列来构成。例如，子图像I1,2与I5,4的8×8分块的构造，见图3所示。所得到的8×8分块没有任何叠加。

图3　子图像I1,2与I5,4的8×8分块的构造

(4) 引入外部密钥k，逐个选择中间图像Iinter的分块，再次利用有限域余弦变换，输出置乱图像Ipermutation。

i=(a-1)bz+1,(a-1)bz+2,…,(a-1)bz+bz

(8)

j=βbl+1,βbl+2,…,βbl+bl

(9)

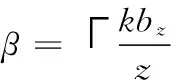
(10)

定义外部密钥σ∈Sn，其中，Sn为n=bl×bz个符号的置乱组合。则该算法的密钥空间为(bl×bz)!。通过从分块中的选择第σ(1)像素，使得置乱密钥σ充当第一个图像分块；在第二个分块中，选择第σ(2)像素，以此类推。通过密钥，定位出相应的分块，通过递归有限域余弦变换，完成置乱。基于密钥的图像分块选择过程见图4所示。

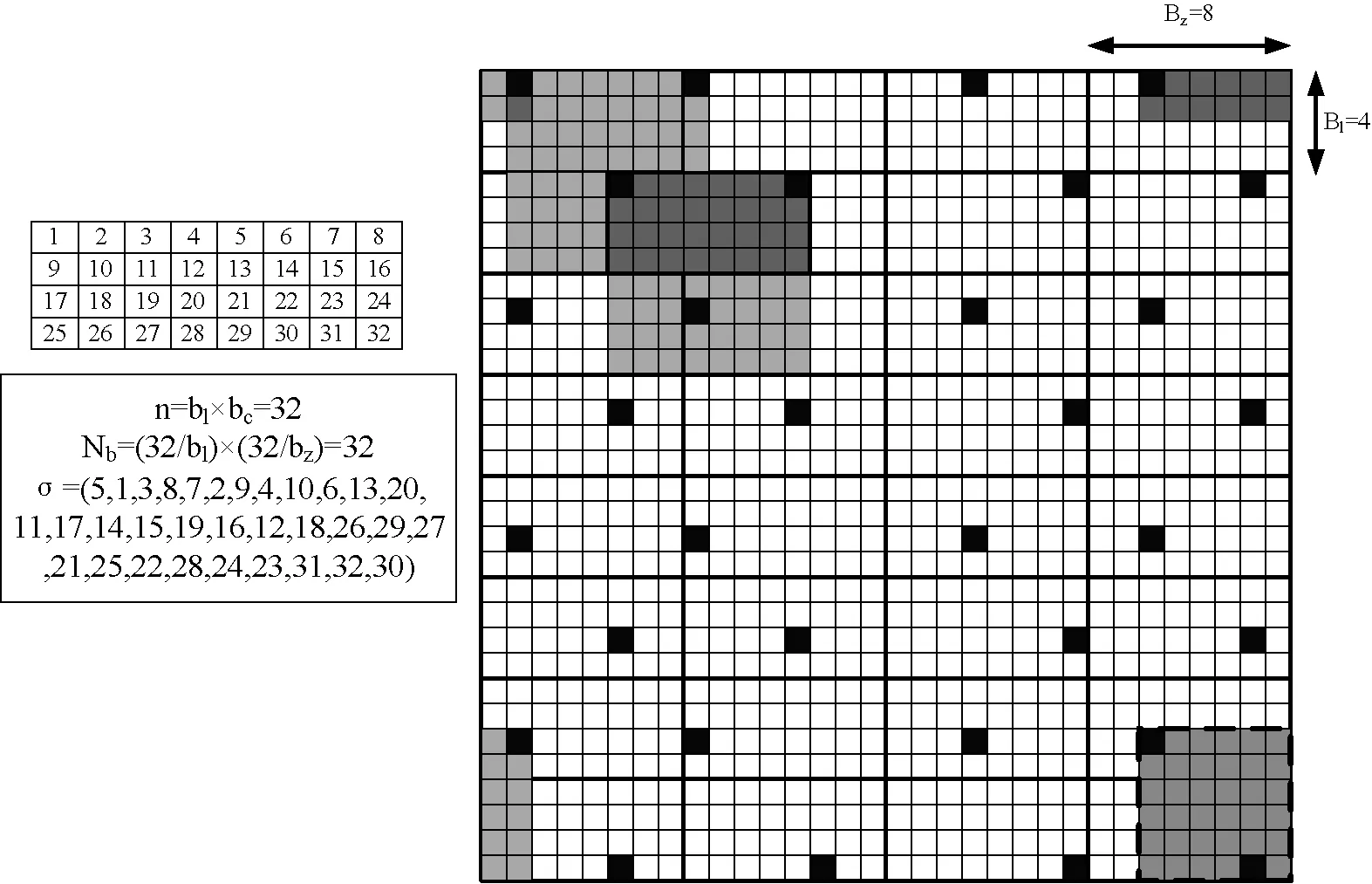
图4　图像分块的选择

(5) 设置好初始值x0，迭代logistic混沌映射，生成伪随机序列x1,x2,x3,…,xM×N：

Xk+1=λXk(1-Xk)

(11)

式中，λ∈[0,4]代表混沌行为控制变量；k=1,2,…,n为迭代数量；X∈[0,1]为变量。

(6) 依据步骤(4)中的置乱图像与x1,x2,x3,…,xM×N，构造像素扩散函数，完成加密：

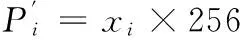
(12)

2实验结果与分析

为了验证所提加密技术的合理性与优异性，在Matlab工具上测试该算法的安全性。与此同时，为了进一步体现该技术的优异性，将：文献[9]- 混沌系统加密、文献[10]-快速图像加密，分别记为A、B算法。整个算法的实验条件为：DELL2.5Hz、双核CPU，8GB的内存，Windows XP系统。定义余弦变换的有限域GF(p)=GF(257)，变换矩阵利用式(6); 在加密期间，中间图像分割为8×4=32个子块，且用于算法的加密密钥σ=(5,1,3,8,7,2,9,4,10,6,13,20,11,17,14,15,19,16,12,18,26,29,27,21,25,22,28,24,23,31,32,30)。

2.1加密效果分析

将尺寸为228×228的灰度军舰图像视为样例，利用本文算法及对照技术对其实施加密，结果见图5(b)-(d)。依据测试结果，在肉眼看来，所提算法与A、B算法都具有较好的保密效果，目标图像的信息被充分扩散，攻击者无法获取任何线索。

图5　三种加密技术的输出密文

为了有效区分本文算法与A、B技术的保密能力，利用信息熵值[10]大小来评估这些技术的优异性：熵值越大，则算法的加密性能越好。其模型为[10]：

(13)

式中，mi为图像像素；M∈[0,256]代表图像灰度水平；P(mi)为mi出现的概率。

按照式(13)与文献[11]的方法，获取图5(b)-(d)的H(m)值。本文以各算法对应的密文H(m)aver均值与最大值H(m)max来对比。计算数据见表1所示。从表中可知，本文加密技术因借助递归有限域余弦变换，充分打乱像素，使其所得到的密文H(m)aver与H(m)max都比较高，与A算法接近，分别为7.9962和7.9987；A算法由于利用了高维混沌系统，使其算法安全性最高，H(m)aver与H(m)max分别为7.9983和7.9994；B算法利用的是1D混沌映射，使其保密性能不佳，H(m)aver与H(m)max分别为7.9937和7.9964。

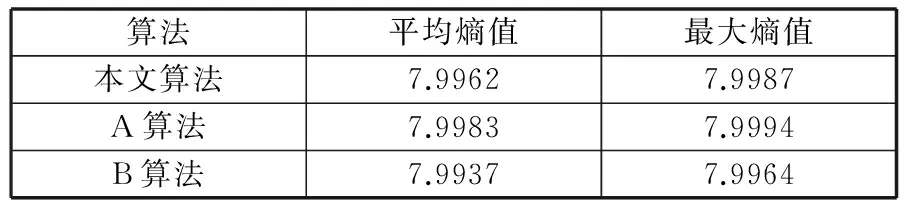
表1　不同加密算法的熵值

2.2抗差分攻击性能分析

差分攻击是当前攻击者最为常用的信息窃取技术之一。为了体现这些算法的抗击差分攻击特性，本文引用NPCR与UACI来体现这三种算法高度安全性[12]：

(14)

(15)

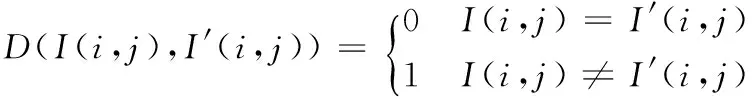
(16)

其中，M×N为密文尺寸；I(i,j)、I′(i,j)均为密文，二者之间只有一个像素差异。

依据式(14)-式(16)，得到三种算法的NPCR值与，UACI值，见图6所示。依图可知，本文算法得到的稳态NPCR、UACI分别为99.572%、33.317%。本文算法的UACI值与NPCR值，非常接近A算法，但比B算法高。

图6　算法的抗差分攻击能力测试

2.3自相关特性分析

若算法能够显著降低图像像素之间的自相关特性，则算法的安全性越高。为了节约成本，本文取水平方向为测试样本。在明文与密文图像中随意择取3000对相邻像素点，估算相关系数[13]rxy：

(17)

图7是明文与密文中的相邻像素的rxy计算结果。根据图像显示，明文中的响铃像素之间具有强烈的自相关特性，其rxy=0.9752，演变为一条对角线，见图7(a)所示；利用所提技术处理后，这种特性被大幅度消除，像素呈现均匀分布态势，rxy=0.0019，见图7(b)所示。

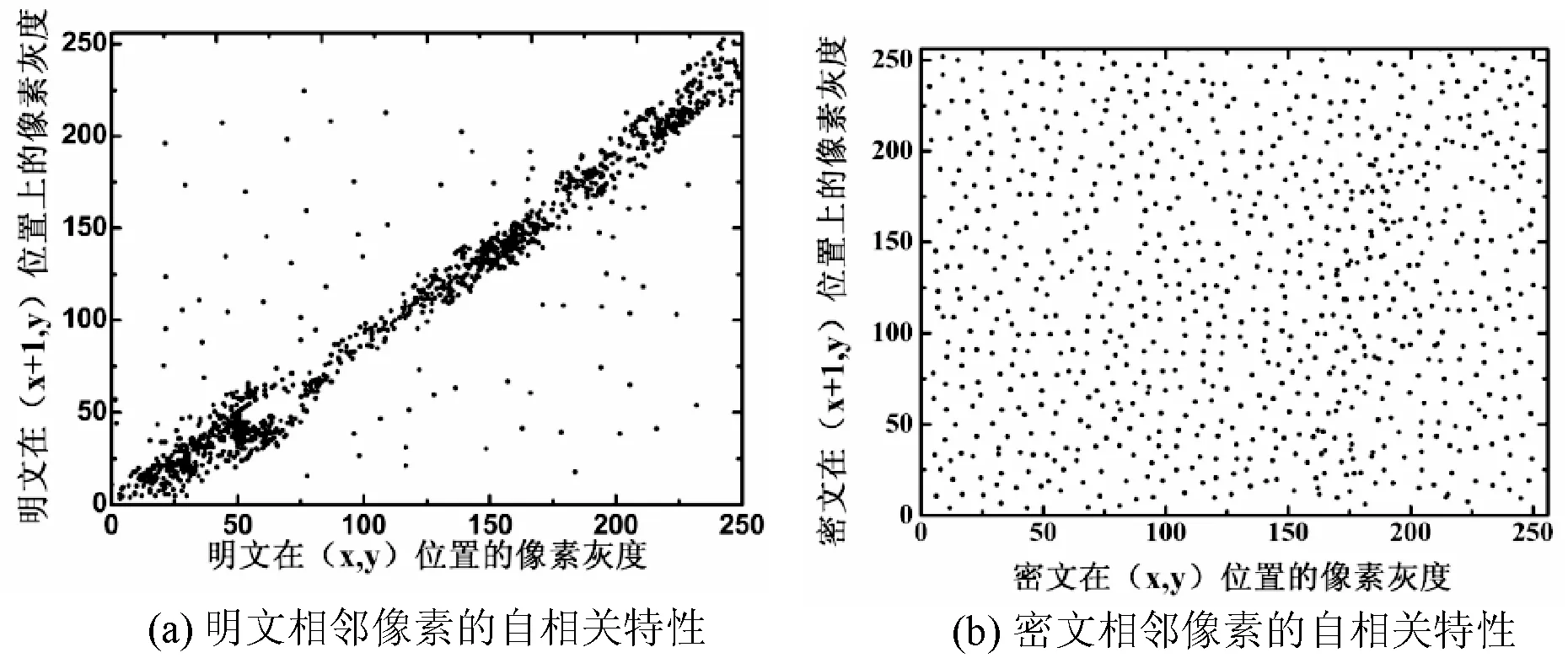
图7　相邻像素的自相关特性测试

2.4加密速度分析

加密算法除了考虑安全性之外，其效率也是非常重要的指标。测试条件与前面相同。采用所提加密技术与A、B算法测试图5(a)。三种算法的时耗分别为：0.05、0.13、0.03 s。可见，本文算法的加密效率与B算法非常接近。主要原因是本文算法是一个分块加密技术，且有限域余弦变换可同步加密这些子块，且去复杂的迭代过程，故提高了算法的加密速度；而A算法使用了高维混沌系统，使其时耗较高；而B算法利用1D混沌映射，算法非常简单，使其加密效率最高。

3结语

为了使算法兼顾高安全性与高效加密效率，确保图像安全传输，本文提出了有限域余弦变换耦合密钥定位的图像加密算法。首先，将图像分割成多个子块；随后，利用有限域余弦变换处理图像子块，构造中间图像；引入外部密钥，确定中间图像块的位置，再次利用有限域余弦变换，扰乱图像像素，完成图像加密。仿真结果表明：与当前图像加密技术相比，本文算法具有更大的密钥空间与更高的加密效率；且该算法能够显著抗击差分攻击。

参考文献

[1] Pedro María Alcover,Juan Suardíaz.A piecewise affine warping algorithm for image rectification in an industrial application for ship hull repair[J].Journal of the Franklin Institute,2013,351(2):763-784.

[2] Sudhir Kumar Chaturvedi,ChanSu Yang.Ship Recognition by Integration of SAR and AIS[J].Journal of Navigation,2012,65(2):323-337.

[3] Yaru Liang,Guoping Liu,Nanrun Zhou.Image encryption combining multiple generating sequences controlled fractional DCT with dependent scrambling and diffusion[J].Journal of Modern Optics,2015,62(4):251-264.

[4] 邓晓衡,廖春龙,朱从旭.像素位置与比特双重置乱的图像混沌加密算法[J].通信学报,2014,35(3):216-223.

[5] Guodong Ye.A block image encryption algorithm based on wave transmission and chaotic systems[J].Nonlinear Dynamics,2014,75(3):417-427.

[6] Xingyuan Wang,Kang Guo.A new image alternate encryption algorithm based on chaotic map[J].Nonlinear Dynamics,2014,76(4):1943-1950.

[7] 景党伟,吴成茂.基于祖冲之算法和DNA编码的图像分组加密方法[J].计算机应用研究,2014,32(8):1334-1340.

[8] Sachin Kumar R K Sharma.Recursive Information Hiding of Secrets by Random Grids[J].Cryptologia,2013,37(2):154-161.

[9] Fatih Özkaynak,Sirma Yavuz.Analysis and improvement of a novel image fusion encryption algorithm based on DNA sequence operation and hyper-chaotic system[J].Nonlinear Dynamics,2014,78(2):1311-1320.

[10] 刘祝华.自适应混沌的并行双向图像加密方案[J].现代电子技术,2014,37(8):119-122.

[11] Zongjie Cao,Yuchen Ge,Jilan Feng.Fast target detection method for high-resolution SAR images based on variance weighted information entropy[J].EURASIP Journal on Advances in Signal Processing,2014,19(1):1-11.

[12] 周伟.基于广义帐篷映射的图像加密算法[D].汕头:汕头大学,2011:30-65.

[13] 董虎胜,陆萍,钟宝江.基于Hénon映射与魔方变换的图像加密算法[J].计算机应用与软件,2014,31(5):291-294.

收稿日期：2015-07-22。高峰，硕士，主研领域：企业信息化与信息安全。

中图分类号TP391

文献标识码A

DOI:10.3969/j.issn.1000-386x.2016.07.071

IMAGE ENCRYPTION ALGORITHM WITH KEY LOCALISATION COUPLING FINITE DOMAIN COSINE TRANSFORM

Gao Feng

(ChinaPacificInsurance(Group)Co.,Ltd.,Shanghai200234,China)

AbstractImages contain a large number of confidential information and are easy to be stolen by the attackers in current network transmission. However existing image encryption technology is difficult to balance both the security and the encryption efficiency. So in this paper we propose an image encryption algorithm with key localisation coupling the finite domain cosine transform. First, we divide the image into multiple sub-blocks; Secondly, we process these image sub-blocks with finite domain cosine transform to construct intermediate image; Finally, we introduce the external key to determine the location of the intermediate image block, and use finite domain cosine transform once again to disturb the pixels of image to complete image scrambling. After that we iterate the Logistic mapping, construct the pixel encryption function, and complete the diffusion. Simulation results show that this algorithm has higher security and encryption efficiency compared with current image encryption techniques, and the information entropy of this algorithm is bigger and is able to fight against differential attacks.

KeywordsImage encryptionKey spaceFinite domain cosine transformIntermediate imageExternal key