基于同层节点集划分的模糊概念格并行构造算法

孙　佳　柴玉梅

(郑州大学信息工程学院　河南 郑州 450001)



基于同层节点集划分的模糊概念格并行构造算法

孙佳柴玉梅

(郑州大学信息工程学院河南 郑州 450001)

摘要形式概念分析理论在诸多计算机领域得到广泛应用。模糊概念格的构造仍是其在应用过程中的一个主要问题。为提高模糊概念格的构造效率，对串行算法进行并行化改造，提出模糊概念格的并行构造算法。该算法对节点进行层次划分，给出了同层节点的定义，得出同层节点构造任务相互独立的重要性质，并引入映射函数简化搜索空间的遍历，提高搜索模糊概念格的效率，并行构造模糊概念格，达到了提高构造效率的目的。实验表明该算法在面对大规模的构造任务时，具有良好的性能。

关键词模糊概念格构造模糊集节点分层并行算法

0引言

形式概念分析FCA(Formal Concept Analysis)由德国学者Wille提出的一种基于形式背景表示形式概念的模型，即概念格[1]。这种概念层次结构是数据分析及规则提取的有效工具，已被广泛应用于文本处理，知识表达，知识挖掘，专家系统等领域[2-6]。但是在许多应用中，大多数信息都是模糊的、复杂的，传统的形式概念分析很难表达这些模糊的、不确定的信息。为解决这个问题，Burusco等人提出了L-模糊形式背景[7]，并将Zadeh的模糊集合理论与形式概念分析相结合，构造模糊形式概念分析FFCA(Fuzzy formal concept analysis)，这一新研究领域[7,8]。在L-模糊形式背景规模较大时，从L-模糊形式背景构造模糊概念格通常会引起组合爆炸，模糊概念格的构造效率是其在应用过程中的一个主要问题。

对基本算法的并行化改造被用来作为提高构造效率的有效途径，多名研究人员通过这种方法取得了并行构造算法的研究成果。在经典概念格方面，文献[9]对形式背景进行划分，运用概念格合并出理论，提出了一种基于子概念格合并的并行构造算法；文献[10]提出并行化Next Closure算法，该算法将形式背景通过字典序划分为不相交的搜索空间，然后由不同线程分别产生概念集合；文献[11]提出了Close By One算法的并行版本，在原始CBO算法思想上进行的并行改造，多个线程并行处理，提前避免产生重复概念，无需进行线程间通信，而且无需进行盲目的空间搜索。这些经典概念格的并行构造算法都是在串行算法基础上改造而来。在模糊概念格方面，目前并行构造算法的研究成果较少。文献[12] 在文献[13] 模糊概念构造算法的基础上设计模糊概念格并行算法。该算法将模糊集合组合空间映射为自然数空间，利用并行计算能力并行构造模糊概念，缺点是它并没有产生格结构，在实际应用中具有一定的局限性。Belohlavek在文献[14]中设计了另一种模糊概念格构造算法，直接构造出L-模糊概念格。本文在文献[14]的基础上，进行并行化改造，设计出一种模糊概念格的并行构造算法。

本文设计的模糊概念格的并行构造算法将模糊概念格进行分层，利用同层节点构造子节点时任务相互独立的重要性质，进行任务分配与结果集成。并引进映射函数简化搜索空间的遍历，提高模糊概念格构造效率。

1相关概念

本节简要介绍所需要的基本概念，对模糊概念格的详细描述见参考文献[8,13]。

模糊形式背景由四元组(X,Y,I,L)表示，其中X为模糊对象集合，Y为模糊属性集合，I为(X,Y)上的二元模糊关系，L为真值集合，取值范围是[0,1]。对于任意的A∈LX，B∈LY，Belohlavek定义了它们之间的模糊伽罗瓦联系：

A↑(y)=∧x∈X(A(x)→I(x,y))

(1)

B↓(x)=∧y∈Y(B(y)→I(x,y))

(2)

其中，可认为是A↑(y)模糊集合A中对象共有属性y的真值度；而B↓(x)认为是对象x拥有模糊属性集合B中所有属性的真值度。二元组(A,B)∈LX×LY满足A↑=B，B↓=A，则称(A,B)为模糊形式背景的一个模糊概念。由模糊概念格的格结构特征，对于其中的每一个模糊概念都称为是一个模糊概念节点，通常简称为节点。模糊概念之间的偏序关系由模糊集合包含关系来确定,对于任意两个模糊概念C1(x1,y1)与C2(x2,y2)，如果x1⊆x2(或y1⊇y2)则有C1 (x1,y1)≤C2 (x2,y2)。模糊形式背景K=(X,Y,I,L)上的所有模糊概念及其上的偏序关系构成一个偏序集(C,≤)，是一个完备格，称之为模糊概念格。

定义1父子节点在模糊概念格的格结构中，模糊概念C1(A1,B1)和C2(A2,B2)，如果C1≤C2且不存在模糊概念C3(A3,B3)C1≤C3≤C2，则称C2为C1的直接父节点，相应的C1称为C2直接子节点。

对于一个模糊概念格，其由全部的模糊概念以及父子关系构成。根据这种结构特点，每个模糊概念在模糊概念格内都具有深度特征。

定义2节点深度在模糊概念格中，模糊概念节点C1(A,B)到最小内涵模糊概念节点C2(X,∅)之间最短路径上有k-1个模糊概念相链接，记模糊概念C1(A,B)的深度为K，记为Dep(C1)=K。

模糊概念格内每个节点都具有唯一深度，由深度可以很好地描述其在模糊概念格内的结构特征。

定理1模糊概念格内每个节点的深度唯一。

证明：任意节点C的深度Dep(C)=K1，根据定义节点C到最小内涵节点之间最短路径链的长度为k1-1；若其深度有多值，假设C的另一深度Dep(C)=K2(K2≠K1)，根据定义此时最短路径链的长度为k2-1。若k2>k1(或k1>k2)，k2-1(或k1-1)的路径长度不是最短，与定义矛盾，故模糊概念格内每个节点的深度唯一。

模糊概念格的结构具有明显的层次性，根据节点深度可以对模糊概念进行层次划分，每个节点都具有相应的层次。

定义3节点层次模糊概念C1(A,B)的深度为k，则称模糊概念C1(A,B)在模糊概念格中层次为k。

推论1在模糊概念格中，每个节点都具有唯一的层次。

证明：节点的深度决定节点的层次，根据定理1，在模糊概念格内每个节点的深度唯一，故可证每个节点具有唯一的层次。

在模糊概念格内，模糊概念具有明显的深度、层次特征，由此也可以更清楚地表示出模糊概念格的层次结构特点。

2串行构造算法

基于对模糊概念格的定义，文献[14]中给出模糊概念串行格构造算法。下面简要介绍计算方法。

(3)

最终B的父节点的集合为：

(4)

B*表示B的父节点集合，具体的证明在参考文献中已有详细描述。结合父节点集合计算方法，模糊概念格的串行构造算法(Fuzzy Lattice算法)具体过程如下：

Step1 初始化F=∅，从最小内涵B=∅开始；

Step3 从父节点集合内选取一个节点E，搜索模糊概念格F判定是否已存在，若存在只需记录父子关系；若不存在将E插入F并生成格结构，且E作为父节点调用式(4)计算其子节点集合N；

Step4 父节点集合内的每个节点递归执行第三步，直到全部计算完毕为止，求出所有的模糊概念并形成格结构。

分析Fuzzy Lattice算法，其从最小内涵开始，由式(4)逐个计算节点的子节点集合，并形成格结构，其时间复杂度为Τ1=O(|X|×|Y|2×|F|),其中|F|为模糊概念格中模糊概念的总数量[14]。在实际应用中，模糊形式背景的规模较大，|X|和|Y|都会增大，模糊概念的数量|F|大规模增大，构造模糊概念格的时间指数倍增加，构造效率低下，此时Fuzzy Lattice算法具有一定的局限性。

进一步分析Fuzzy Lattice算法过程，其逐层计算节点的子节点集合，并构造模糊概念格，且计算每个子节点集合的任务相互独立。此时，独立的计算任务为设计并行构造算法提供了思路，进而由并行算法提高模糊概念格的构造效率，解决其在实际应用中的问题。

3模糊概念格并行构造算法

根据上节Fuzzy Lattice算法，本节对其进行并行化改进，设计出模糊概念格并行构造算法ParaFuLa(Parallel Fuzzy Lattice)。下面详细介绍相关的理论基础和算法。

3.1理论基础

研究模糊概念格的结构知其具有明显的层次性，根据层次性可以对模糊概念进行层次划分，从而更深入地研究模糊概念格的构造特点，设计相应的并行算法，提高构造效率。下面对以上分析结果进行形式化证明。

定义4同层节点两个模糊概念C1和C2具有相同层次，则C1和C2互为同层节点。

命题1同层节点在构造父节点时，任务相互独立。

证明节点在构造父节点时，执行式(4)计算其全部父节点，且同层节点不可比，不存在父子关系，在构造父节点时任务相互独立。

定义5同层节点集在同一模糊概念格内，具有相同层次的模糊概念的集合，称为同层节点集。

同层节点集在构造过程中作为任务集合，可以从任意点进行拆分，作为并行计算的子任务。

定义6子集与分割点同层节点集U中任意两个元素U[n1]和U[n2](0≤n1≤n2≤U.length-1)，在它们之间所有元素的集合称为一个子集，表示为U[n1,n2]，其中n1、n2称为子集的左、右分割点。

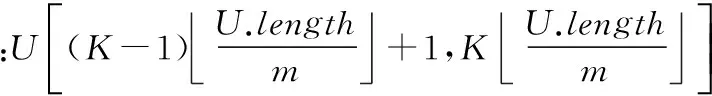
定义7集合U内所有节点的子节点集合的并表示为U*。

例如，U={E1,E2,…，En}，则所有节点的子节点集合的并为E1*∪E2*∪…∪En-1*∪En*，为了便于论述通常由U*来表示，即U*=E1*∪E2*∪…∪En-1*∪En*。

各个并行计算节点获取到子集后，计算子集内每个节点的子节点集合，子集Ui的计算结果表示为Ui*，而同层节点集合U的计算结果表示为U*。各子集计算结果的并应与全集的计算结果相等，命题如下。

命题2同层节点集U拆分成n个子集(U=U1∪U2∪…∪Un-1∪Un)，则U*=U1*∪U2*∪…∪Un-1*∪Un*。

证明：

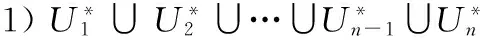
计算子集任务时，各计算节点并行计算，之间不需要通信。完成计算后与主节点(ID=0)通信，将结果发送到主节点处，由主节点集成各个子集的计算结果。模糊概念格内会出现一个子节点拥有多个父节点的情况，故一个子节点可被不同父节点多次计算出来，在结果集成时，每个子节点都需要搜索模糊概念格F以判断是否已存在。

在计算过程中，需要多次搜索模糊概念格F，因此模糊概念格F的搜索效率直接影响算法的效率。模糊概念格F的搜索空间的表示与搜索方法可利用已有的结论。根据文献[12]，F的搜索空间与一维n位‖L‖进制数集合按大小自然排序同序，而任意进制数与十进制数之间存在转换关系，故一维n位‖L‖进制数可以转换为十进制数，映射函数ρ为：

ρ(s)=m1‖L‖n-1+m2‖L‖n-2+…+mn-1‖L‖1+mn‖L‖0

(5)

通过式(5)可将F的搜索空间内模糊概念映射为自然数，在集成计算结果时，直接查询自然数来确定生产的节点是否在F内存在，减少访问F消耗的时间。详细论述请参考文献[9]。

在集成计算结果时，子节点被不同父节点多次计算生成，具有一定的冗余，但由于建立模糊概念格的格结构，需要所有节点的父子关系，因此不可避免。

3.2算法描述

由上文理论分析，同层节点的构造任务相互独立，同层节点集U根据计算节点个数拆分为多个子集，每个计算节点完成一个子集的计算任务，结果U*在主节点处集成，并更新U(U=U*)作为新的同层节点集，递归重复计算，直到全部计算完毕形成模糊概念格。模糊概念格的并行构造算法描述如下：

算法Parallel Fuzzy Lattice

输入模糊形式背景K；

计算节点个数m

输出模糊概念格F

1. F=(，U=(，B=(↓↑；

//式(4)

3. Parallel Generate From(F,U,ID=0);

4. Return F

ParaFuLa算法的主程序主要负责初始化程序入口，具体的计算由函数ParallelGenerateFrom来完成。函数ParallelGenerateFrom描述如下：

函数ParallelGenerateFrom (K,U,ID)

输入模糊形式背景K；

集合U；

计算节点ID

输出模糊概念格F

1. While(U≠∅)

2. If (ID = = 0)

3. // ID=0,负责任务分配与结果集成

4. For ID=1 to m

5. Receive(ID,U*)

6. (U,F)=Merge(U*)

8. n2= n2>U.length-1? (U.length-1)∶n2

9. Send(K,U[n1,n2],ID)

10. End for

11. Else

12. // ID=1…m，负责子任务，计算结果发送到ID=0处

13. Receive(K,U[n1,n2])

14. U*=Generate From(K,U);

15. Send(ID=0,U*);

16. End if

17. End while

函数ParallelGenerateFrom是算法的主体，第2-11行是主节点(ID=0)执行部分，主要负责：1)任务分配，由定义6，将同层节点集U拆分成m个子集，再根据ID分配子集； 2)结果集成，主节点接收其它计算节点(ID=1…m)的计算结果，执行函数Merge集成各个子集的计算结果，与此同时更新同层节点集U，作为新一轮的任务集合。第12-15行是其他计算节点(ID=1…m)执行部分，每个计算节点负责一个子集，执行函数GenerateFrom计算子集任务，结果发送到主节点处集成。

函数GenerateFrom (K,U)

输入模糊形式背景K；

集合U

输出结果集U*

1. If(U≠()

2. For each E∈U && E≠Y

3. U*=U*∪E*

4. For each D∈ E*

5. //记录偏序关系

6. Add E to D*

7. End for

8. End If

9. Return U*

函数GenerateFrom的功能是计算子集任务。计算子集U内每个节点的子节点集合，并在计算过程中记录偏序关系，计算结果形成U*作为函数的返回值。

函数Merge (U*)

输入结果集U*

输出更新集合U，更新F

1. For each E∈U*

2. n=ρ(E)

//定义7

3. If F. flag[n]=false

4. //为新生成节点加入F，否则只记录偏序关系

5. F∪{E,E*,E*};

6. Else add E to F[n].element*

7. End if

9. Add E to U

10. End if

11. Return

函数Merge负责集成子集的计算结果并更新U。对于子集的计算结果U*，由式(5)的映射函数将子节点转化为自然数，进而在F内快速查询，若不存在，为新生成节点加入F；若存在，则只需记录相应的偏序关系。与此同时，U*内的子节点逐个加入U，并避免重复,U完成更新后作为新的同层节点集，拆分成子集进行任务分配，重复执行直至模糊概念格构造完毕。

3.3算法分析

对于以上描述ParaFuLa算法的正确性可通过其构造出的模糊概念格是否同构予以证明。

定理2并行算法ParaFuLa构造的模糊概念格与原串行算法构造出的模糊概念格同构。

证明：(1) 最小内涵节点同时被两种算法构造出来。

(2) 对于每一个由原算法构造出的节点(AK,BK)，在模糊概念格中由偏序关系存在(A,φ)≥(A1,B1)≥…≥(AK-1,BK-1)≥(AK,BK)。若(AK,BK)为(A,φ)的直接父节点，则在并行算法中必定会生成；若(AK,BK)不是(A,φ)的直接父节点，但存在一条链接(A1,B1)≥…≥(AK-1,BK-1)，其中必有(AK,BK)的父节点，由并行算法可知(AK,BK)必由其父节点计算生成，故(AK,BK)必定也存在于并行构造算法构造的模糊概念格内。

(3) 因为并行算法在每个子任务上执行相同的串行算法，所以并行算法产生的节点也必定存在于串行算法构造的模糊概念格内。

由定理2的证明即可知，本文提出的模糊概念格并行构造算法能够正确地构造出模糊概念格。

其次，分析算法的时间复杂度。

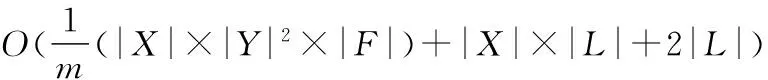
证明：(1)各个并行计算节点在并行执行GenerateFrom函数时，由公式(4)计算子节点集合，需要进行闭包运算和属性集的遍历，计算子节点集合的时间复杂度为O(|X|×|Y|2×|F|)。

(2) 在结果集成时遍历模糊概念格，由式(5)模糊概念格F的搜索空间表示为Y的幂集LY，映射函数ρ将任意模糊概念转换为十进制数，其时间复杂度为O(|X|×|L|)[12]。

(3) 通信量主要为各个并行计算节点与主节点间的通信，由模糊概念的数量和生成次数决定。最坏情况下，任意节点是其下层所有节点的子节点，在构造过程中被下层每个节点重复生成一次，此时完整概念格在构造过程中通信量的时间复杂度为O(2|F|)。

(4) 作为并行算法ParaFuLa算法的时间复杂度由各个计算节点的复杂度决定，主体部分负责任务分配与结果集成。构造模糊概念格由m个计算节点执行GenerateFrom函数，由(1)、(2)和(3)分析，ParaFuLa算法的时间复杂度为：

由以上时间复杂度的分析，ParaFuLa算法利用并行计算方法，在一定程度上提高了模糊概念格的构造效率。

4实验实例

如表1所示模糊形式背景，该模糊形式背景具有4个对象，5个属性。设此时计算节点个数为4，ID等于0为主节点，负责任务分配与结果集成，其它节点计算子任务。

表1　模糊形式背景K

由ParaFuLa算法构造出的模糊格如图1所示，其过程为:

(1) 由程序入口进行闭包运算，得到C1，再由C1计算出其全部子节点集合为U={C2，C3}，记录偏序关系。此时C2和C3为同层节点集。

(2) 此时由定义6对同层节点集U进行拆分，主节点将C2分配给1号(ID=1)计算节点，计算子节点集合为{C4}，C3分配给2号计算节点，计算子节点集合为{C5}，此时集合较小3号计算节点空闲。主节点集成结果为{C4，C5}，更新U={C4，C5}，并记录偏序关系。

(3) 主节点再次对U划分并进行任务分配，1号计算节点计算出{C4}子节点集合{C6，C7，C8}，2号计算节点计算出{C5}子节点集合{C9}，然后主节点集成结果并更新U={C6，C7，C8，C9}，并记录偏序关系。

(4) 由定义6再次对U划分，主节点将{C6}分配给1号计算节点，{C7}分配给2号计算节点，{C8，C9}分配给3号计算节点。各个计算节点计算完毕，主节点集成结果为U={C10，C11，C12，C13}，并记录偏序关系。

(5) 主节点继续进行任务分配，{C10}分配给1号计算节点，{C11}分配给2号计算节点，{C12，C13}分配给3号计算节点，主节点集成结果为U={C14，C15 }，并记录偏序关系。

(6) 主节点将同层节点集{C14，C15 }划分，{C14}分配给1号计算节点，{C15}分配给2号计算节点，主节点集成结果U={C16}，并记录偏序关系。

(7) 此时U={C16}，主节点将{C16}分配给1号计算节点，C16为内涵最大节点，计算得其子节点为空，主节点集成结果U=∅，此时算法结束。

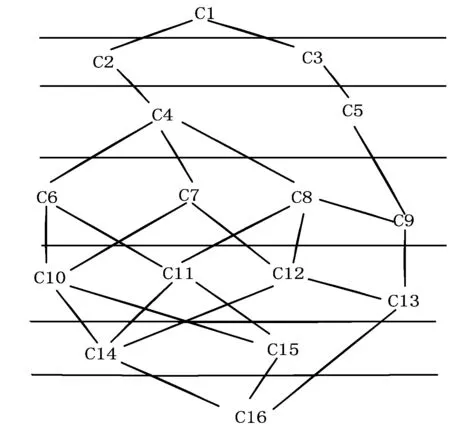
图1　K生成的模糊概念格

图1中同层模糊概念节点由横线标示，同层模糊概念节点任务独立例如同层节点集{C4，C5}和同层节点集{C6，C7，C8，C9}，它们由主节点分分配给不同的计算节点，进行并行计算，且在计算过程中记录偏序关系，最终形成格结构。

为了验证本文提出的并行算法的性能，通过Java编程语言和MPJ平台实现本文所涉及的算法，实验时，程序运行在Intel Xeon 8 Core 多核单处理器计算环境上。首先，以加速比来度量该并行算法的性能，即在相同数据集相同精度下ParaFuLa算法相对于文献[14]Fuzzy Lattice算法构造模糊概念格效率提升程度，实验结果如图2所示。真值集合L 精度分别设置为L3、 L5、L11、L101，4种不同精度，并在不同计算节点数目上进行试验。在L3={0,0.5,1}精度时，计算任务较少，由于在计算过程需要任务分配，结果汇总等额外消耗，使得并行算法的效益无法显现，出现以上结果。精度L5={0,0.25,0.5,0.75,1}时，加速比随节点数正比例增加，而后保持在4左右，精度L11={0,0.1,0.2,…,1}时加速比随节点数小幅增加；精度为L101={0,0.01,0.02,…,0.99,1}时，任务规模增大，加速比随节点数正比例增加，并行算法的效益远大于额外消耗，说明在较大规模模糊概念格构造任务时，并行算法具有良好的性能。

图2　不同节点下的加速比

本文ParaFuLa算法和文献[12] Parallel Fuzzy Next Closure算法的比较实验结果如图3所示。由图3可知在不管是L3精度还是L5精度下，Parallel Fuzzy Next Closure算法的效果都比本文ParaFuLa算法要好，分析原因是本文ParaFuLa算法产生格结构，在构造模糊概念格时需要记录模糊概念节点之间的偏序关系，从而产生通信和部分重复计算；而Parallel Fuzzy Next Closure算法只是产生模糊概念全集，并不产生格结构，没有计算模糊概念之间偏序关系。故由以上原因产生该实验结果。

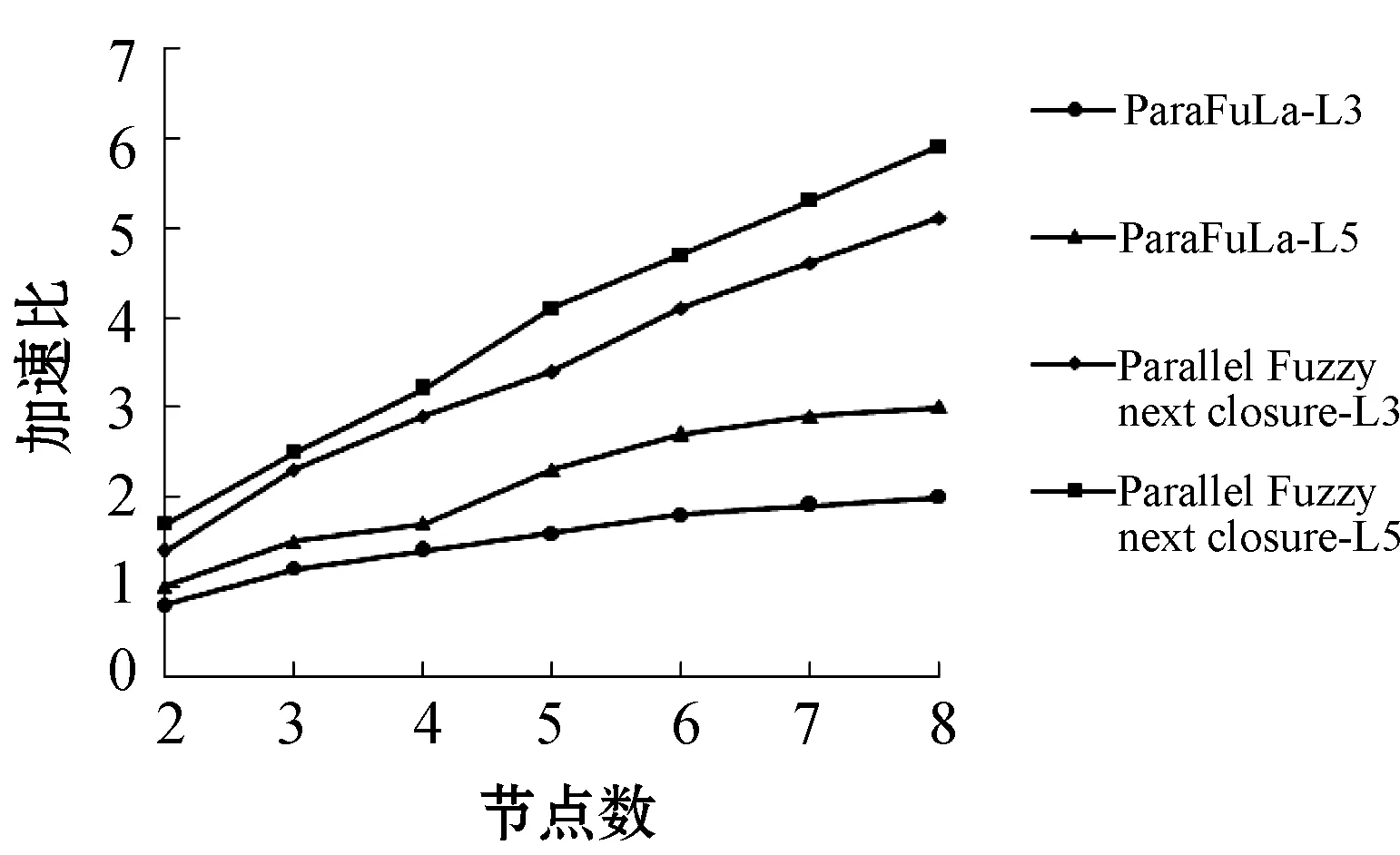
图3　L3和L5精度下的加速比比较

ParaFuLa算法对模糊概念进行层次划分，同层节点集拆分为多个子集，多个计算节点同时参与计算，充分发挥并行计算的优势。但在算法过程中，由于需要记录偏序关系并产生格结构，计算冗余和通信都是有待改进的地方。

5结语

模糊概念格是一种有效的数据挖掘工具，已被广泛应用于模糊数据分析、规则提前等领域。基于模糊概念格的应用都需要以其构造为基础，面对构造效率问题，并行算法是解决构造效率问题的有效办法。本文提出了一种模糊概念格并行构造算法。该算法从同层节点的构造任务相互独立出发，拆分同层节点集，子集任务并行进行，结果集成时简化搜索空间的遍历，使得充分利用并行计算的优点，并行构造模糊概念格。下一步将继续研究模糊形式概念分析技术及其在数据挖掘等领域的应用。

参考文献

[1] Ganter B,Wille R.Formal Concept Analysis:Mathematical Foundations[M].Springer Verlag,Berlin,1999.

[2] 柴玉梅,王春丽,王黎明.基于频繁项集的互补替代关系挖掘算法[J].模式识别与人工智能,2012,25(1):157-165.

[3] 柴玉梅,张卓,王黎明.基于频繁概念直乘分布的全局闭频繁项集挖掘算法[J].计算机学报,2012,35(5):990-1001.

[4] 王黎明，张卓.基于iceberg概念格并置集成的闭频繁项集挖掘算法[J].计算机研究与发展,2007,44(7):1184-1190.

[5] 张卓,李石君,张乃洲，等.基于格空间的受限Deep Web数据抽取算法[J].模式识别与人工智能,2011,24(1):130-137.

[6] Zhang Z,Du J,Wang L.Formal concept analysis approach for data extraction from a limited deep web database[J].Journal of Intelligent Information Systems,2013,41(2):211-234.

[7] Burusco A,Fuentes-Gonzalez R.The Study of the L-Fuzzy Concept Lattice[J].Math ware & Soft Computer,1994,1(3):209-218.

[8] Belohlavek R.What is a fuzzy concept lattice? II[M]//Rough Sets,Fuzzy Sets,Data Mining and Granular Computing.Springer Berlin Heidelberg,2011:19-26.

[9] 智慧来,智东杰,刘宗田,等.概念格合并原理与算法[J].电子学报,2010,38(2):455-459.

[10] Fu H,Nguifo E M.A parallel algorithm to generate formal concepts for large data[M]//Concept Lattices.Springer Berlin Heidelberg,2004:394-401.

[11] Krajca P,Outrata J,Vychodil V.Parallel recursive algorithm for FCA[C]//CLA.2008,2008:71-82.

[12] 张卓,柴玉梅,王黎明,等.模糊形式概念并行构造算法[J].模式识别与人工智能,2013,26(3):260-269.

[13] Belohlavek R.Algorithms for fuzzy concept lattices[C]//Proc.Fourth Int.Conf.on Recent Advances in Soft Computing.Nottingham,United Kingdom.2002:200-205.

[14] Belohlavek R,De Baets B,Outrata J,et al.Computing the lattice of all fixpoints of a fuzzy closure operator[J].Fuzzy Systems,IEEE Transactions on,2010,18(3):546-557.

收稿日期：2015-03-09。孙佳，硕士，主研领域：形式概念分析、数据挖掘。柴玉梅，教授。

中图分类号TP311

文献标识码A

DOI:10.3969/j.issn.1000-386x.2016.07.060

PARALLEL CONSTRUCTION ALGORITHM FOR FUZZY CONCEPT LATTICE BASED ON PARTITIONING OF SAME-LAYER NODES SET

Sun JiaChai Yumei

(SchoolofInformationEngineering,ZhengzhouUniversity,Zhengzhou450001,Henan,China)

AbstractThe theory of formal concept analysis (FCA) is extensively applied in various computer fields.Constructing fuzzy concept lattice is still a major issue in its application process.In order to improve the efficiency of fuzzy concept lattice construction,we presented a parallel construction algorithm for fuzzy concepts lattice by reforming the serial construction algorithm to the parallelised one.The proposed algorithm stratifies the nodes,by defining the concept of same-layer nodes,we derived the important nature of the same-layer nodes that their construction tasks are independent each other,and the introduction of mapping function simplifies the search space traversal,the efficiency of searching fuzzy concept lattice is thus improved.The parallel construction of fuzzy concept lattice achieves the goal of improving the construction efficiency.Experiments show that the algorithm has good performance when facing with the large scale construction tasks.

KeywordsFuzzy concept lattice constructionFuzzy setNodes stratificationParallel algorithm