基于迭代重加权的广义总变分超分辨率重建

周　芹　马志强　单　勇

(空军工程大学信息与导航学院　陕西 西安 710077)



基于迭代重加权的广义总变分超分辨率重建

周芹马志强单勇

(空军工程大学信息与导航学院陕西 西安 710077)

摘要由于传统超分辨率重建算法在模糊和噪声严重的情况下不能有效地抑制图像中的噪声，提出基于迭代重加权范数的广义总变分超分辨率重建算法。该算法采用迭代重加权的数据保真项和正则项构造广义总变分的代价函数，并采用预处理共轭梯度法对其进行优化,能够有效地抑制噪声的产生。实验证明，该算法在去除噪声的同时，能够很好地保持图像的细节信息，有很好的视觉效果。

关键词图像超分辨率广义总变分迭代重加权预处理共轭梯度去噪

0引言

图像超分辨率SR(Super Resolution)是指从多幅低分辨率LR(Low Resolution)图像获得一幅或多幅清晰的高分辨率HR(High Resolution)图像的重建技术。如果将图像的退化模型看成是正问题，那么超分辨率重建问题实际上是一个反问题；又由于噪声的不确定性和低分辨率图像帧数的不足，使得超分辨率重建也是个病态问题。为了解决超分辨率重建算法的病态反问题，引入了正则项以便约束待估计的高分辨率图像的解空间，此方法称为正则化方法。经典的正则化超分辨率重建算法主要有Tikhonov正则化[1]、总变分TV(Total Variation)正则化[2,3]、双边总变分BTV(Bilateral Total Variation)正则化[4-7]和最近提出的总广义变分正则化TGV(Total Generalized Variation)正则化[8,9]。一个典型的重构过程包括了图像配准、高分辨率插值、消除模糊噪声等后期处理过程[10]。

观测到的低分辨率图像在噪声比较大，模糊比较严重的情况下，传统超分辨率重建算法不能很好地抑制噪声。而文献[11]表明迭代重加权范数在去噪和去卷积方面有很好的效果。因此，本文将迭代重加权范数应用于超分辨率重建中，从而提出了基于迭代重加权[11]的超分辨率重建算法。该算法考虑了每帧低分辨率图像的配准误差存在差异，从而对数据保真项采用加权处理。同时，考虑了同一帧低分辨率图像中当前像素的周围像素点对其贡献不同，对正则项也采用加权处理，并利用迭代重加权方法和预处理共轭梯度法对代价函数进行优化求解。

1基础知识

图像观测模型可以描述为景物的高分辨率图像X经过降质(大气扰动变形、光学模糊、镜头下采样以及噪声污染)后，最终得到N帧低分辨率图像Yk,{k∈[1,N]}的过程。因此，观测模型用矩阵形式表示如下：

Yk=DkBkFkX+Nk

(1)

式中，Dk是下采样矩阵；Bk是系统的模糊矩阵；Fk是运动矩阵，可通过图像配准求得。Nk是噪声矩阵。

将其简化可得：

Y=HX+N

(2)

由于模糊、噪声等退化因素的影响或LR图像数量的不足，导致超分辨率图像重建方法是一个具有病态特性的反问题。为了克服病态特性，需要引入正则项进行约束，从而稳定解并加速算法的收敛性。因此典型的超分辨率代价函数可用极小值问题来表示：

(3)

式中，第一项是数据保真项，衡量重建的高分辨率图像经过降质后得到的LR图像与观测到的LR图像的一致性；第二项是正则项，以便约束解的唯一性和稳定性，λ表示正则化参数，主要用于平衡数据保真项与正则项。p、q表示范数,当p=1、q=1时，式(3)相当于L1总变分的代价函数，简记为L1TV；当p=2、q=1时，式(3)相当于L2总变分的代价函数，简记为L2TV。DuX和DvX分别表示图像X在像素点的水平方向和垂直方向的一阶导数。

2基于迭代重加权的超分辨率重建

2.1迭代重加权范数

迭代重加权范数IRN(Iteratively Reweighted Norm)在文献[11]中首次被提出用去噪和去卷积，其定义为：用加权的L2范数等价代替p范数和q范数。

迭代重加权范数是与迭代重加权最小二乘法[12]IRLS(Iteratively Reweighted Least Squares)紧密相关的。IRLS算法采用一个迭代过程求解一系列加权最小二乘问题，并在每一步迭代中按照一定的规则对权系数进行调整，使其逐步逼近最优拉格朗日乘子。IRLS最小化p范数如下：

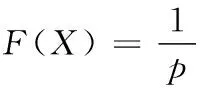
(4)

其中，HX-Y表示配准误差，即估计出的高分辨率图像经过降质后得到的低分辨率图像与观测到的低分辨率图像之间的误差。

迭代重加权范数是指当p<2时，采用迭代的方式，用自适应加权的L2范数逼近最优解。在第k次迭代时，解X(k)是下式的最小解：

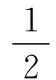
(5)

式中，权重矩阵W(k)1/2= diag(|HX(k)-Y|p-2)，其物理意义是各帧的权重矩阵随配准误差的不同而改变，当配准误差HX-Y较大时，选择较小的权重系数。反之，选择较大的权重系数。

对式(5)求导并令其为0，可得迭代公式为：

X(k+1)=(HTW(k)H)-1HTW(k)Y

(6)

以上分析表明，迭代重加权范数可以利用对权重的调整逐步逼近目标函数的全局最优解。

2.2数据保真项的广义形式

为了采用迭代重加权范数的思想，即用加权的L2范数代替p范数，定义数据保真项为一个二次函数：

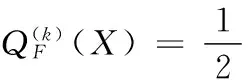
(7)

式中，第二项F(X)的形式如式(4),其中的X(k)是一个常数，表示函数在当前迭代的最优解;并且：

(8)

(9)

2.3正则项的广义形式

为了采用迭代重加权范数的思想，即用加权的L2范数代替q范数，定义正则项为一个二次函数：

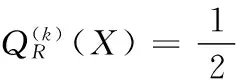
(10)

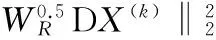
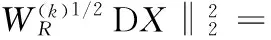
(11)

(12)

(13)

式(11)的推导可参考文献[11]，表示权重系数与像素点的梯度成反比关系，即当边缘处的梯度较大时，采用较小的权重系数以便保留图像的边缘信息；当平坦区域的梯度较小时，采用较大的权重系数以便平滑噪声，从而达到保持图像细节信息的同时能够去除噪声。式(13)表示：当像素点的梯度(DuX(k))2+(DvX(k))2小于阈值εR时，可将权值系数设置为0，即对于正则项而言，梯度很小以至于接近0是被允许的。此时的正则项对迭代没有贡献量，而只取决于前次迭代和当前迭代的保真项。

2.4代价函数及其优化求解

根据以上分析，超分辨率重建模型——广义总变分的代价函数可表示为：

(14)

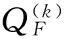
(15)

对于上式可采用预处理共轭梯度法[13]PCG(Preconditioned Conjugate Gradient)对其进行求解，而其中的阈值εF和εR的自适应选取在下文介绍。本文算法步骤如下：

1) 选择低分辨率参考帧，对图像进行Lucas-Canada光流法配准；

2) 对低分辨率参考帧进行插值得到初始高分辨率图像X(0);

5) 如果达到最大迭代次数，则停止迭代，得到的解即为重建的高分辨率图像，否则返回步骤4。

2.5阈值的自适应选取

重建图像质量的优劣取决于权重矩阵的值，而权重矩阵的值与阈值εF和εR的选取是密不可分的。若阈值选取过小，那么迭代次数会增多，从而导致程序运行时间长，效果不明显；若阈值选取过大，那么重建结果不能很好的保持图像的边缘细节信息，导致重建图像质量较差，所以选取合适的阈值对于重建图像质量而言是至关重要的。由式(8)和式(11)可知，阈值是与第k次迭代的解X(k)有关，所以，阈值的选取应随着迭代次数的不同而自适应的改变。

本文首先计算当前迭代过程中重建的高分辨率图像X(k)的累积直方图，通过噪声占有特定的百分比来确定阈值的自适应选取。对于εF，需要确定当前迭代中配准误差的累积直方图，即hF=hist(HX(k)-Y),再计算hF的固定百分比作为阈值εF的值。同样，对于εR，需要确定当前迭代中估计的高分辨率图像的梯度值的累积直方图，即hR=hist(|(DuX(k))2+(DvX(k))2|)q/2，再计算hR的固定百分比作为阈值εR的值。一般地，数据保真项和正则项对应的百分比应该分别低于5%和1%，从而提高重建图像的质量和去噪性能。

3实验与结果分析

为了验证本文的算法的鲁棒性和有效性，在Windows XP平台，Matlab 7.0.1环境下将本文算法与Tikhonov正则化方法以及文献[3]中的L2TV算法作比较。Tikhonov算法非常经典，经常用作对比算法，下面简称TK算法。而文献[3]中的L2TV算法是本文算法在取p=2、q=2时的特殊形式，用以比较本文算法的优越性，之所以选择L2范数，是因为L2范数对高斯噪声的去除性能优于L1范数。采用峰值信噪比PSNR(Peak Signal to Noise Ratio)和归一化的均方误差NMSE(Normalized Mean Square Error)作为质量评价标准，PSNR和NMSE的公式如下：

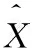
实验采用尺寸为383×383的peppers图像和512×512的Goldhill图像作为原始图像。将图像经过随机平移，用半径为3.2的圆形区域进行高斯模糊(方差为5)，再以因子2对其下采样。最后加入方差为0.01的高斯噪声产生4幅低分辨率图像，将图像的灰度值规整到[0,1]，利用这4幅低分辨率图像序列进行超分辨率重建。本文算法选择的参数为p=2、q=1,自适应阈值εF中选取的百分比为0.05，自适应阈值εR中选取的百分比为0.1，迭代次数为3。

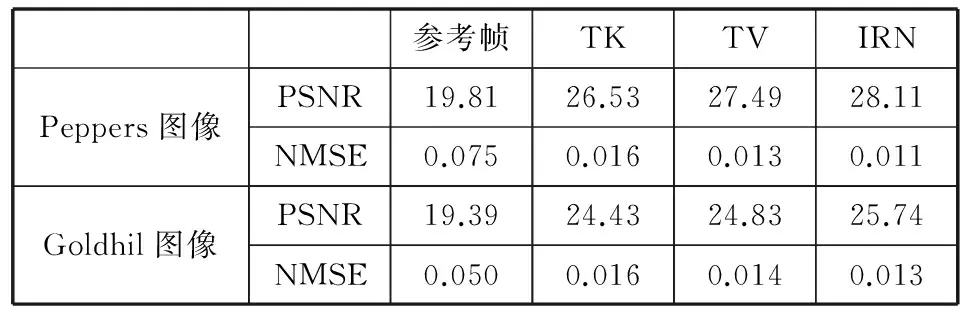
几种不同算法的peppers图像和Goldhill图像得到的重建结果如图1和图2所示。其中(a)表示参考帧，(b)、(c)、(d)分别表示TK算法、TV算法和本文算法的重建结果。从图1和图2可以直观地看出本文算法的去除噪声性能明显优于TK算法和TV算法。重建结果的PSNR和NMSE的值如表1所示，本文算法的峰值信噪比明显高于前两种方法，归一化的均方误差比前两种算法都小，从定量上表明本文算法保留了更多的图像细节信息，进一步反映了本文算法的优越性。

图1　不同算法的peppers图像的超分辨率重建结果

图2　不同算法的Goldhill图像的超分辨率重建结果

参考帧TKTVIRNPeppers图像PSNR19.8126.5327.4928.11NMSE0.0750.0160.0130.011Goldhil图像PSNR19.3924.4324.8325.74NMSE0.0500.0160.0140.013

4结语

本文针对在噪声较大、模糊比较严重的情况下，传统的图像超分辨率重建不能很好兼顾抑制噪声和保持图像细节信息的不足，提出了基于迭代重加权范数的广义总变分超分辨率重建算法。该算法在分析了迭代重加权范数原理的基础上，将迭代重加权思想分别应用于数据保真项和正则项，从而定义了它们的广义形式，构造了广义总变分的代价函数，并对其中的权重及其阈值进行自适应调整，利用预处理共轭梯度对其迭代，确定最优解。结果表明，本文算法不仅有优越的去噪性能，还能保持更多的图像细节信息。

参考文献

[1] 商俊国,焦斌亮.多帧图像的Tikhonov正则化重建算法研究[J].计算机应用研究,2011,28(2):785-787,791.

[2] Rudin L,Osher S,Fatemi E.Nonlinear total variation based noise removal algorithms[J].Physical Review D,1992,60(1-4):259-268.

[3] 占美全,邓志良.基于L1范数的总变分正则化超分辨率图像重建[J].科学技术与工程,2010,10(28):6903-6906.

[4] Farsiu S,Robinson M D.Fast and Robust Multiframe Super Resolution[J].IEEE Transactions on Image Processing,2004,13(10):1327-1344.

[5] 安耀祖,陆耀,赵红.一种自适应正则化的图像超分辨率算法[J].自动化学报,2012,38(4):601-608.

[6] 杨欣,周大可,费树民.基于自适应双边全变差的图像超分辨率重建[J].计算机研究与发展,2012,49(12):2696-2702.

[7] 蒋建国,董艳春.边缘增强型非局部模型超分辨率重建算法[J].中国图象图形学报,2011,16(10):1772-1778.

[8] Bredies K,Kunisch K,Pock T.Total generalized variation[J].SIAM J Imaging Sciences,2010,3(3):492-526.

[9] Knoll F,Bredies K,Pock T,et al.Second order total generalized variation(TGV)for MRI[J].Magnetic Resonance in Medicine,2011,65(2):480-491.

[10] 李家德,张叶,贾平.采用非局部均值的超分辨率重构[J].光学精密工程,2013,21(6):1576-1585.

[11] Rodriguez P,Wohlberg B.Efficient minimization method for a generalized total variation functional[J].IEEE Transactions on Image Processing,2009,18(2):322-332.

[12] Bube K,Langan R.Hybrid l1/l2minimization with applications to tomography[J].Geophysics,1997,62(4):1183-1195.

[13] 张同兵,谢建,朱建军.预处理共轭梯度法解病态问题及在GPS中的应用[J].测绘工程,2010,19(4):60-63.

收稿日期：2015-01-12。陕西省自然科学基金项目(2013JM80 25)。周芹，硕士生，主研领域：图像超分辨率重建。马志强，副教授。单勇，讲师。

中图分类号TP391

文献标识码A

DOI:10.3969/j.issn.1000-386x.2016.07.051

SUPER RESOLUTION RECONSTRUCTION WITH GENERALISED TOTAL VARIATION BASED ON ITERATIVELY REWEIGHTING

Zhou QinMa ZhiqiangShan Yong

(SchoolofInformationandNavigation,AirForceEngineeringUniversity,Xi’an710077,Shaanxi,China)

AbstractSince conventional superresolution reconstruction algorithm cannot restrain image noise effectively under the condition of serious blur and noise, we proposed the superresolution reconstruction algorithm with generalised total variation which is based on iteratively reweighting norm. The algorithm uses the iteratively weighted data fidelity term and the regularisation term to construct the cost function of generalised total variation, and adopts the preconditioned conjugate gradient method to optimise the solution, so that it can effectively suppress noise generation. Experiment proved that the algorithm could well preserve the image details while removing noise, and had good visual effect.

KeywordsImage superresolutionGeneralised total variationIteratively reweightingPreconditioned conjugate gradientDenoising