一种基于SIFT特征的快速图像匹配算法

杨　松　邵龙潭　宋维波　刘　威

1(大连理工大学工业装备结构分析国家重点实验室　辽宁 大连 116024)2(大连海洋大学信息工程学院　辽宁 大连 116023)



一种基于SIFT特征的快速图像匹配算法

杨松1,2邵龙潭1宋维波2刘威2

1(大连理工大学工业装备结构分析国家重点实验室辽宁 大连 116024)2(大连海洋大学信息工程学院辽宁 大连 116023)

摘要经典的SIFT算法具有良好的尺度、旋转、光强不变特性而广泛应用于图像匹配。图像特征点较少时，匹配过程使用穷举法查找最近邻匹配点；当图像特征点较多时采用KD-Tree结构，而其检索过程存在“回溯”现象，这两种方法的匹配效率都不高。为了提高特征点的匹配速度，提出改进的SP-Tree结构解决“回溯”问题。在结点集分割时设置参数合理确定左右超平面位置，引入平衡因子作为结点分割方法选择的依据，采用近似最近邻搜索算法加快特征点匹配速度。给出算法的详细实现过程，并应用两幅图像进行验证。实验结果表明：SIFT特征向量采用改进SP-Tree结构在损失少部分匹配点的同时，提高了SIFT特征点的整体匹配速度，适合于图像特征的实时匹配过程。

关键词图像匹配SIFT特征KD-TreeSP-Tree最近邻搜索

0引言

图像匹配是一种研究同一场景中两个不同视角下的图像之间对应关系的技术，是计算机视觉应用研究的起点和基石，已广泛应用于图像的拼接与融合、目标的识别与跟踪、摄像机标定、图像检索以及三维重构等领域[1-4]。目前，图像匹配[5]方法主要有基于面积、比值和相位等算法，它们存在着共同的缺点：图像拍摄的焦距要相同，且图像旋转角度和变形不能太大，这极大地限制了它们的广泛应用。近年来，基于图像局部不变性特征的图像匹配算法以其计算简单、精度高和鲁棒性好等特点成为目前研究的热点。哥伦比亚大学的Lowe在1999年提出并逐步完善的SIFT算法[6,7]。该算法是通过构建金字塔和利用高斯核滤波差分来实现的，该算法不仅具有图像旋转、尺度变换、仿射变换和视角变化条件下的不变性特征，对目标的运动、遮挡、噪声等因素影响也能达到较好的匹配效果。Mikolajczyk提出了基于Harris-Laplace和Hessian-Laplace特征匹配算法[8]，该算法具有仿射不变性，但检测到的特征点数较少。Bay在2006年提出SURF(Speed-up Robust Feature)算法[9]，进一步提高了特征的提取速度，但在尺度和旋转的适应性方面不及SIFT算法。优秀的图像匹配算法不仅要求图像特征点具有稳定的表征形式，而且还需要有快速的特征点配准算法。SIFT算子通过计算特征向量间的欧式距离来衡量其相似度。其特征向量的维数为128维，相似度计算的速度会较慢，而且特征点配对过程采用全局搜索法，其搜索过程的效率不高，尤其特征点数目较多时，整个图像匹配过程将非常耗时。为此，学者们从两个方面研究和改进SIFT算子：一个研究方面是降低特征向量的维数[10，11]，如PCA、SPCA算法，运用主成分分析法提取特征向量的主成分，压缩向量数据，降低特征向量的维数，从而减少特征点相关性计算时间，但会导致匹配准确率的降低。此外，一些算法[12-14]引入其他一些特征点的表征形式，可以在降低特征向量维数的同时保持较好的匹配准确率。研究的另一方面是采用特殊的结构[15]，如KD-Tree[16]、改进KD-Tree[17]等。通过构建特征点存储的二叉树，同时结合最近邻搜索算法，加快特征向量的匹配搜索速度，从而缩短图像特征点的匹配时间。

在对Metric-Tree结构进行研究的基础上，采用SP-Tree[18]结构存储图像特征点。SP-Tree是一种高效查询的二叉树，其检索过程不会产生“回溯”问题。SP-Tree的建树过程通过设置参数合理确定左右超平面位置，引入平衡因子作为结点分割方法选择的依据，采用近似最近邻搜索算法加快特征点的匹配过程。文中给出SP-Tree结点的结构定义、二叉树建树的过程和最近邻结点搜索算法的具体实现过程，并将其应用在图像特征点的实时匹配过程中，取得较好的效果。

1SIFT特征描述

SIFT图像匹配算法的特征描述子提取过程[17]包括：首先利用变尺度高斯核函数与图像通过卷积运算建立图像的高斯差分多尺度空间，将同一尺度下的8个相邻点和上下相邻尺度对应的18个点共26个点进行比较，找出图像的局部极值点作为候选关键点；然后通过二次函数计算特征点的精确位置，再通过计算该位置的高斯差分响应值及曲率去除对比度低的极值点和不稳定的边缘响应点，确定特征点的主方向，使算子获得更好的旋转不变性。以特征点为中心取16×16个像素的邻域范围(图1以8×8为例)，进而分成16个4×4的子块，提取8个方向(45°间隔)上的梯度值，构成128维的SIFT算子的特征向量，对其进行向量归一化后并对梯度幅值进行限制，以去除光照变化的影响。

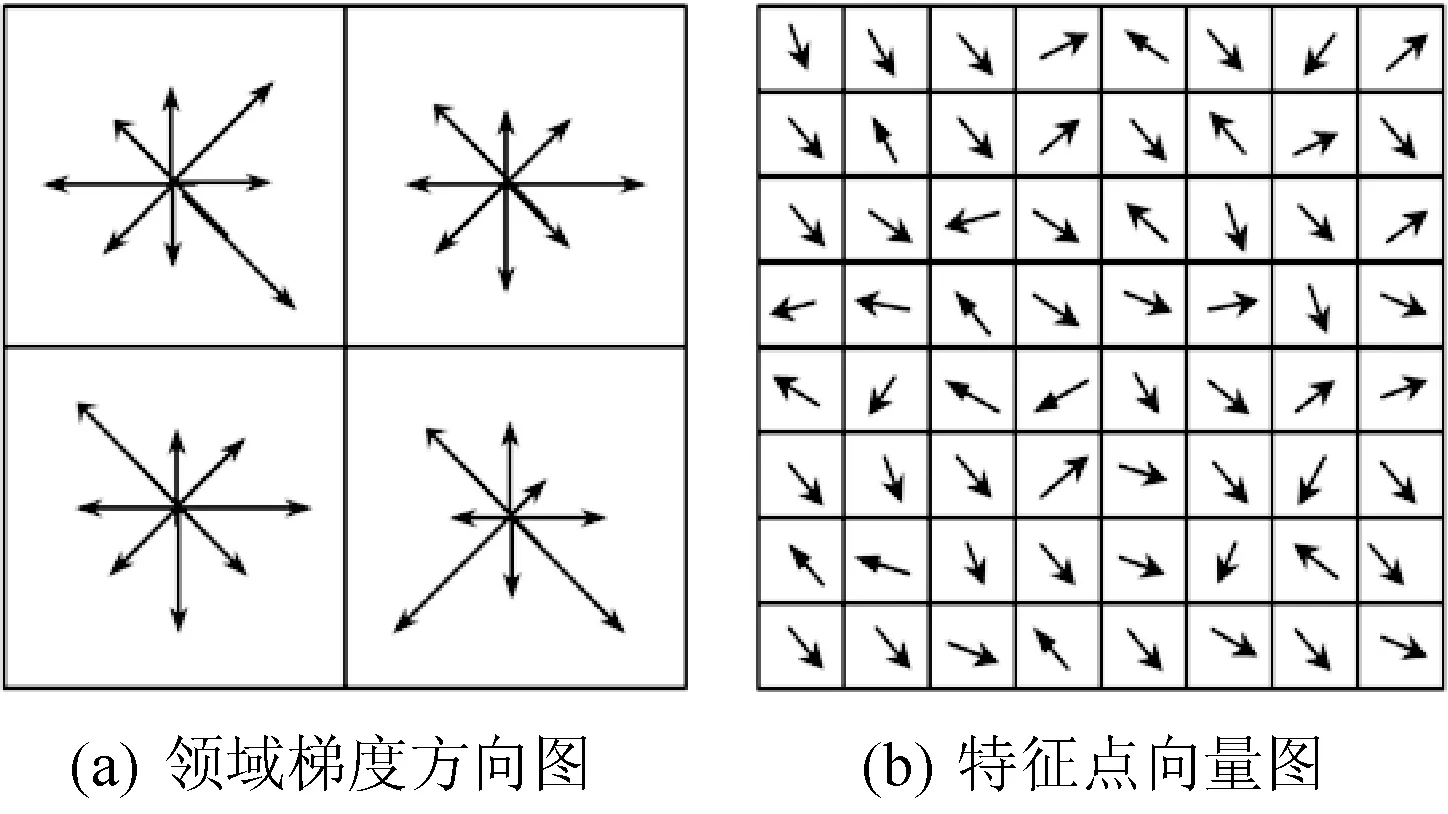
图1　SIFT特征点示意图

2特征向量匹配算法

通过上述过程生成图像的特征点描述子，包含每个特征点的位置、尺度和方向等信息。在理想状态下的两幅图像相同部分的特征点应具有相同的特征描述子，它们之间的距离应该最近，因而可以采用最近邻搜索方法寻找图像特征点的对应关系。衡量特征点相似程度的度量有欧式距离[17]、斜面距离[19]等。

近年来，KD-Tree结构被用于特征向量的匹配过程，可以加快搜索速度，其搜索过程包括两部分时间开销：一部分是一个特征点集合的建树时间，这部分是固定的，且较为耗时，这也是当特征点规模较小时不采用KD-Tree搜索的原因。另一部分是在建好的KD-Tree中进行最近邻搜索时间。在KD-Tree中进行最近邻搜索时容易产生“回溯”搜索过程，KD-Tree在第S维度上的空间划分的示意图如图2(a)所示，在分割超平面两边分布有数目相当的数据点。当查询点位于分割超平面附近时，因为其最近邻有可能落在分割超面的另一边，其“回溯”操作必须进行。针对这个问题，近年来研究人员提出了不少改进方案，如回溯搜索从优先级最高的树结点开始，确保优先搜索包含最近邻点可能性较高的空间[17]等。本文针对KD-Tree的“回溯”问题，提出改进SP-Tree算法，缩短了最近邻特征向量的搜索时间。

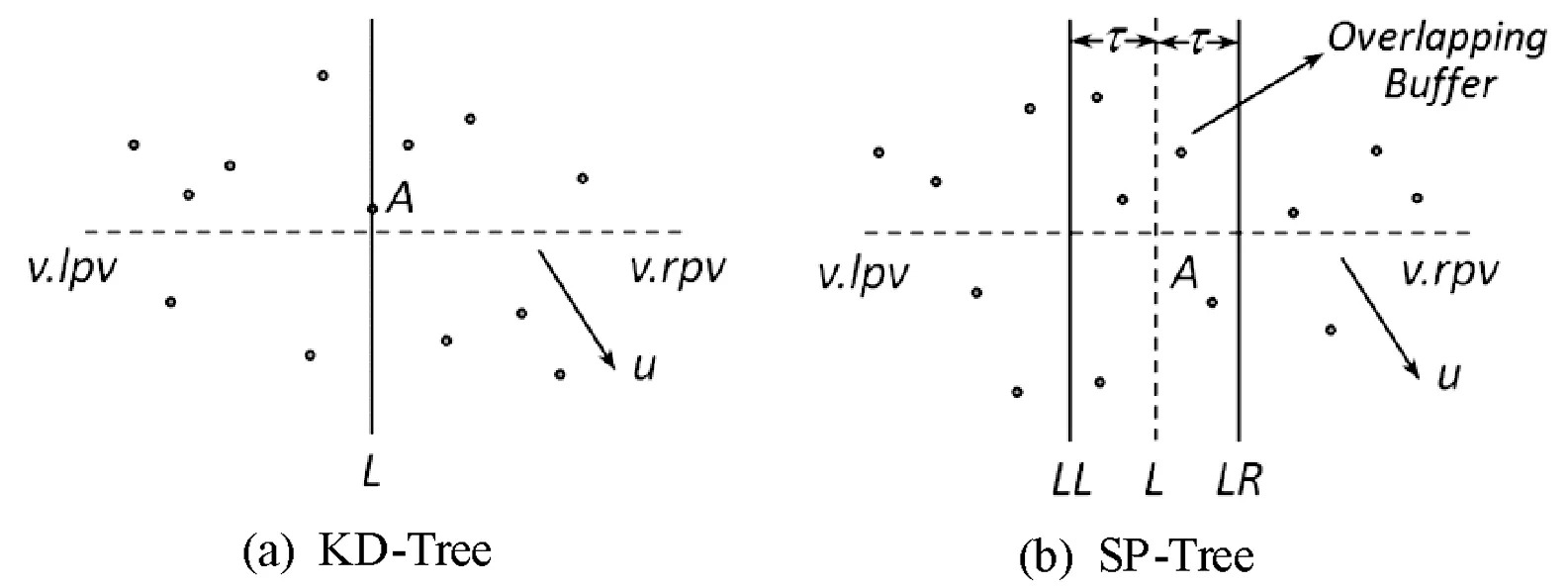
图2　KD-Tree和SP-Tree空间划分示意图

3最近邻搜索算法

3.1Metric-Tree[20]

Metric-Tree是一棵二叉树，它的结点都是点的集合，根结点代表了所有点的集合。对于非叶子结点v所代表的集合N(v)被分割成两个子集，分别用v的两个孩子结点v.lc和v.rc表示，满足式(1)和式(2):

N(v)=N(v.lc)∪N(v.rc)

(1)

∅=N(v.lc)∩N(v.rc)

(2)

3.2结点分割算法

建立Metric-Tree的关键是如何分割结点v，方法如下：

步骤1从N(v)中选择两个枢纽点v.lpv和v.rpv，满足:

‖v.lpv-v.rpv‖=maxp1,p2∈N(v)‖p1-p2‖

(3)

步骤3每个结点包含一个中心点为v.center，半径为v.r的超球B，满足N(v)∈B(v.center,v.r)。

4SP-Tree结构

4.1SP-Tree定义

如图1(b)所示，SP-Tree在Metric-Tree的基础上改进的，在超平面L左右两侧以距离τ为间距分别作平行于超平面L的超平面LL和LR。

N(v)中LL右侧的点划分到v.rc中，LR左侧的点划分到v.lc中，即：

N(v.lc)={x|x∈N(v),d(x,LR)+2τ>d(x,LL)}

(4)

N(v.rc)={x|x∈N(v),d(x,LL)+2τ>d(x,LR)}

(5)

4.2改进的SP-Tree搜索

在SP-Tree的基础上，做出改进如下：在结点分割算法中需要确定左右超平面，可以在超平面左右距离为τ建立左右超平面。但是在进行结点超平面确定时为了保证左右孩子结点中包含的特征点数相等，而使得超平面并非过中心点，超平面左右并不对称，超平面法向量在超平面左右的长度分别为ll和lr，且ll！=lr，这里引入参数α(0<α<1)，设置左右超平面距离分别为ll×α和lr×α，这种设置方法更为合理。

不是所有的结点都要进行重叠划分，定义一个平衡因子ρ(一般取0.7)，如果对于取定的τ(已被上式替换)，划分后结点v的任一孩子结点包含的点数大于ρ‖N(v)‖时，则按Metric-Tree的分割方式对结点v重新进行划分；否则，保留原先的划分方式，继续对其孩子结点按上述方法进行分割，直到结点包含的点数达到叶子结点的要求为止，近似最近邻查询与SP-Tree相同。

4.3近似的最近邻搜索

对于查询q，如果当前结点为v，q在v结点超平面L的左侧，则递归地查询v的左孩子v.lc；否则递归地查询v的右孩子v.rc，直到查询到叶子结点，则认定该叶子结点为q的最近邻结点。

4.4具体的算法实现

给出算法的具体定义和实现过程，采用Matlab语言表示：

(1)SP-Tree的二叉搜索树结构和超平面的定义

structSpTreeNode

{

set N;

//该结点包含的特征点集合

SpTreeNode *lc;

//左孩子指针

SpTreeNode *rc;

//右孩子指针

HyperplanehPlane;

//超平面

HyperplanelhPlane;

//左超平面

HyperplanerhPlane;

//右超平面

Point center;

//特征向量组成的超球的中心点，初始值为空间原点

int radius;

//该特征点集空间的超球半径，初始值为0

bool overlapping;

//是否重叠划分标志，初始值为false

boolisleaf;

//是否为叶子结点标志，初始值为false

};

structHyperplane

{Point PointOnPlane;

//超平面上一点，默认值为空间原点

NormalVectornVector;

//超平面法向量，默认值为零向量

};

//用超平面上一点和其法向量表示该超平面

(2) SP-Tree的建立算法

步骤1初始化一个SpTreeNode队列；

步骤2创建根结点RootNode，入队；

步骤3若队列非空，取出队首元素SpCurNode，判断该结点包含的特征点集合大小；若大于叶子结点允许包含的最大特征点数，则按照分割算法来分割该结点为两个结点lcNode和rcNode，SpCurNode.lc = &lcNode，SpCurNode.rc = &rcNode，并将lcNode和rcNode入队；否则，修改结点的isleaf标志，队首元素直接出队；若队列为空，则退出算法；

步骤4转向步骤3执行。

(3) SP-Tree的根结点建立算法

步骤1初始化一个SpTreeNode型变量RootNode；

步骤2将所有特征点的索引值加入RootNode.N中(为了节省空间，对所有特征点集合只保留一个全局副本，树结点中的成员变量N只保存该结点中特征点在副本中的索引值)；

步骤3计算RootNode.center(为了减小时间复杂度，取所有特征向量对应维度上最大最小值的平均值作为中心点在该维度上的值)；

步骤4计算超球半径RootNode.radius(超球空间中所有特征向量距中心点的距离最大值)；

步骤5确定超平面RootNode.hPlane；

步骤6左右超平面RootNode.lhPlane；RootNode.rhPlane初始化为默认值，RootNode.overlapping初始化为false，左右孩子指针初始化为NULL。

(4) 确定超平面RootNode.hPlane算法

步骤1在RootNode.N找到距离最远的两个特征向量lpv和rpv，采用近似算法：先找到距离中心点最远的特征点lpv，再以lpv为基准找到距离lpv最远的点rpv，RootNode.hPlane.nVector=rpv-lpv;

步骤2对所有属于RootNode.N的特征向量v，统计v-lpv在RootNode.hPlane.nVector上的投影值，找出所有投影值的中位数median，则RootNode.hPlane.PointOnPlane = lpv+median/dist(RootNode.hPlane.nVector)*RootNode.hPlane.nVector。

(5) 结点分割算法

不是所有的结点都要进行重叠划分，定义一个平衡因子(一般取0.7)，如果对于取定的、重叠划分后结点的任一孩子结点包含的点数大于*SpCurNode.N.size()时，则按Metric-Tree的分割方式对结点进行划分；否则进行重叠划分，具体步骤如下：

步骤1初始化两个SpTreeNode：lcNode、rcNode；

步骤2在当前结点超平面SpCurNode.hPlane左右两侧作超平面的平行平面lhPlane、rhPlane，超平面法向量在超平面左右的长度分别为ll和lr，分别在距离ll×ratio和lr×ratio (0

步骤3分别作如下操作：

① 用两个集合lcN、rcN记录分割后左右孩子中包含的特征点索引；

② 首先用lcN、rlN分别记录rhPlane和lhPlane的右侧和左侧的特征点，并计算点数rhpCount、lhpCount；可以通过特征点与超平面上的点组成的向量在超平面上法向量上的投影的正负来判断在超平面的哪一侧；

③ 判断(lhpCount>pho*SpCurNode.N.size()|| rhpCount>pho*SpCurNode.N.size())，若为假，则：

SpCurNode.lhPlane = lhPlane，SpCurNode.rhPlane=rhPlane，SpCurNode.overlapping = true；

若为真，则SpCurNode.overlapping = false，修改lcN、rlN分别记录lPlane左右两侧的特征点；

④ lcNode.N = lcN，rcNode.N = rcN，再分别计算lcNode.center、rcNode.center、lcNode.radius、rcNode.radius、lcNode.hPlane、rcNode.hPlane，其他成员仍为默认值，返回。

(6) 最近邻查询

给定一个特征向量，先查询根结点，若在根结点超平面的左侧则递归地查询左孩子结点；否则，递归地查询右孩子结点，直到当前结点为叶子结点。顺序查询叶子结点中包含的特征向量，找到最近点和次近点后返回。

5实验结果与分析

本文提取图像SIFT特征进行点匹配实验，所有编程都在Matlab 7.0环境下，实验用计算机的配置如下：CPU：Intel Core i3-370，主频2.4 GHz，内存2 GB，操作系统为Windows 7。实验采用标准图像Lena、Building进行测试，搜索到最近邻特征点后，采用比值提纯法[17]剔除实际未匹配的特征点。如图3-图6所示。

图3　Lena图像

图4　三种匹配算法的比较

图5　Building图像

图6　三种匹配算法的比较

通过表1的对比可知，采用改进SP-Tree结构进行特征点匹配具有很快的速度。若图像特征点较少，则采用穷举算法则取得较好的效果，因为KD-Tree结构建树还需要花费较多时间。当图像特征点较多时(超过2500个[17])，选用KD-Tree+BBF效果较好。本文的SP-Tree算法执行时间包括建SP -Tree的过程和在二叉树中进行近似最近邻搜索的过程，在损失少部分匹配特征点的情况下，匹配速度有较大的提升，适合对图像特征点匹配要求不高的情况。

表1　三种匹配方法实验结果对比(匹配时间:s)

6结语

本文给出SP-Tree结构的定义，并对特征点建树、最近邻匹配点搜索过程进行详细说明，消除KD-Tree树搜索过程的“回溯”问题。通过对标准图像进行SIFT特征匹配实验，并与原有的匹配算法和BBF-KD-Tree匹配算法进行比较得出，本文算法在减少部分匹配点对的同时，其匹配速度有显著的提升，可应用于特征点实时匹配过程。

参考文献

[1] Brown M,Lowe D G.Recognizing panoramas[C]//Proceeding of the 9thInternational Conference on Computer Vision(ICCV03),Nice,France:IEEE,2003:1218-1225.

[2] 杨云涛,冯莹,曹毓,等.基于SURF的序列图像快速拼接方法[J].计算机技术与发展,2011,21(3):6-9,14.

[3] Jegou H,Harzallah H,Schmid C.A contextual dissimilarity measure for accurate and efficient image search[C]//Proceeding of the Conference on Computer Vision & Pattern Recognition.Minneapolis,USA,2007:1-8.

[4] 王剑,周国民.图像三维重建中的特征点匹配方法研究[J].计算机工程与应用,2009,45(2):10-12.

[5] Zitova B,Flusser J.Image registration methods:a survey[J].Image and Vision Computing,2003,21(11):977-1000.

[6] Lowe D G.Object recognition from local scale invariant features[C]//Corfu,Greece. International Conference on Computer Vision,1999:1150-1157.

[7] Lowe D G.Distinctive image features from scale-invariant key-points[J].International Journal of Computer Vision,2004,60(2):91-110.

[8] Mikolajczyk K,Schmid C.Indexing based on scale invariant interest points[C]//The Proceeding of the 8thInternational Conference on Computer Vision(ICCV01),Vancouver,2001:525-531.

[9] Bay H,Tuytelaars T,VanGool L.Surf:Speeded up robust features[C]//The 9thEuropean Conference on Computer Vision(ECCV06),GRAZ,2006:404-417.

[10] Ke Y,Sukthankar R.PCA-SIFT:A more distinctive representation for local image descriptors[C]//Proceedings of IEEEComputer Society Conference on Computer Vision and Pattern Recognition,Washington,D.C.,2004:506-513.

[11] 吴贤伟,岑杰,邰晓英.一种快速图像特征降维方法:SPCA[J].宁波大学学报:理工版,2005,18(3):336-339.

[12] 刘立,彭复员,赵坤,等.采用简化SIFT算法实现快速图像匹配[J].红外与激光工程,2008,37(1):181-184.

[13] 郑永斌,黄新生,丰松江.SIFT和旋转不变LBP相结合的图像匹配算法[J].计算机辅助设计与图形学学报,2010,22(2):286-291.

[14] 石钊铭,耿伯英,董银文.基于改进SIFT的航拍图像快速匹配方法[J].指挥控制与仿真,2013,35(1):106-110.

[15] Bentley J L.Multidimensional binary search trees used for associative searching[J].Communications of the ACM,1975,18(9):509-517.

[16] 杜振鹏,李德华.基于KD-Tree搜索和SURF特征的图像匹配算法研究[J].计算机与数字工程,2012,40(2):96-98,126.

[17] 王永明,王贵锦.图像局部不变性特征与描述[M].北京:国防工业出版社,2010.

[18] Liu T,Moore A W,Gray A,et al.An investigation of practical approximate nearest neighbor algorithms[M].NIPS,MIT Press,Cambridge,2005.

[19] 傅卫平,秦川,刘佳,等.基于SIFT算法的图形目标匹配与定位[J].仪器仪表学报,2011,32(1):163-169.

[20] Ciaccia P,Patella M,Zezula P.M-Tree:An efficient access method for similarity search in metric spaces[C]//Proceedings of 23rdVLDB International Conference,Athens,Greece,1997:426-435.

收稿日期：2015-03-04。国家自然科学基金项目(50905022，5130 9047)；国家高技术研究发展计划项目(2010CB7315022)；工业装备结构分析国家重点实验室专项基金项目(S09104)。杨松，副教授，主研领域：数字图像处理，模式识别。邵龙潭，教授。宋维波，讲师。刘威，讲师。

中图分类号TP391

文献标识码A

DOI:10.3969/j.issn.1000-386x.2016.07.043

A QUICK IMAGE MATCHING ALGORITHM BASED ON SIFT FEATURE

Yang Song1,2Shao Longtan1Song Weibo2Liu Wei2

1(StateKeyLaboratoryofStructuralAnalysisofIndustrialEquipment,DalianUniversityofTechnology,Dalian116024,Liaoning,China)2(InstituteofInformationEngineering,DalianOceanUniversity,Dalian116023,Liaoning,China)

AbstractDue to its good invariant characteristics in scaling, rotation and light intensity, the classic SIFT algorithm has been widely used in image matching. If there are fewer image feature points, the exhaustion method is used to find the nearest matching point. If there are more image feature points, KD-tree will then be used, but the backtracking phenomenon exists in its retrieval process, so the matching efficiency of both methods are low. In order to improve feature points matching speed, we propose an improved SP-Tree structure to solve the backtracking problem. The parameter α is set to determine a reasonable location about hyper-plane in node set segmentation, and a balancing factors ρ is introduced as the choice basis for different node segmentation method, and the approximate nearest searching algorithm is adopted, which can accelerate the speed of feature points matching. In the paper we give the detailed implementation process of the algorithm and the validations with two standard images. Experimental results show that the SIFT feature vector, by using a modified SP-Tree structure, at the expense of few matching points, greatly improves the overall speed of SIFT feature points matching. It is suitable for image features matching in real time.

KeywordsImage matchingSIFT featureKD-TreeSP-TreeNearest neighbour search