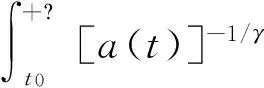二阶非线性变时滞中立型微分方程的振荡性分析

于　强，杨甲山

(1. 辽东学院 师范学院数学系，辽宁 丹东118003； 2. 梧州学院 信息与电子工程学院，广西 梧州 543002)



二阶非线性变时滞中立型微分方程的振荡性分析

于强1，杨甲山2

(1. 辽东学院 师范学院数学系，辽宁 丹东118003； 2. 梧州学院 信息与电子工程学院，广西 梧州 543002)

摘要:研究一类具有变时滞的二阶中立型泛函微分方程的振荡性.利用Riccati变换技术及一些分析技巧，获得该类方程振荡的两个新的判别准则和两个比较性判别定理，这些结论推广且改进了现有文献中的一些结果.所举的两个例子说明所得定理的假设条件是较宽松的.

关键词:振荡性；变时滞；泛函微分方程；Riccati变换

微分方程在自然科学和工程技术等领域均有非常广泛的应用，如二阶Emden-Fowler型微分方程x′′(t)+at-1x′(t)+btm-1xn(t)=0广泛应用于数学物理、理论物理(特别是核物理)及化学物理等领域，因此，近来变时滞的中立型泛函方程振荡性的研究引起了国内外学者的广泛兴趣[1-21].笔者考虑如下形式的二阶非线性中立型变时滞微分方程

(1)

的振荡性，(1)式中，a,p,q∈C([t0,+),R)；γ为两个正奇数之商；f∈C(R,R)且uf(u)>0(u≠0).并总假设以下条件成立

(H1) a∈C1([t0,+),(0,+))，q(t)>0，p(t)≥0.

(H2) 滞量函数τ,δ:[t0,+)→(0,+),满足τ(t)≤t且，为常数).

(H3) 存在常数L>0，使得当u≠0时，f(u)/u≥L.

称函数x(t)∈C1([Tx,+),R)(Tx≥t0)是方程(1)的一个解，如果函数x(t)满足a(t)[(x(t)+p(t)x(τ(t)))′]γ∈C1([Tx,+),R)，且在区间[Tx,+)满足方程(1).这里只讨论方程(1)的非平凡解.如果方程(1)的一个解x(t)既不最终为正也不最终为负，则称它为是振荡的，否则称它是非振荡的；如果方程(1)的所有解都是振荡的，则称它为是振荡的.作者将考虑方程(1)分别在条件

(2)

和

(3)

成立的情况下的振荡性判别准则.

1主要结果及其证明

为了方便，记

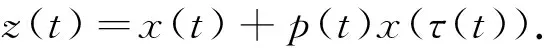
(4)

引理1设A>0，B>0和λ>0均为常数，则当x>0时，有

当x<0时，有

定理1设条件(2)成立且0≤p(t)≤p0<+(p0为常数)，如果存在函数φ∈C1([t0,+),(0,+)),使得

(5)

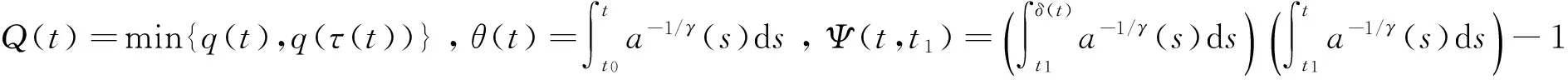
证明反证法，设方程(1)存在一个非振荡解x(t)，不妨设x(t)为最终正解(当x(t)为最终负解时类似可证)，则Q(t)，使得当t≥t1时，有x(t)>0，z(t)≤x(t)+p0x(τ(t))，x(δ(t))>0，于是由z(t)的定义知，τ·δ=δ·τ且z(t)≥x(t)(t≥t1).由方程(1)，得

(6)

由(6)式容易推得z′(t)>0(t≥t1).应用(6)式，当t≥t1时，有

(7)

于是，综合(6)式及(7)式，当t≥t1时，可得

注意到τ′(t)≥τ0>0，τ°δ=δ°τ及z(t)≤x(t)+p0x(τ(t))和Q(t)的定义，上式进一步可写成

(8)

作Riccati变换,有

(9)

则w(t)>0(t≥t1)，注意到(9)式及τ′(t)≥τ0>0，有

由于a(t)[z′(t)]γ是单调减少的，所以

即

注意到引理1，有

(10)

再作Riccati变换，有

(11)

则v(t)>0(t≥t1)，类似地，可推得

(12)

于是，由(10)式和(12)式，并注意到(8)式及z′(t)>0，有

(13)

由于a(t)[z′(t)]γ(t≥t1)是单调减少的，有

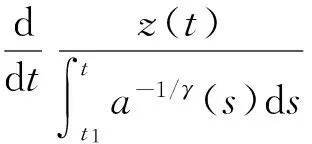
(14)

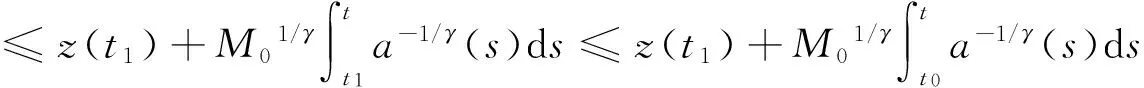
(15)

将(14),(15)式代入(13)式，得

于是

这与(5)式矛盾.定理证毕.

注1当γ=1时,定理1即为文[14]中的定理2.1，但这里去掉了文[14]中的限制条件“δ′(t)>0且δ(t)≤τ(t)”.

定理2设条件(3)成立且0≤p(t)≤p0<+(p0为常数)，如果存在函数φ∈C1([t0,+),(0,+))，使得(5)式成立，且

(16)

其中:常数T≥t0足够大，函数

证明反证法，设方程(1)存在一个非振荡解x(t)，不妨设x(t)为最终正解，则∃t1≥t0，使得当t≥t1时，有x(t)>0，x(τ(t))>0，x(δ(t))>0，由定理1的证明知a(t)[z′(t)]γ是严格单调减少的且最终定号，从而z′(t)最终为正或最终为负.所以，只需考虑下列两种情形：(a) 当t≥t1时,z′(t)>0； (b) 当t≥t1时,z′(t)<0.

情形(a)当t≥t1时,z′(t)>0.此时同定理1的证明，知方程(1)是振荡的.

情形(b)当t≥t1时,z′(t)<0.定义函数w(t)为

(17)

则w(t)<0,t≥t1，且

(18)

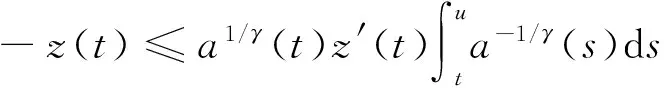
(19)

再定义函数v(t)为

(20)

则v(t)<0(t≥t1).类似地，同样可得

(21)

(22)

于是，综合(18),(21)式并应用(8)式(由定理1的证明知，(8)式仍然成立)及z(δ(t))≥z(t)，得

(23)

当γ>1时，由z(t)>0，z′(t)<0(t≥t1)，知z(t)≤z(t1)，即z1-γ(t)≥z1-γ(t1)=k.当γ=1时，z1-γ(t)=1.当γ<1时，再次利用a(t)[z′(t)]γ的单调减少性，得当s≥t≥t1时，有a(s)[z′(s)]γ≤a(t)[z′(t)]γ，即z′(s)≤{a(t)[z′(t)]γ}1/γa-1/γ(s)，进一步就有

即

其中:M=-{a(t1)[z′(t1)]γ}1/γ=-a1/γ(t1)z′(t1)>0为常数，在上式中令u→+，得

即

综合上述3种情形及函数η的定义，根据(23)式，有

两边同乘以ζγ(t)并从t1到t(t≥t1)积分，由分部积分法，并分别注意到ζ′(t)=-a-1/γ(t)及(19)和(22)式，以及引理1，可得

因此

这与(16)式矛盾.定理证毕.

下面给出方程(1)振荡的两个比较性定理.

定理3设条件(2)成立且0≤p(t)≤p0<+(p0为常数)，若存在函数η∈C1([t0,+),(0,+)),使得η(t)≤δ(t)且，如果一阶微分不等式

(24)

没有正解，其中t1≥t0足够大，函数θ(t)的定义如定理1，则方程(1)是振荡的.

证明反证法，设方程(1)存在一个非振荡解x(t)，不妨设x(t)为最终正解，则∃t1≥t0，使得当t≥t1时，有x(t)>0，x(τ(t))>0，x(δ(t))>0.由定理1的证明知，当t≥t1时,z(t)>0，z′(t)>0，[a(t)(z′(t))γ]′<0且(8)式成立.于是由(8)式得

(25)

由于当t≥s≥t1时，有a(t)(z′(t))γ≤a(s)(z′(s))γ，即a1/γ(s)z′(s)≥a1/γ(t)z′(t)，所以

利用η(t)≤δ(t)，由(25)式，得

令y(t)=a(t)(z′(t))γ，则y(t)是(24)的一个正解，矛盾.定理证毕.

定理4设条件(3)成立且0≤p(t)≤p0<+(p0为常数)，若存在函数η,ξ∈C1([t0,+),(0,+)),使得η(t)≤δ(t)≤ξ(t)且(t)=+，如果一阶微分不等式(24)和

(26)

没有正解，其中t1≥t0足够大，函数ζ(t)的定义如定理2，则方程(1)是振荡的.

证明反证法，设方程(1)存在一个非振荡解x(t)，不妨设x(t)为最终正解，则∃t1≥t0，使得当t≥t1时，有x(t)>0，x(τ(t))>0，x(δ(t))>0.由定理1的证明知(8)式成立，进一步，(25)式仍成立.同定理2，只需考虑下列两种情形：(a) 当t≥t1时,z′(t)>0，[a(t)(z′(t))γ]′<0； (b) 当t≥t1时,z′(t)<0，[a(t)(z′(t))γ]′<0.

情形(a)当t≥t1时,z′(t)>0，[a(t)(z′(t))γ]′<0.此时，同定理3的证明，方程(1)是振荡的.

(27)

于是结合条件δ(t)≤ξ(t)和(27)式，并记y(t)=a(t)(z′(t))γ，由(25)式得

亦即

这就是说v(t)=-y(t)>0是(26)的一个正解，矛盾.定理证毕.

注2当γ=1，f(u)=u时，定理4的结论即为文献[12]中的定理1.

例1对常数α>0，考虑二阶时滞微分方程

(E1)

其中：γ=1，a(t)≡1，p(t)=2/3，q(t)=α/t2，τ(t)=t-1，δ(t)=t，f(u)=u.显然，条件(H1)～(H3)均满足.若取φ(t)=t，由定理1(注意到此时L=1，p0=2/3，τ0=1且Ψ(s,t1)=1)，则

所以由定理1知，当α>5/12≈0.416 67时方程(E1)是振荡的.

注3现用文[13]的定理2.1来判定.由于

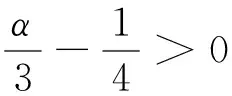
例2考虑二阶泛函微分方程

(E2)

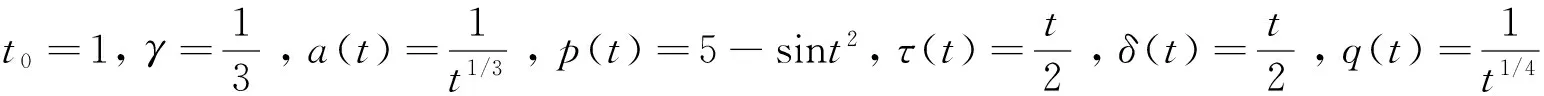
取f(u)=u[1+ln(1+u4)]，由于0

显然条件(H1)～(H3)全部满足.由于

为了计算简单，在定理1中取φ(t)=1，T=5，则

所以定理1的条件均满足，故由定理1知，方程(E2)是振荡的.

注4由于方程(E2)的中立项系数函数p(t)>1，因此文献[1-3,6-9,13-18,20-21]等中的定理都不能用于方程(E2).

参考文献：

[1]HASANBULLI M, ROGOVCHENKO Y V. Oscillation criteria for second order nonlinear neutral differential equations[J]. Applied Mathematics and Computation, 2010, 215 (12): 4392-4399.

[2]LI T X, AGARWAL R P, BOHNER M.Some oscillation results for second-order neutral differential equations[J]. The Journal of the Indian Mathematical Society, 2012, 79 (1/2): 97-106.

[3]LI T X, AGARWAL R P, BOHNER M.Some oscillation results for second-order neutral dynamic equations[J]. Hacettepe Journal of Mathematics and Statistics, 2012, 41 (5): 715-721.

[4]LI T X, YU V. Oscillatory behavior of second-order nonlinear neutral differential equations[J]. Abstract and Applied Analysis, 2014, 14 (1): 1-5.

[5]LI T X, ROGOVCHENKO Y V, ZHANG C H. Oscillation of second-order neutral differential equations[J]. Funkcialaj Ekvacioj, 2013, 56 (1): 111-120.

[6]SUN S R, LI T X, HAN Z L, et al. Oscillation theorems for second-order quasilinear neutral functional differential equations[J]. Abstract and Applied Analysis, 2012, 26 (3): 1-17.

[7]Zhang C, Agarwal R P, Bohner M, et al. New oscillation results for second-order neutral delay dynamic equations[J]. Advances in Difference Equations, 2012， 227： 15-19.

[8]ZHONG J, OUYANG Z, ZOU S. An oscillation theorem for a class of second-order forced neutral delay differential equations with mixed nonlinearities[J]. Applied Mathematics Letters, 2011, 24 (8): 1449-1454.

[9]AGARWAL R P, BOHNER M, LI T X, et al.A new approach in the study of oscillatory behavior of even-order neutral delay differential equations[J]. Appl Math Comput, 2013, 225: 787-794.

[10]YANG J S, QIN X W. Oscillation criteria for certain second-order Emden-Fowler delay functional dynamic equations with damping on time scales[J]. Advances in Difference Equations, 2015， 97： 33-39.

[11]YANG J S, QIN X W, ZHANG X J.Oscillation criteria for certain second-order nonlinear neutral delay dynamic equations with damping on time scales[J]. Mathematica Applicata, 2015, 28 (2): 439-448.

[12]LI T X, ROGOVCHENKO Y V, ZHANG C H. Oscillation of second-order neutral differential equations[J]. Funkcialaj Ekvacioj, 2013, 56: 111-120.

[13]YE L, XU Z. Oscillation criteria for second order quasilinear neutral delay differential equations[J]. Applied Mathematics and Computation, 2009, 207 (2): 388-396.

[14]SUN S R, LI T X, HAN Z L, et al. On oscillation of second-order nonlinear neutral functional differential equations[J]. Bull Malays Math Sci Soc, 2013, 36 (3): 541-554.

[15]杨甲山, 方彬. 一类二阶中立型微分方程的振动性[J]. 数学的实践与认识, 2013, 43 (23): 193-197.

[16]杨甲山, 覃学文. 具阻尼项的高阶Emden-Fowler型泛函微分方程的振荡性[J]. 中山大学学报 (自然科学版), 2015, 54 (4): 63-68.

[17]杨甲山. 具正负系数和阻尼项的高阶泛函微分方程的振动性[J]. 华东师范大学学报 (自然科学版), 2014 (6): 25-34.

[18]杨甲山, 莫协强. 时间模上一类二阶非线性动态方程的振动结果[J]. 安徽大学学报 (自然科学版), 2015, 39 (1): 1-7.

[19]杨甲山. 时标上一类具阻尼项的二阶动态方程的振荡性[J]. 系统科学与数学, 2014, 34 (6): 734-751.

[20]AGARWAL R P, BOHNER M, LI T X, et al. Oscillation of second-order Emden-Fowler neutral delay differential equations[J]. Annali di Matematica Pura ed Applicata, 2014, 193 (6): 1861-1875.

[21]ZHANG C H, SENEL M T, LI T X. Oscillation of second-order half-linear differential equations with several neutral terms[J]. Journal of Applied Mathematics and Computing, 2014, 44 (1/2): 511-518.

(责任编辑朱夜明)

doi:10.3969/j.issn.1000-2162.2016.04.005

收稿日期：2015-06-13

基金项目:国家自然科学基金青年科学基金资助项目(61503171)；辽宁省教育厅科研项目(L2013500)

作者简介：于强(1969-), 男, 辽宁丹东人, 辽东学院讲师.

中图分类号：O175.7

文献标志码:A

文章编号:1000-2162(2016)04-0022-08

Oscillation analysis of second-order nonlinear variable delay neutral differential equations

YU Qiang1, YANG Jiashan2

(1. Mathematical Department of Normal School, Eastern Liaoning University, Dandong 118003, China;2. School of Information and Electronic Engineering, Wuzhou University, Wuzhou 543002, China)

Abstract:We studied the oscillatory behavior of a class of second-order neutral functional differential equations with variable delay in this paper. By using the generalized Riccati transformation and some necessary analytic techniques, we established two new oscillation criteria and two comparison theorems for the oscillation of the equations. Those criteria improved and generalized some corresponding known results. Two examples were provided to illustrate assumptions in our theorems are less restrictive.

Keywords:oscillation; variable delay; functional differential equation; Riccati transformation