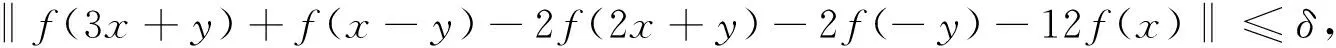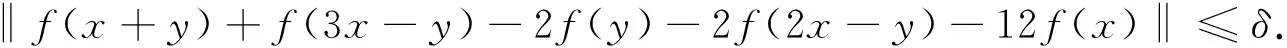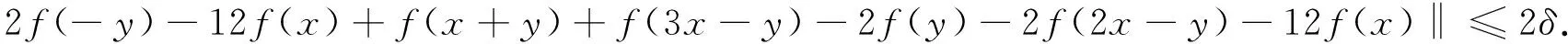Euler-Lagrange型三次泛函方程的稳定性问题

成立花

(西安工程大学 理学院,陕西 西安　710048)



Euler-Lagrange型三次泛函方程的稳定性问题

成立花

(西安工程大学 理学院,陕西 西安710048)

摘要:首先给出Banach空间中Euler-Lagrange 型三次泛函方程的一种新表示方法f(x+y-2z)+f(y+z-2x)+f(z+x-2y)+6f(x+y+z)=9[f(x+y)+f(y+z)+f(z+x)]-18[f(x)+f(y)+f(z)];其次证明6个泛函方程的等价性问题;最后利用不动点的择一性研究了Euler-Lagrange型三次泛函方程的存在性和稳定性问题.

关键词:广义Hyers-Ulam-Rassias 稳定性；不动点的择一性；三次泛函方程

泛函方程的稳定性问题源自Ulam[1]:“近似泛函方程的附近是否有真正的泛函方程?”.1941年,Hyers[2]解决了Banach空间上可加映射的稳定性问题;1978年, Rassias[3]给出了线性映射在Banach空间的稳定性问题;在接下来的几十年里,许多数学家对各种不同的泛函方程的不同稳定性进行了系统的研究,例如指数方程、二次泛函方程、三次泛函方程以及广义可加的泛函方程等[4-8],以及多种不同的稳定性问题[5-9].Jun等[5]在文章中介绍了如下的三次泛函方程及其稳定性问题

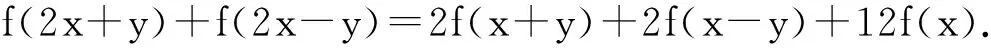
(1)

Park等[6]又引入了另一种形式的三次方程

(2)

Abbas等[7]介绍了下面的Euler-Lagrange型立方泛函方程

(3)

容易看出,(3)是(1)、(2)的推广.

2007年, Checkǎdariu等[8]概括性地给出了n次泛函方程的表达式

(4)

随后, Abbas等[9]又介绍了如下的三次泛函方程

3f(x+3y)+f(3x-y)=15f(x+y)+15f(x-y)+80f(x).

(5)

并且给出上述泛函方程的广义Hyers-Ulam-Rassias稳定性.其后,Jun等[10]证明了泛函方程(1)，(2)和(3)是等价的.其后,众多的研究者考虑借助不动点定理来证明各种泛函方程的稳定性[11-16]. 在前人研究的基础上,论文将提出以下具有轮换对称性的三次立方泛函方程

f(x+y-2z)+f(y+z-2x)+f(z+x-2y)=

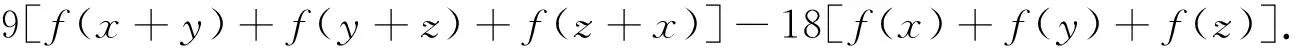
(6)

首先,将统一参考文献中关于三次泛函方程的描述,证明上述的6个泛函方程的等价性问题;其次,使用不动点的择一性给出方程(1)的Euler-Lagrange型三次泛函方程的稳定性问题.

1方程(1)～(6)的等价性问题

假设X,Y都是实向量空间,以下证明泛函方程(1)～(6)的等价性问题.

定理1设X,Y均为实向量空间,设映射f:X→Y,则以下结论等价

(i)f满足泛函方程(2).

(ii)f满足泛函方程(4).

(iii)f满足泛函方程(5).

(iv)f满足泛函方程(6).

(v) 存在函数B:X×X×X→Y,使得对于所有的x∈X,有f=B(X,X,X).且有当固定一个变量时函数B具有对称性,当固定两个变量时函数B具有可加性.

证明除(4)外,其他泛函方程都容易验证以下的性质:f(-x)=-f(x),x∈X,以及f(2x)=8f(x),3f(3x)=81f(x),f(ax)=a3f(x),a∈Z.以下证明上述结论间的等价性

(iv)⟹(i).在(6)中令(x,y,z)=(x,y,-y),有

(7)

在(7)中令x=3x,得到

(8)

再利用泛函方程f的性质:f(ax)=a3f(x),整理得到

(9)

泛函方程两边同除以常值9,并整理可得到泛函方程(2).

(i)⟹(iv).假设映射f:X→Y满足(2),由于文[10]中证明了(1),(2)和(3)的等价性,于是,在(1)中分别令(x,y)=(x+y,2z),(y+z,2x),(z+x,2y),可得到以下泛函方程

(10)

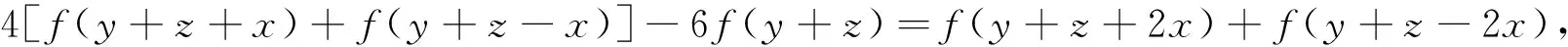
(11)

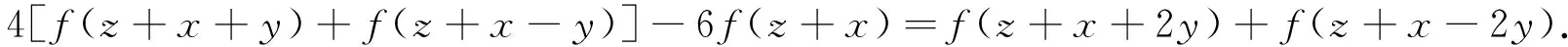
(12)

再在(1)中分别令(x,y)=(x,y+z),(y,z+x),(z,x+y),得到以下泛函方程

f(2x+y+z)+f(2x-y-z)=2f(x+y+z)+2f(x-y-z)-12f(x),

(13)

f(2y+z+x)+f(2y-z-x)=2f(y+z+x)+2f(y-z-x)-12f(y),

(14)

f(2z+x+y)+f(2z-x-y)=2f(z+x+y)+2f(z-x-y)-12f(z).

(15)

最后,在(2)中令(x,y)=(x+y,3z),在(1)中分别令(x,y)=(z,x+y+z),(x+y-z,2z),得到以下泛函方程

f(3z+x+y)+f(z-x-y)=2f(2z+x+y)-2f(x+y)+12f(z),

整理得到

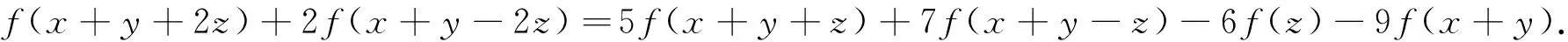
(16)

在(15)中分别令(x,y,z)=(y,z,x),(z,x,y),可以得到另外的两个泛函方程

f(y+z+2x)+2f(y+z-2x)=5f(y+z+x)+7f(y+z-x)-6f(x)-9f(y+z),

(17)

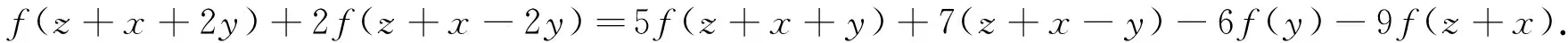
(18)

在上述泛函方程(10)～(18)中消去f(x+y+2z),f(z+x+2y),f(y+z+2x),f(y+z-x),f(x+y-z),f(z+x-y),即可得到泛函方程(6).

(i)⟹(iii).在方程(2)中用3y代替y,可得

然后交换变量x,y得f(3x+y)-f(3x-y)=9f(x+y)-9f(x-y)-16f(y).将上式和式(2)相加,有

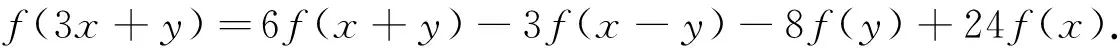
(19)

分别在上式中令(x,y)为 (y,x)和(x,-y),有

(20)

(21)

(20)式左右两侧同时乘以常数3, 然后再相加上(21)式即得方程(5).

(iii)⟹(i).在(5)中分别用 (y,x)和(x,-y)去替换(x,y),得到

3f(x+3y)-f(x-3y)=15f(x+y)-15f(x-y)+80f(x),

(22)

3f(x-3y)-f(x+3y)=15f(x-y)+15f(x+y)+80f(x).

(23)

整理可得到(19).在(19)中,用-y去替代y,有(21), 与(19) 相加即得方程(2).

(i)⟹(ii).在方程(19)中令y=-x-y, 结合(1),有

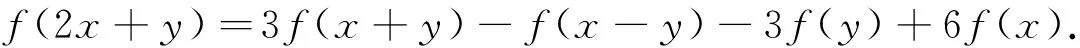
(24)

(19)加上(24)的-3倍, 有

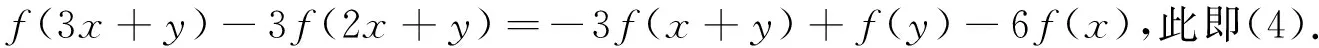
(ii)⟹(i).在方程(4)中令y=-2x+y,有

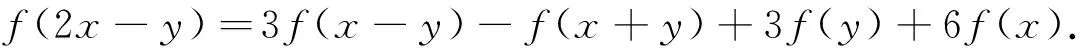
(25)

再次在(25)中令y=-x, 整理即得方程(1). 由于(1)、(2)和(3)的等价性,定理得证.

2方程(1)的稳定性问题

下面利用不动点定理给出三次泛函方程(1)的稳定性问题.

定理2[10]假设(Ω,d)为一个完备的广义度量空间,T:Ω→Ω是一个具有利普希茨常数L的严格压缩映射,对于任意的x∈Ω,下列之一成立

(1) ∀n≥0,d(Tnx,Tn+1x)=∞.

(2) 存在n0∈N,使得当n>n0时,d(Tnx,Tn+1x)<∞,且有

(a) 序列{Tnx}收敛于T的不动点y*;

(b)y*是集合Δ={y∈Ω:d(Tn0,x)<∞}中的关于映射T的唯一不动点;

设X,Y均为Banach空间,对于映射f:X→Y,∀x,y∈X,令

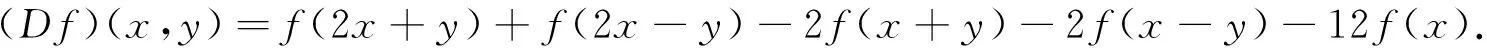
则有定理3成立.

定理3设映射f:X→Y满足f(0)=0,映射φ:X×X→(0,+∞)满足

(26)

且有

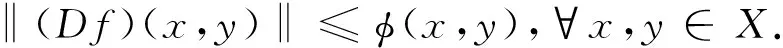
(27)

如果存在0≤L<1, 使得

(28)

那么存在唯一的三次映射V:X→Y满足

(29)

证明考虑集合Ω={g:X→Y|g(0)=0},并引入Ω上的广义度量

d(g,h)=inf{K∈(0,+∞]:‖g(x)-h(x)‖≤Kφ(x,0),∀x∈X}.

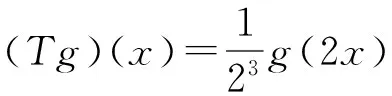
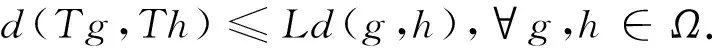
(30)

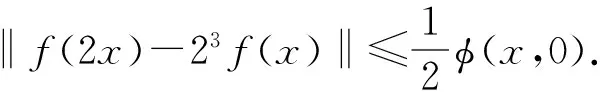
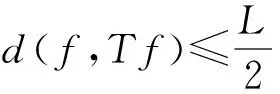
于是由定理2知,在Ω中存在算子T的不动点V,使得

因此,对于任意的ε>0,∃N>0,使得当n≥N时,有d(Tnf,V)<ε.所以,有

因而

(31)

在(27)中,分别令x=2nx,y=2ny,且两边同除以常值23n,则由(30)和(31),有

下证唯一性:设V1:X→Y是另外一个的三次映射,且满足条件

显然,TV1=V1,且V1∈Δ:={g∈Ω|d(f,g)<+∞}.由定理2知:V是T在集合Δ中的唯一的不动点.所以有V1=V.

类似定理3可证明定理4.

定理4设映射f:X→Y满足f(0)=0,且有

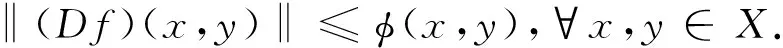
(32)

如果存在0≤L<1, 使得

(33)

且φ:X×X→(0,+∞)满足

那么存在唯一的三次映射V:X→Y满足

(34)

由以上定理3、4,可得到推论1～4.

推论1设s={1,-1}, 映射f:X→Y满足f(0)=0,且有

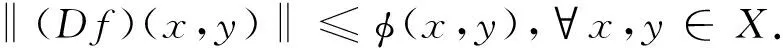
如果存在0≤L<1, 使得

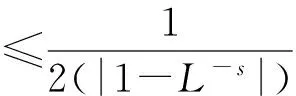
推论2设X是实赋范空间,0

则存在唯一的三次映射V:X→Y满足

证明设φ(x,y)=δ+ε‖x‖p+θ‖y‖q,∀x∈X.有

推论3设δ,p,q都是非负实数,且满足p+q∈(0,3),假设对于任意的x,y∈X,映射f:X→Y满足‖(Df)‖≤δ‖x‖p‖y‖q,则映射f是三次立方泛函方程.特别地,当固定变量x时,假若映射T:R→Y是连续的,则对于任意的t∈R,x∈X,有T(tx)=t3T(x).

假设f为从空间X到空间Y的映射,对于非负整数m,定义如下映射

证明在泛函方程(1)中分别令y=y+x和y=y-x,则可以分别得到两个不等式

两个不等式相加即有如下的不等式

于是有

假设‖(Dfm-1)‖≤δm-2,‖(Dfm)‖≤δm-1.类似由上面的分析,有

因此,有

参考文献：

[1]ULAM S M. A collection of mathematical problems[M].New York: Interscience Publishers, 1960.

[2]HYERS D H. On the stability of the linear functional equation[J]. Proc Nat Acad Sci (USA), 1941, 27 (4): 222-224.

[3]RASSIAS T M. On the stability of the linear mapping in Banach[J]. Proceedings of the American Mathematical Society, 1978, 72 (2): 297-300.

[4]BADORA R. On approximate ring homomorphisms[J]. J Math Anal Appl, 2002, 276: 589-597.

[5]JUN K, KIM H. The generalized Hyers-Ulam-Rassias stability of a cubic functional equation[J]. J Math Anal Appl, 2002, 274: 867-878.

[6]PARK K H, JUNG Y S. Stability of a cubic functional equation on groups[J]. Bull Korean Math Soc, 2004, 41 (2): 347-357.

[7]ABBAS N, MORADLOU F. Stability of an Euler-Lagrange type cubic functional equation[J]. Bull Korean Math Soc Turk J Math, 2009, 33 (1): 65-73.

[9]ABBAS N. Hyers-Ulam-Rassias stability of a cubic functional equation[J]. Bull Korean Math Soc, 2007, 44 (4): 825-840.

[10]JUN K H, CHANG I. On the Hyers-Ulam-Rassias stability of an Euler-Lagrange type cubic functional equation[J]. J Compur Anal Appl, 2005, 7 (1): 21-33.

[11]RASSIAS J M, KIM H M. Generalized Hyers-Ulam stability for additive functional equations in quasi-beta-normed spaces[J]. J Math Anal Appl, 2009, 356 (1): 302-309.

[12]TOBER J. Stability of cauchy functional equation in quasi-Banach spaces[J]. Ann Polon Math, 2004, 83: 243-255.

[13]ESKANDANI G Z, GAVRUTA P. Hyers-Ulam-Rassias stability of Pexiderized Cauchy functional equation in 2-Banach spaces[J]. J Nonlinear Sci Appl, 2012, 5: 459-465.

[14]YOUSSEF M, ELHOUCIEN E, RASSIAS T M. Hyers-Ulam stability of the Jensen functional equation in quasi-Banach spaces[J]. Nonl Func Anal Appl, 2010, 15 (4): 581-603.

[15]PARK C. Fixed points and stability of an AQCQ-functional equation in non-archimedean normed space[J]. Abstract and Applied Analysis, 2010 (1): 1-15.

[16]RAVI K, KODANDAN R. Stability of additive and quadratic functional equation in non-Archimedean spaces[J]. International Review of Pure and Applied Mathematics, 2010, 6 (1): 149-160.

(责任编辑朱夜明)

doi:10.3969/j.issn.1000-2162.2016.04.002

收稿日期：2015-07-03

基金项目:国家自然科学基金资助项目(11101323)；陕西省科技厅自然科学基金资助项目(2016JQ1029)

作者简介：成立花(1973-),女,陕西西安人,西安工程大学副教授．

中图分类号：O175.25

文献标志码:A

文章编号:1000-2162(2016)04-0006-06

Stability of the Euler-Lagrange type cubic functional equation

CHENG Lihua

(College of Science,Xi’an Polytechnic University, Xi’an 710048, China)

Abstract:Firstly, the new Euler-Lagrange type cubic functional equation f(x+y-2z)+f(y+z-2x)+f(z+x-2y)+6f(x+y+z)=9[f(x+y)+f(y+z)+f(z+x)]-18[f(x)+f(y)+f(z)] in Banach spaces was investigated. Secondly, equivalence of six functional equations was discussed. Lastly, by using the fixed pointed alternative, the general solution to the above functional equation was given and the stability of cubic functional equation was proved.

Keywords:generalized Hyers-Ulam-Rassias stability; fixed pointed alternative; cubic functional equation