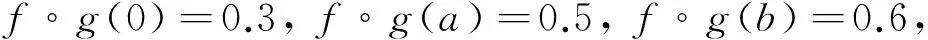BL-代数的(∈,∈∨q)-模糊理想

杨永伟,贺鹏飞,辛小龙

(1.安阳师范学院 数学与统计学院,河南 安阳　455000; 2.西北大学 数学学院,陕西 西安　710127)



BL-代数的(∈,∈∨q)-模糊理想

杨永伟1,2,贺鹏飞2,辛小龙2

(1.安阳师范学院 数学与统计学院,河南 安阳455000; 2.西北大学 数学学院,陕西 西安710127)

摘要:在BL-代数中引入了(∈,∈∨q)-模糊理想的概念, 给出了(∈,∈∨q)-模糊理想的性质和等价刻画； 然后, 通过模糊积和模糊上集概念的引入, 给出了(∈,∈∨q)-模糊理想的一个新的等价刻画； 最后, 在模糊陪集的基础上构造了商BL-代数.

关键词:BL-代数;模糊集;(∈,∈∨q)-模糊理想;模糊积;模糊上集

BL-代数是Hájek[1]在1998年提出的与基于连续三角模的Basic Logic相对应的代数结构. 滤子和理想理论作为研究各种代数结构和逻辑系统的有效工具[2-3], 对于BL-代数的理论研究起着重要的作用[4-6]. Liu等[7]将模糊集理论[8]应用到BL-代数中引入了模糊滤子的概念, 使得BL-代数在模糊化方面得到了迅速发展[9-10]. 利用模糊点与模糊子集“属于”和“拟重于”的概念, 相关文献提出并研究了(∈,∈∨q)-模糊滤子等概念[11-14], 使得BL-代数在模糊化方面的研究进入了一个新阶段. BL-代数由于缺少合适的加运算使其理想理论的研究受到了一定的限制, 为了解决这一问题, Lele等[15]通过伪加运算给出了理想的概念, 并获得一些重要的结果. 在BL-代数上,笔者将模糊点与模糊子集“属于”和“拟重于”的概念应用到理想理论中, 引入并讨论了(∈,∈∨q)-模糊理想, 然后给出了(∈,∈∨q)-模糊理想的性质和等价刻画.同时,还引入了模糊积和模糊上集的概念, 并借助它们给出了(∈,∈∨q)-模糊理想的一个等价刻画. 最后, 通过模糊陪集的构造, 给出了商BL-代数的概念.

1预备知识

定义1[1]一个(2,2,2,2,0,0)型的代数结构(L,∧,∨,⊗,→,0,1)称为BL-代数, 若它满足以下条件: ∀x,y,z∈L,(BL-1) (L,∧,∨,0,1)是有界格,有

(BL-2) (L,⊗,1)是可换幺半群;

(BL-3)x⊗y≤z当且仅当x≤y→z;

(BL-4)x⊗(x→y)=x∧y;

(BL-5) (x→y)∨(y→x)=1.

在接下来的讨论中, 若无特殊声明,L始终表示一个BL-代数.

引理1[1,4-6]若(L,∧,∨,⊗,→,0,1)是BL-代数, 则∀x,y,z∈L,有

(2)x⊗(x→y)≤y,x⊗y≤x∧y,x≤y→x, 1→x=x,x→1=1;

(3)x→(y→z)=(x⊗y)→z=y→(x→z), (x→y)→(x→z)≤x→(y→z);

(4) 若x≤y, 则x⊗z≤y⊗z,y→z≤x→z和z→x≤z→y;

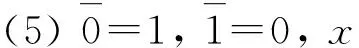
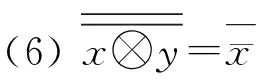
Lele和Nganou在L上定义伪加运算x其中:x,y∈L,给出了理想的定义.

定义2[15]设I是L的一个非空子集. 若I满足条件: ∀x,y∈L,有

(i)x,y∈I蕴含xy∈I;

(ii)x≤y和y∈I蕴含x∈I, 则称I为L的理想.

定义3[8]设f是非空集合X到单位闭区间[0,1]的映射, 即f:X→[0,1], 则称f是X上的一个模糊集. 记X上的所有模糊集构成的集合为F(X).

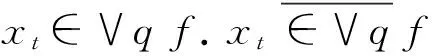
定义5[16]设f∈F(L), 若f满足条件: ∀x,y∈L, (1)f(xy)≥f(x)∧f(y); (2)x≤y蕴含f(x)≥f(y), 则称f是L的模糊理想.

定理1[17]设f∈F(L), 则f是L的模糊理想当且仅当∀x,y∈L, (1)f(0)≥f(x); (2)f(x)≥f(y)∧f(xy).

2(∈,∈∨q)-模糊理想

定义6设f∈F(L). 称f是L的(∈,∈∨q)-模糊理想, 若f满足下列条件: ∀x,y∈L,s,t∈[0,1],有

(I1) 若xs∈f,yt∈f, 则(xy)s∧t∈∨qf;

(I2) 若x≤y,yt∈f, 则xt∈∨qf.

定理2设f∈F(L), 则f是L的(∈,∈∨q)-模糊理想当且仅当∀x,y∈L,有

(F1)f(xy)≥f(x)∧f(y)∧0.5;

(F2) 若x≤y, 则f(x)≥f(y)∧0.5.

证明(必要性) 设f是L的(∈,∈∨q)-模糊理想. 首先证明(I1)⟹ (F1). 假设存在x,y∈L，使得f(xy)

(充分性) (F1)⟹ (I1). 设x,y∈L,s,t∈[0,1]. 若xs∈f,yt∈f, 则f(x)≥s,f(y)≥t. 根据(F1),有f(xy)≥f(x)∧f(y)∧0.5≥s∧t∧0.5. 当s∧t>0.5时,有f(xy)≥0.5, 故f(xy)+(s∧t)>1. 当s∧t≤0.5时, 则有f(xy)≥s∧t. 因此, (xy)s∧t∈∨qf.

(F2)⟹ (I2). 设t∈[0,1],x,y∈L且x≤y. 若yt∈f, 则f(y)≥t. 由(F2)知,f(x)≥f(y)∧0.5. 当t>0.5时, 则f(x)≥0.5, 从而f(x)+t>1. 当t≤0.5时, 则f(x)≥t, 因此,xt∈∨qf. 故f是L的(∈,∈∨q)-模糊理想.

定理3设f∈F(L), 则f是L的(∈,∈∨q)-模糊理想当且仅当∀t∈(0,0.5],L(f,t)(≠Ø)是L的理想.

证明(必要性) 设f是L的(∈,∈∨q)-模糊理想. ∀t∈(0,0.5], 若L(f,t)非空, 则对任意的x,y∈L(f,t), 有f(x)≥t,f(y)≥t, 即xt∈f,yt∈f. 由(F1)知,f(xy)≥f(x)∧f(y)∧0.5≥t∧t∧0.5=t, 因此,xy∈L(f,t). 设x,y∈L且x≤y. 若y∈L(f,t), 则f(y)≥t, 即yt∈f. 因为f(x)≥f(y)∧0.5≥t∧0.5=t, 所以x∈L(f,t). 根据定义2知,L(f,t)是L的理想.

(充分性) ∀t∈(0,0.5], 设L(f,t)(≠ø)是L的理想. ∀x,y∈L, 记t0=f(x)∧f(y)∧0.5, 则x∈L(f,t0),y∈L(f,t0). 因此,xy∈L(f,t0), 即f(xy)≥t0=f(x)∧f(y)∧0.5. 设x,y∈L且x≤y. 记s0=f(y)∧0.5, 则y∈L(f,s0). 根据定义2知,x∈L(f,s0), 故f(x)≥s0=f(y)∧0.5. 因此,f是L的(∈,∈∨q)-模糊理想.

定理4设f∈F(L), 则∀t∈(0.5,1],L(f,t)(≠Ø)是L的理想当且仅当∀x,y∈L,有

(1)f(xy)∨0.5≥f(x)∧f(y);

(2) 若x≤y, 则f(x)∨0.5≥f(y).

证明(必要性) ∀t∈(0.5,1], 设L(f,t)(≠Ø)是L的理想. 假设存在x,y∈L，使得f(xy)∨0.5

(充分性) 设条件(1)和(2)成立. 任取t∈(0.5,1], 若L(f,t)非空. 对任意的x,y∈L(f,t), 则0.5

定理5设f∈F(L), 则f是L的(∈,∈∨q)-模糊理想当且仅当f满足下列条件: ∀x,y∈L,有

(1)f(0)≥f(x)∧0.5;

(2)f(x)≥f(y)∧f(xy)∧0.5.

证明(必要性) 设f是L的(∈,∈∨q)-模糊理想. ∀x,y∈L, 则x≤y(xy). 由定理2知,f(x)≥f(y(xy))∧0.5≥f(y)∧f(xy)∧0.5. ∀x∈L, 因为0≤x, 所以,f(0)≥f(x)∧0.5.

(充分性) 设x,y∈L. 若x≤y, 则xy=0, 故f(x)≥f(y)∧f(xy)∧0.5=f(y)∧f(0)∧0.5=f(y)∧0.5.由于(xy)x≤y, 则f((xy)x)≥f(y)∧0.5. 又因为f(xy)≥f(x)∧f((xy)x)∧0.5≥f(x)∧f(y)∧0.5, 所以f是L的(∈,∈∨q)-模糊理想.

定理6设f∈F(L), 则f是L的(∈,∈∨q)-模糊理想当且仅当∀x,y,z∈L, 若z≤xy, 则f(z)≥f(x)∧f(y)∧0.5.

证明(必要性)f是L的(∈,∈∨q)-模糊理想. ∀x,y,z∈L, 若z≤xy, 根据定理2，知f(z)≥f(xy)∧0.5≥f(x)∧f(y)∧0.5.

(充分性) ∀x∈L, 因为0≤xx, 所以f(0)≥f(xx)∧0.5≥f(x)∧0.5. ∀x,y∈L, 由于x≤y(xy), 故f是L的(∈,∈∨q)-模糊理想.

定义7设f,g∈F(L), 定义L上的模糊集f∘g和f⊥分别为: ∀x∈L,(f∘g)(x)=sup{f(y)∧g(z)|x=yz, 其中y,z∈L},f⊥(x)=sup{f(y)|x≤y,其中y∈L},则称f∘g为f与g的模糊积,f⊥为f的模糊上集.

例1设(X,∧,∨,⊗,→,0,1)为例1所定义的BL-代数. 定义X的模糊集f和g分别为

f(0)=0.3,f(a)=0.5,f(b)=0.7,f(1)=0.2;g(0)=0.6,g(a)=0.8,g(b)=0.5,g(1)=0.4.

定义模糊集f∘g和f⊥分别为

则易验证f∘g是f与g的模糊积,f⊥为f的模糊上集.

定义8设f,g∈F(L). 对任意的x∈L,t∈(0,1], 若xt∈f有xt∈∨qg, 则称f拟小于g, 记为f≤∨qg.

定理7设f,g∈F(L), 则f≤∨qg当且仅当∀x∈L,g(x)≥f(x)∧0.5.

定理8设f∈F(L), 则f是L的(∈,∈∨q)-模糊理想当且仅当 (1)f∘f≤∨qf; (2)f⊥≤∨qf.

证明(必要性) 设f是L的(∈,∈∨q)-模糊理想. ∀x∈L, (f∘f)(x)∧0.5=sup{f(y)∧f(z)|x=yz}∧0.5=sup{f(y)∧f(z)∧0.5|x=yz}≤sup{f(yz)|x=yz}=f(x), 因此, (1) 成立.f⊥(x)∧0.5=sup{f(y)|x≤y}∧0.5=sup{f(y)∧0.5|x≤y}=sup{f(x)|x≤y}=f(x), 因此, (2) 成立.

(充分性)∀x,y∈L, 则f(xy)≥(f∘f)(xy)∧0.5=sup{f(x′)∧f(y′)|xy=x′y′}∧0.5≥f(x)∧f(y)∧0.5. 若x≤y, 则f(x)≥f⊥(x)∧0.5=sup{f(y′)|x≤y′}∧0.5≥f(y)∧0.5. 因此,f是L的(∈,∈∨q)-模糊理想.

设I是L的子集, 定义L的模糊子集χI为:χI(x)≥0.5,x∈I;χI(x)=0,x∈LI.

定理9设I是L的子集, 若I是L的理想, 则χI是L的(∈,∈∨q)-模糊理想.

证明根据χI的定义知,I=L(χI,0.5). 由于I是L的理想, 根据定理3容易证明χI是L的(∈,∈∨q)-模糊理想.

定理10设f∈F(L), 若f是L的(∈,∈∨q)-模糊理想, 则f*:={x∈L|f(0)=f(x)∧0.5}是L的理想.

定义9设f是L的(∈,∈∨q)-模糊理想,a∈L, 定义L的模糊子集a⨁f为: ∀x∈L,有

(a⨁f)(x)=f(ax)∧f(xa)∧0.5,

则称a⨁f为f的模糊陪集.

定理11设f是L的(∈,∈∨q)-模糊理想. ∀a,b∈L,则a⨁f=b⨁f当且仅当

f(ab)∧0.5=f(ba)∧0.5.

证明(必要性) 设a⨁f=b⨁f. 则(a⨁f)(a)=(b⨁f)(a), 即f(aa)∧f(aa)∧0.5=f(0)∧0.5=f(ba)∧f(ab)∧0.5. 注意到f是L的(∈,∈∨q)-模糊理想, 对任意的x∈L,有

f(0)∧0.5≥f(x)∧0.5.

(充分性) 根据引理1容易证明,对任意的x∈L,有xb≤(ab)(xa)和bx≤(ax)(ba). 又由于f是L的(∈,∈∨q)-模糊理想, 则f(xb)≥f(ab)∧f(xa)∧0.5和f(bx)≥f(ax)∧f(ba)∧0.5. 因此, (b⨁f)(x)=f(bx)∧f(xb)∧0.5≥f(ab)∧f(ba)∧f(xa)∧f(ax)∧0.5≥f(xa)∧f(ax)∧0.5=(a⨁f)(x), 故a⨁f≼b⨁f. 类似可证b⨁f≼a⨁f, 因此a⨁f=b⨁f.

设f是L的(∈,∈∨q)-模糊理想, 记L/f={x⨁f|x∈L}. 在L/f上定义运算: ∀a,b∈L,有

(a⨁f)(b⨁f)=(a⊗b)⨁f,(a⨁f)⇀(b⨁f)=(a→b)⨁f,

则容易证明定理12.

参考文献：

[2]杨闻起. BCI-代数的滤子[J]. 安徽大学学报(自然科学版), 2013, 37 (2):15-18.

[3]孟彪龙, 王伟. BE-代数的一类新的广义模糊理想[J]. 西北大学学报(自然科学版), 2012, 42 (5): 705-708.

[4]TURUNEN E. BL-algebras of basic fuzzy logic[J]. Mathew Soft Comput, 1999, 6 (1): 49-61.

[5]HAVESHKI M, SAEID A B, ESLAMI E. Some types of filters in BL algebras[J]. Soft Comput, 2006, 10 (8): 657-664.

[6]SAEID A B, MOTAMED S. Some results in BL-algebras[J]. Math Log Quart, 2009, 55 (6): 649-658.

[7]LIU L, LI K. Fuzzy filters of BL-algebras[J]. Inform Sci, 2005, 173 (1): 141-154.

[8]ZADEH L A. Fuzzy sets[J]. Inform Control, 1965, 8 (3): 338-353.

[9]薛占熬, 肖运花, 薛天宇, 等. BL-代数上的几种直觉模糊滤子[J]. 计算机科学, 2012, 39 (2): 198-201, 219.

[10]WANG W, XIN X L. On fuzzy filters of pseudo BL-algebras[J]. Fuzzy Sets and Systems, 2011, 162 (1): 27-38.

[11]MA X, ZHAN J. On (∈, ∈∨q)-fuzzy filters of BL-algebras[J]. Jrl Syst Sci & Complexity, 2008, 21: 144-158.

[13]ZHAN J, XU Y. Some types of generalized fuzzy filters of BL-algebras[J]. Comput Math Appl, 2008, 56 (6): 1604-161.

[14]YANG Y W, XIN X L, HE P F. (∈γ, ∈γ∨qδ)-intuitionistic fuzzy (soft) filter of BL-algebras[J]. Chinese Quart J Math, 2014, 29 (1): 65-75.

[15]LELE C, NGANOU J B. MV-algebras derived from ideals in BL-algebras[J]. Fuzzy Sets and Systems, 2013, 218: 103-113.

[16]YIN Y, ZHAN J. Characterization of ordered semigroups in terms of fuzzy soft ideals[J]. Bull Malays Math Sci Soc, 2012, 35 (4): 997-1015.

[17]CELESTIN L, NGANOU J B. Pseudo-addition and fuzzy ideals in BL-algebras[J]. Annals of Fuzzy Mathematics and Informatics, 2014, 8 (2): 193-207.

(责任编辑朱夜明)

doi:10.3969/j.issn.1000-2162.2016.04.004

收稿日期：2015-05-25

基金项目:国家自然科学基金资助项目 (11571281);河南省高等学校重点科研项目(16A110028， 16A130004)

作者简介：杨永伟(1984-), 男, 河南柘城人, 安阳师范学院讲师, 博士.

中图分类号：O159

文献标志码:A

文章编号:1000-2162(2016)04-0017-05

(∈,∈∨q)-fuzzy ideals of BL-algebras

YANG Yongwei1, 2, HE Pengfei2, XIN Xiaolong2

(1.School of Mathematics and Statistics, Anyang Normal University, Anyang 455000, China;2.Shool of Mathematics, Northwest University, Xi’an 710127, China)

Abstract:The concept of (∈,∈∨q)-fuzzy ideals was proposed in BL-algebras, and some properties and characterizations of (∈,∈∨q)-fuzzy ideals were obtained. Then a new characterization of (∈,∈∨q)-fuzzy ideals was given by the notions of fuzzy products and fuzzy up-sets. Finally, quotient BL-algebras were constructed based on fuzzy cosets.

Keywords:BL-algebra; fuzzy set; (∈,∈∨q)-fuzzy ideal; fuzzy product; fuzzy up-set