基于改进遗传算法优化的混凝土坝坝基扬压力统计模型研究
2016-08-04游健
游 健
(云南省水利水电勘测设计研究院, 昆明 650000)
基于改进遗传算法优化的混凝土坝坝基扬压力统计模型研究
游健
(云南省水利水电勘测设计研究院, 昆明650000)
摘要:混凝土坝坝基扬压力是外界复合环境因素综合作用的结果,如何建立准确反应大坝实际渗流性态的统计模型对于掌握大坝安全性态具有十分重要的意义.本文基于外界环境量对混凝土坝坝基扬压力的影响过程分析,将前期库水位及降雨对坝基扬压力的非线性影响过程视为“正态分布”过程,并采用改进遗传算法对相应滞后天数和影响天数进行智能寻优,以提高坝基扬压力统计模型准确性.最后,以某混凝土坝为例,采用本文方法对其坝基扬压力实测进行拟合和预测,通过与传统统计模型对比,表明本文方法具有更高的拟合和预测精度,具有一定的科学和实践应用价值.
关键词:混凝土坝;坝基扬压力;统计模型;改进遗传算法
0引言
混凝土坝坝基扬压力安全监测是大坝安全监测的重要组成部分,研究表明坝高100m左右的重力坝,坝基面上作用的扬压力大约为坝体重量的20%左右[1].因此,如何建立反应混凝土大坝坝基实际渗流性态的扬压力统计模型对于掌握大坝安全工作性态具有十分重要的意义.姜谙男等基于支持向量机结构风险最小化原理,采用粒子群算法快速优化支持向量机模型参数,对大坝渗流监测资料进行非线性拟合,建立了基于PSO-SVM的人坝渗流监测的时间序列非线性预报模型[2].为了消除统计模型中各因子相关性对分析结果的影响,田伟等将主成分分析法和神经网络方法相结合,建立了大坝渗流监测数据的主成分神经网络模型[3].李波等采用最小二乘回归法对大坝渗流各因子进行筛选,提取对因变量影响强的成分,建立了基于PLS-LSSVM的大坝渗流监控模型,有效克服了变量间的多重相关性问题[4].梅一韬等利用物元可拓理论与模糊数学理论构造了渗流性态评价中的模糊物元,引入嫡权法确定大坝渗流指标体系的权重系数,建立了基于嫡权的模糊可拓评价模型[5].传统混凝土坝基扬压力统计模型将坝基扬压力视为与前期平均库水位及降雨量呈线性相关关系,然而大坝安全资料分析表明上游库水位及降雨对混凝土坝坝基扬压力的影响过程是一个先增长后下降的过程,而不是一个“平均”过程,因此需要进一步研究混凝土重力坝坝基扬压力统计模型的因子选择以提高模型准确性.
本文基于上游库水位及降雨对坝基扬压力的非线性影响过程,采用改进遗传算法以相应统计模型复相关系数为适应度值,对相应滞后天数和影响天数进行智能优化,从而提高统计模型精度.最后为了验证本文方法的有效性,以某混凝土重力坝为例,采用上述方法对其多年坝基扬压力进行拟合,通过与传统统计模型对比分析,表明本文方法具有更高的拟合和预测精度.
1基本理论
基于混凝土坝实测资料分析,本文混凝土重力坝坝基扬压力统计模型采用如下形式:
(1)
式中,P为坝基扬压力,PH为水压分量,PR为降雨分量,Pθ为时效分量,PT是温度分量.
1)水位分量PH.坝基扬压力是在库水位变动情况下非稳定渗流的瞬时状态结果,任意时刻的坝基扬压力是此时刻以前库水位连续变化影响的瞬态结果.传统统计模型将前期水位的平均值作为因子进行考虑(如图1所示),然而,监测资料分析表明,库水位对坝基扬压力的影响是一个先上升后下降的过程,基本服从“正态”分布过程(如图2所示)[6-7].不同于传统统计模型,本文考虑库水位对坝基渗流非线性影响的水压分量采用如下形式:
(2)
式中,aj为回归系数;x1为滞后天数;x2为影响天数;Hi(t)为上游水位;Hum为有效水位.
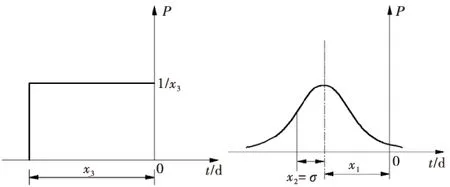
图1 前x3天平均水位 图2 正态分布影响曲线(P-影响权) (P-影响权)
其中,x1,x2需要通过试算求得,在求得准确滞后天数和影响天数后,即可提高相应统计模型拟合和预测精度.
2)降雨分量PR.降雨与大坝渗流的关系比较复杂,它与入渗条件、雨型、地质条件等因素有关,降雨量与大坝渗流呈现明显的非线性关系[8-9].基于此,采用指数关系法,把降雨量做2/5指数变化,变换后降雨量变化比较平稳,综合考虑降雨对大坝渗流的滞后影响过程,本文采用坝基扬压力降雨分量如下:
(3)
式中,bj为降雨分量的回归系数;x3为降雨分量的滞后天数;x4为降雨影响权正态分布标准差(影响天数);R(t)为t时刻的单位时段降雨量;Rum为有效降雨量.其中,x3和x4需要通过试算求得.
3)温度分量PT.混凝土坝基岩裂隙变化受基岩温度影响显著,而基岩温度变化基本呈年周期性变化规律,本文采用周期函数来描述温度分量:
(4)
式中,c1i,c2i为回归系数.
4)时效分量Pθ.时效分量是混凝土重力坝坝基扬压力的重要组成部分,也是评价大坝渗流稳定性的重要依据[10],将坝体测压管水位时效分量表示为:
(5)
式中,d1,d2为回归系数;θ为监测日自初始监测日天数除以100.
因此,本文定义的新型混凝土坝坝基扬压力统计模型如下:
(6)
2双链量子遗传算法
传统遗传算法(GA)采用二进制编码,该编码方式存在随机性,容易造成算法收敛速度慢、容易陷入局部极值等问题[11-13].基于此,本文采用双链量子遗传算法对相应统计模型的滞后天数和影响天数进行智能优化,其流程如图3所示.

图3 双链量子遗传算法流程图
该算法采用量子位概率幅值对染色体进行编码,每条染色体分别包括两个优化解,通过量子旋转门与量子非门来增加种群多样性,从而提高遗传算法的收敛速度与精度[14-15].
一个量子位可能处于0态、1态、以及|0〉和|1〉之间的任意叠加态.可以表示为:
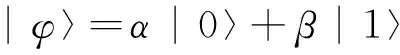
(7)
式中,α,β为相应量子位的概率幅值.|α|2为量子态达到|0〉态时相应的概率,|β〉2为量子态达到|1〉态的概率,并且满足归一化条件
(8)
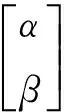
(9)
式中,θij=2π×rnd;rnd∈(0,1)为随机数;i=1,2,…,m,j=1,2,…,n,其中m为种群规模,n为空间维数.
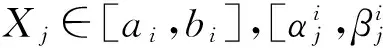
(10)
即可表示为:
(11)
式中,i=1,2,…,m,j=1,2,…,n.
量子门更新过程可以表示为:
(12)

(13)
所以,可以得出:
相应量子转角定义如下:
(14)

(15)
(16)
为了避免算法陷入局部极值,本文同时引入量子非门作为变异算子来增加种群多样性,相应量子染色体变异操作如下:
(17)
式中,[cosθijsinθij]T为编号i量子染色体|pi〉的第j个基因位.
3工程实例
3.1工程简介
某水电站位于福建省闽清县境内的闽江干流上,为了监测大坝渗流状况,掌握扬压力的变化规律,沿坝轴线方向设置一条纵向观测断面.在帷幕下游侧共设置了38个观测孔,沿纵向均匀分布.另外,根据坝基地质情况,在11号、17号、25号、32号坝段的横向观测廊道中,分别设4个扬压力观测孔[16].
3.2坝基扬压力分析
为验证本文双链量子遗传算法有效性,本文同时采用传统遗传算法进行计算,两种方法最优个体适应度值进化过程如图4所示.由图4可知,双链量子遗传算法最终复相关系数为0.961,而传统遗传算法最终复相关系数为0.935,双链量子遗传算法具有更高的计算效率和收敛精度.

图4 种群最优适应度值发展曲线
为验证本文方法有效性,本文同时采用多元非线性回归统计模型[1]对该测点测值进行拟合,相应统计模型为:
(18)
式中,c0为待求常数项,H(t),H(t-τn)分别为时刻t和计算时间前τn时间的水头,τn为滞后时间,w(t),w(t-i)分别为计算当日的降水量和计算时刻前i天内前期降水量的累加值,cij,αi,βi,a,b,di分别为待定系数.
通过采用多元非线性统计回归法,剔除影响因素不明显的因子,可得关于渗流监测效应量统计模型表达式,该方法可以克服传统统计模型只能针对单测点监测的缺点,相应两种方法拟合结果及两种方法拟合残差如图5~6所示.
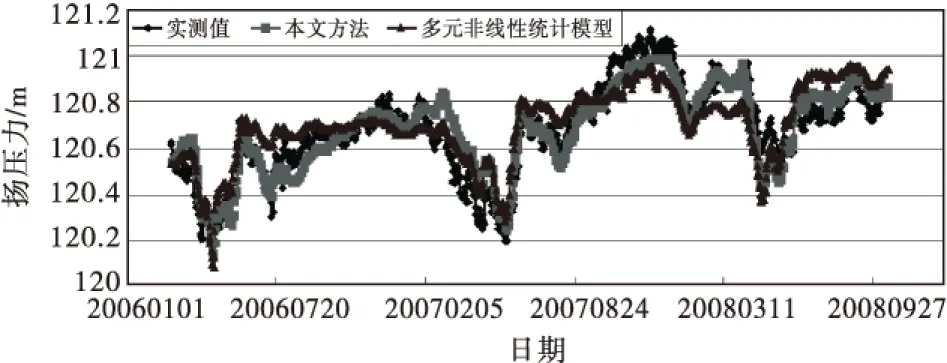
图5 传统方法拟合结果
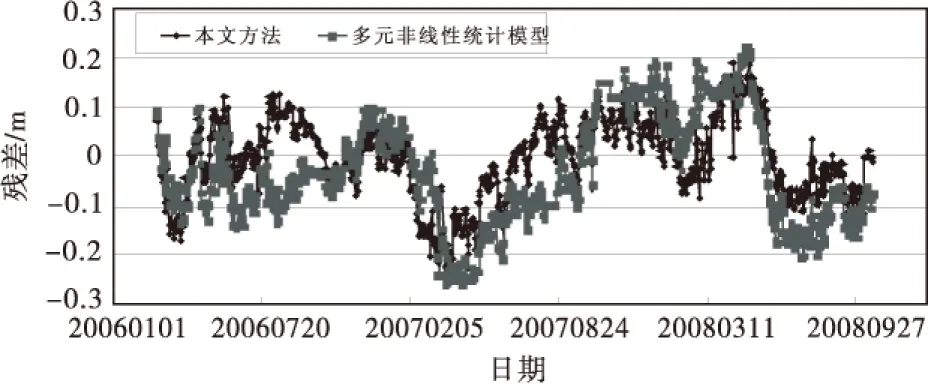
图6 传统方法拟合结果
由图可知,本文方法拟合结果与7号坝段坝蹱位置扬压力实测值接近,能够准确反映该测点坝基扬压力的变化规律.本文方法所得复相关系数为0.987,远大于多元非线性回归统计模型拟合结果0.945,具有更高的拟合精度.因此,本文方法能够准确反映前期库水位及降雨对混凝土坝基扬压力的非线性影响.
为了验证本文方法的预测精度,采用上述两种模型对该测点2008年10月20日至2008年10月31日之间扬压力测值进行预测,并与实测值对比,如图7所示.

图7 坝基扬压力预测结果对比图
由图可知,本文方法预测结果相比多元非线性统计模型具有更高的预测精度,此外,由于本文模型考虑了前期库水位及降雨对坝基扬压力测值的非线性影响,因此能够反映出坝基扬压力测值的非线性变化.
4结论
本文考虑上游库水位及降雨对混凝土坝坝基扬压力的非线性影响,将前期库水位及降雨对坝基扬压力的影响视为“正态分布”过程,并采用双链量子遗传算法对其进行智能优化,通过传统统计模型计算结果对比分析,可以得出如下结论:
1)双链量子遗传算法综合量子运算和遗传算法基本原理,采用量子概率幅值对染色体进行编码,利用量子门及量子非门对染色体进行实时更新,避免了传统遗传算法容易产生局部极值的现象,具有更高的计算效率和精度.
2)通过将上游库水位及降雨对坝基扬压力的影响视为“正态分布”过程,并采用改进遗传算法对相应滞后天数和影响天数进行智能寻优,相比传统统计模型具有更高的拟合精度.
3)由于本文模型能够准确反映前期库水位及降雨对坝基扬压力的非线性影响,因此本文模型相比传统统计模型能够准确预测坝基扬压力的变化趋势,具有更高的预测精度.
参考文献:
[1]顾冲时,吴中如.大坝与坝基安全监控理论和方法及其应用[M].南京:河海大学出版社,2006.
[2]姜谙男,梁冰.基于PSO-SVM的大坝渗流监测时间序列非线性预报模型[J].水利学报,2006,37(3):331-335.
[3]田伟,魏光辉,高强.基于主成分分析与BP神经网络模型的大坝渗流监测资料分析[J].大坝与安全,2009(5):29-31.
[4]李波,顾冲时,李智录,等.基于偏最小二乘回归和最小二乘支持向量机的大坝渗流监控模型[J].水利学报,2008,39(12):1390-1394.
[5]梅一韬,仲云飞.基于熵权的大坝渗流性态模糊可拓评价模型[J].水电能源科学,2011,29(8):58-61.
[6]刘耀儒,杨强,覃振朝.基于统计模型的裂隙岩体渗流场的并行数值模拟[J].岩石力学与工程学报,2008(4)::736-742.
[7]洪云,郑东键.古田溪一级大坝14号坝段以左的渗压确定性模型[J].水电自动化与大坝监测,1996(3):30-31.
[8]顾冲时,李波,徐宝松,等.碾压混凝土坝渗漏安全监控模型建模方法研究[J].河海大学学报:自然科学版,2008,36(5):579-585.
[9]胡江,郑鹏翔.基于滞后效应和防洪调度的大坝渗流预测模型研究[J].三峡大学学报:自然科学版,2008,30(6):16-19.
[10] 毕奇龙,刘星,徐波,等.因子分析法在绕坝渗流监测资料分析中的应用[J].水电能源科学,2010,28(5):62-65.
[11] 杨建文,李志鹏,喻哲欣.基于改进遗传算法的泵站优化运行[J].中国水利,2015(8):33-35.
[12] 张尚然,汤亚芳,林俐.基于改进遗传算法的无功优化方法的研究[J].中小企业管理与科技,2015(7):162-163.
[13] 邵改革,卢小平,杜耀刚,等.基于优化模糊遗传算法的地理信息个性化推送方法[J].测绘工程,2015,24(7):20-23.
[14] 夏俊,凌培亮,虞丽娟,等.基于量子遗传算法的无线传感网络路由优化[J].同济大学学报:自然科学版,2015,43(7):1097-1103.
[15] 沙林秀,贺昱曜,陈延伟.一种变步长双链量子遗传算法[J].计算机工程与应用,2012(20):59-63.
[16] 李延芳,王玉洁,赵花城.水口水电站大坝原型观测设计[J].水力发电,1994(6):23-25.
[责任编辑王康平]
DOI:10.13393/j.cnki.issn.1672-948X.2016.03.002
收稿日期:2015-11-17
基金项目:国家自然科学基金“静动结合的高拱坝健康性态监测和诊断方法研究”
通信作者:游健(1962-),女,高级工程师,主要研究方向为水工设计.E-mail:yannan_youjian@126.com
中图分类号:TV64
文献标识码:A
文章编号:1672-948X(2016)03-0006-05
Research on Statistical Model of Uplift Pressure Based on Improved Genetic Algorithm
You Jian
(Yunnan Provincial Conservancy & Hydropower Survey, Design Institute, Kunmin 650000, China)
AbstractThe variation of uplift pressure on concrete dam foundation is effected by the compound external environmental factors. How to establish statistical model which accurately reflects the real dam seepage state is quite important to grasp the safety state of a dam. Based on analyzing the influential process of ambient variables, the paper considers the nonlinear influential process as “Normal” process and adopts the improved genetic algorithm to optimize the lagged days and the influential days to raise the accuracy of the statistical model. Finally, taking a certain concrete dam for example, the recorded series of the uplift pressure is fitted and predicted with the proposed method. By comparing with the traditional model, it is verified that the proposed method possesses higher fitting and prediction accuracy and is of certain scientific and practical value.
Keywordsconcrete dam;foundation uplift pressure;statistical model;improved genetic algorithm
