褶皱冲断带构造砂箱物理模型研究进展
2016-08-04赵高平万元博王兴建刘树根
邓 宾, 赵高平, 万元博, 黄 瑞, 王兴建, 刘树根
(1.成都理工大学 油气藏地质及开发工程国家重点实验室, 四川 成都 610059; 2.成都理工大学 国土资源部构造成矿成藏重点实验室, 四川 成都 610059)
褶皱冲断带构造砂箱物理模型研究进展
邓宾1, 2, 赵高平1, 万元博1, 黄瑞1, 王兴建1, 刘树根1
(1.成都理工大学 油气藏地质及开发工程国家重点实验室, 四川 成都 610059; 2.成都理工大学 国土资源部构造成矿成藏重点实验室, 四川 成都 610059)
地壳浅层次褶皱冲断带普遍受控于具耦合互馈特性的多种机制或边界条件, 从而具有长期的构造演化过程和复杂的构造特征。自19世纪初以来, 基于地质构造过程自相似性和“无理有效性”的砂箱物理模型, 为解译褶皱冲断带的演化过程及其动力学机制等提供了独立有效的手段。本文主要基于国内外地壳浅表褶皱冲断带构造变形过程为研究对象的构造砂箱物理模型研究结果与进展进行综述性报道, 以期为同行提供参考与借鉴。基于与地壳浅表地层具相似流变学特性的砂箱物理模拟研究, 揭示出地壳浅层次构造变形过程普遍自相似性生长过程, 符合库伦临界楔理论。褶皱冲断带挤压变形过程中, 基底特性(基底几何学、有效摩擦角、基底耦合性和流体超压)、变形物质特性(空间几何学、能干层、流变学和非均一性)、动力学机制(砂箱几何边界、汇聚速率和汇聚方向)、浅表作用(剥蚀和沉降)等对于地壳浅表构造变形过程具有明显的控制作用。构造砂箱物理模型在解译不同构造变形过程与机制的研究中发挥着越来越突出的作用。
砂箱模型; 临界构造楔; 褶皱冲断带
0 引 言
自然界构造变形具有长时间的演化周期和复杂的结构构造特征, 普遍受多种因素影响, 如: 地层非均质性、几何学和运动学边界条件和浅部地表过程等, 从而难以有效量化、解译其在地史中的形成演化过程。地质构造过程的自相似性(标度不变性)和实验验证等说明物理模型模拟与自然界盆–山系统演化等具有一致性(无理的有效性“Unreasonable effectiveness”, Wigner, 1960), 即尺度大小上的相似性与一致性), 它是砂箱物理模型研究的理论基础。值得指出的是, 虽然砂箱构造物理模型有与生俱来的缺点, 如: 简化地层模型、流体压力–温度等缺失问题, 但它能够帮助我们在时间–空间上详细观察、解译构造变形的形成与生长四维过程, 因此受到越来越广泛的应用。
项目资助: 国家自然科学基金(41572111, 41402119, 2014JQ0057, 41472107, 41230313)和国家基础研究发展计划“973”项目(2012CB214805)联合资助。
自Hall (1815)初次使用构造物理模型解释苏格兰东海岸构造带褶皱变形以来, 砂箱模型相对于早期实验装置及其理论体系已经发生了极大的革新与变化。由于不同的目的性和手段性等差异, 砂箱模型目前主要存在三种典型类别: 构造砂箱模型(Tectonic sandbox modelling)以褶皱冲断带等生长变形机制为主要研究对象(Cadell, 1988), 地貌几何砂箱模型(Geomorphic sandbox modelling)以可控降水(量)条件下人工地貌为主要研究对象(Flint, 1973),地层砂箱模型(Stratigraphic sandbox modelling)以构造和/或气候条件下地层沉积记录为主要研究对象(Paola et al., 2009)。19世纪以来, 以砂箱模型为主的物理(和/或结合数字)模型手段广泛地运用于与增生楔和冲断带等相关的研究中, 结合库仑冲断楔(即临界楔理论“Critical taper theory”)共同揭示出四维时空尺度上砂箱模型的基底特性、变形物质特性、活动挡板(或阻挡物)特性、变形物质通量(输出和输入)、汇聚(挤压)运动学和地表过程等对盆–山结构–构造演化过程的重要作用(Bonini, 2003; Bonnet et al., 2007; Buiter, 2012; Graveleau et al., 2012; Koyi and Vendeville, 2003; Konstantinovskaia and Malavieille 2005; McClay et al., 2004, 2011)。本文主要基于国内外以褶皱冲断带构造变形为研究对象的构造砂箱物理模型研究结果与进展进行综述性报道,简要阐述不同构造变形过程中砂箱构造物理模型所揭示的变形过程和机制及其主要控制因素等, 以期为同行研究提供参考与借鉴。
1 临界楔理论与其自相似性生长过程
以褶皱冲断带为典型构造的造山带结构演化普遍遵循简单的变形机制即临界楔理论(图 1), Davis et al. (1983)和Dahlen (1990)描述为“移动推土机前方的楔形砂体”。推土机前方物质沿其底部滑脱面滑动挤压变形直到底部滑脱面倾角(β)和砂体顶面倾角(楔顶角, a)之间夹角恒定(即β+α恒定, 称为临界角),它主要受控于楔形体强度和基底特性。如果挤压形成的楔形体前方没有进一步的物质加积, 楔形砂体则沿底部滑脱面仅发生滑动位移; 如果楔形砂体前方发生进一步的物质加积, 楔形砂体则发生保持其几何特征(即临界角 β+a恒定)的自相似性生长过程。临界楔理论具有一定的假设前提(Dahlen, 1984): (1) 较低或可忽略的内聚力强度和符合Coulomb破裂准则; (2) 均值且各向同性的砂体特性; (3) 均值摩擦底界特性; (4) 砂箱物质和温度等属性不随时间变化。一般而言, 楔形体遵循如下公式:
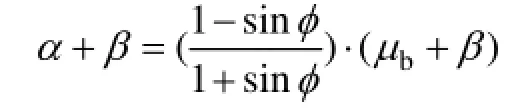

(a), (b) 张性和压性造山增生楔变形模型(Dahlen, 1990; Xiao et al., 1991); (c) 张性和压性增生楔形体临界楔理论值变化协和图(Mourgues et al., 2013), 其中①挤压楔形体中基底面剪切力朝向楔形体外部的临界稳态平衡状态(Davies et al., 1983); ②重力扩展或重力滑动临界稳态平衡状态(Mourgues et al., 2013); ③张性楔形体中基底面剪切力朝向楔形体内部的临界稳态平衡状态(Xiao et al., 1991)。图1 张性和压性体制临界楔理论综合示意图Fig.1 Synthetic diagram showing critical taper solutions for extensional and compressive sand wedges
式中, μb为基底摩擦系数, φ为砂箱物质内摩擦角。
临界楔理论揭示褶皱冲断带自相似性生长过程和其最终趋于稳态平衡演化的特征, 即造山楔形体物质输入、楔形体几何形态(楔顶角和基底倾角)、楔形体内部(包括流体压力)和基底摩擦力相关的应力机制等因素最终达到稳态平衡(Davis et al., 1983; Dahlen, 1984)。现今构造砂箱物理和数字模型不仅广泛验证了临界楔理论强调的基本推论, 如: 基底倾角(增大)和楔顶角(减小)相关性、前展式(倾角变陡)和反冲断层(倾角变小)以及楔形体(变宽)同基底强度(减小)之间的相关性、楔形体(变窄)与地表剥蚀作用(增强)相关性等, 而且对临界楔形体理论大大地进行了拓宽, 如: 非临界楔状态的褶皱冲断带、非均质性物质和应变弱化带等(McClay, et al., 2004; Willett et al., 2006; Suppe, 2007; Bigi et al., 2010; Buiter, 2012; Wenk and Huhn, 2013)。临界楔理论强调褶皱冲断带自相似生长过程主要受控于多个基本因素: 楔形体内部动力学、楔形体物质特性(如: 内聚力、密度、内摩擦系数和流体压力等)、基底特性(如: 几何学、摩擦角等)和地表作用过程。
一般而言, 褶皱冲断带挤压楔形体动态演化常具有三种端元: (1) 稳态平衡状态(阶段), 楔形体仅发生整体位于基底面上的稳定滑动、楔形体内部不发生构造变形(图1中空白区为稳态域), 其楔形体底部滑脱面倾角与楔顶角之和恒定; (2) 有限或临界稳态平衡状态(阶段), 楔形体内部和基底摩擦力相关的应力状态、楔形体后缘加载和内聚力等初步达到稳态平衡状态(图中实线或虚线), 楔形体以自相似性特征生长变形、维持临界角及其几何形态; (3)非稳态平衡状态(阶段), 楔形体通过构造变形调整其几何形态逐步达到临界稳态平衡状态, 如: 亚稳态状态缩短变形、超稳态状态张性变形(图1中阴影区)。亚稳定状态即楔形砂体顶面倾角相对于底部滑脱面过小, 砂体通过挤压变形相关的前缘加积、冲断等作用增加其顶面角(楔顶角), 达到临界稳态平衡状态,即褶皱冲断带建造过程。超稳定状态即楔形砂体顶面倾角相对于底部滑脱面过大, 砂体会发生张性正断层或滑动变形降低砂体顶面角, 最终达到临界稳态平衡状态, 即褶皱冲断带破坏过程。
临界楔理论静态地诠释造山楔恒定应力条件下的特征, 它已经成功地运用于解释褶皱冲断带几何学发展演化过程。基底摩擦角增大将会导致稳态平衡状态缩小(图中稳态域缩小), 即基底倾角范围增大和楔顶角范围减小, 也意味着早期非稳态状态域内的楔形砂体通过调整楔顶角大小获得稳态平衡状态。楔形砂体内摩擦强度增大和基底强度减弱相似,都会导致稳态平衡状态增大(图中稳态域增大), 即增大楔顶角范围。如果楔形砂体物质受剥蚀减少和增生加积平衡作用, 则会发生褶皱冲断带稳态造山作用(Willett and Brandon, 2002; Willett et al., 2006),但高剥蚀速率会导致楔形砂体或造山带规模减小(如: 台湾和新西兰地区), 而低剥蚀速率则导致其规模增大(如: 安第斯中央高原)。Willett and Brandon (2002)进一步强调褶皱冲断带稳态造山作用的四个典型类型, 即: 物质通量恒定、地貌稳态、热稳态和地表剥蚀作用稳态。在构造挤压变形过程中, 楔形体通过内部和外部构造变形调整其几何形态, 最终达到并保持稳态平衡状态, 即自相似性生长过程,其主要表现为通过楔形体内部冲断破裂变形的楔形体增厚过程与楔形体前缘扩展变形的楔形体增长过程二者周期性循环发生, 从而保持构造楔形体几何学的相似性(McClay and Whitehouse, 2004; Del Castello et al., 2004; Konstantinovskaia and Malavieille, 2005; Bigi et al., 2010)。
基于张性和挤压构造背景下楔形体具有相似褶皱冲断带、增生楔特征和相反的滑动基底和楔形体内变形特性, Xiao et al. (1991)初次对张性构造背景下楔形体变形进行了物理模拟, 认为张性楔形体变形过程是“移动推土机沿滑动面下倾方向运动的相关变形”, 也遵循临界楔理论(Morgan and McGovern, 2005)。当楔形砂体处于亚稳定状态, 将会通过沿基底倾向的滑动变形达到稳态平衡状态; 当楔形砂体处于超稳定状态, 将会形成正断层变形减小楔顶角达到稳态平衡状态。但是, 当张性楔形体中楔顶角小于临界值时, 它也可能处于稳态平衡状态, 不发生楔形砂体内部变形, 而与挤压构造背景下楔形砂体形成明显区别(Xiao et al., 1991)。最近, Mourgues et al. (2013)通过数值和砂箱模型实验, 揭示了张性构造背景下构造变形并不完全符合临界楔理论, 认为基底滑脱面流体压力比控制着张性构造楔形体形成演化(Mourgues and Cobbold, 2006), 导致其形成典型的浅部滑塌和深部(构造楔主滑脱面)重力扩展变形。当楔形砂体处于超稳定状态, 受控于楔形体内压力小于临界压力比砂体仅发生浅部滑塌变形,楔形体内压力大于临界压力比导致以主滑脱面变形相关的重力扩展作用, 且伴随流体压力比增大、楔顶角变小。
褶皱冲断带临界构造楔理论广泛地应用于不同造山带的研究(Davis et al., 1983; Braathen et al., 1999; Bilotti and Shaw, 2005; Willett et al., 2006; Miyakawa et al., 2010), 揭示出构造楔形体强度与基底滑脱等因素共同控制着褶皱冲断带自相似性生长过程, 决定着楔形体楔顶角与基底倾角共同(线性相关)的变化过程(Davis et al., 1983; Dahlen, 1984)。因此, 根据楔顶角与基底倾角特征(二者之和: 即 β+a)可以将褶皱冲断带大致分为两类: 中–高角度类型(β+a>10°)和低角度类型(β+a<5°), 前者普遍发育较小倾角的前展式断层和较大倾角的反冲断层, 而后者发育倾角大致相似的前展和反冲断层、尤其是反冲断层明显发育(Davis et al., 1983; Bilotti and Shaw, 2005; Buiter, 2012)。同时, 伴随周期性自相似性生长过程, 楔形体常常形成明显的楔顶角度破裂点或突变点“Slope break”, 该突变点常位于以前展式扩展变形特征为主的楔形体前缘(或外带), 和以无序冲断加积变形特征为主的楔形体内带之间的过渡带(Dominguez et al., 2000; Del Castello et al., 2004; Wenk and Huhn, 2013), 与基底属性可能具有一定成因关系(Del Castello et al., 2004; Miyakawa et al., 2010)。值得指出的是, 基于褶皱冲断带实例研究也揭示出, 如: 台湾冲断带、尼日尔三角洲褶皱冲断带等, 地壳浅部(<15~20 km)普遍具有相对均一的物理特性, 控制着楔形体自相似性生长过程; 但是>15~20 km深度的地壳物质具脆–塑性过渡带变形特征, 导致楔形体强度减弱, 楔顶角与基底倾角相关性不明显(Carena et al., 2002; Suppe, 2007)。
2 褶皱冲断带砂箱物理模型主控因素
自然界挤压增生楔基于其变形传播方向通常可以分为两类: 单向汇聚楔形体类(图 2a, Hubbert, 1951)和双向汇聚楔形体类(图 2b, Koons, 1990; Willett et al., 1993), 前者速度不连续点位于活动挡板前缘导致物质难以发生反向位移, 后者速度不连续点位于砂箱模型中部导致砂箱物质能够同时发生向前或向后的位移与变形, 即发生向俯冲盘方向的前展式褶皱冲断变形(“forethrust”)和向活动挡板方向的反向冲断变形(“backthrust”)。
挤压砂箱模型中由于基底变形传播的阶段性和周期性导致其单向汇聚楔形体生长呈阶段性(图 2c, d), 即楔形体前展式扩展变形形成新的前缘冲断层导致楔形体加积增生, 新的楔形体进一步发生缩短(积累应变可能为 10%左右)与增厚变形直到新的前缘断层形成(Mulugeta and Koyi, 1992; Gutscher et al., 1996)。伴随楔形体持续变形增生, 早期逆冲断层倾角逐渐减小(图 2a)。砂箱物理模型和数字模型实验中楔形体加积生长过程服从临界楔理论(图 2d, Mulugeta and Koyi, 1992; Naylor and Sinclair, 2007),且楔形体面积普遍服从线性增长趋势(Koyi, 1995),楔形体可大致分为平顶部分和三角前缘部分, 前者面积具稳定增长特征、后者面积长时间内具有稳定不变的特征(图 2e), 主要归功于楔形体后缘物质的恒定加积作用和前缘物质沿楔形体表面发生扩散。但是, 无论是黏土砂箱模型还是石英砂砂箱模型(图2f), 楔形体内部物质主要发生向上的位移(Cowan and Silling, 1978; Mulugeta and Koyi, 1992)。一般而言, 单向汇聚楔形体可以划分为三个典型的结构和运动学亚带(图2g): 前缘变形带(FDZ)、前缘叠瓦冲断带(FIZ)和内部加积变形带(IAZ)。前缘变形带由新形成的逆冲断层组成, 常形成成对的前展式和反冲断层, 具有较大的水平位移和较小的抬升变形, 因而具垂直拉伸应变椭球变形特征; 前缘叠瓦冲断带常由数条逆冲断层组成, 水平位移较前者小、抬升变形量适中, 因此拉伸应变椭球体较前者小; 内部加积变形带由无序冲断层与前缘叠瓦冲断带分开,水平位移和抬升变形量都极小, 因此通常具有各向同性的变形特征。
俯冲砂箱模型中双向汇聚楔形体也具有数个生长变形周期(Willet et al., 1993; Hoth et al., 2007)。早期快速扩展变形阶段(前楔低位移量冲断、反向楔快速冲断变形), 以形成典型受成对膝折带控制的冲起构造为主(Willet et al., 1993; Hoth et al., 2007), 物质主要发生反向楔内的反向扩展和抬升变形, 随后前楔和反向楔持续发生物质加积变形形成楔形体轴带(图2h)。晚期为低速扩展变形阶段(前楔高位移冲断变形、反向楔低速冲断变形), 以形成持续的冲断岩片或推覆体叠置构造为主(McClay and Whitehouse, 2004; Bigi et al., 2010)。一般而言, 当楔形体高度达到最大时(临界楔形体高度)(图2j), 反向楔载荷过高而难以持续其高滑动变形速率, 此时楔形体轴带相当于活动挡板加速前楔扩展变形(McClay and Whitehouse, 2004; Storti et al., 2000)。前楔与反向楔具有不同的加积增生机制, 前者以前展式和基底加积为主, 反向楔则以前楔物质的向上和反向剪切生长形成为主; 且前楔地貌坡度符合最小临界楔形体理论(图2i), 后者地貌坡度则具有较大争议(Davis et al., 1983; McClay and Whitehouse, 2004)。
2.1 砂箱基底特性因素
砂箱基底特性对砂箱模型模拟过程中楔形体具有不同作用, 其主要因素包括: 基底几何学性质(如:坡度和地貌形态)、有效摩擦角、孔隙流体压力和垂直应力(之比)等。Davis et al. (1983)基于砂箱模型临界楔理论指出砂箱基底坡角变化(增大或减小)会伴随楔顶角变化(减小或增大), 相对于基底砂箱模型中断层仍然具有相似特征, 但相对于水平参考系前展式断层倾角更陡、反向扩展断层更缓。当基底摩擦角和缩短量一定的情况下, 基底倾向后陆的砂箱模型相对于基底倾向前陆(扩展变形方向)的砂箱模型中楔形体较短、较厚(图3a), 主要归因于前者具有较高的平行层缩短和较高的非面积守恒应变特征(Koyi and Vendeville, 2003)。尤其是当基底摩擦系数(或摩擦力)相对较高时, 如: μb=0.55, 基底倾角对砂箱楔形体的影响更加明显, 反之亦然。值得指出的是, 增加基底倾角与增加基底摩擦系数对于楔形体(如: 楔顶高和临界楔顶角)具有相似的作用。Smit et al. (2003)揭示当基底倾角为 0.75°~3.0°之间时,伴随其角度变化石英砂箱模型构造样式具有明显不同特性。低角度砂箱基底倾角形成较宽的、前展式冲断构造变形特征, 倾角较大则具有较窄的、同时具有前展式和反向冲断构造变形特征。当砂箱基底具有不同的正凸起和负地貌形态时(如: 火山口、地堑等), 挤压变形过程会导致砂箱物质发生典型的构造剥蚀(Tectonic erosion)(von Huene and Culotta, 1989; Lallemand et al., 1994)。由于不同的变形机制导致形成复杂的地貌特征(图 3b), 基底正凸起上覆砂箱物质发生反向冲断变形, 楔形体后缘物质常常发生高角度走滑变形和正断层变形(Dominguez et al., 2000)。

(a) 单向汇聚楔形体类型砂箱模型生长过程及其断层演化特征(Marshak and Wilkerson, 1992), 伴随楔形体增高断层倾角逐渐减小; (b) 双向汇聚楔形体类型砂箱模型(McClay and Whitehouse, 2004), 主要由前楔、反向楔和轴带部分组成; (c) 楔形体阶段性扩展变形与生长过程(Mulugeta and Koyi, 1992), 楔形体前缘伴随新生成的逆冲断层前展式生长; (d) 砂箱模型楔形体生长服从临界楔理论 (Mulugeta and Koyi, 1992); (e) 楔形体横截面近似恒定的生长规律 (Koyi, 1995), 楔形体可大致分为面积稳定增长部分和面积快速稳定部分; (f) 黏土和石英砂楔形体内部物质运动轨迹 (Cowan and Silling, 1978; Mulugeta and Koyi, 1992), 揭示砂箱物质普遍具有向上的运动轨迹; (g) 单向汇聚楔形体结构分带性 (Lohrmann et al., 2003), 可大致分为前缘变形带(FDZ)、前缘叠瓦冲断带(FIZ)和内部加积变形带(IAZ); (h) 双向汇聚楔形体类砂箱模型生长变形周期性(Storti et al., 2000), 即早期快速扩展变形阶段(前楔低位移量冲断、反向楔快速冲断变形)和后期低速扩展变形阶段(前楔高位移冲断变形、反向楔低速冲断变形); (i) 前楔和反向楔地表坡度变化特征(Wang and Davis, 1996), 伴随楔形体生长前楔顶角达到最小临界楔角度; (j) 双向汇聚楔形体类砂箱模型生长楔形体高度变化特征(Storti and McClay, 1995), 楔形体高度普遍具有与缩短量之比呈恒定速率的生长过程, 最后达到最大值。图2 砂箱构造物理模型楔形体生长特征图Fig.2 Growth processes of an accretionary wedge in sandbox modeling
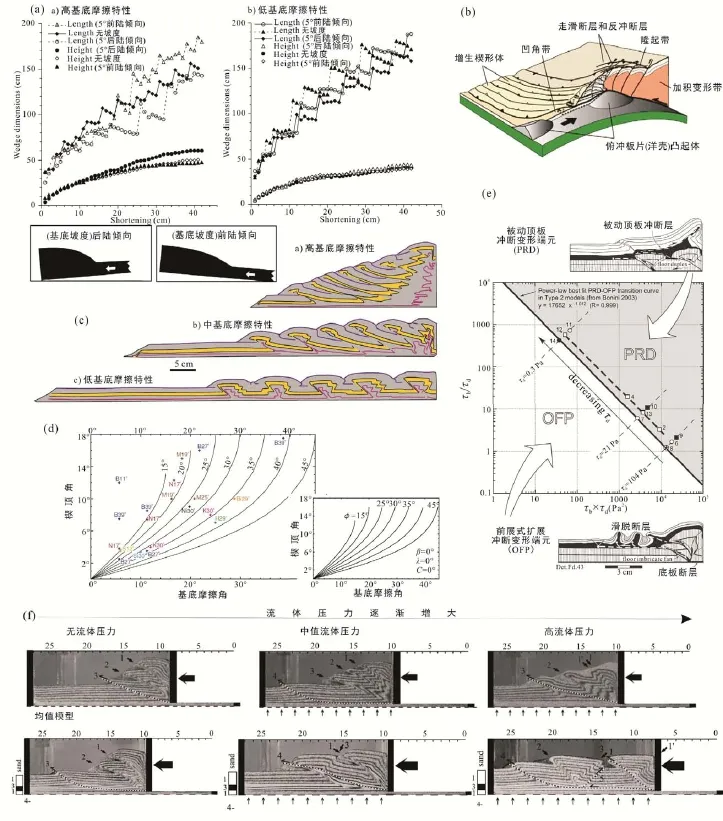
(a) 基底坡度对砂箱模型楔形体特征影响 (Koyi and Vendeville, 2003), 基底倾向后陆的砂箱物理模型相对于基底倾向前陆(扩展变形方向)的砂箱模型中楔形体较短、较厚(尤其是高基底摩擦特性); (b) 基底地貌凸起(如火山口)对楔形体特征影响的三维形态(Dominguez, 2000); (c) 基底差异性摩擦特性对逆冲楔形体形态的影响(Liu et al., 1992), 伴随摩擦系数或强度增大楔顶角明显增大, 且构造运动学也具有明显变化; (d) 水平基底的摩擦系数与楔形体楔顶角或坡度关系符合临界楔理论(Buiter, 2012), 其中小图为大图数字模型结果; (e) 砂箱模型变形样式与基底和砂箱物质内剪切力关系(Bonini, 2007), 揭示基底和砂箱物质内剪切力关系之比控制着楔形体前展式扩展冲断变形或被动顶冲等构造变形过程; (f) 砂箱物质底部流体超压对楔形体的影响(Mourgues and Cobbold, 2006), 流体超压导致楔形体更宽和楔顶角更低。图3 不同基底特性对砂箱构造物理模型楔形体特征的影响作用Fig.3 Influence of basal on the growth and deformation of an accretionary wedge
砂箱模型中基底与砂箱物质的耦合特性(即沿楔形体底部滑脱面)是控制构造楔形体几何和构造特征最重要的参数, 自然界中其主要取决于沉积盖层和流体超压特性。砂箱模型中通过砂箱底部加入不同摩擦系数的物质(如: 玻璃珠μb=0.36、塑料/聚酯薄膜μb=0.21等)决定了砂箱模型中的基底特性。低摩擦系数(或强度)砂箱模型中楔形体变形生长以(可能为对称性)箱状褶皱和冲起结构为主, 具有较大的宽度和较小的楔顶角(图 3c, d), 且前展式冲断和反向冲断都较普遍(Mulugeta, 1988; Liu et al., 1992; 周建勋等, 2002); 而高摩擦系数砂箱模型中楔形体变形生长以叠瓦状冲断构造变形为主, 冲断变形以前展式无序冲断(常具多期活动)为主(Cotton and Koyi, 2000; Koyi et al., 2000; Smit et al., 2003), 且具有较高的平行层缩短变形(Koyi et al., 2004)。高摩擦砂箱基底其主应力轴(σ1)倾向前陆方向, 导致前展式冲断层相对于其反向冲断层具有较低的倾角和更大的缩短变形特征(Davis and Engelder, 1985), 因此Bonini (2003, 2007)认为基底和上覆砂箱物质内剪切力控制着楔形体变形结构特征(图 3e), 尤其是砂箱物质内部滑脱层导致上下变形脱耦、形成典型被动顶冲双重变形结构。砂箱模型中流体超压严重影响楔形体几何形态(图 3f), 挤压增生楔形体具有明显较宽、较薄和较低楔顶角的几何学特征, 伴随挤压过程砂箱底部形成水平滑脱层, 并发生盆地向扩展移动(Cobbold et al., 2001; Mourgues and Cobbold, 2006)。尤其是对于非均质性砂箱物质(即变化的渗透率和内聚力系数特征), 滑脱层沿低渗透层形成、快速盆地向(沿挤压方向)扩展传播, 楔形体常具有较低楔顶角和近似对称的冲起结构特征。
砂箱基底面积(布砂面积, SB)与相关剪切应力大小, 尤其是与侧向固定挡板面积(布砂厚度接触面积, SL)之比值(Souloumiac et al., 2012), 导致楔形体挤压变形过程中, 临近侧向固定挡板处砂箱表面断层发生不同程度弧形弯曲, 从而严重影响砂箱变形 2D剖面重建(Koyi and Cotton, 2004; Schreurs et al., 2006)。当SL/SB<0.1时, 砂箱基底面剪切应力较大、侧向固定挡板与挤压缩短方向相反的剪切应力可以忽略; 当 0.1
2.2 砂箱物质特性因素
砂箱物质特性对于砂箱楔形体变形与演化具有明显的控制作用(魏春光等, 2004; Konstantinovskaya and Malavieille, 2011; Graveleau et al., 2012), 如: 内聚力、摩擦力(或强度)、厚度、孔隙度和渗透率等, 尤其是其垂向属性的变化。一般而言, 砂箱物质强度增加导致其临界楔形体稳定区域面积增大, 既最小临界(楔顶)角变小和最大临(楔顶)界角变大(图 1)。砂箱物质内部软弱层导致楔形体由能干性楔形体的冲断褶皱变形为主构造样式转变为褶皱变形样式为主的特征(图4a)(Yamato et al., 2011)。物质压实作用使其内聚力增强, 从而导致临界(楔顶)角变小形成凸起的地表形体, 但由于内聚力与砂箱物质摩擦强度和流体孔隙压力密切相关, 因此内聚力对整个褶皱冲断带变形影响作用有限(Simpson, 2011)。由于砂箱物质普遍具有瞬时应变增强和应变弱化特性, 使砂箱楔形体具有典型的依赖于物质压实作用的分带性(图4b)。Lohrmann et al. (2003)认为砂箱物质的体积强度受控于其最薄弱层的摩擦强度(如: 断层等),因此早期存在的非均一结构可能使砂箱楔形体局部集中应变从而控制其构造变形过程与样式, 如: 活动断层摩擦特性决定着楔形体不同分段的楔顶角和强度(图 4b)。同时砂箱楔形体向后缘由于断层旋转和弹性物质强度增加导致其体积能干性逐渐增大,不同砂箱物质纵向属性差异导致楔形体后缘集中应变带具有明显的运动学特征差异。尤其是, 砂箱物质侧向非连续性是侧向或斜向断坡、撕裂断裂和转换带等构造形成的重要控制因素(Corrado et al., 1998; Cotton and Koyi, 2000; Marques and Cobbold,2002; Ravaglia et al., 2004), 常常在砂箱物质表面表现为不同逆冲前缘连接带或逆冲岩片侧向终止构造样式, 砂箱物质内部不同岩层厚度空间明显变化。砂箱物质侧向不连续带具有较高的平行层缩短变形和较低逆冲分量(图4f), 逆冲岩片(席)长度与逆冲滑动量可能存在一定的线性关系(Ravaglia et al., 2004)。同时, 流体压力普遍存在降低砂箱物质有效应力的作用, 导致破裂变形作用发生, 因此含水砂箱楔形体具有较低的强度和较高的临界(楔顶)角(Strayer et al., 2001; Cobbold et al., 2001; Mourgues and Cobbold, 2006), 流体压力系数比和楔顶角共同控制着楔形体中滑脱层前展式变形传播和应变集中特征(Pons and Mourgues, 2012)。

(a) 多层滑脱层对楔形体变形影响(Yamato et al., 2011), 单一基底滑脱层导致低速褶皱变形速率和冲断变形构造样式为主, 多层滑脱层导致楔形体变形速率增大和褶皱变形构造样式为主; (b) 不同砂箱物质楔形体特征(Lohrmann et al., 2003), 不同物质楔形体内部加积应变带(IAZ)具有运动学特征差异性, 而其他部分则大致相似; (c) 能干层位置对于砂箱楔形体影响(Teixell and Koyi, 2003), 能干层位于砂箱底部具有相对顶部较高的楔顶角从而控制着楔形体特征; (d) 纯石英砂、石英-重晶石混合砂和石英-云母混合砂三种砂箱物质构造变形过程, 伴随砂箱物质中弹性颗粒物质含量增加, 挤压冲断变形和楔形体几何学变化明显更具均一化特征(Gomes, 2013); (e) 相同挤压条件下水饱和条件下微玻璃珠“GM”、硅粉“SilPwd”、塑料粉末“PVC”、石墨粉“Graph”和前四者混合材料“MatⅣ” 砂箱物质挤压构造变形特征(Graveleau et al., 2011), 硅粉相对于其余几种物质由于具有较高内聚力, 其断层空间距离明显较其他物质窄和密, 前展式和反冲式断层普遍发育; (f) 砂箱物质侧向非连续性转换带在砂箱物质表面表现为不同逆冲前缘连接带或逆冲岩片侧向终止构造样式, 具较高的平行层缩短变形和较低逆冲分量, 逆冲岩片(席)长度与逆冲滑动量可能存在一定的线性关系(Ravaglia et al., 2004)。图4 不同砂箱物质特性对构造楔形体变形的影响作用Fig.4 Influence of material properties on the growth and deformation of an accretionary wedge
除砂箱物质自然属性的差异之外, 不同砂体成型方法(如: 自动化筛砂和倾倒方式等)、上覆地层压力等也可能导致砂箱物质属性体现出一定差异性,从而影响其构造物理模拟结果。自动化筛砂造型形成的砂箱楔形体物质具有较高的砂体密度、分选性、均一性、高压实性和相对较高的应变破裂强度等(Lohrmann et al., 2003; Panien et al., 2006; Gomes, 2013)。磨圆度低、非均质性强、颗粒越粗的砂箱物质, 在挤压变形过程中由于较高的应力分散性常常产生较大的弥散式或分散式变形、较高的应变弱化特征。因此, (新型)砂箱物质材料研究受到越来越多的重视。基于具相似峰值破裂强度等力学特性的石英砂、石英–重晶石混合砂和石英–云母混合砂三种砂箱物质构造模拟揭示, 砂箱物质中塑性颗粒物质(如重晶石、云母等矿物)含量增加将形成更加均一的挤压冲断变形和楔形体几何学(图 4d), 同时也导致混合石英砂类砂箱物质需要较高的剪切应变量才能达到与纯石英砂相似的挤压破裂变形(Gomes, 2013)。水饱和条件下微玻璃珠、硅粉、塑料粉末、石墨粉和前四者混合材料砂箱实验表明(Graveleau et al., 2011), 相同挤压条件下微玻璃珠和塑料粉末砂箱物质产生相对较少的前展式断层和较低的楔顶角, 挤压缩短变形过程中微玻璃珠楔形体前缘产生明显的褶皱缩短变形, 而后者前缘则以脆性破裂变形为主; 硅粉则具有更多的脆性破裂变形行为特征,前展式和反冲式断层普遍发育, 且具较大的楔顶角,同时由于硅粉具有较高内聚力, 其断层空间距离明显较其他物质窄和密(图4e)。
基于物质能干性和非能干性岩层实验表明, 能干性岩层(如: 石英砂)缩短变形以冲断构造变形为主, 非能干性岩层(如: 玻璃珠)以褶皱变形为主, 但不同的基底摩擦属性会导致典型的集中应变发生(尤其是低摩擦特性的砂箱基底)。能干性岩层会导致砂箱楔形体楔顶角明显增大, 且能干性岩层位于砂箱底部相对于顶部对楔顶角增大作用更加明显(图4c)。砂箱内部软弱层或滑脱层除要相对于砂箱基底和其周围砂箱物质具有更低的能干性外(Kukowski et al., 2002), 其厚度和几何学展布对于楔形体变形也具有重要的影响作用, 主要归功于其低应力–应变条件有助于变形的扩展传播。滑脱层深度控制着楔形体褶皱变形空间格架及其构造样式, 较浅的滑脱层导致楔形体具有更普遍的、更宽向背斜和深部冲断变形特征, 而较深的滑脱层导致楔形体具有更快的传播变形特征和褶皱冲断变形样式(Rossi and Storti, 2003; Yamato et al., 2011), 尤其是叠瓦冲断构造样式。滑脱层侧向非均质性导致形成不同波长的冲断层系、弧形构造等, 而其垂向非均质性决定着砂箱模型中不同级别的构造样式, 即底部滑脱层系为一级结构、中部滑脱层系为二级结构。值得指出的是, 区别于挤压砂箱物理模型和数字模型中滑脱层对构造变形过程的强烈控制作用(Kukowski et al., 2002; Stockmal et al., 2007; Konstantinovskaya and Malavieille, 2011; 沈礼等, 2012), 其在俯冲挤压砂箱模型中滑脱层对于砂箱楔形体变形作用明显较弱(Hoth et al., 2007)。
2.3 砂箱动力学特性因素
砂箱动力学特性对砂箱模型模拟过程中楔形体差异性作用主要体现在: 砂箱不同几何边界(如: 活动或固定挡板)、不同挤压汇聚方向(即缩短方向与挡板边界, McCaffrey, 1992)和差异挤压汇聚速率导致砂箱物质变形过程存在典型的非均一性属性。斜向汇聚碰撞导致砂箱楔形体存在较大楔顶角和典型分带性(Biagi, 1988; Martinez et al., 2002; McClay et al., 2004), 楔形体外带逆冲断层倾向砂箱挡板、地表破裂普遍平行逆断层具有一定的斜度; 内带与外带之间由向外带增厚的、由少量逆断层形成的新月形构造带分割, 内带具有典型扭压走滑特征、且切割早期逆断层及其分支(图5a)。值得指出的是, 斜向汇聚砂箱变形中楔形体变形过程普遍具有分散式应变阶段、斜向应变阶段和应变集中三个不同阶段(图5b)(Leever et al., 2011)。当楔形体后缘阻挡体较薄时,变形带相对较宽且内部扭压走滑带普遍位于砂箱模型速度不连续点; 当活动挡板较厚时, 内部扭压走滑带具有前陆向迁移特征。伴随斜向碰撞夹角逐渐增大(φ>45°~55°, 砂箱物质位移矢量与砂箱边界活动挡板或速度不联系点的夹角), 内带逆冲断层倾角明显变陡、数量减少, 且断层逐渐垂直、汇聚形成主断层; 尤其是少量走滑断层会体现出正断层特征(图5c)。在基底内摩擦角较大的砂箱模型中, 走滑断层主要出现在具有较高斜向夹角的碰撞挤压模型中(90°>φ>40°~45°), 而在较低斜向夹角的碰撞挤压模型中位移的走滑分量主要被逆断层所吸收, 因此应变集中主要发生于较高斜向夹角碰撞过程中(图5d);如果砂箱模型基底具有更低的摩擦特征, 其临界斜向夹角变大(μb=0.2时, φ=~60°)(Martinez et al., 2002);尤其是, 较高的斜向夹角碰撞挤压可能会形成几何学近似对称的、具有较高凸起轴带(被走滑断层切割)的双向汇聚楔形体(McClay et al., 2004; Leever et al., 2011)。

(a) 三维斜向碰撞挤压砂箱模型分带性(Biagi, 1988); (b) 斜向汇聚挤压(φ=30°)砂箱模型楔形体演化三阶段性(Leever et al., 2011), 即分散式应变阶段、斜向应变阶段和应变集中阶段; (c) 高斜向挤压碰撞夹角砂箱模型走滑断层特征(Malavieille et al., 1992), 其中少量走滑断层体现出正断层特征; (d) 斜向汇聚挤压夹角属性对楔形体变形影响(McClay et al., 2004), 低斜向夹角变形缺少走滑断层, 走滑断层构造变形发生临界夹角为40°~45°; (e) 砂箱模型走向挤压速率变化与不同弧形楔形体关系(Reiter et al., 2011), 楔形体前缘冲断变形具有典型弧形几何学特征且其弧度伴随速率走向对比性增大而增大; (f) 双层和多层摩擦-粘性层耦合特性对楔形体的影响(Smit et al., 2003; Couzens-Schultz et al., 2003; Graveleau et al., 2012), 低挤压缩短速率楔形体中滑脱层有效变形使楔形体前展式和反向式冲断多期次活动。图5 不同砂箱动力学特性对构造楔形体的作用Fig.5 Influence of dynamics on the growth and deformation of an accretionary wedge
砂箱模型不同几何边界导致砂箱物质具有明显不同的切线运动速率, 从而形成不同几何学和运动学特征(Bonini et al., 1999; Macedo and Marshak , 1999; Marques and Cobbold, 2002), 如: 弧形构造可能受控于初始地貌的几何学差异和/或活动挡板的几何学差异。尤其是活动挡板前缘倾角面不同于砂箱物质内摩擦角时(~30°)时, 砂箱物质通过活动挡板与活动的反向剪切带之间物质加积和压缩机制(沿前缘倾角面传播)形成砂箱模型的“有效挤压体”(Effective indenter), 从而控制砂箱模型楔形体形成演化(Bonini et al., 1999; Persson, 2001)。因此, 活动挡板前缘倾角面存在两种不同端元模型, 倾角面<45°时形成楔形体剪切传播点和活动挡板前缘点一致; 倾角面>60°时楔形体剪切传播点和活动挡板前缘点不一致。
Reiter et al. (2011)基于砂箱模型中走向缩短速率的变化揭示出斜向物质传播、冲断变形和物质旋转相关的系列弧形构造。走向缩短速率变化较小时,楔形体走向具有连续性、且具20°~60°弧形结构; 走向速率变化较大时, 由于较高角度弧形结构(大于60°)使楔形体走向不具有连续性(图5e)。具有较快挤压缩短速率楔形体前缘冲断变形结构发生侧向传播(向低速楔形体前缘), 从而影响后者前缘冲断变形和楔形体几何学特征。由于不同于砂箱物质中石英砂低(或非)应变敏锐性, 粘性材料或粘弹性材料具有一定的应变相关性(Weijermars and Schmeling, 1986; Davis et al., 1983), 因此挤压砂箱模型中不同走向缩短速率对楔形体变形至关重要, 如: 挤压缩短速率控制着单向和双向挤压楔形体地表形态和楔体大小(Rossetti et al., 2000)。较快缩短速率使楔形体具有更窄、更厚的几何特征, 更易于发生应变集中化和前展式冲断变形、较陡的前缘楔顶角, 楔形体体现出较高摩擦属性; 低缩短速率使楔形体较宽、厚度较薄, 具有分散式变形与应变特征, 以双向汇聚的褶皱变形为主(Smit et al., 2003; Pichot and Nalpas, 2009)。受控于机制层厚度和缩短速率(Nalpas and Brun, 1993), 低挤压速率下滑脱层有效变形使楔形体前展式和反向式冲断多期次活动; 而高挤压速率下滑脱层重要性相对较弱、楔形体常具前展式扩展变形序列(图5f)(Smit et al., 2003; Couzens-Schultz et al., 2003; Yamato et al., 2011)。
2.4 砂箱浅表作用过程因素
浅表作用过程(如: 剥蚀与沉积)直接影响砂箱物质模型地貌, 同时与楔形体内部变形具有典型互馈过程(Koons, 1990; Beaumont et al., 1992; Willett, 1999; Hilley and Strecker, 2004)。浅表作用过程首先影响浅部物质负载, 从而增加或减小砂箱基底摩擦应力, 同时也导致楔形体体积强度增加或减小; 其次剥蚀和沉积作用都可能导致楔顶角减小、楔形体处于不稳定状态(即亚稳定状态), 从而导致楔形体通过变形调整达到临界稳态平衡状态。不同于沉降过程的连续性, 自然界中剥蚀过程常常具有非连续性和阶段性, 因此砂箱模型实验中的浅表作用过程普遍被简化, 如: 倾斜的或水平的剥蚀界面(Persson and Sokoutis, 2002; Konstantinovskaia and Malavieille, 2005), 与海拔线性相关的剥蚀速率(Hoth et al., 2006)或非线性河流剥蚀规律(Cruz et al., 2010)等。
浅表剥蚀作用过程普遍导致楔形体扩展变形速率减小、宽度减小、断层倾角变陡、活动时间增长(多期活动与无序冲断)和应变集中化(剥蚀区域)等(图6a), 尤其是走向剥蚀速率的变化可能导致形成弧形褶皱冲断带(Marques and Cobbold, 2002); 浅表沉积作用具有与之相反的特性(Storti and McClay, 1995; Willett, 1999; Hoth et al., 2006; Konstantinovskaia and Malavieille, 2005, 2011; Bigi et al., 2010; Cruz et al., 2010)。砂箱楔形体演化不仅对剥蚀和沉积等浅表作用具有敏锐的响应性, 且对剥蚀和沉积等浅表作用所发生的区域也具有响应性。当剥蚀发生在双向楔形体前楔时能够导致冲断层数量减少、倾角增大, 断层活动却并不具有无序冲断活动特征; 当剥蚀发生在反向楔(或同时发生在前楔与反向楔)时对冲断层数量并没有明显影响, 但断层活动却具有无序冲断活动特征(Hoth et al., 2006, 2007)。非均一性浅表剥蚀作用导致砂箱逆冲断层多期活动使楔形体变形与应变集中化, 最终导致楔形体发生反向位移(图6b)(Persson et al., 2004; Cruz et al., 2008); 楔形体轴带(地貌界限)受局部剥蚀作用也发生明显的迁移, 前楔剥蚀导致轴带后楔向迁移、后楔剥蚀导致轴带前楔向迁移(图 6c)(Willett, 1999; Cruz et al., 2008)。

(a) 浅表剥蚀和沉积作用对楔形体的影响(Storti and McClay, 1995; Cruz et al., 2010); (b) 浅表剥蚀作用对楔形体断层特征影响 (Persson et al., 2004); (c) 局部剥蚀作用导致楔形体地貌迁移(Cruz et al., 2008), 楔形体地貌分隔带(地貌界限)向局部剥蚀反向位移; (d) 不同砂箱基底摩擦属性、剥蚀强度对砂箱剥蚀特征的影响(Malavieille, 2010), 低摩擦强度基底砂箱模型剥蚀作用发生在楔形体中部高陡冲断带; (e) 浅表剥蚀作用对多套滑脱层系砂箱模型楔形体构造变形的影响(Konstantinovskaia and Malavieille, 2011); (f)同构造沉积与剥蚀浅表作用对楔形体构造变形特征的作用(McClay and Whitehouse, 2004); (g) 受控于同沉积作用的楔形体前缘构造变形三端元模式(Duerto and McClay, 2009), 出露型褶皱冲断带样式、距离隐伏冲断结构样式和短距离隐伏冲断结构样式。图6 浅表作用过程对砂箱构造楔形体的作用Fig.6 Influence of surface processes on the growth and deformation of an accretionary wedge
砂箱物质剥蚀路径主要依赖于其初始结构位置和浅表作用强度, 较高的剥蚀作用显著增加砂箱物质剥蚀路径倾角, 从而使楔形体深部物质剥蚀出露;倾角较缓的活动挡板更有利于其前缘物质具有更陡的剥蚀路径(Cruz et al., 2008; Konstantinovskaia and Malavieille, 2005, 2011)。受控于砂箱基底摩擦特性及其相关的断层传播变形过程, 低摩擦强度基底(即具基底滑脱属性)砂箱模型剥蚀作用相对于高摩擦强度基底的砂箱模型较弱, 主要发生在楔形体中部产状高陡的冲断带(即前缘叠瓦冲断带后缘和内部加积变形带前缘); 高摩擦强度基底的砂箱模型剥蚀作用主要发生于中等倾角的冲断带(即前缘叠瓦冲断带)(图 6d), 尤其是剥蚀强度的增大会导致楔形体最大剥蚀带向楔形体内部迁移(Malavieille, 2010; Konstantinovskaia and Malavieille, 2005, 2011)。砂箱模型具多层滑脱层层系时, 上述剥蚀作用和现象会得到不同程度放大, 导致砂箱物质基底层俯冲冲断变形形成典型的伴随剥蚀速率变化而变化的多重构造、飞来峰构造等, 但却不利于反向冲断层发育(图6e)。不同于较小剥蚀斜坡角条件下(4°~6°)楔形体形成的复背斜双重构造, 当剥蚀斜坡角为8°时(临界斜坡角), 滑脱层上部楔形体形成断坡背斜、下部形成具正滑特征双重构造和底板俯冲构造。
与浅表剥蚀作用相似, 浅表沉积作用也会改变楔形体其前缘(即前陆盆地)物质强度、重力及应力状态, 导致楔形体楔顶角降低、冲断层数量减少(图6a)和逆冲断层活动序列改变。单向挤压楔形体因此普遍发生冲断层的多期无序构造活动以及后缘方向冲断, 从而更加有利于砂箱楔形体趋于临界稳态平衡状态(Storti and McClay, 1995; Persson and Sokoutis, 2002)。双向挤压楔形体中当沉积作用发生于楔形体一侧时(前楔或者反向楔)导致楔形体变形分异, 前楔发生沉积作用导致前展式冲断层数量减少且构造变形无序化和反向楔变形活动及其楔顶角强烈减小(McClay and Whitehouse, 2004; Bigi et al., 2010)。尤其是当同构造沉积和剥蚀浅表作用共同发生时, 楔形体反向冲断构造变形加剧(图6f)。
前陆盆地沉积物质特性(均一性或变化的同构造沉积)对冲断楔形体构造特征具有重要的控制作用, 普遍阻止楔形体前缘新逆冲断层发育、增加楔形体下部基底俯冲冲断活动等(Duerto and McClay, 2009; Bigi et al., 2010), 因此存在三种端元模型(图6g): 缺失同构造沉积的出露型褶皱冲断带样式、中等同构造沉积(速率)的长位移距离隐伏冲断结构样式(即欠充填盆地)和高同构造沉积(速率)的短距离隐伏冲断结构样式。不同构造端元主要受控于同构造沉积厚度与构造变形前地层厚度之比, 由挤压楔形体前缘垂直和水平应力平衡状态决定着其临界比率为1/3(Duerto and McClay, 2009)。此外, 冲断楔形体前缘褶皱变形几何学生长过程主要受控于其沉积速率和抬升速率的相互关系, 伴随沉积速率的增大褶皱变形难度增大(Nalpas et al., 2003; Pichot and Nalpas, 2009), 尤其是断层相关褶皱两侧具有非均一性沉积速率时导致非对称性变形特征, 即变形向低沉积速率侧聚集。
3 讨论与结论
地壳浅部褶皱冲断带普遍受控于具耦合互馈特性的多种机制或边界条件, 从而具有长期的构造演化过程和复杂的构造特征, 其不同控制因素, 如:结构几何特性、基底特性、物质(非均一性)特性、动力学特性和浅表作用过程等, 由于复杂的耦合互馈性难以有效量化评估, 同时也限制着我们对于褶皱冲断带构造体系的四维时空结构演化的理解。砂箱物理模型方法学的兴起与发展, 为我们解译褶皱冲断带的演化过程及其动力学机制提供了独立有效的手段。构造砂箱物理模型已揭示褶皱冲断带体系构造变形普遍具符合库伦临界楔理论的自相似性生长过程, 其多种机制或边界条件对于褶皱冲断带构造体系具重要控制作用, 这些典型机制包括: 基底特性(基底几何学、有效摩擦角、基底耦合性和流体超压)、变形物质特性(空间几何学、能干层、流变学和非均一性)、动力学机制(砂箱几何边界、汇聚速率和汇聚方向)、浅表作用(剥蚀和沉降)等。
构造砂箱模型对于浅表褶皱冲断带构造体系解译具有独特优势的同时, 它也具有与生俱来的缺点。砂箱物质和地壳浅部地层物质具有相似的流变学特征, 但其变形边界条件仅代表自然变形系统中的简化条件。因此, 砂箱模型的可重复性虽然总体规律可能一致, 但完全一致的可重复性实验模拟是难以控制的。但这并不意味着构造砂箱物理模型的不可靠性和科学性, 我们仍必须了解构造模拟过程中人为因素的影响也可能导致实验模拟结果的重要变化。
基于本文有限长度很难系统全面地综述褶皱冲断带构造砂箱物理模型的研究结果和进展, 尤其是构造砂箱物理模型的研究已长达两个多世纪。伴随砂箱物理模型在构造变形过程及其动力学机制研究中的广泛使用, 其挑战性在于如何把创新性砂箱装置、新型砂箱物质、全时三维监测和三维应变量化手段等融入不同的砂箱模型中, 有效解译地壳浅部褶皱冲断带变形的实际问题。尽管大量砂箱模型研究已经揭示出对于构造变形过程广泛的不同因素具有明显不同的控制和影响作用, 但是目前也仍有许多变形细节及其相关因素未做深入的模型研究, 如:温度相关的属性、重力均衡机制、流体压力、应力与应变集中等; 此外, 典型互馈机制的浅表构造、剥蚀和沉降等在砂箱构造物理模型中的研究越来越受到重视、但也有待更深入研究, 如: 剥蚀与沉降的时间和方式模型、物质运输等。在砂箱模型设备装置上, 虽然基于 X射线成像技术的全时三维监测手段和基于光应变监测元件的三维应变量化手段等, 对于揭示砂箱模型连续内部变形过程具有独特性, 但它不仅依赖于砂箱厚度和宽度, 还依赖于砂箱物质, 如: 石英砂相对于黏土物质具有明显较好的可视性。值得指出的是, 构造砂箱物理模型 200年以来的持续进步和发展, 不仅不断扩展了构造地质学研究领域, 同时也不断增进了我们对于构造地质学的新发现。
致谢: 感谢审稿专家对文章提出宝贵的修改意见。
沈礼, 贾东, 尹宏伟, 孙闯, 张勇, 范小根. 2012. 基于粒子成像测速(PIV)技术的褶皱冲断构造物理模拟. 地质论评, 58(3): 471–480.
魏春光, 周建勋, 何雨丹. 2004. 岩石强度对冲断层形成特征影响的砂箱实验研究. 地学前缘, 11(4): 559–565.
周建勋, 魏春光, 朱战军. 2002. 基底收缩对挤压构造变形特征影响——来自砂箱实验的启示. 地学前缘, 9(4): 377–382.
Beaumont C, Fullsack P and Hamilton J. 1992. Erosional control of active compressional orogens // McClay K R. Thrust Tectonics. London: Chapman & Hall: 1–18.
Biagi R. 1988. Géométrie et cinématique des prismes d'accrétion sédimentaire: modélisation analogique. Montpellier: Université de Montpellier II: 1–76.
Bigi S, Di Paolo L, Vadacca L and Gambardella G. 2010. Load and unload as interference factors on cyclical behavior and kinematics of Coulomb wedges: Insights from sandbox experiments. Journal of Structural Geology, 32(2): 28–44.
Bilotti F and Show J H. 2005. Deep-water Niger Delta fold and thrust belt modeled as a critical-taper wedge: The influence of elevated basal fluid pressure on structural styles. AAPG Bulletin, 89: 1475–1491.
Bonini M. 2003. Detachment folding, fold amplification, and diapirism in thrust wedge experiments. Tectonics, 22(6): 1065.
Bonini M, Sokoutis D, Talbot C J, Boccaletti M and Milnes A G. 1999. Indenter growth in analogue models of Alpine-type deformation. Tectonics, 18(1): 119–128.
Bonini M. 2007. Deformation patterns and structural vergence in brittle-ductile thrust wedges: An additional analogue modelling perspective. Journal of Structural Geology, 29: 141–158.
Bonnet C, Malavieille J and Mosar J. 2007. Interactions between tectonics, erosion, and sedimentation during the recent evolution of the Alpine orogen: Analogue modeling insights. Tectonics, 26, doi: 10.1029/ 2006TC002048.
Braathen A, Bergh S G Jr and Maher H D. 1999. Application of a critical wedge taper model to the Tertiary transpressional fold-thrust belt on Spitsbergen, Svalbard. GSA Bulletin, 111(8): 1–19.
Buiter S H. 2012. A review of brittle compressional wedge models. Tectonophysics, 530-531: 1–17.
Cadell H M. 1888. Experimental researches in mountain building. Transactions of the Royal Society of Edinburgh, 35: 337–357.
Carena S, Suppe J and Kao H. 2002. Active detachment of Taiwan illuminated by small earthquakes and its control of first-order topography. Geology, 30(10): 935–938.
Cobbold P R, Durand S and Mourgues R. 2001. Sandbox modelling of thrust wedges with fluid-assisted detachments. Tectonophysics, 334(3–4): 245–258.
Corrado S, Di Bucci D, Naso G and Faccenna C. 1998. Influence of palaeogeography on thrust system geometries: An analogue modeling approach for the Abruzzi-Molise (Italy) case history. Tectonophysics,296: 437–453.
Cotton J and Koyi H. 2000. Modeling of thrust fronts above ductile and frictional detachments: Application to structures in the Salt Range and Potwar Plateau, Pakistan. Geological Society of America Bulletin, 112 (3): 351–363.
Couzens-Schultz B A, Vendeville B C and Wiltschko D V. 2003. Duplex style and triangle zone formation: Insights from physical modeling. Journal of Structural Geology, 25(10): 1623–1644.
Cowan D S and Silling R M. 1978. A dynamic scaled model of accretion at trenches and its implications for the tectonic evolution of subduction complexes. Journal of Geophysical Research, 83: 5389–5396.
Cruz L, Teyssier C, Perg L, Take A and Fayon A. 2008. Deformation, exhumation, and topography of experimental doubly-vergent orogenic wedges subjected to asymmetric erosion. Journal of Structural Geology, 30(1): 98–115.
Cruz L, Malinski J, Wilson A, Take W A and Hilley G. 2010. Erosional control of the kinematics and geometry of fold-and-thrust belts imaged in a physical and numerical sandbox. Journal of Geophysical Research: Solid Earth, 115, B09404, doi: 10.1029/2010JB007472. Dahlen F A. 1984. Non cohesive critical coulomb wedges: An exact solution. Journal of Geophysical Research: Solid Earth, 89(B12): 10125–10133. DOI: 10.1029/ JB089iB12p10125.
Dahlen F A. 1990. Critical taper model of fold-and-thrust belts and accretionary wedges. Annual Review of Earth and Planetary Sciences, 18: 55–99.
Davis D, Suppe J and Dahlen F A. 1983. Mechanics of fold-and-thrust belts and accretionary wedges. Journal of Geophysical Research: Solid Earth, 88(B12): 1153–1172. DOI: 10.1029/JB088iB02p01153
Davis D M and Engelder T. 1985. The role of salt in fold-and-thrust belts. Tectonophysics, 119(1-4): 67–88.
Del Castello M, Pini G A and McClay K R. 2004. Effect of unbalanced topography and overloading on Coulomb wedge kinematics: Insights from sandbox modeling. Journal of Geophysical Research: Solid Earth, 109(B5): B05405.
Dominguez S, Malavieille J and Lallemand S E. 2000. Deformation of accretionary wedges in response to seamount subduction: Insights from sandbox experiments. Tectonics, 19(1): 182–196.
Duerto L and McClay K R. 2009. The role of syntectonic sedimentation in the evolution of doubly vergent thrust wedges and foreland folds. Marine and Petroleum Geology, 26(7): 1051–1069.
Flint J J. 1973. Experimental development of headward growth of channel networks. Geological Society of America Bulletin, 84(3): 1087–1094.
Gomes C J S. 2013. Investigating new materials in the context of analog-physical models. Journal of Structural Geology, 46: 158–166.
Graveleau F, Hurtrez J E, Dominguez S and Malavieille J. 2011. A new experimental material for modeling relief dynamics and interactions between tectonics and surface processes. Tectonophysics, 513: 68–87.
Graveleau F, Malavieille J and Dominguez S. 2012. Experimental modelling of orogenic wedges: A review. Tectonophysics, 538-540: 1–66.
Gutscher M A, Kukowski N, Malavieille J and Lallemand S. 1996. Cyclical behavior of thrust wedges: Insights from high basal friction sandbox experiments. Geology, 24(2): 135–138.
Hall J. 1815. On the vertical position and convolutions of certain strata and their relation with granite. Transactions of the Royal Society of Edinburgh, 7: 79–108.
Hilley G E, Strecker M R and Ramos V A. 2004. Growth and erosion of fold-and-thrust belts, with an application to the Aconcagua fold-and-thrust Belt, Argentina. Journal of Geophysical Research, 109: B01410. doi: 10.1029/ 2002JB002282.
Hoth S, Adam J, Kukowski N and Oncken O. 2006. Influence of erosion on the kinematics of bivergent orgens: Results from scaled sandbox simulations // Willett S D, Hovius N, Brandon M T and Fisher D M. Tectonics, Climate, and Landscape Evolution. The Geological Society of America, Special Paper, 398: 201–225.
Hoth S, Hoffmann-Rothe A and Kukowski N. 2007. Frontal accretion: an internal clock for bivergent wedge deformation and surface uplift. Journal of Geophysical Research, 112, doi: 10.1029/2006JB004357.
Hubbert M K. 1951. Mechanical basis for certain familiar geologic structures. Bulletin of the Geological Society of America, 62: 355–372.
Konstantinovskaia E and Malavieille J. 2005. Erosion and exhumation in accretionary orogens: Experimental and geological approaches. Geochemistry, Geophysics,Geosystems, 6: Q02006.
Konstantinovskaya E and Malavieille J. 2011. Thrust wedges with décollement levels and syntectonic erosion: A view from analog models. Tectonophysics, 502: 336–350.
Koons P O. 1990. Two sided orogen: Collision and erosion from the sandbox to the Southern Alps, New Zealand. Geology, 18(8): 679–682.
Koyi H. 1995. Mode of internal deformation in sand wedges. Journal of Structural Geology, 17(2): 293–300.
Koyi H A, Hessami K and Teixell A. 2000. Epicenter distribution and magnitude of earth quakes in foldthrust belts: Insights from sandbox models. Geophysical Research Letters, 27(2): 273–276.
Koyi H A and Vendeville B C. 2003. The effect of décollement dip on geometry and kinematics of model accretionay wedges. Journal of Structural Geology, 25(9): 1445–1450.
Koyi H A, Sans M, Teixell A , Cotton J and Zeyen H. 2004. The significance of penetrative strain in the restoration of shortened layers-insights from sand models and the Spanish Pyrenees // McClay K R. Thrust Tectonics and Hydrocarbon Systems. American Association of Petroleum Geologists Memoir, 82: 207–222.
Koyi H A and Cotton J. 2004. Experimental insights on the geometry and kinematics of fold-and-thrust belts above weak, viscous evaporitic décollement: A discussion. Journal of Structural Geology, 26: 2139-2143.
Kukowski N, Lallemand S E, Malavieille J, Gutscher M A and Reston T J. 2002. Mechanical decoupling and basal duplex formation observed in sandbox experiments with application to the western Mediterranean Ridge accretionary complex. Marine Geology, 186(1-2): 29–42.
Lallemand S E, Schnurle P and Malavieille J. 1994. Coulomb theory applied to accretionary and nonaccretionary wedges-possible causes for tectonic erosion and/or frontal accretion. Journal of Geophysical Research: Solid Earth, 99(B6): 12033–12055.
Leever K A, Gabrielsen R H, Sokoutis D and Willingshofer E. 2011. The effect of convergence angle on the kinematic evolution of strain partitioning in transpressional brittle wedges: Insight from analog modeling and high-resolution digital image analysis. Tectonics, 30, doi: 10.1029/2010TC002823.
Liu H, McClay K R and Powell D. 1992. Physicalmodels of thrust wedges // McClay K R. Thrust Tectonics. London: Chapman and Hall: 71–81.
Lohrmann J, Kukowski N, Adam J and Oncken O. 2003. The impact of analogue material properties on the geometry, kinematics, and dynamics of convergent sand wedges. Journal of Structural Geology, 25(10): 1691–1711.
Martinez A, Malavieille J, Lallemand S and Collot J Y. 2002. Partition de la deformation dans un prisme d'accrétion sédimentaire en convergence oblique: Approche expérimentale. Bulletin de la Societe Geologique de France, 173(1): 17–24.
Macedo J and Marshak S. 1999. Controls on the geometry of fold-thrust belt salients. Geological Society of America Bulletin, 111(12): 1808–1822.
Malavieille J. 2010. Impact of erosion, sedimentation, and structural heritage on the structure and kinematics of orogenic wedges: Analog models and case studies. GSA Today, 20(1): 4–10.
Malavieille J, Calassou S, Lallemand S and Larroque C. 1992. Modélisation analogique des prismes d'accrétion océanique. France: Produit et réalisé par SNEA(P): 1–28.
Marques F O and Cobbold P R. 2002. Topography as a major factor in the development of arcuate thrust belts insights from sandbox experiments. Tectonophysics, 348(4): 247–268.
Marshak S and Wilkerson M S. 1992. Effect of overburden thickness on thrust-belt geometry and development. Tectonics, 11(3): 560–566.
McCaffrey R. 1992. Oblique plate convergence, slip vectors, and forearc deformation. Journal of Geophysical Research: Solid Earth, 97(B6): 8905–8915.
McClay K R and Whitehouse P S. 2004. Analog modeling of doubly vergent thrust wedges // McClay C R. Thrust tectonics and hydrocarbon systems. AAPG Memoir, 82: 184–206.
McClay K R, Whitehouse P S, Dooley T and Richards M. 2004. 3D evolution of fold and thrust belts formed by oblique convergence. Marine and Petroleum Geology, 21(7): 857–877.
McClay K R, Shaw J and Suppe J. 2011. Thrust fault-related folding. AAPG Memoir, 94: 1–392.
Miyakawa A, Yamada Y and Matsuoka T. 2010. Effect of increased shear stress along a plate boundary fault on the formation of an out-of-sequence thrust and a break in surface slope within an accretionary wedge, based onnumerical simulations. Tectonophysics, 484: 127–138.
Morgan J K and McGovern P J. 2005. Discrete element simulations of gravitational volcanic deformation: 2. Mechanical analysis. Journal of Geophysical Research: Solid Earth, 110, doi: 10.1029/2004JB003253.
Mourgues R and Cobbold P R. 2006. Thrust wedges and fluid overpressures: Sandbox models involving pore fluids. Journal of Geophysical Research: Solid Earth, 111, B05404, doi: 10.1029/2004JB003441
Mourgues R, Lacoste A and Garibaldi C. 2013. The Coulomb critical taper theory applied to gravitational instabilities. Journal of Geophysical Research: Solid Earth, 119, doi: 10.1002/2013JB010359.
Mulugeta G. 1988. Squeeze-box in a centrifuge. Tectonophysics, 148(3–4): 323–335.
Mulugeta G and Koyi H. 1992. Episodic accretion and strain partitioning in a model sand wedge. Tectonophysics, 202(2–4): 319–333.
Nalpas T and Brun J P. 1993. Salt flow and diapirism related to extension at crustal scale. Tectonophysics, 228(3-4): 349–362.
Nalpas T, Gapais D, Vergès J, Barrier L, Gestain V, Leroux G, Rouby R and Kermarrec J J. 2003. Effects of rate and nature of synkinematic sedimentation on the growth of compressive structures constrained by analogue models and field examples // McCann T and Saintot A. Tracing Tectonic Deformation Using the Sedimentary Record. Geological Society, London, Special Publications, 208: 307–319.
Naylor M and Sinclair H D. 2007. Punctuated thrust deformation in the context of doubly-vergent thrust wedges: Implications for the localization of uplift and exhumation. Geology, 35(6): 559–562.
Panien N, Schreurs G and Pfiffner A. 2006. Mechanical behaviour of granular materials used in analogue modelling: Insights from grain characterisation, ringshear tests and analogue experiments. Journal of Structural Geology, 28: 1710–1724.
Paola C, Staub K, Mohrig D and Reinhardt L. 2009. The “unreasonable effectiveness” of stratigraphic and geomorphic experiments. Earth-Science Reviews, 7: 1–43.
Persson K S. 2001. Effective indenters and the development of double-vergent orogens: Insights from analogue sand models // Koyi H A and Mancktelow N S. Tectonic Modeling: A Volume in Honor of Hans Ramberg. Geological Society of America Memoirs, 193: 191–206.
Persson K S and Sokoutis D. 2002. Analogue models of orogenic wedges controlled by erosion. Tectonophysics, 356(4): 323–336.
Persson K S, Garcia-Castellanos D and Sokoutis D. 2004. River transport effects on compressional belts: First results from an integrated analogue-numerical model. Journal of Geophysical Research: Solid Earth, 109: B01409. doi: 10.1029/2002JB002274.
Pichot T and Nalpas T. 2009. Influence of synkinematic sedimentation in a thrust system with two decollement levels: Analogue modelling. Tectonophysics, 473(3–4): 466–475.
Pons A and Mourgues R. 2012. Deformation and stability of over-pressured wedges: Insight from sandbox models. Journal of Geophysical Research: Solid Earth, 117: B09404. doi: 10.1029/2012JB009379.
Ravaglia A, Turrini C and Seno S. 2004. Mechanical stratigraphy as a factor controlling the development of a sandbox transfer zone: A three-dimensional analysis. Journal of Structural Geology, 26: 2269–2283.
Reiter K, Kukowski N and Ratschbacher L. 2011. The interaction of two indenters in analogue experiments and implications for curved fold-and-thrust belts. Earth and Planetary Science Letters, 302: 132–146.
Rossetti F, Faccenna C, Ranalli G and Storti F. 2000. Convergence rate-dependent growth of experimental viscous orogenic wedges. Earth and Planetary Science Letters, 178(3–4): 367–372.
Rossi D and Storti F. 2003. New artificial granular materials for analogue laboratory experiments: Aluminium and siliceous microspheres. Journal of Structural Geology, 25: 1893–1899.
Schreurs G, Buiter S H, Boutelier D, Corti G, Costa E, Cruden A, Daniel J M, Hoth S, Koyi H, Kukowski N, Lohrmann J, Ravaglia A, Schlische R W , Withjack M O, Yamada Y, Cavozzi C , DelVentisette C, Elder Brady J, Hoffmann-Rothe A, Mengus J M, Montanari D and Nilforoushan F. 2006. Analogue benchmarks of shortening and extension experiments // Buiter S H and Schreurs G. Analogue and Numerical Modelling of Crustal-Scale Processes. Geological Society, London, Special Publications, 253: 1–27.
Simpson G. 2011. Mechanics of non-critical fold-thrust belts based on finite element models. Tectonophysics, 499: 142–155.
Smit J W, Brun J P and Soukoutis D. 2003. Deformation of brittle-ductile thrust wedges in experiments and nature. Journal of Geophysical Research: Solid Earth, 108 (B10). Doi: 10.1029/2002JB002190.
Stockmal G S, Beaumont C, Nguyen M and Lee B. 2007. Mechanics of thin-skinned fold-and-thrust belts: Insights from numerical models // Sears J W, Harms T A and Evenchick C A. Whence the Mountains? Inquiries into the Evolution of Orogenic Systems: A Volume in Honor of Raymond A Price. GSA Special Publications, 433: 63–98.
Storti F and McClay K. 1995. Influence of syntectonic sedimentation on thrust wedges in analogue models. Geology, 23(11): 999–1002.
Storti F, Salvini F and McClay K. 2000. Synchronous and velocity-partitioned thrusting and thrust polarity reversal in experimentally produced, doubly-vergent thrust wedges: Implications for natural orogens. Tectonics, 19(2): 378–396.
Strayer L M, Hudleston P J and Lorig L J. 2001. A numerical model of deformation and fluid-flow in an evolving thrust wedge. Tectonophysics, 335: 121–145.
Souloumiac P, Maillot B and Leroy Y M. 2012. Bias due to side wall friction in sand box experiments. Journal of Structural Geology, 35: 90–101.
Suppe J. 2007. Absolute fault and crustal strength from wedge tapers. Geology, 35: 1127–1130.
Teixell A and Koyi H A. 2003. Experimental and field study of the effects of lithological contrasts on thrust-related deformation. Tectonics, 22(5): 1054. doi: 10.1029/ 2002TC001407.
von Huene R and Culotta R. 1989. Tectonic erosion at the front of the Japan Trench convergent margin. Tectonophysics, 160(1-4): 75–90.
Wang W H and Davis D M. 1996. Sandbox model simulation of forearc evolution and noncritical wedges. Journal of Geophysical Research: Solid Earth, 101(B5): 11329–11340.
Weijermars R and Schmeling H. 1986. Scaling of Newtonian and non-Newtonian fluid dynamics without inertia for quantitative modelling of rock flow due to gravity (including the concept of rheological similarity). Physics of the Earth and Planetary Interiors, 43: 316–330.
Wenk L and Huhn K. 2013. The influence of an embedded viscoelastic–plastic layer on kinematics and mass transport pattern within accretionary wedges. Tectonophysics, 608: 653–666.
Wigner E P. 1960. The unreasonable effectiveness of mathematics in the natural sciences. Communications in Pure and Applied Mathematics, 13(I): 1–14.
Willett S D. 1999. Orogeny and orography: The effects of erosion on the structure of mountain belts. Journal of Geophysical Research: Solid Earth, 104(B12): 28957–28982.
Willett S D, Beaumont C and Fullsack P. 1993. Mechanical model for the tectonics of doubly vergent compressional orogens. Geology, 21(4): 371–374.
Willett S D and Brandon M T. 2002. On steady states in mountain belts. Geology, 30(2): 175–178.
Willett S D, Schlunegger F and Picotti V. 2006. Messinian climate change and erosional destruction of the central European Alps. Geology, 34: 613–616.
Xiao H B, Dahlen F A and Suppe J. 1991. Mechanics of extensional wedge. Journal of Geophysical Research: Solid Earth, 96(B6): 10301–10318.
Yamato P, Kaus B P, Mouthereau F and Castelltort S. 2011. Dynamic constraints on the crustal-scale rheology of the Zagros fold belt, Iran. Geology, 39: 815–818.
A Review of Tectonic Sandbox Modeling of Fold-and-thrust Belt
DENG Bin1, 2, ZHAO Gaoping1, WAN Yuanbo1, HUANG Rui1, WANG Xinjian1and LIU Shugen1
(1. State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation / Chengdu University of Technology, Chengdu 610059, Sichuan, China; 2. MLR Key Laboratory of Tectonic Controlled Mineralization and Oil Reservoir, Chengdu University of Technology, Chengdu 610059, Sichuan, China)
Brittle deformation in fold-and-thrust belt of shallow crust is generally characterized by a long tectonic history and complex geological features which results from interdependent parameters. Since the 1810s, tectonic sandbox modeling has been a powerful and indispensable tool to help in providing a unified picture of the evolution of deformation in shallow crust with considerable spatial and temporal detail based on self-organization and unreasonable effectiveness of tectonics. Here we review current understandings from tectonic sandbox models of fold-and thrust belt, to help present and future modelers and researchers in understanding of basin-mountain evolution and their dynamics. The classic sandbox models suggest that extensional and shortening deformation in shallow crust follow the critical Coulomb wedge theory, with self-similar growth processes. Furthermore, past practices of sandbox modeling have explored the role of main parameters governing deformation, and these parameters are the properties of basement (geometry, friction, basal coupling, fluid overpressure), the properties of deforming material (geometry, rheology, mechanical layering, inhomogeneity), kinematics (boundary geometry, velocity, obliquity) and surface processes (erosion and sedimentation). It should be noted that the sandbox models have grown increasingly bold in understanding mechanical and structural evolution of fold-and-thrust belt in shallow crust, and inconsistence between models and natural systems are common in parameters such as spatial scale, time scale, material properties, and number of active processes.
sandbox modeling; critical taper; fold-and-thrust belt
P542
A
1001-1552(2016)03-0446-019
2015-01-16; 改回日期: 2015-05-18
邓宾(1980–), 男, 副教授, 博士, 研究方向为含油气盆地分析。Email: dengbin13@mail.cdut.edu.cn
