数形结合思想在初中数学教学中的运用评价

刘子艳

（吉林省长春市农安县鲍家中学　吉林长春　130209）



数形结合思想在初中数学教学中的运用评价

刘子艳

（吉林省长春市农安县鲍家中学吉林长春130209）

作为抽象学科的代表，学生在学习数学的过程中由于缺乏空间想象的能力使得在学习起来十分吃力。为更好的掌握这门体现空间形式和表达数量之间相互关系的学科，将枯燥无味的数字、方程式与具体的图形相结合，加深学生的理解，以便更好的运用。数字与形态相结合的教学方法，加深空泛的数字与具体的图形的结合，使原本复杂的数字更好的转化为简单的空间图形，便于学生的理解学习的一种数学教学方法。

初中 数学教学 数形结合思想 效果

日常初中学生的数学教学过程中，由于学生年纪尚小，其思维方式和思维能力还没有形成。而数学又是一门由数量关系和空间形式构成的学科，思维能力的培养对于学好数学有十分重要的意义［1］。数字与空间图形相结合的数学思想，通过生动的图形对空泛的数字进行解释，同时精确的数字也给抽象的图形以支撑，这种数学思想在数学教学中能更好地解决数学问题，有利于学生数学思维的形成，有利于以后数学更高难度的学习，同时对于其余学科的学习也有帮助。

一、什么是数形结合思想

数学作为一门被广泛运用的自然科学，主要包括两大方面的内容。一是用基本的文字所阐述的数学概念、公理及定理和一些数学公式和算法，其都是由具体的问题或数字构成，这称之为数学的“数”；二是由具体的二维平面图像，三维立体图像，由点、线、面、空间构成的称之为数学的“形”。由于数学的“数”采用数字和文字进行描述难以理解，这时数学的"形"就能巧妙的对其加以补充和解释，有利于学生的理解；同时，某些抽象的数学图形，结合具体的数字文字也使图像更加清晰，不再晦涩难懂。在学生学习数学过程中，掌握数形结合思想对于理解数学基本概念，很好的对数学知识进行熟练作用大有裨益。同时图形对概念的具体阐述，使得原来枯燥的概念也更加具体清楚。数学概念，定理公理等是对复杂的数学推理过程的结果的提炼简化，由于只有短短几十个字，学生通过这些文字想完全理解其中蕴含的科学道理十分困难，采用数形结合思想能够使学生更好的理解数学这门语言精炼但意蕴丰富的学科，也使其中的科学内涵更加充分的显现出来［2］。

二、数形结合思想渗透于教学各个方面

1.在书本中的运用

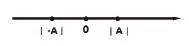
在数学课本中，常常有大量的概念、公理、定理等等，为了使同学更好的理解这些知识，编写课本的编者都会为其配一些图形方便学生的理解。如勾股定理的学习中采用直角三角形举例进行阐述；在追击相遇问题中，采用作图法进行表述；在学习绝对值和相反数时，采用在数轴上进行标识，帮助学生理解其概念。

2.在教学中的运用

在教学过程中，许多同学的空间想象能力欠缺，导致其理解问题片面，考虑不周全。考虑问题容易漏掉，使结果片面。这时，教师在教学中采用数形结合思想对于学生理解问题能力的提高有很大好处，例如立方体表面积体积计算中采用实际物体，如豆腐块，橡皮等进行切割，方便学生们的理解到底表面积增多减少了多少，减少了漏掉问题某些方面的可能性。

3.对于学生的提高

书本和教学的最终目的都是为了能让学生掌握知识，并且能形成自己的数学思维，在遇到问题时，懂得采取数形结合思想来解决问题。教育的目的是为了让学生自己解决问题，数形结合思想能使学生遇到疑难问题时，通过图形进行问题表述，结合具体文字，解决问题。比如在不等式的运算中，可以先将不等式（x-3）（x+1）＜0当做等式（x-3）（x+1）=0进行计算，求得x=-1 x=3之后，再作图进行表示，求得不等式的解集。这样不仅培养了学生的数形结合思想，同时也减少了出错率，提高学生解题的正确率。这种数形结合思想在解决数学问题中不仅简单明了，同时也向学生充分展示数形结合思想解决问题的便捷性，使学生在解决问题中能更多的运用这种方法。

三、总结

初中学生的数学思维尚未完全形成，解决数学问题有很大的局限性。由于初中学生刚由小学数学过渡过来，解决问题仍然停留在简单的字面之上，培养他们的思维解决问题的能力，不仅有利于学生解决数学问题，也有利于学生在解决其他学科问题上思维的拓展。数形结合思想是一种新型教学理念，老师在授课过程中采用简单难懂的数字与具体清晰的图形相结合，不仅对于基本概念有更加准确的说明，同时图像的使用也使授课形式不再单一，更加多样化，调动了学生的积极性。老师在授课时候，应该有意识地建立所教授学生的数形结合思想。⑴向学生展示数形结合对于解决数学问题的益处；⑵在数学学习中，首先接触到的数学概念数学定理等知识枯燥无味，要引导学生用图形加深对概念的理解，帮助他们进行记忆，理解概念背后的数学意义，而不是只是理解字面意思。⑶学习数学的目的是为了运用，让学生能更好的自主解决所遇到的问题，因此，在教学中，教师应该有意识的指导学生在解决问题时采用多种方式，进行多种尝试，培养他们的思维。⑷图形的规范性对于结果有很大的影响，教师在示例数形结合思想时候，应该注意作图的规范性，图形的正确表达能使问题更加利于解决。若图形表述错误，不仅不能解决问题，反而能使自己陷入另一个僵局之中。⑸思维的建立，有利于学生日后各种问题的解决中更加全面的分析问题［3-4］。

综上所述，数形结合思想对于初中学生的数学学习有十分积极的意义。教师采用数形结合思想不仅能使课堂更加丰富多彩，也能使学生更好的理解并掌握所学知识；对于学生来说，数形结合思想有利于学生解决问题的思维创建，考虑问题更加全面，能更好的解决问题，理解性的掌握所学知识，使学习更加轻松高效。

［1］郭发权.小议数形结合思想在初中数学教学中的应用［J］.考试周刊，2016，02（2）：61-61.

［2］林卫.数形结合思想在初中数学教学中的实践研究［J］.数学学习与研究：教研版，2016，01（2）：36-36.

［3］高爱红.数形结合思想在初中数学教学中的应用研究［J］.数学教学通讯，2016，10（2）：37-38.

［4］叶学瑾.初中数学教学中数形结合思想的应用［J］.教育，2015，05（34）：94-94.