基于排序集样本和辅助变量中位数的均值比率估计方法

乔松珊，张建军，孙成金

(1.中原工学院 信息商务学院，河南 郑州 450007；2.河南农业大学 信息与管理科学学院，河南 郑州 450002)



基于排序集样本和辅助变量中位数的均值比率估计方法

乔松珊1，张建军2，孙成金2

(1.中原工学院 信息商务学院，河南 郑州 450007；2.河南农业大学 信息与管理科学学院，河南 郑州 450002)

摘要：排序集抽样下利用辅助变量中位数构建了总体均值的改进比率估计模型，分析了该比率估计量的偏差和均方误差，并与简单随机抽样下的比率估计比较，证明了改进后的比率估计均方误差更小。以农作物播种面积和产量为研究对象进行实例分析，研究表明，基于排序集样本和辅助变量中位数的比率估计方法可以有效提高估计精度，验证了该构造方法的可行性。

关键词：辅助变量；中位数；排序集样本；比率估计

一、引言

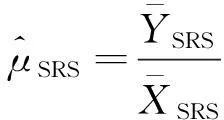
(1)

比率估计并不是无偏估计，为了降低估计偏差，提高精度，一些学者探讨了两种改进思路，一是修改估计量形式，二是采用新的抽样方法。Sisodia、Singh和Yan等人分别利用辅助变量的变异系数，峰度系数和偏斜系数，在随机抽样下提出了均值比率估计的改进形式[2-4]，随后Subramani等人为了提高估计量的稳定性，在前人研究基础上提出了另一种比率估计量[5]：

(2)

(3)

其中θ=μX/(μX+Md)。研究结果表明，相关系数满足一定条件时，该估计量的估计效率要比上述其它几种改进形式精度更高。

排序集抽样(RSS)是一种新的抽样方法，最初是由McIntyre在估计牧草产量时提出，随后得到了深入研究和广泛应用[6]；Dell等指出当样本易于排序而不容易具体测量时，基于排序集抽样方法可以提高均值估计的精度[7]；Stokes分析了排序集抽样下方差的估计方法，证明了样本方差为总体方差的渐进无偏估计[8]；Chen讨论了排序集抽样下参数极大似然估计的相合性和渐进正态性，并与随机抽样相比，分析了估计的相对渐进效率[9]。另外，在均值比率估计方面也有不少研究成果：Samawi在排序集抽样下讨论了总体均值的比率估计问题，并与随机抽样相比，说明了基于排序集样本的比估计有效降低了估计的均方误差[10]；Kadilar等通过增加比率系数，利用排序集样本对传统估计形式进行改进，并讨论了比率系数的确定方法[11]；Jozani等研究了排序集抽样下降低比率估计偏差的方法，提出了总体均值的无偏和近似无偏比率估计形式，并分析了估计量的均方误差[12]；AI-Omari基于辅助变量一、三分位数构造均值的比率估计量，并比较了两种抽样方法下的估计方差[13]。

辅助变量信息的利用程度直接影响均值估计的精度，为此，本文同时考虑排序集样本和辅助变量中位数两个因素，构造总体均值改进的比率估计形式。首先，提出总体均值的改进比率估计形式，并讨论估计量的近似无偏性和均方误差；其次，通过比较两种抽样方法下估计量的均方误差，证明了改进比估计量的有效性；最后，通过实例进一步分析得出结论。

二、改进的比估计量及性质

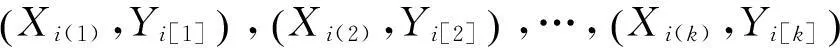
在进行均值比率估计时，如果还有其它辅助信息可以利用，我们希望在降低估计偏差的同时，进一步降低估计量的均方误差。与辅助变量的变异系数、峰度和偏度系数相比，中位数不容易受到极值和异常值的影响，有鉴于此，本文受到式(2)构造方法的启发，尝试同时考虑排序集样本和辅助变量中位数建立均值μY的改进比率估计模型，构建模型如下：

(4)

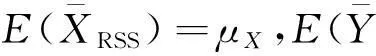
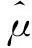
(5)

(6)

下面,计算排序集抽样下改进比率估计的均方误差。首先，利用Samawi中的结论，得到引理1。

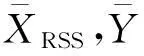
(7)

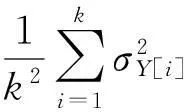
(8)

同理可得：

(9)

(10)

将式(8)、(9)、(10)代入式(7),整理得到：

(11)

其中θ=μX/(μX+Md),TX(i)=μX(i)-μX,TY[i]=μY[i]-μY,TXY(i)=TX(i)TY[i]。

(12)

其中相应参数表达式与式(11)相同。

三、改进估计量的有效性

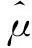
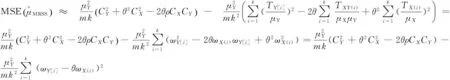
定理3表明，利用排序集样本代替随机样本的改进比率估计有效地降低了估计的均方误差，也即基于排序集样本的估计效率要高于随机抽样下的估计效率。

四、实例分析

选取2014年河南省28个市(县)的粮食播种面积和粮食产量为研究总体，其中研究变量Y是粮食产量，辅助变量X为播种面积，数据如表1所示。

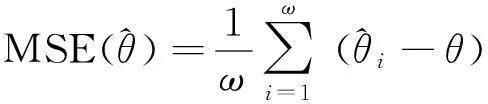
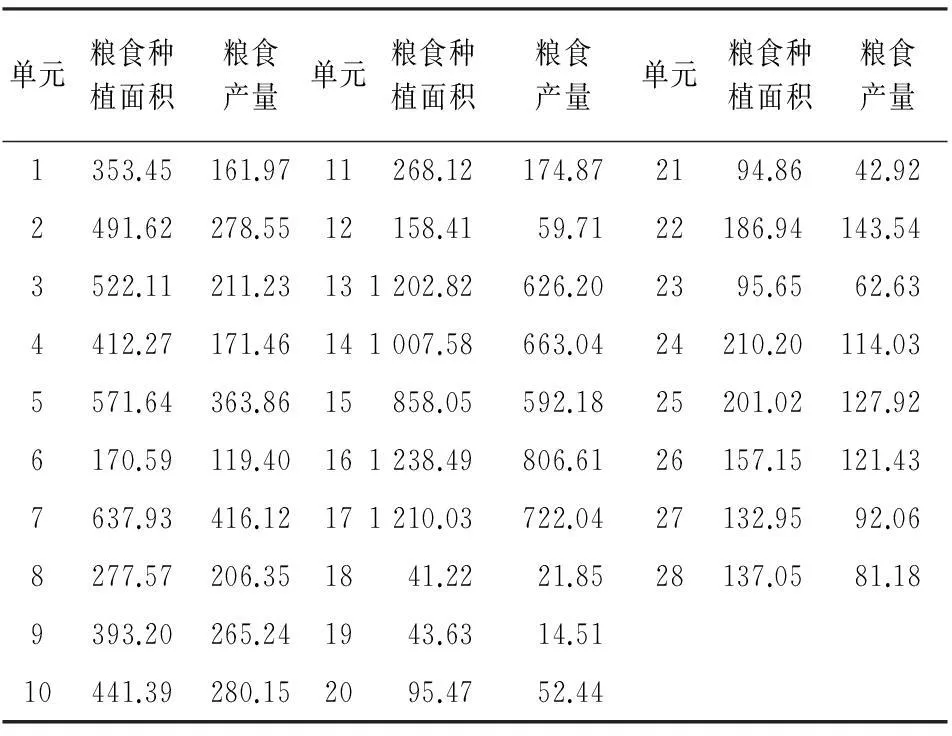
表1　研究总体的相关数据

注：数据来源于《河南省统计年鉴》。单元指总体单元，粮食种植面积为千公顷，粮食产量单位为万吨。

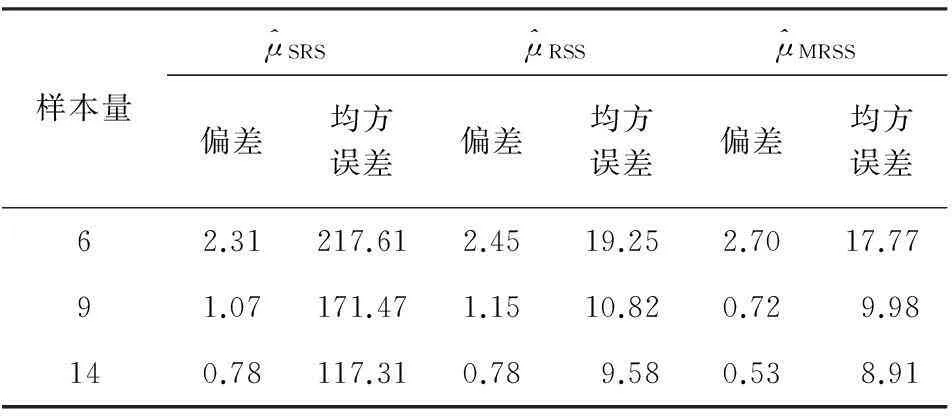
表2　不同比估计量的估计结果比较

表2给出了不同比率估计的偏差和均方误差，从计算结果容易看出：其一，两种抽样下比率估计的偏差都随着样本量的增加不断变小，改进后的比率估计变化更加明显；其二，排序集抽样方法有效利用了辅助信息，通过排序筛选得到样本进而计算估计值，因此，整体上估计的均方误差较随机抽样有大幅度降低，说明该方法的估计结果稳定性较好；其三，与单一基于排序集样本的比率估计相比，文中提出的改进比率估计的均方误差进一步降低，并且随着样本量的增加，比率估计效率不断提高。

五、结论

抽样方法设计和估计量设计是提高均值比率估计的两个重要手段，由于辅助变量中位数不容易受到数据极值和异常值的影响，而排序集样本可以提高抽样效率，为此，同时考虑这两个方面，基于排序集样本和辅助变量中位数构造了均值的比率估计模型，并进一步研究了估计量的偏差和估计方差。最后，借助实例做了进一步分析比较，验证了模型建立的可行性。排序集抽样下的其它比率估计形式，未来可对它做进一步研究。

参考文献：

[1]杜子芳.抽样技术及其应用[M].北京:清华大学出版社,2005.

[2]Sisodia B V S，Dwivedi V K. A Modified Ratio Estimator Using Coefficient of Variation of Auxiliary Variable[J]. Journal Indian Society of Agricultural Statististics,1981, 33(1).

[3]Singh H P， Tailor R. Use of Known Correlation Coefficient in Estimating the Finite Population Means[J]. Statistics in Transition, 2003,6(4).

[4]Yan Z， Tian B. New Separate Ratio Estimators Using Coefficient of Skewness of Auxiliary Variable[J].Journal of InnerMongolia University of Technology,2011,30(3).

[5]Subramani J, Kumarapandiyan G. New Modified Ratio Estimator for Population Mean When Median of the Auxiliary Variable is Known[J]. Pakistan Journal of Statistics and Operation Research, 2013(2).

[6]McIntyre G A. A Method of Unbiased Selective Sampling Using Ranked Sets[J]. Austral Journal of Agricultural Research,1952 (3).

[7]Dell T R, Clutter J L. Ranked Set Sampling with Order Statistics Background[J].Biometrics,1972,28(2).

[8]Stokes S L. Estimation of Variance Using Judgment Ordered Ranked Set Samples[J].Biometrics,1980,36(1).

[9]Chen Z. The Efficiency of Ranked-set Sampling Relative to Simple Random Sampling Under Multi-parameter Families[J]. Statistica Sinica, 2000,10(1).

[10]Samawi H M. Estimation of Ratio Using Rank Set Sampling[J].Biometrical Journal,1996,38(6).

[11]Kadilar C, Unyazici Y, Cingi H. Ratio Estimation for the Population Mean Using Ranked Set Sampling[J]. Statistical Papers,2009,50(2).

[12]Jozani M J, Majidi S. Unbiased and Almost Unbiased Ratio Estimators of the Population Mean in Ranked Set Sampling[J].Statistical Papers,2012,53(3).

[13]A1-Omari A I．Ratio Estimation of Population Mean Using Auxiliary Information in Simple Random Sampling and Edian Ranked Set Sampling[J].Statistics and Probability Letters,2012,82(11).

(责任编辑：李勤)

收稿日期：2015-12-14

基金项目：河南省高等学校青年骨干教师资助项目《辅助信息在分层比率估计中的应用研究》(2014GGJS-158)；河南省教育厅科学技术研究重点项目《排序集样本在分层抽样中的应用模型与方法研究》(13B110057)

作者简介：乔松珊，女, 河南许昌人，硕士，副教授，研究方向：应用数学；

中图分类号：O212.2∶F301.24

文献标志码：A

文章编号：1007-3116(2016)07-0011-05

The Ratio Estimation of the Population Mean Based on Ranked Set Sample and Median of the Auxiliary Variable

QIAO Song-shan1,ZHANG Jian-jun2,SUN Cheng-jin2

(1. College of Information and Business， Zhongyuan Institute of Technology, Zhengzhou 450007, China 2.Collage of Information and Management Science， Henan Agricultural University, Zhengzhou 450002, China)

Abstract:The paper deals with a new ratio estimator of population mean based on ranked set sample when the median of auxiliary variable is known. The mean squared error and bias of the proposed estimate are derived. It is proved that the modified estimator under ranked set sampling is more efficient than the ratio estimate under simple random sampling. Finally, a practical application about the area and yield of crops is analyzed. From the numerical study it is observed that the new ratio estimator using ranked set sample and median of the auxiliary variable improve the precision of estimation effectively, It is also showed that the proposed modified ratio estimator is feasibility.

Key words:auxiliary variable; median; ranked set sample; ratio estimation

张建军，男，河南开封人，硕士，讲师，研究方向：数理统计；

孙成金，男，山东临沂人，硕士，讲师，研究方向：应用数学。

【统计理论与方法】