基于小波变换的轮轨垂向力信号降噪

黄　辉，雷晓燕，刘庆杰

(华东交通大学 铁路环境振动与噪声教育部工程研究中心，南昌 330013)



基于小波变换的轮轨垂向力信号降噪

黄辉，雷晓燕，刘庆杰

(华东交通大学 铁路环境振动与噪声教育部工程研究中心，南昌 330013)

摘要：轮轨力应变信号在采集过程中，由于噪声干扰的存在，将严重影响所采集数据的准确性。针对轮轨力应变信号中存在的基线漂移和随机白噪声，提出基于小波变换的去噪方法：采用db 6小波基，根据小波多分辨率分析理论，以大尺度分解的逼近分量估计基线漂移成分，从而消除基线漂移；对于随机白噪声则是运用小波阈值去噪法，先根据离散有限序列的自相关函数确定小波分解的最优分解层数，然后采用最小最大阈值以及硬阈值函数，从而实现对白噪声的滤除。仿真与实测数据分析都表明该去噪法能达到比较理想的效果。

关键词：声学；轮轨力；小波变换；去噪；基线漂移；白噪声

基于钢轨应变的测力钢轨法是目前测量轮轨力的主要方法之一，如剪力法、轨腰压缩法等，先在钢轨上粘贴应变片，然后将应变片按一定的方式进行组桥连接，当列车经过时，应变采集仪可采集钢轨应变的组桥输出，再通过对特定的点进行标定，获取标定系数后进而求得轮轨力。然而，在采集应变信号的过程中，干扰因素众多，桥路电压和应变片绝缘电阻的变化，钢轨的支承条件的不确定性，如吊枕、扣件松弛等，加之测试现场复杂的环境干扰，都会使得应变采集仪采集到的应变信号不可避免地含有噪声，这些噪声主要包括两类[1]，一是基线漂移，二是随机白噪声。两种噪声交织在一起使得测试结果与实际情况产生很大偏差，严重干扰信号的量化分析。因此，为有效提高测试结果的准确性，就必须对受噪声污染的信号进行处理。

基线漂移和白噪声的降噪在国内外已有大量研究。基线漂移的消除是医学领域中信号处理的经典问题，如心电图信号、脉搏信号等，主要的消除方法有曲线拟合[2]，中值滤波[3]、小波变换滤波[4]等。除了在医学领域基线漂移的消除有广泛研究外，在地震监测[5]、电磁勘探[6]等领域也针对基线漂移的消除进行了相关研究。白噪声在测试中则是较为普遍的存在，传统的消除方法是基于傅里叶变换的带通滤波来实现，但有用信号易被当成噪声一并滤掉，因此降噪效果并不明显。近些年来，小波阈值降噪正得到更为广泛地研究与应用[7,8]。

本文针对轮轨力应变信号中的主要噪声，提出了一种基于小波理论的综合去噪法：先对信号进行大尺度分解，最大限度地消除基线漂移，在此基础上，引入噪声的白化检验法确定最优分解层数，再利用小波阈值去噪法去除白噪声。

1　小波变换与Mallat算法[9]

1.1小波变换

设L2(R)是R上平方可积函数构成的函数空间，f(t)为能量有限的信号，f(t)∈L2(R),如果ψ(t)∈L2(R),且其傅里叶变换满足容许性条件

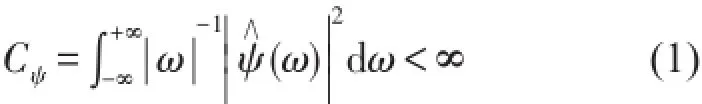
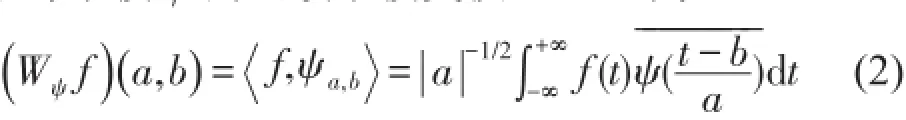
则称ψ为一个基本小波或者母小波。信号 f(t)关于母小波ψ的连续小波变换（CWT）为式中ψˉ是对ψ的共轭运算，a,b∈R,且a≠0。a称为伸缩因子，b称为平移因子。式(2)对应的逆变换为

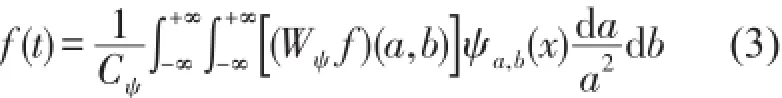
小波变换把原来的一维信号变成二维信号，而小波逆变换则把二维信号重构回原来的一维信号。

连续小波变换主要用于理论分析与论证，在实际问题的数值计算中常采用离散形式。取连续小波变换中的伸缩因子和平移因子为，代入式(2)得离散小波变换（DWT）为

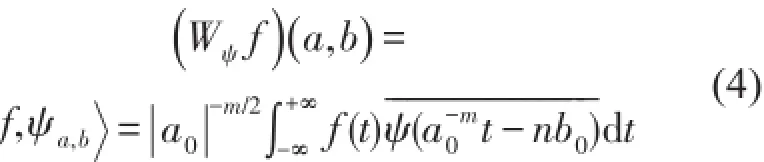
1.2 Mallat算法

1988年S.Mallat从空间的概念出发，提出了多分辨分析的概念。1989年，Mallat受小波变换多分辨率分析理论与图像处理的应用研究中的塔式算法的启发，提出了信号的塔式多分辨率分析分解与重构的快速算法，即著名的Mallat算法。Mallat算法在小波变换中的地位之于快速傅里叶变换（FFT）在傅里叶分析中的地位。

Mallat算法的基本原理就是将信号在不同的尺度下分解成逼近信号和细节信号，若以S表示原始信号，Ai(i=1,2…,m)表示逼近信号，Di(i=1,2…,m)表示细节信号，则Mallat算法分解如图1(a)所示。分解算法的逆变换对应于重构算法，即将最终的逼近信号和细节信号恢复成原始信号，如图1(b)所示。

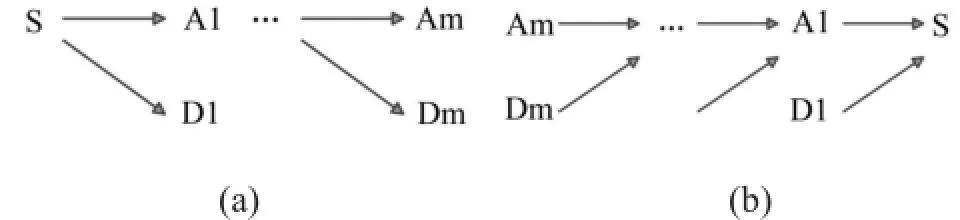
图1　Mallat算法分解与重构

2　降噪实现

2.1小波基选择

小波分析应用中的小波基的选择是个热点问题，也是个难点问题，在选择时并没有统一的标准，不同的小波基在降噪效果方面可能相差甚远。因此，在实际应用时应具体情况具体分析。

目前，小波基的选择主要从正交性、紧支性、光滑性、对称性及消失矩等五个要素来考虑。在选择小波基时希望尽可能满足上述五个要素，但这样的小波基是不可能存在的，例如紧支性和高消失矩就是一对矛盾。在工程降噪领域，常用的小波基有db N系列小波和sym N系列小波，作者使用这两种系列小波基结合实际轮轨力应变信号，经过反复试验滤波及信号重构决定在消噪法中使用db 6小波基。

2.2基线漂移去除

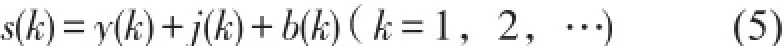
应变采集仪采集到的轮轨力应变信号数据可以表示为式中s(k)为应变采集仪采集到的数据，y(k)为有效的钢轨应变信号数据，j(k)为信号中包含的基线漂移数据，b(k)为信号中的白噪声数据。

基线漂移成分 j(k)频率通常较低，表现为一个缓慢变化的过程，在应变信号采集时会引起信号基线位置的上下漂移，使得信号严重失真。

根据小波变换的多分辨率分析理论，信号可进行逐级多层分解，每层分解都可得到逼近信号和细节信号，其中，每一层的逼近信号是相对于上一层逼近信号的相对低频部分，而每一层的细节信号是相对于上一层逼近信号的相对高频部分。由于基线漂移成分的频率很低，可对信号进行大尺度分解，将分解的最后一层信号中的逼近部分作为对基线漂移的估计，从原始信号中去除这部分信息后重构，即可实现对基线漂移的矫正。

2.3白噪声去除

将式(5)中的基线漂移成分 j(k)去除后，含噪信号模型可以表示为

s(k)=y(k)+b(k)（k=1，2，…)(6)

使用阈值降噪法对白噪声b(k)进行去除，其基本理论是：有用信号通常存在于低频，噪声信号存在于高频，信号经过小波分解后，有用信号的小波系数较大，而噪声的小波系数较小，因此可以设置一个合适的阈值，当小波系数的绝对值大于阈值时予以保留或做收缩处理，当小波系数的绝对值小于阈值时设置为零，从而达到去除噪声的目的。

(1)白噪声检验确定最优分解层数

在降噪过程中，分解层数的确定很重要，过多或过少的分解层数都会导致降噪效果的不理想。用自相关函数的估计来检验白噪声[10]，从而确定分解层数。

设离散有限序列为r(i)(i=1,2,…,N)，其自相关函数的估计式为

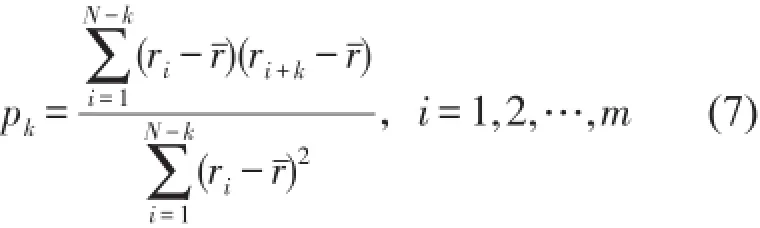
为消除式(6)中的白噪声b(k)，对含噪信号s(k)进行小波分解，每分解一层，就取该层的细节分量进行白噪声检验，若通过检验，则进行下一层分解，重复上述步骤，如果分解到第z层时，该层的细节分量不能通过白噪声检验，则最终将分解层数定位为z-1层。

（2）阈值估计与阈值函数的选择[11]

目前，主要的阈值估计有：通用阈值、无偏释然估计原理的自适应阈值、混合型阈值、最小最大准则阈值。四个阈值规则中，虽然最小最大准则阈值估计较为保守，但能很好地减少有效信息的损失，因此本文采用最小最大准则阈值。

阈值函数最常用的有硬阈值函数和软阈值函数，硬阈值函数对小波系数进行处理后会使得信号的光滑性一般，但相对于软阈值函数来说，其能减少有用信息的损失，因此采用硬阈值函数。

2.4降噪算法流程

轮轨力应变信号中的基线漂移和白噪声的降噪算法流程如图2所示。

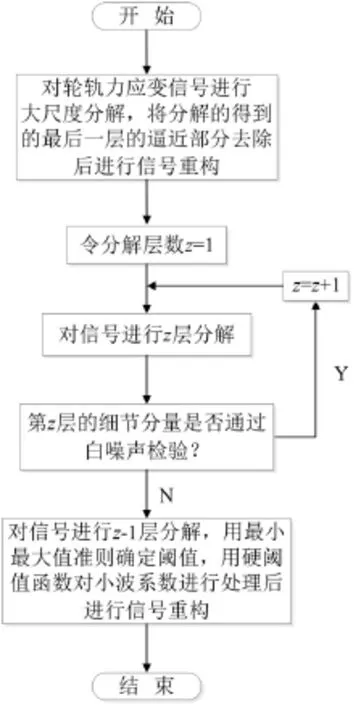
图2　降噪算法流程

3　仿真实验

利用有限元分析软件ANSYS建立钢轨模型并模拟施加车轮荷载，按照剪力法的组桥方式对钢轨应变进行组桥输出，得到一段如图3(a)所示的理想轮轨力应变信号，理想轮轨力应变信号没有基线漂移和白噪声。

加入频率为0.2 Hz，幅值约为理想信号峰峰值1/10的正弦波作为基线漂移成分，然后再加入随机白噪声构成含噪信号，如图3(b)所示。为保证添加噪声后的信号和理想信号的数据有相同区间长度，基线漂移和白噪声数据的采样频率与理想信号的采样频率都为2 000 Hz，采样时间都为7 250 ms。

对于图3(b)中的含噪信号，先根据小波多分辨率分析理论进行基线漂移的消除，利用Mallat算法对信号进行分解，表1为进行12层小波分解后信号的频率分布，Di(i=1,2…,12)为各层的的细节分量，A12为第12层的逼近分量，从表中可以看出，A12对应的频率范围大约为0～0.24 Hz，而基线漂移成分的频率为0.2 Hz，因此只需将逼近分量A12进行滤除便可实现对基线漂移的矫正，去除基线漂移后进行信号重构得到如图3(c)所示的信号。之后进行白噪声去除，由白噪声检验得到的最优小波分解层数

为3层，用小波阈值法对白噪声进行滤除后进行信号重构，便完成了整个消噪过程。图3(d)为去噪后的信号，从图中可以看出，基线漂移得到了较好的矫正，白噪声也得到了较好的抑制，且与原始的理想信号相比，去噪后的信号能很好地保持原有信号的波形特征。

为了检验信号降噪后的效果，用信噪比(SNR)和均方根误差(RMSE)进行评价。信噪比越高，均方根误差越小，则降噪效果越好。式中S(i)为原信号，S∧(i)为降噪后的信号。

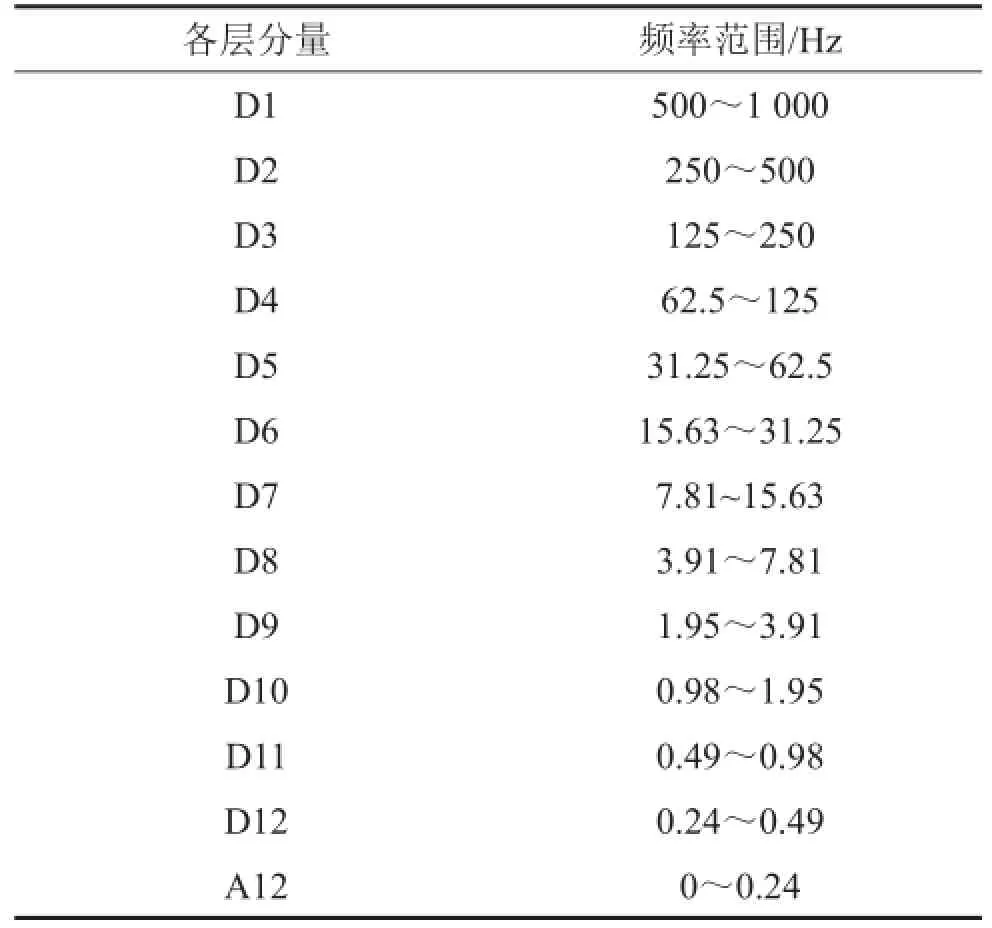
表1　信号频率分布

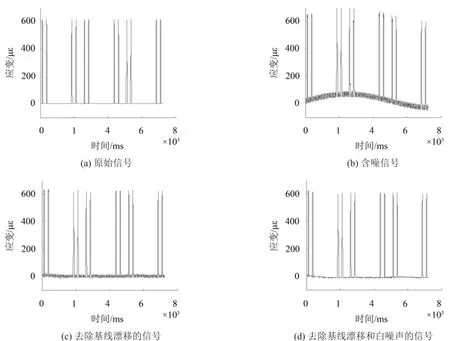
图3　仿真轮轨力应变信号及降噪

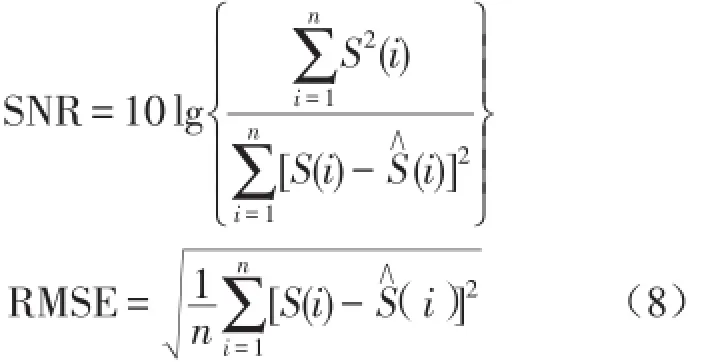
表2给出了含噪信号和去除基线漂移和白噪声信号的SNR值和RMSE值，从表中可以看出，去噪信号的SNR值明显提高，而RMSE值则明显降低，这充分说明了去噪方法的有效性。

表2　信号消噪前后比较

4　应用实例

选取的数据为在江苏省宁启线上测试时的一段轮轨力应变数据，如图4(a)所示。测试时所采用的贴片方式为剪力法，数据的采样频率为1 000 Hz。

从图4(a)中可以看出，原始信号较为明显地偏离了零基准线，而且数据中夹杂的随机白噪声使得信号看起来略显粗大。对信号进行9层分解，将第9层上的逼近分量A9(0～0.98 Hz)作为对基线漂移的估计，对其作置零处理后进行信号重构得到如图4 (b)所示的去除基线漂移后的信号。将图4(b)所示的信号进行白噪声检验得到的最优小波分解层数为6层，用阈值法降噪后进行信号重构得到如图4(c)所示的信号。从图4(c)可以看出，降噪后信号波形能很好地保留，基线漂移得到了非常明显的改善，白噪声也被很好地去除，去噪效果比较理想。基线矫正的目的。对信号中的白噪声则是先通过离散有限序列的自相关函数的估计来确定最优分解层数，然后采用最小最大准则对阈值进行估计，采用硬阈值函数对小波系数进行处理，从而实现对白噪声的抑制。通过仿真实验与实例分析，都说明了本文的去噪法效果明显。在今后基于钢轨应变的轮轨力测试中，该方法可为信号去噪提供一定的参考。

参考文献：

[1]农汉彪.轮轨垂向荷载连续测量与识别方法研究[D].成都：西南交通大学，2011.

[2]全晓莉，古良玲，赵明富.一种消除脑血流信号中基线漂移的新方法[J].微计算机信息，2009，25(1-1)：309-311.

[3]蔡坤，陆尧胜.基于中值滤波的心电基线校正方法的研究[J].医疗设备信息，2004，19(2)：5-7.

[4]任杰，杨晓丽.基于小波变换系数的心电信号基线漂移噪声去除方法[J].医疗卫生装备，2010，31(11)：24-26.

[5]李吉涛，杨庆山.地震波基线漂移的处理方法[J].北京交通大学学报，2010，34(1)：95-99．

[6]李肃义，林君，阳贵红，等.电性源时域地空电磁数据小波去噪方法研究[J].地球物理学报，2013，56(9)：3145-3152.

[7]袁弘倩，姚加飞，杨扬，等.抗噪声源物理噪声引起的尖峰噪声的抑制[J].噪声与振动控制，2015，35(1)：195-199.

[8]李琳，张永祥，刘树勇.改进EMD-小波分析的转子振动信号去噪方法[J].噪声与振动控制，2015，35(2)：170-174.

[9]张德丰.MATLAB小波分析[M].北京：机械工业出版社，2009.

[10]李炜，陈晓辉，毛海杰.小波阈值消噪算法中自适应确定分解层数研究[J].计算机仿真，2009，26(3)：311-313.

[11]张臣国.小波分析在信号降噪中的应用研究[D].成都：电子科技大学，2012.

国家自然科学基金项目（51368021）；江西省优势科技创新团队计划项目（20133BCB24007）

向：铁路环境振动与噪声。E-mail:844513293@qq.com

铁路环境振动与噪声。

E-mail:xiaoyanlei2013@163.com

中图分类号：O422.6

文献标识码：A

DOI编码：10.3969/j.issn.1006-1335.2016.01.022

文章编号：1006-1355(2016)01-0101-05

收稿日期：2015-05-17

基金项目：国家自然科学基金项目(51478184)；

作者简介：黄辉（1991-）男，江西大余人，硕士研究生，研究方

通讯作者，雷晓燕（1956-）男，教授，博士生导师，研究方向：

De-noising of Vertical Wheel-rail Contact Force Signals Using
Wavelet Transform

HUANGHui,LEI Xiao-yan,LIU Qing-jie

(Engineering Research Center of Railway Environmental Vibration and Noise,Ministry of Education, East China Jiaotong University,Nanchang 330013,China)

Abstract:The accuracy of the wheel-rail strain signals can be seriously ruined by the disturbance of noise.In this paper,a denoising method based on wavelet transform was proposed for elimination of baseline drift and random white noise.The baseline drift was eliminated by using db6 wavelet bases and the estimation of high-1evel approximation based on wavelet multi-resolution analysis.While the random white noise was eliminated by applying wavelet threshold denoising method.First of all,the optimal decomposition level of the wavelet transformation was determined by applying the selfcorrelation function of discrete finite sequence.Then,the minimum and maximum thresholds and hard shrinking function were adopted to filter the white noise.The analysis of simulation and the measured data show that this denoising method can achieve ideal effect.

Key words:acoustics;wheel-rail contact force;wavelet transform;de-noising;baseline shift;white noise