PSO_SA算法在水下结构激励力源识别中的应用
2016-08-04商德江
肖 妍, 商德江
(1. 哈尔滨工程大学 水声工程学院,哈尔滨 150001;2. 哈尔滨工程大学 水声技术重点实验室,哈尔滨 150001)
PSO_SA算法在水下结构激励力源识别中的应用
肖妍1,2, 商德江1,2
(1. 哈尔滨工程大学 水声工程学院,哈尔滨150001;2. 哈尔滨工程大学 水声技术重点实验室,哈尔滨150001)
提出一种识别水下弹性结构内部激励力源的匹配场处理方法,建立基于辐射声场的广义拷贝场概念,并提出采用粒子群模拟退火融合搜索算法对最优力源强度进行匹配搜索。以水下自由声场中的单层圆柱壳体作为研究对象,对声压传递函数进行了数值计算,针对激励力源识别匹配场处理方法进行了数值仿真分析;在消声水池中进行了水下单层圆柱壳体结构振动与辐射声场测试,将测试结果与拷贝场进行匹配处理,搜索最优力源强度,并以该搜索结果进行了圆柱壳体辐射噪声预报。仿真结果与试验结果均表明,这种方法可以有效的针对结构内部的力源强度进行分析排序;同时,利用匹配识别的结果进行辐射噪声预报时,预报精度很高。
水下结构;力源强度;匹配场处理;粒子群模拟退火算法
针对水下结构的噪声源识别问题,国内外学者开展大量的理论研究与试验研究,形成了多种噪声源识别方法。例如,基于多输入/输出模型的噪声源分析方法、自适用噪声抵消法、功率流分析方法、基于状态空间的系统辨识方法及盲信号处理技术等[1-3]。此外,声强测试技术[4]及声全息测试技术[5]也广泛应用于水下结构噪声源识别中。利用声强测试技术和声全息测试技术进行水下结构噪声源识别是有效的,但是对测量要求比较高,声场环境边界条件对反演的精度和稳定性有较大的影响,接收基阵的设计加工难度也较大。最主要的是,这些噪声源识别技术,仅仅是根据结构表面源强度的大小来进行判定,无法对结构内部的力源进行有效分析。本文针对水下弹性结构内部噪声源(力源)识别技术,开展了匹配场处理方法研究。
匹配场处理是一种新的水声信号处理方法,它是近年来水声信号处理领域研究的热点。匹配场处理技术近年来在水下目标检测、被动定位、海洋环境声学参数反演等方面的应用受到广泛的关注[6-8]。本文借鉴了这种水声匹配处理的概念,将其应用于水下结构力源识别中,改变了以往只能对结构表面源强度进行分析的现状,可以针对结构力源进行更有效的分析。其基本思想是:将水下结构及声场作为“信道”、激励源频率特性作为“输入”、水下结构受激振动产生的声辐射特性作为“输出”,通过数值分析方法建立由传递函数计算得到的“广义拷贝场”。将实际测量的声场与拷贝场进行相关匹配处理,找到与实际测量声场最接近的传递函数拷贝场,确定其所对应的结构力源的位置、贡献量等信息,从而进行水下结构噪声源识别。
1力源识别匹配处理方法基本原理
针对水下弹性结构,对其内部的激励力源进行匹配识别时,主要有声压拷贝场、振速拷贝场、辐射声功率、声辐射效率等几种匹配物理量,可根据具体的匹配物理量选择相应的目标函数[9]。以声压拷贝场为例,匹配算法的具体流程见图1。
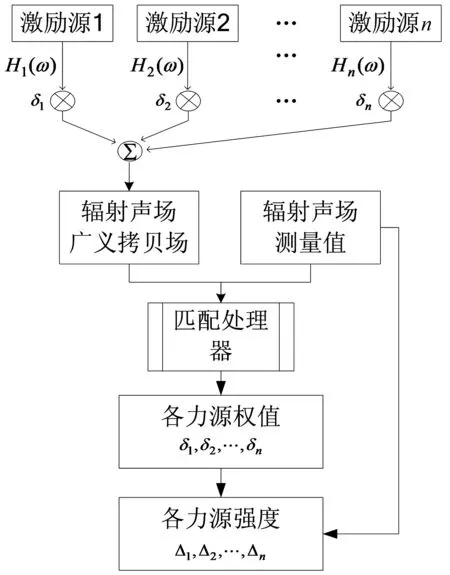
图1 激励力源强度识别匹配处理流程图Fig.1 The flowchart of exciting force source identification by MFP
具体实现方法如下:
首先建立结构体的数值模型,假设模型内部共有n个非相干激励力源,外部声场中有m个声压测点(m≥n)。第i个激励源的响应函数为Fi,力源强度为Δi。声场中第j个声场测点处的声压值为Pj,第i个激励源至第j个声场测点处的声压传递函数记为Hij(1 ≤i≤n,1 ≤j≤m)。
其中Fi、Pj和Hij的关系如下:
(1)
对结构受力源激励下的辐射声场进行数值预报[10]。根据数值预报结果,计算出各力源至各场点处的声压传递函数Hij,假设各力源强度之间的比例系数为δi(0 ≤δi≤ 1),计算得出声场总传递函数:
(2)
从式(1)和式(2)中可以得出δi与Δi的关系:
(3)
则由不同δi组合形式计算形成的Hj及所有声场测点处的Hj组成声压传递函数拷贝场,即:
(4)
当测点声压与该测点处的拷贝场相匹配时,声压与拷贝场的相位相同,因此,建立如下的目标函数:
(5)
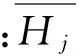
通过寻找目标函数FPj最接近零值时所对应的[δ1,δ2,…,δn],从而确定声场总传递函数Hj。
根据式(3)计算各力源强度Δi,从而确定力源工作状态及各力源强度,实现水下弹性结构力源识别。
2粒子群模拟退火融合算法基本原理
针对式(5)的目标函数极值进行搜索,实际上是一个非线性函数的极值优化问题。粒子群优化算法(Particle Swarm Optimization,PSO)是进化计算领域的一个分支,粒子群在追逐最优粒子的过程中,随着它越来越接近最优的粒子,其更新速度越来越小,因此,简单的粒子群算法容易陷入局部极值中。而模拟退火(Similated Annealing,SA)算法最主要的特征是具有跳出局部极值点区域的能力,能够找到全局最优或者是近似最优,与起始位置的选择无关。因此,本文选用了粒子群与模拟退火相融合的搜索算法进行激励力源强度的匹配搜索[11-12]。
这种基于模拟退火机制的粒子群搜索算法,其粒子的追踪过程相对独立,可以保证种群的多样性,而在每个相对独立的进程中引入了模拟退火算法以跳出粒子群局部极值。具体匹配搜索过程如下:
(1) 将各激励力源强度之间的比例系数[δ1,δ2,…,δn]看作粒子,因此,每一个粒子的维数与激励源个数相同。定义如下变量:
x:粒子当前位置;ϑx:粒子在当前位置处的适应度;xbest:每个粒子在当前迭代过程中最佳位置;ϑxbest:粒子在当前迭代过程中最佳位置上所对应的适应度;gbest:粒子在全局中的最佳位置;ϑgbest:全局最佳位置对应的适应度。
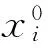
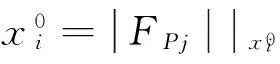
(6)
式中:i=1,2,…,M,M为粒子个数;FPj计算方法如式(5)。
(3) 令ϑxbest=min(ϑx0),ϑgbest=ϑxbest;
(4) 按下式更新粒子的位置及速度:
(7)
(8)
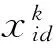
w=maxw-k*(maxw-minw)/N
(9)
式中:maxw:惯性权重的最大值;minw:惯性权重的最小值。
(5) 利用式(6)计算ϑxk,令ϑxbest=min(ϑxk);比较ϑxbest与ϑgbest,当ϑxbest<ϑgbest时,gbest=xbest,否则gbest不变。
(6) 针对每一个粒子,分别计算粒子位置、速度变化前后的适应度变化量Δϑ,计算如下的接收函数[21]
f=exp(-Δϑ/T)
(10)
式中:T为目前系统的温度。
如果f>rand(0,1),则接受变化后的新速度及新位置,否者不接受新产生的位置及速度。
(7) 判断是否达到指定的迭代次数或达到指定的适应度值:如果是,搜索过程结束,输出最优位置及相应的自适应度值;否则按照式(9)更新惯性权重,并按照下式更新系统温度:
T(k+1)=m*T(k)
(11)
式中:m为一个接近于1的常数,一般取值为0.5~0.99。
因此,按照式(11),该算法对于算法控制参数的衰减量是随着算法迭代次数递减的。
更新惯性权重与系统温度后,返回步骤(4),直到达到最大迭代次数,或是达到所要求的适应度值。
3数值仿真结果分析
为了验证这种粒子群模拟退火算法对结构噪声源识别的有效性,以具有多激励源的水下单层圆柱壳体作为物理模型,采用有限元法及边界元法,利用商业软件ANSYS及SYSNOISE进行了结构受力源激励下的辐射声场数值预报,建立广义声压传递函数拷贝场。
圆柱壳体模型内部为空气,外部为水介质,长1 m,半径0.08 m,壳体厚度:3 mm,壳体上下两端盖厚度为15 mm,两端为自由边界条件。壳体的材料参数杨氏模量E=2.06×1011N/m2,泊松比σ=0.3,密度ρ=7 800 kg/m3。流体密度ρ0=1 000 kg/m3,声速v= 1 500 m/s。模型长度方向划分为16份,圆周方向划分为16份。
取模型几何中心为坐标原点,长度方向为z轴。针对力源位于壳体不同位置处时的情况,分别计算力源至场点声压的传递函数,力源大小为1 N,方向径向向外。计算壳体外围一个半径为0.3 m,长1.5 m的圆柱形包络面上的辐射声压,建立声压传递函数拷贝场,进行力源匹配分析。将搜索算法的阈值条件记为tc,则算法的终止条件为:
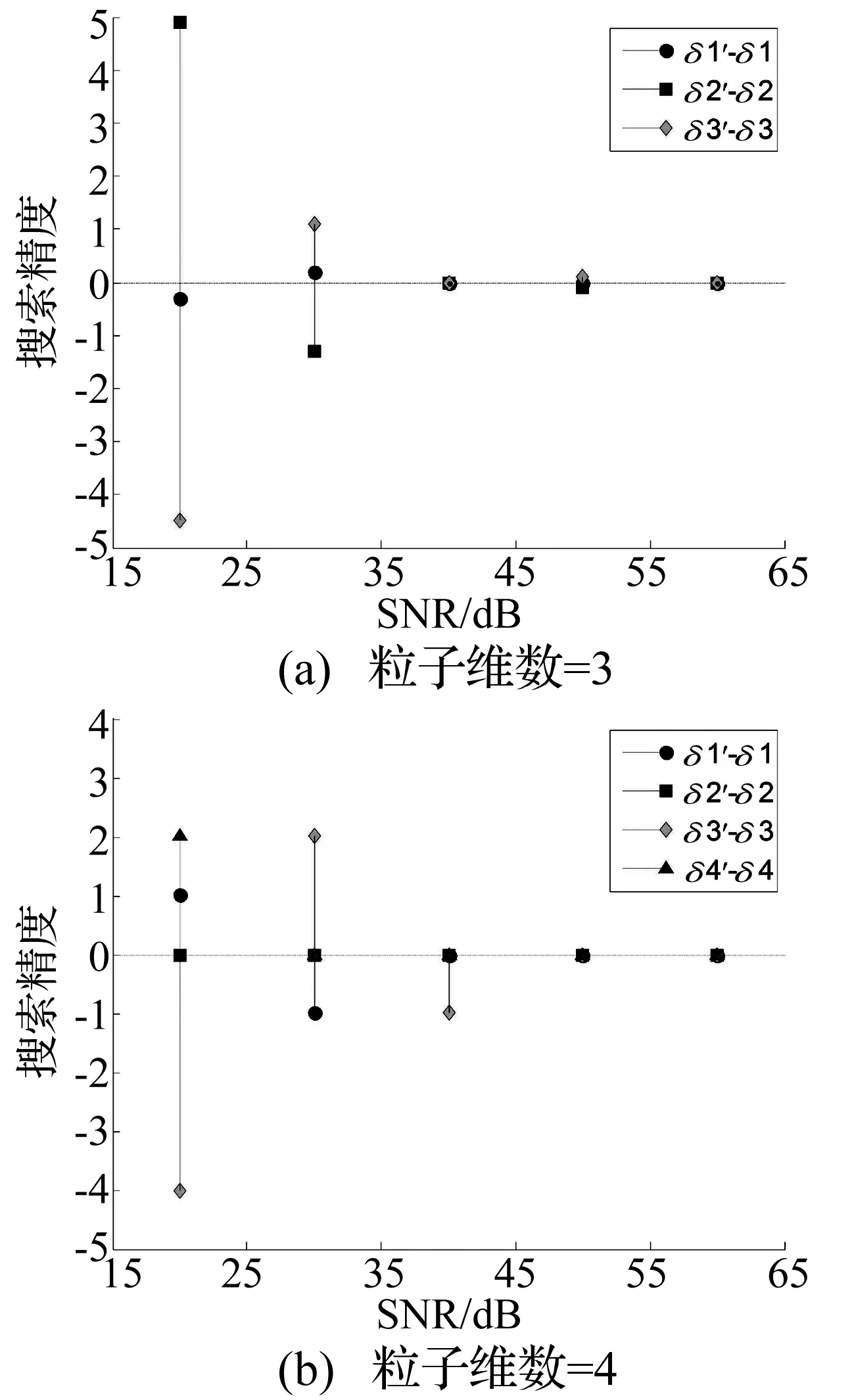
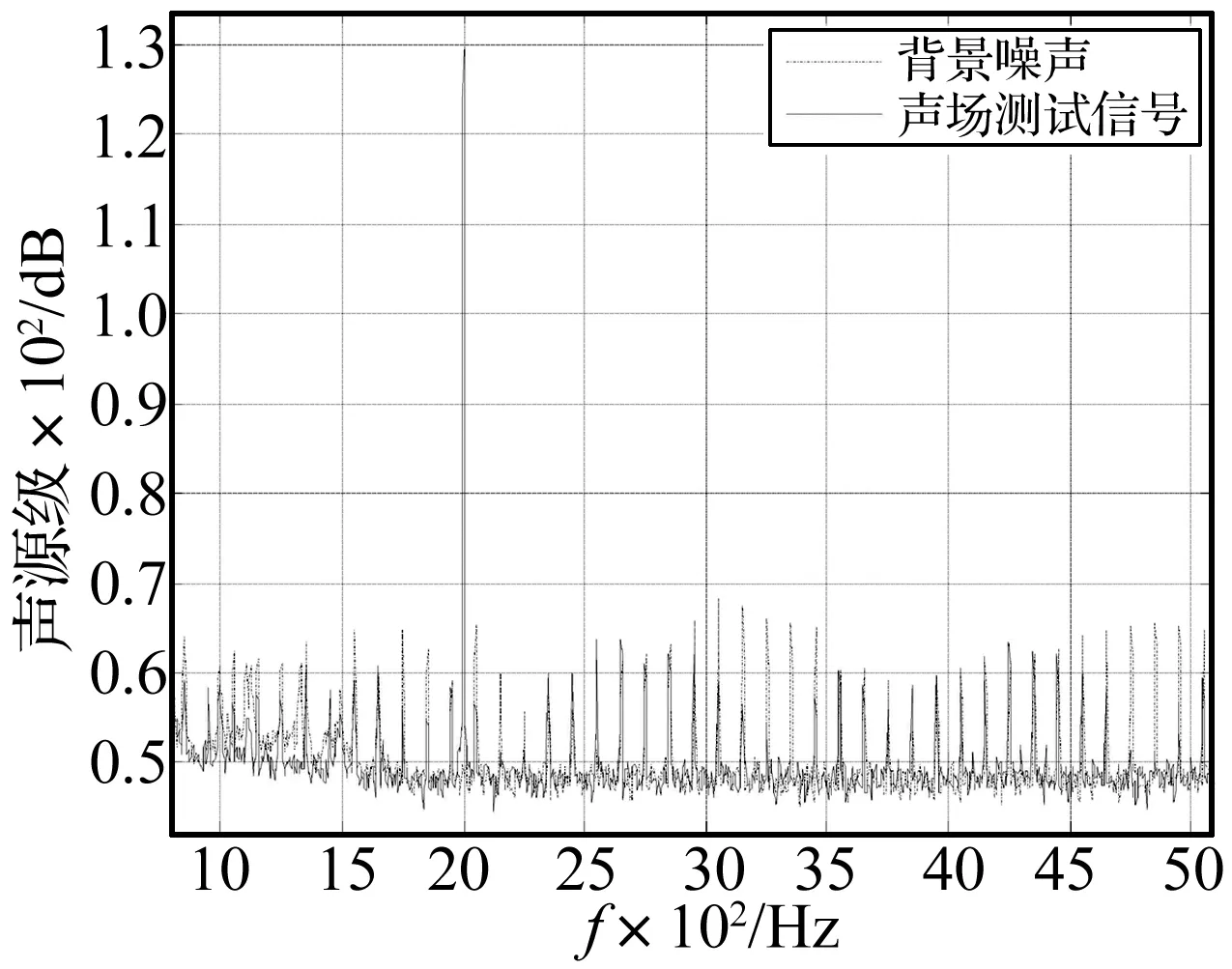
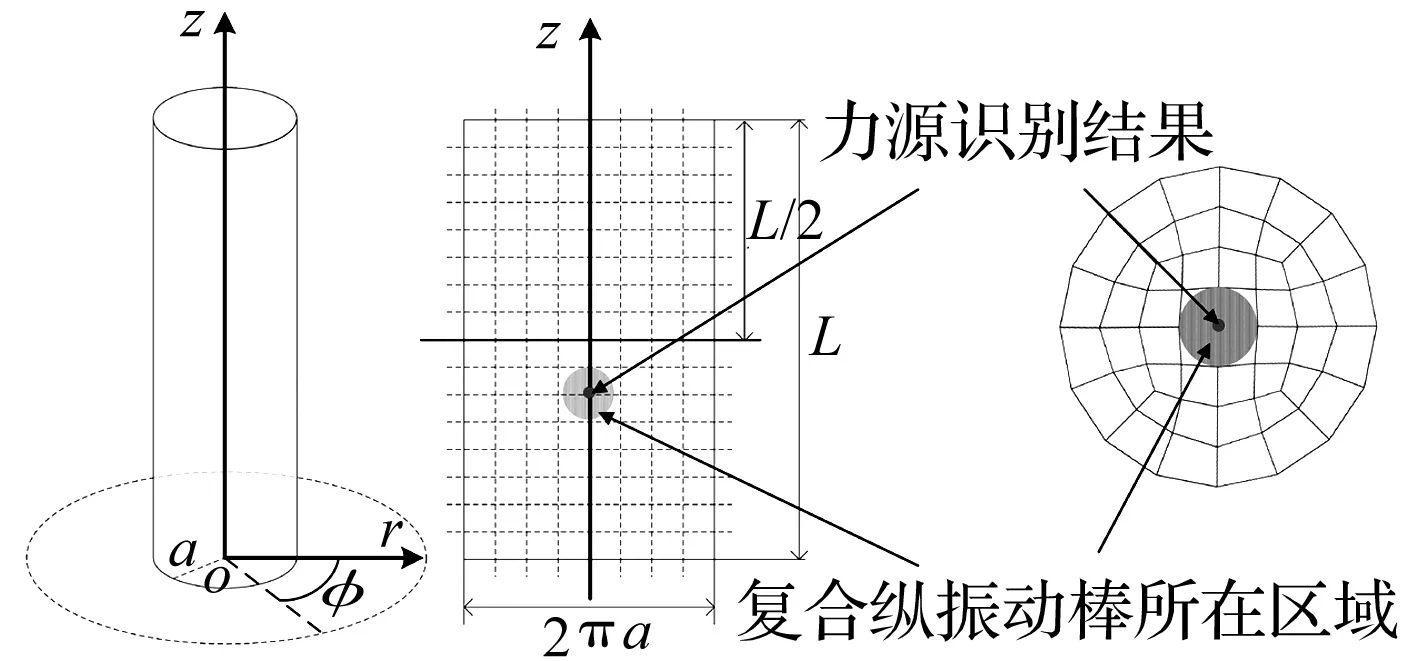
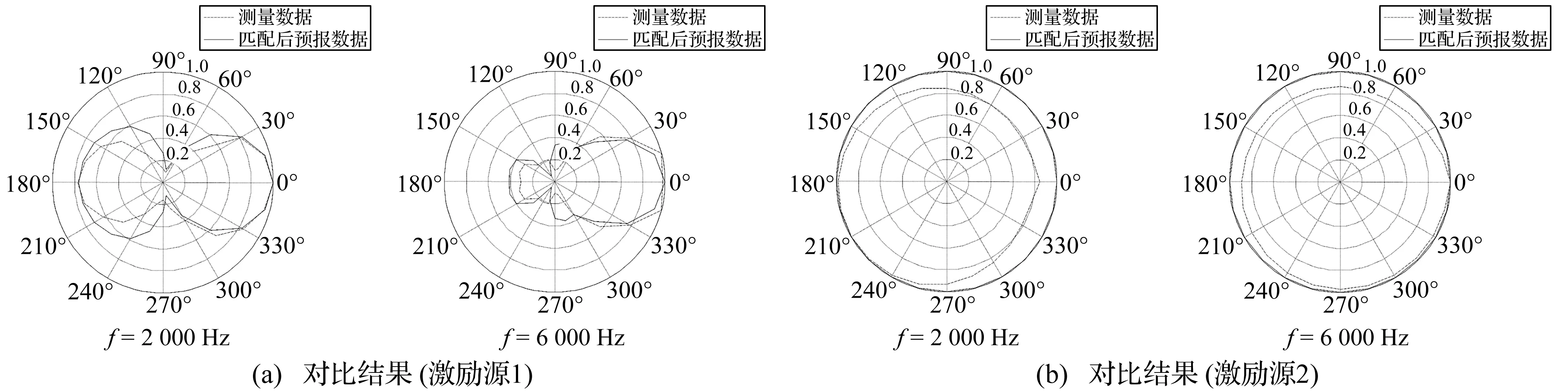
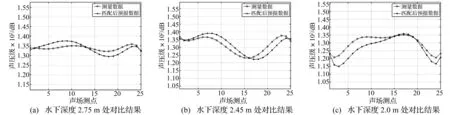
ϑgbest (12) 仿真条件如下: tc= 0.000 1°;M=10,N=800;c1=1.49,c2=1.49;maxw= 0.94,minw=0.4;T0=20,m=0.88。 假设壳体内部具有4个激励力源,力源强度分别标记为Δ1、Δ2、Δ3及Δ4。力源位置分别为:(0.08,0,0),(0.08,0,-0.25),(0.08,0,0.25),(-0.08,0,0.125)。针对不同力源组合形式进行了辐射声场数值仿真计算,将计算结果与建立的声压传递函数拷贝场进行匹配处理,分析力源位置和强度。针对具有非相干加性噪声干扰的情况进行了数值仿真分析,图2所示为不同信噪比情况下结构内部力源强度的搜索精度。 图2 不同粒子维数条件下的搜索精度Fig.2 The accuracy in different dimension conditions 从图2可知,采用这种粒子群模拟退火融合算法可以较为精确的搜索到每一个力源的比例系数,源强度识别结果的误差远小于1%。随着信噪比增加,识别精度也逐渐提高,当信噪比>40 dB时,搜索结果几乎与理论预设值相同。 在不同阈值条件下进行了算法精度与搜索效率的仿真分析,信噪比设定为40 dB。各力源强度的理论预设值分别为Δ1=0.25, Δ2=0.25, Δ3=0.10, Δ4=0.40,阈值条件tc:0.1°×10-2~0.1°×10-5。 分别进行了6次相同情况的数值仿真,图3为6次搜索结果的平均误差,从图3可知,随着算法的阈值条件越高(即tc越小),搜索精度不断提高。当tc≤0.1°×10-3时,搜索结果与理论值几乎一致。 图3 不同阈值条件下的搜索精度Fig.3 The accuracy in different threshold value conditions 图4为6次仿真所用的搜索时间,从图4可知,tc越小,所用的搜索时间越长。而且,当tc≤0.1°×10-3后,几次搜索所用时间趋于稳定。因此,针对本文的仿真模型以及拷贝场容量,阈值可以选为tc=0.1°×10-3。 图4 不同阈值条件下的搜索时间Fig.4 The searing times in different threshold value conditions 4试验数据分析 为了验证本文提出的水下结构激励力源匹配场识别处理方法在实际应用中的可行性,在消声水池中进行了水下圆柱壳体结构振动及声辐射测试试验。试验模型与数值仿真模型相同,为一个单层圆柱壳体模型,模型长1 m,半径为0.08 m。内部安装有两个复合纵振动棒作为激励力源。 图5 圆柱壳模型及内部复合棒换能器实物图Fig.5 The photographs of cylindrical shell model and internal composite rod transducer 在壳体内部靠近激励力源的位置各放置一个加速度计,将壳体安装在消声水池回转机构上,竖直放入水下,模型几何中心位于水面下2 m处。水听器阵由12个水听器组成,相邻水听器间距为0.15 m,阵长1.65 m。水听器阵竖直放入水中,距离模型几何中心0.5 m,最上端的水听器距离水面1.25 m。具体位置见图6。 图6 试验模型及声场测点示意图Fig.6 The scheme of the exciting force inside the shell 使用信号发生系统中两个信号源通道对两个激励源进行分别控制,两个激励信号经由相同型号的功率放大器,试验时保证功率放大器放大倍数一致。利用消声水池的回转机构旋转壳体,每次旋转15°,共旋转24次,实现距离圆柱壳体50 cm及1 m处的一周辐射声场测量及结构振动测试。 4.1单点力源激励情况 以结构受力源激励产生的辐射声场作为匹配分析物理量,根据实际壳体模型结构建立辐射声压传递函数拷贝场,选择壳体内部激励源附近的加速度计作为参考加速度计,计算各辐射声压测点处接收信号的相对值,采用数值方法计算相应的传递函数拷贝场,并进行相关匹配处理。对接收系统中各通道的信噪比进行了分析,均>30 dB,图7为水下2.75 m处水听器接收信号的信噪比。 图7 辐射声压测量结果信噪比(f=2 000 Hz)Fig.7 The SNR of the radiation pressure measurement results (f=2 000 Hz) 针对仅有一个激励源工作的情况,进行力源位置识别。取模型几何中心为坐标原点,长度方向为z轴。针对力源位于壳体不同位置处时的情况,采用有限元与边界元的方法分别计算力源至场点声压的传递函数,力源大小为1 N,方向径向向外。分析所有测点位置处的辐射声压,当仅有一个力源激励时,仅需要对其位置进行分析,不需要分析权值,仅需要考察每一个位置处激励力源至辐射声场的传递函数与实际测试声场的相位匹配情况即可。只分析相位时,拷贝场的容量有限,因此,可以采用精度最高的枚举法进行匹配搜索,对两个力源分别进行位置识别,具体结果见图8。 图8 单点力源激励情况下力源位置识别结果(f=2 000 Hz)Fig.8 The identification results of exciting force source location(f=2 000 Hz) 从图8可知,力源识别结果与实际位置相吻合。采用力源位置的识别结果,对结构的辐射声场进行预报,考察1m处辐射声压幅值。由于仅对相位进行匹配搜索,并没有对力源的权值进行分析,因此对一周24个点上的幅值进行归一化处理,与实际测量结果进行对比,对比结果见图9。 从图9可知,采用力源位置的识别结果进行辐射声场预报时,与实际测量结果较为接近。这种利用实际测量值与传递函数相位进行匹配搜索的力源识别方法是可行的。 图9 辐射声压测量结果与预报结果对比Fig.9 The comparison of radiation pressure measurement results and forecasted results 4.2两个力源共同激励情况 在对力源的位置分别进行识别以后,针对两个力源共同激励的情况,利用水听器测量接收得到的辐射声压进行力源强度匹配搜索。利用两个噪声源单独激励时的辐射声场与壳体振动试验数据,建立各源与辐射声场之间的传递函数。采用粒子群模拟退火算法进行力源强度匹配搜索。粒子群中粒子个数M=10,最大迭代次数N=500,算法阈值条件tc=0.01°。其他参数与数值仿真分析时相同。利用匹配后得到的声源强度比例系数结合声压传递函数,对壳体结构受力源激励产生的辐射声场进行了预报。取不同深度上一周25个测点出的辐射声压预报结果与实际测量结果进行对比分析,两个力源强度比例为1∶4时,对比结果见图10。 从图10可知,圆柱壳体受力源激励而产生的辐射声场的预报结果与实际测量结果整体趋势吻合较好,平均误差小于5 dB,但是个别测点处的辐射声场预报误差较大。因此,对结构的辐射声功率进行预报,并与实际测量结果进行对比分析。 从图11可知,在2 000~10 000 Hz的频带内,模型的辐射声功率预报结果与实际测量结果吻合良好。即:采用粒子群模拟退火融合算法的力源强度搜索结果与实际力源的强度较为接近。利用识别结果可以很好的对结构振动产生的辐射声功率进行预报分析,相对而言,对于某一固定位置处的辐射声压预报结果误差较大。需要说明的是,从单点力源的识别结果中可以发现,声场预报结果与实际测量结果虽然较为接近,但仍有一定的误差。因此,本文中对试验数据进行匹配搜索时,采用的是每个力源单独激励时的辐射声场测试结果作为拷贝场。如果采用数值仿真计算结果作为拷贝场,则要求较高的结构振动及辐射声场数值预报精度,需要开展适用于大尺度水下复杂结构的振动及辐射噪声快速预报方法研究[13],这也将是水下力源识别匹配处理方法的主要研究内容之一。 图10 f=2 000 Hz时的对比结果Fig.10 The comparison results at the condition that f=2 000 Hz 图11 辐射声功率对比结果Fig.11 The comparison results of the sound power 5结论 本文提出了一种水下弹性结构力源识别的匹配场处理方法,这种方法将实际测量的声场与模型预测声场进行相关匹配处理,从而确定力源位置、贡献量等信息。文中尝试采用力源识别粒子群模拟退火融合搜索方法进行传递函数匹配搜索,针对单层圆柱壳体进行了力源识别匹配处理数值仿真分析以及试验数据处理分析。仿真结果及试验结果均表明:在信噪比达到要求时,采用这种方法可以较好的实现激励力源强度识别。而且将识别后的结果应用于结构辐射噪声预报时,预报精度很高。同时,采用这种方法对测试距离没有固定要求,因此声场布放的形式相对较为灵活,将具有很好的应用前景。 [1] Chakravorty P K.Identification of self noise sources in a ship[J].Naval Engineers Journal, 1990, 102:67-69. [2] 蒋国建,任克明,马杰,等.噪声抵消法估计和抑制声呐部位主要自噪声[J]. 声学学报,1996,21(4):289-296. JIANG Guo-jian, REN Ke-ming, MA Jie, et.al. Estimation and rejecting the main self-noise of sonar-position by noise cancelling method[J]. Acta Acustica, 1996,21(4):289-296. [3] 董建超,杨铁军,李新辉,等.主分量分析在激励源识别中的应用研究[J].振动与冲击,2013, 32(24):157-163. DONG Jian-chao,YANG Tie-jun,LI Xin-hui,et al. Applications of principal component analysis in excitation source identification[J]. Journal of Vibration and Shock, 2013, 32(24):157-163. [4] 时胜国,杨德森. 水下声强测量分析系统及其在近场测量中的应用[J]. 测试技术学报,2002,16:475-480. SHI Sheng-guo, YANG De-sen. An underwater sound intensity measurement system and its application to its radiation noise measurement of underwater structure in the near-field[J]. Journal of Test and Measurement Technology,2002,16:475-480. [5] 陈梦英,商德江,李琪,等.运动声源的边界元声全息识别方法研究[J]. 声学学报,2011,31(5): 489-495. CHEN Meng-ying, SHANG De-jiang, LI Qi, et al.Nearfield acoustic holography based on inverse boundary element method for moving sound source identification[J]. Acta Acustica, 2011,31(5): 489-495. [6] Baggeroer A B, Kuperman W A. An overview of matched field methods in ocean acoustics[C]//IEEE Journal of Oceanic Enigeeing, 1993,18:425-427. [7] Tolstoy A, Horoshenkov K V, Bin Ali M T. Detecting pipe changes via acoustic matched field processing[J]. Applied Acoustics, 2009, 70: 695-702. [8] 董姝敏,刘洪波,赵博,等.匹配场声源定位的并行计算方法研究[J]. 计算机应用研究,2012,29(2):514-517. DONG Shu-min, LIU Hong-bo, ZHAO bo, et al.Study on method of parallel computing in match field localization[J]. Application Research of Computers, 2012,29(2):514-517. [9] Xiao Yan, Shang De-jiang. Identification method for exciting force source inside underwater structure based on PSO_GA[J]. Journal of Ship Mechanics,2015, 19(3): 311-321. [10] Fahy F J. Sound and structural vibration: Radiation, transmission and response[M]. Amsterdam Boston Elsevier Academin, 2007. [11] 王振树, 李林川, 李波. 基于粒子群与模拟退火相结合的无功优化算法[J]. 山东大学学报:工学版,2008,38(6):15-20. WANG Zhen-shu, LI Lin-chuan, LI Bo.Reactive power optimization based on particle swarm optimization and simulated annealing cooperative algorithm[J]. Journal of Shandong University:Engineering Science, 2008,38(6):15-20. [12] 王华秋, 曹长修. 基于模拟退火的并行粒子群优化研究[J].控制与决策,2005,20(5):500-504. WANG Hua-qiu,CAO Chang-xiu. Parallel particle swarm optimization based on simulated annealing[J]. Control and Decision, 2005,20(5):500-504. [13] 吴绍维, 向阳, 夏雪宝. 基于无单元声波叠加的自辐射近似解析表达研究[J].振动与冲击,2014, 33(7):79-85. WU Shao-wei, XIANG Yang, XIA Xue-bao. Approximate analytical expressions of self-radiation terms inclading acoustic pressure and velocity based on element free acoustic wave superposition[J]. Journal of Vibration and Shock, 2014, 33(7):79-85. Application of PSO-SA algorithm in underwater structure exciting force source identification XIAO Yan1,2, SHANG De-jiang1,2 (1. Acoustic Science and Technology Laboratory, Harbin Engineering University, Harbin 150001, China;2. College of Underwater Acoustic Engineering, Harbin Engineering University, Harbin 150001, China) An identification method by MFP is proposed for exciting the force source inside an underwater structure, and a concept of generalized copy field based on the structural acoustic radiation field is established. The particle-swarm optimization-simulated annealing (PSO-SA) algorithm is adopted for searching the optimum force source strengths. A single cylindrical shell in an underwater free field is selected as the investigated subject, and the sound radiation transfer function copy field is numerically calculated. The matched searching algorithm is simulated. The vibration and radiation sound pressures of the actual single cylindrical shell are measured in the anechoic tank. The measurement result and the numerical copy field are matching processed to search the optimum source strength. Both the simulation and the experiment results show that this method is effective for analyzing the source intensity. Moreover, the forecast accuracy is high when using the source-matching identification results to predict the radiation sound pressures. underwater structure; force source strength; matched field processing; PSO-SA 10.13465/j.cnki.jvs.2016.12.036 国家自然科学基金(11274080) 2015-01-30修改稿收到日期:2015-06-24 肖妍 女,博士,讲师,1984年生 商德江 男,博士后,教授,博士生导师,1969年生 TH212;TH213.3 A