基于相空间独立分量分析及峭度贡献系数的早期故障分析方法研究

陈建国 ， 王　珍， 李宏坤

(1.大连大学 机械工程学院，辽宁　大连　116622; 2.大连理工大学 振动工程研究所，辽宁　大连　116023)

基于相空间独立分量分析及峭度贡献系数的早期故障分析方法研究

陈建国1， 王珍1， 李宏坤2

(1.大连大学 机械工程学院，辽宁大连116622; 2.大连理工大学 振动工程研究所，辽宁大连116023)

独立分量分析方法在信号分析中具有振源分离的特点,但由于机械设备早期故障信号具有强背景噪声及振源复杂等特点，独立分量分析方法对于单通道强背景噪声信号中的早期故障检测也无法取得满意效果。因此提出相空间对独立分量方法对其进行振源分离及重构，获得早期故障成分较为集中的重构信号，进而提出了峭度贡献系数来提取重构信号的早期故障特征信息;在对于某挤压机变速箱轴承的早期故障信号应用中，此方法在强背景噪声下成功的提取了早期故障的特征信息,确定了早期故障发生的部件。上述实验证明，相空间独立分量分析及峭度贡献系数方法在早期故障检测方面提供了一个可行的研究方向。

相空间独立分量分析；峭度；峭度贡献系数；早期故障

弱信号检测技术一直是国内外学者研究的重点之一，而现代机组工作时复杂的结构、高环境强噪声干扰、机组间的振动耦合、机组结构滤波和传感器拾取信号杂乱等问题使弱信号识别方法一直为振动信号分析的难点之一。随着信号分析技术的发展，具有盲源分析能力的独立分量分析(Independent Component Analysis，ICA)在机械振动信号分析领域得到推广研究。Blanco等[1]验证了ICA能够实现信号振源的辨识和信号信息冗余的消除，从而有利于早期信号的提取。宋友等[2]利用ICA实现了早期碰磨试验台微弱信号中的故障检测，Gruber等[3]利用Local ICA实现了含噪声环境下早期微弱信号的提取。上述ICA研究的信号都基于试验台和多通道的特点，但工程实际信号的强环境噪声及单通道拾取信号等特点限制了ICA的深化应用，所以本文提出相空间ICA方法和峭度贡献系数指标实现单通道工程振动信号中微弱故障信号成分的有效检测。

1独立分量分析原理

标准ICA的数学模型为

x=As

(1)

式中：x=(x1,x2,…,xN)T为多元随机混合信号，即观测信号，A为N×N常数混合矩阵，s=(s1,s2,L,sN)T为分量彼此统计独立的信号源[4]。ICA可以在仅知观测信号x的情况下，获得N×N解混矩阵W=(w1,w2,L,wN)T，进而得：

u=Wx

(2)

式中：u=(u1,u2,…,uN)T为在观测信号中分离得到的估计源信号。为了确保ICA模型能够被准确估计，作出了三个假设和约束：① 每个信号源被假定是统计独立的；② 每个信号源必须具有非高斯分布；③ 假定信号源数目小于观测信号的数目。这些假设和约束限制了ICA方法的应用[5]。

2相空间ICA原理

利用ICA完全提取早期信号需要明确以下条件：机械内部振源的数目；安放传感器的数目要大于等于振源数目；安放传感器的位置要尽量接近振源产生的部位。工程信号大多是强环境噪声的若干振源的单通道信号，无法满足上述严格的条件，所以ICA对于工程信号中的微弱信号成分无法准确分离。针对此现象，本文利用单通道加速度信号进行相空间重构的方法，ICA对重构的相空间信号进行盲源分离[6]，获取不同空间中的信号成分，用以辨别微弱信号成分信息。

相空间ICA方法的流程见图1，相空间ICA的详细步骤为：① 对单维轴承故障信号进行延时相位重构，获取m维N列的原故障信号空间。② 从而进行ICA方法分析获取m个估计振源信号和分离矩阵W。③ 对估计信号按峭度指标进行聚类，分为微弱冲击信号和无冲击信号，求分离矩阵的逆矩阵A=W-1并使对应于无冲击信号对应值为零，重构一个完全由冲击信号组成的信号。④ 对于微弱冲击成分，本文后续提出峭度贡献系数概念并用其辨识早期故障特征信息。

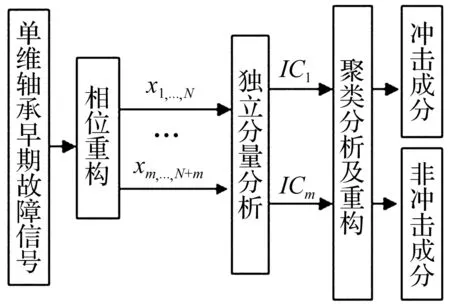
图1　相空间ICA方法流程图Fig.1 The flow chart of phase space ICA

3峭度贡献系数

峭度是振动幅值概率密度函数陡峭程度的量度。它对于信号中的冲击成分特别敏感，是判断冲击故障的主要参数之一[7]。但对于强噪声工程信号，峭度值无法辨识强噪声中微弱冲击成分。为了更加准确的表征微弱冲击信号成分，本文提出了峭度贡献系数的概念。其具体物理意义为：

对于X=x1,x2,…,xN，在本文定义峭度为：

(3)

因为标准正态分布的标准峭度值3，而具有冲击故障信号为非标准正态分布，其标准峭度值>3，所以式(3)定义的峭度值为标准峭度值减3，当式(3)峭度值为正数则预示故障的产生。峭度是整个序列中每个数据点的整体统计量，如果衡量x1,x2,…,xN中某一点xi对整个序列峭度的贡献，则可以考虑整个序列除去此点之后峭度发生的变化。从而，某点的峭度贡献系数定义为用完整序列的峭度和缺少此点序列的峭度差值的绝对值来衡量，其计算式见式(4)～式(5)：

(4)

(5)

式中：Kurt(xj=1,2,…，N,j≠i)为缺少xi点时N-1个序列的峭度值。Kurt(xi)为xi点对整体峭度的贡献系数。

4峭度贡献系数仿真

下面以一组仿真周期冲击信号来查看峭度贡献系数的表征度。冲击信号按照下式构成[8]：

X=e-akt×sin(2πfckT)

(6)

式中：a=1 000,k=2 048,fc=5 000,T=1/25 000,fm=50，t=mod(k×T,1/fm)；mod(·)为matlab中求余数运算。按式(6)得到冲击信号和按式(5)求取每个冲击信号每个点峭度贡献系数见图2。

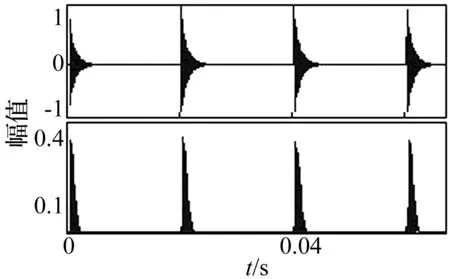
图2　冲击信号及各点峭度贡献系数Fig.2 The transient impulse signal and contribution coefficient of kurtosis

从图2可知，峭度贡献系数曲线和冲击信号一一对应，能够很好的表征冲击信号的位置和周期特性。但工程信号中常常遇到的是微弱冲击信号隐没于环境噪声中，较难精确的找出其周期性。所以下面在冲击信号中加入噪声信号，验证峭度贡献系数表征冲击的能力。

图3、图4分别为信噪比SNR=2.663、SNR=1.105时冲击信号的时域波形和其各点的峭度贡献系数。由图可知峭度贡献系数对于噪声具有一定的免疫能力，能清楚的表征冲击信号的位置和周期，具有一定的工程实用价值。

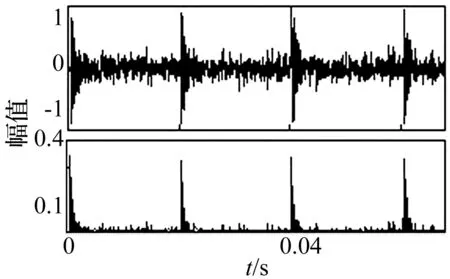
图3　SNR=2.663时峭度贡献系数Fig.3 Contribution coefficient of kurtosis with SNR=2.663

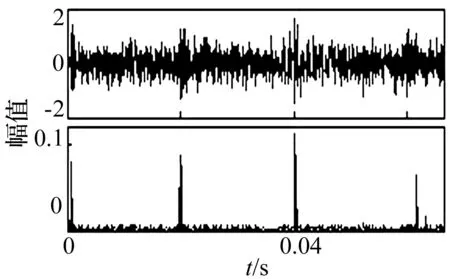
图4　SNR=1.105时峭度贡献系数Fig.4 Contribution coefficient of kurtosis with SNR=1.105

5相空间ICA在轴承早期故障的应用

工程信号为某石化厂挤压机组齿轮箱中的轴承工程信号，经过对信号的跟踪获某一轴承的早期、中期和后期的故障信号。本文对其早期故障信号进行分析，轴承故障部位为轴承内环，其特征频率为68.75 Hz，变速箱的齿轮啮合频率为387.5 Hz。

早期轴承故障时域波形与频域波形见图5。从时域图上无法看出其冲击成分，在频域图形上出现了比较明显的几个频率成分，50 Hz是工频干扰，387.5 Hz、1 163 Hz、1 944 Hz是啮合频率的倍频成分，但是没有出现内环的故障频率，在高频带的也看不到共振频带。并且运用EMD和小波方法进行了分析，也无法提取内环故障信息，由于篇幅原因不再进行详细论述。

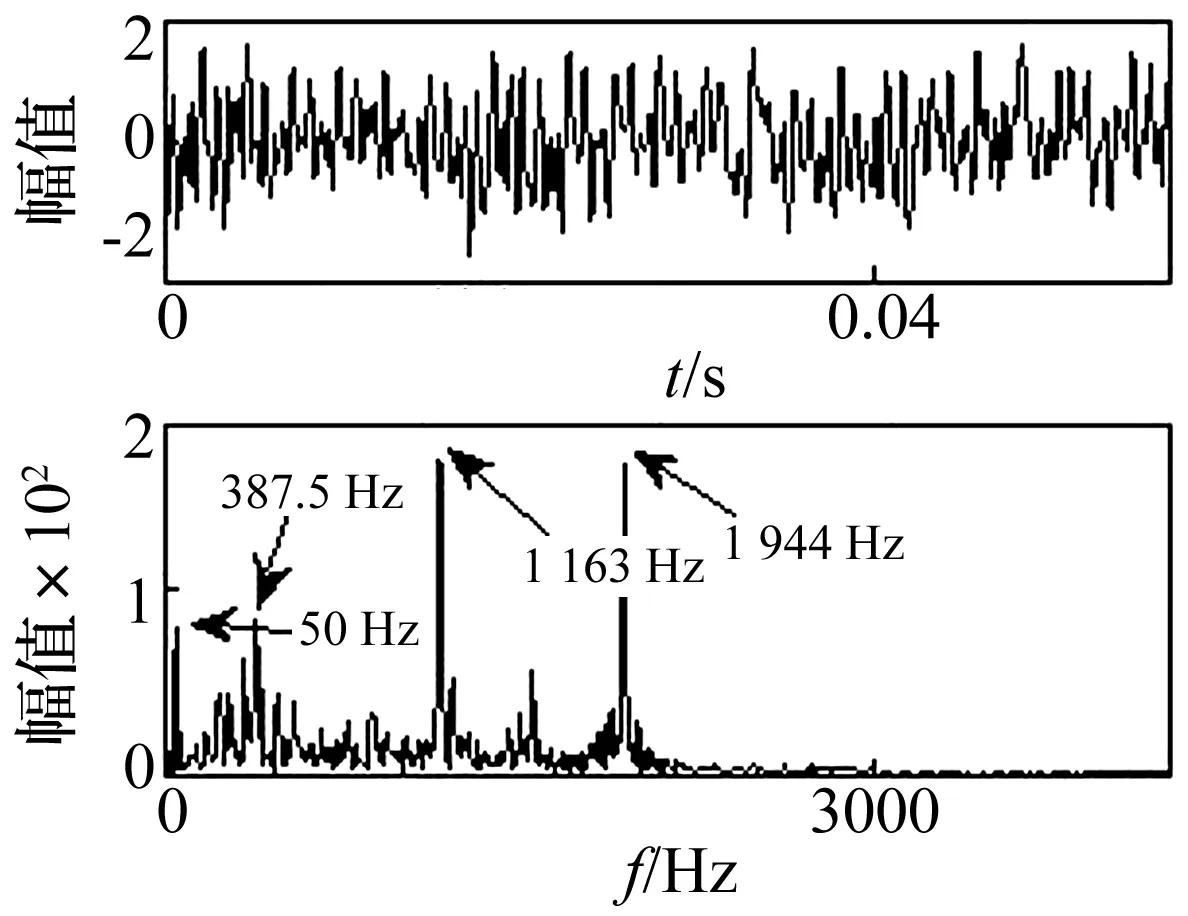
图5　轴承早期故障时域和频域波形Fig.5 The time and frequency spectrum of bearing incipient fault

下面利用本文提出的相空间重构ICA方法对轴承早期故障信号进行分析。首先运用Fraser和Swinney交互信息[9]求延迟时间方法确定其相空间重构的时间延迟为1，运用Cao方法[10]确定相空间重构的嵌入维数为10。

对轴承早期故障信号进行延迟时间为1、嵌入位数为10的相空间重构，把获取相空间内10维的数据作为ICA的输入数据，对这10维数据进行信息冗余消除，获取较好独立性的估计信号的时域频域谱见图6。

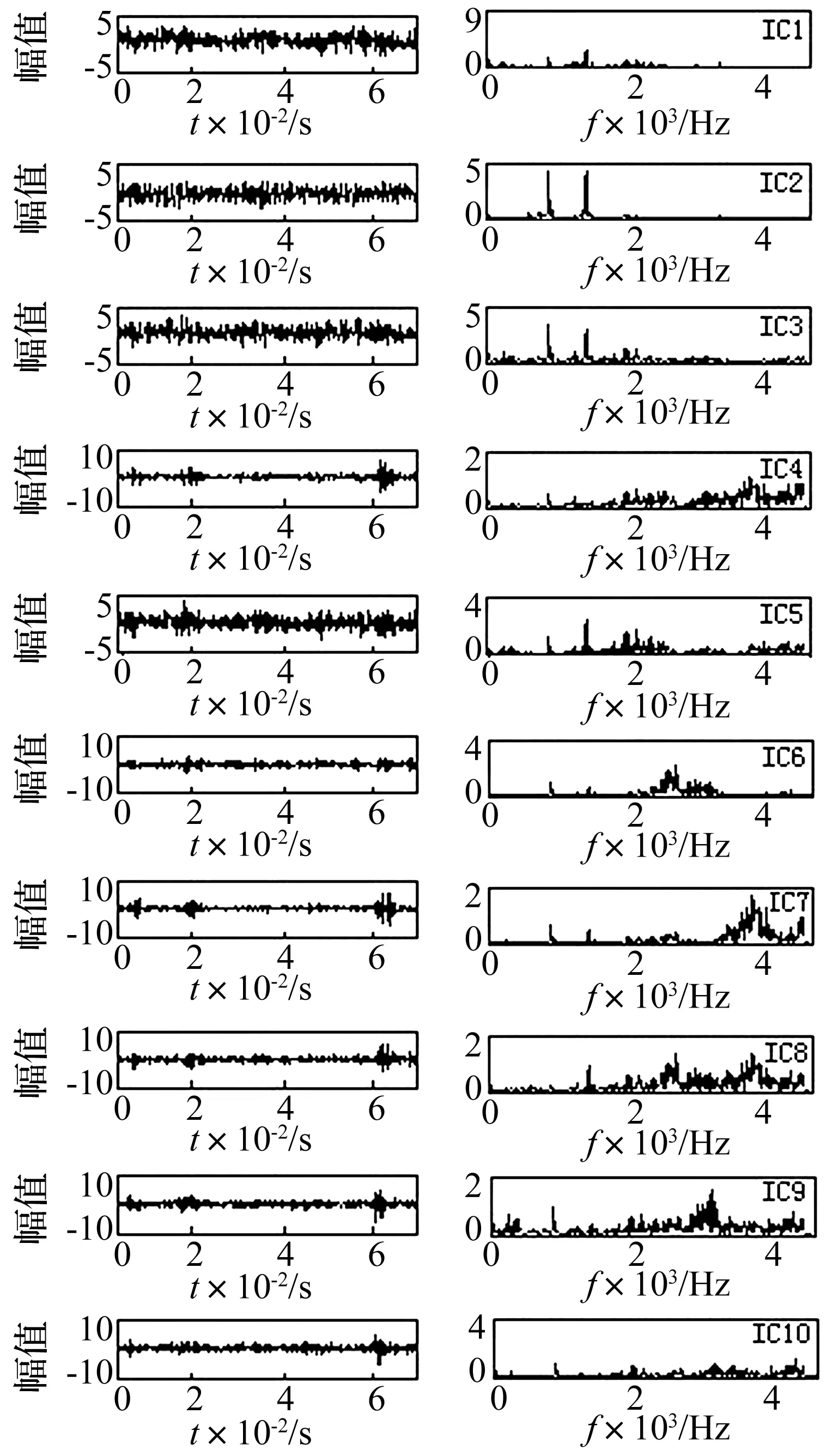
图6　ICA分离相空间信号得到的估计信号Fig.6 Estimated signal separated by ICA

由图6的时域谱可知，分离所得的很多信号中出现了较为明显的冲击成分，在频域谱可以看到多个微弱的冲击频谱。为了更加准确的提取轴承内环早期故障产生的冲击信息，对ICA分离的估计信号进一步的进行简单的聚类分析。计算相空间ICA分离出的10维信号的峭度值见表1。

表1　 相空间ICA分离信号的峭度

由表1可以看出第4、第7、第8、第9、第10个估计信号的峭度值很大，其时域谱内冲击信号较为明显。所以上述估计信号相加组合为一个冲击较为明显的重构信号见图7。但是必须注意，经相位空间ICA方法分离独立分量间仍然保持着时移特性，要进行互相关分析进行反向时移，弥补时移对冲击群峰带来的扩散影响。由图7可知,几个比较明显的冲击，但是早期故障信号中冲击成分幅值较小，并且每个冲击信号的幅值具有很大的差异，所以也很难得到重构信号的冲击成分特征信息。

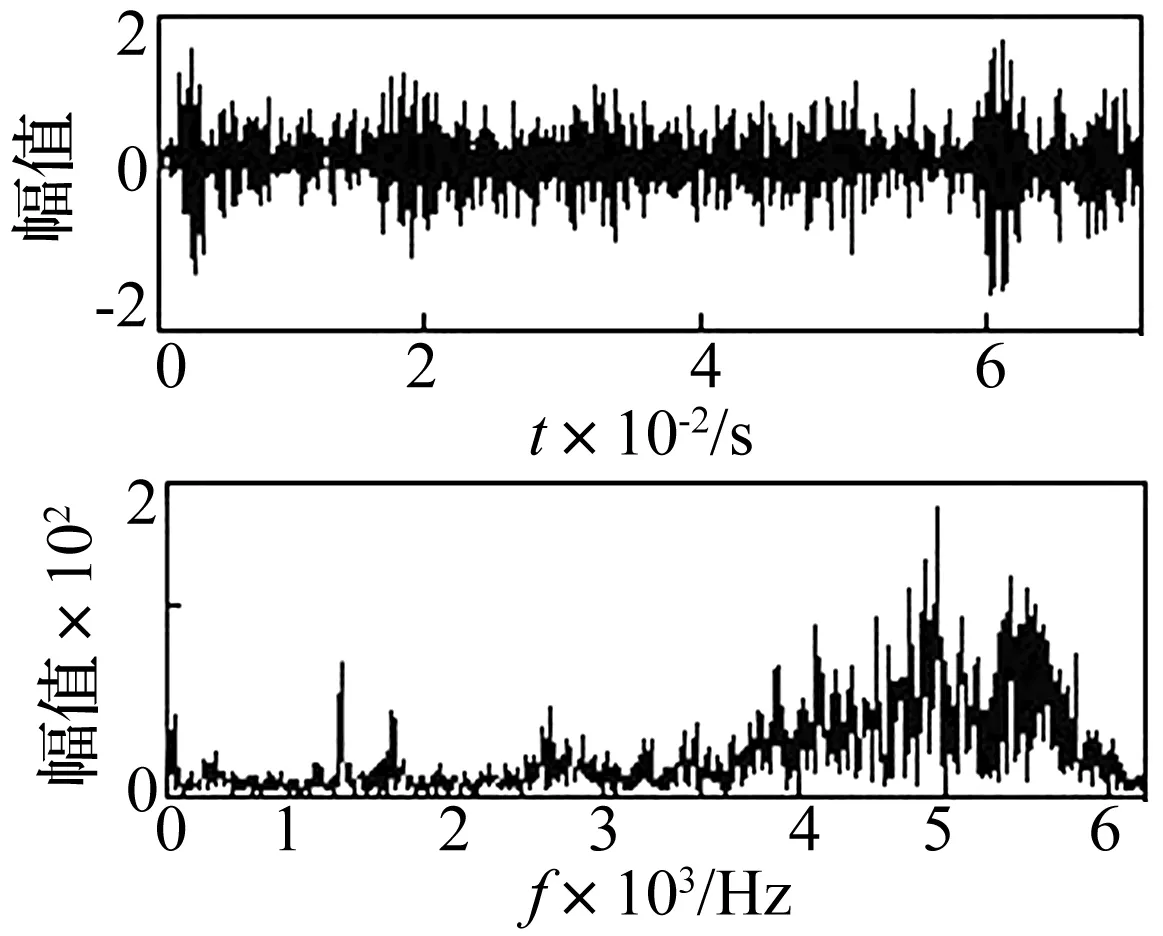
图7　冲击成分重构信号的时域频域波形Fig.7 Time and frequency waveform of reconstructed signal by impulse

为了准确的判断出冲击信号的周期，从而求取特征频率，确定轴承的哪个部件发生故障，利用峭度贡献系数对重构信号进行分析。利用式(5)求由冲击成分重构的信号中每个信号单点的峭度贡献系数见图8。

图8　峭度贡献系数曲线Fig.8 The contribution coefficient waveform of kurtosis

由图8可知，在信号中出现了5次比较明显的冲击，并且第5此冲击能量很大，其它冲击能量较小，从而造成了五个冲击的峭度贡献系数幅值差异很大，并且冲击周期间出现了一些峭度贡献系数奇异点以及峭度贡献系数峰值不太集中的现象。所以对图8的峭度贡献系数曲线进行阈值伸缩调整。为了使得每个冲击的峭度贡献系数近似相等及减小奇异点的影响，设定一个最大阈值，对超出此阈值的峭度贡献系数利用调整权重系数进行缩小操作；为了使得峭度贡献系数的峰值谱线更加集中，设定一个最小阈值，对小于此阈值的峭度贡献系数利用调整权重系数进行缩小操作，使得峭度贡献系数曲线峰值谱线减少。根据图8的五个冲击的峭度贡献系数值，确定最大阈值为0.04，最小阈值为0.018；确定调整权重系数选取为0.25、1、0.3，从而使得各个冲击的峭度贡献系数更加清晰明了。按照式(7)对其进行伸缩调整，得到根据阈值调整后的峭度贡献系数见图9。

(7)

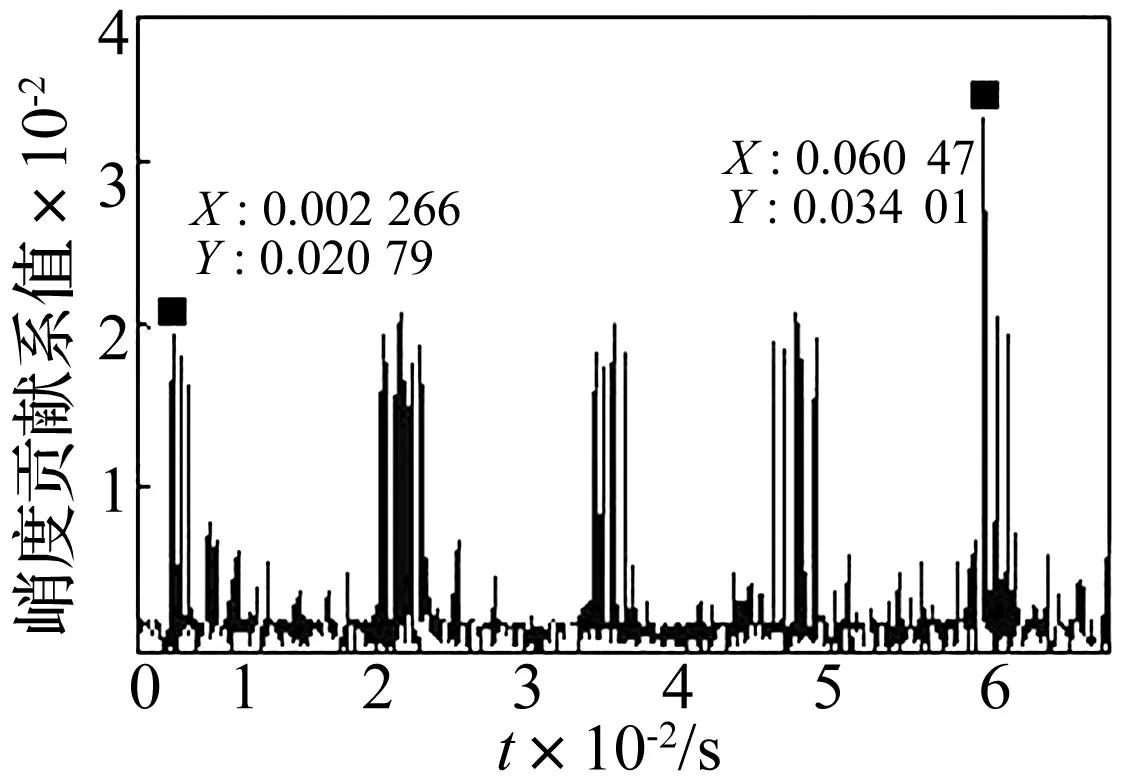
图9　调整后的峭度贡献系数曲线Fig.9 The adjusted contribution coefficient waveform of kurtosis

根据图9所示，调整后的峭度贡献系数具有明显的周期性，并且起始点也比较明确，第1个冲击成分开始的时间为0.002 266 s，第5个冲击成分开始的时间为0.060 47 s,由第1个冲击和第5个冲击的时间为0.058 204 s，共有4个冲击周期，故每个冲击周期平均为0.014 551 s,其冲击特征频率为68.724 Hz。上述得出的特征频率十分接近轴承内环的68.75 Hz的频率，所以可以确定图9中的冲击成分是由轴承内环早期故障所引起的。

由上述轴承内环早期故障信号分析结果得知，相空间ICA可以很好的提取轴承内环所引起的冲击成分，并可以用峭度贡献系数精确的确定冲击特征频率。所以相空间ICA在轴承早期故障中提取冲击特征信息具有很好的性能。

6结论

对于机械设备常见的单通道工程信号中早期故障成分难以有效检测和提取的问题，本文提出了相空间ICA方法及峭度贡献系数相结合的方法。通过对于挤压机变速箱的轴承单通道早期故障信号进行了验证，准确提取了轴承早期微弱冲击信号的周期及频率，从而准确判定了轴承的内环发生了早期故障。结果证明了相空间ICA及峭度贡献系数方法对于工程信号中的早期故障成分，特别是微弱冲击故障成分有很好的性能，为早期故障的诊断提供了一个有效的思路。由于峭度贡献系数是一个新的概念所以在后续需开展多点及奇异点的深入研究探讨，使其能够成为判断故障的一个常用信息量。

[1] Blanco D, Mulgrew B, Ruiz D P,et al. Independent component analysis in signals with multiplicative noise using fourth-order statistics[J].Signal Processing,2007,87: 1917-1932．

[2] 宋友，柳重堪，李其汉. 含噪振动信号中早期碰摩的故障检测研究[J]. 航空学报，2003, 24(1):32-35．

SONG You, LIU Zhong-kan, LI Qi-han. Early rub-impact fault detection in noise circumstances[J]. Acta Aeronautica et Astronautica Sinica, 2003, 24(1):32-35．

[3] Gruber P, Stadlthanner K,Bohm M, et al.. Denoising using local projective subspace methods[J]. Neurocomputing,2006,69: 485-497.

[4] Giri D, Rajendra Acharya U, Martis R J, et al. Automated diagnosis of coronary artery disease affected patients using LDA, PCA, ICA and discrete wavelet transform[J]. Knowledge-Based Systems, 2013,37:274-282．

[5] David L,Joseph M. Using the correlation dimension for vibration fault diagnosis of rolling element bearings—Ⅰ. Basic concepts [J]. Mechanical Systems &Signal Processing, 1996, 5: 241-250．

[6] Takens F. Dynamical system and turbulence, lecture notes in mathematics[M]. Berlin, Germany: Springer, 1981．

[7] 吴小涛， 杨锰， 袁晓辉，等. 基于峭度准则EEMD及改进形态滤波方法的轴承故障诊断[J]. 振动与冲击,2015,34(2):38-44.

WU Xiao-tao, YANG Meng, YUAN Xiao-hui, et al. Bearing fault diagnosis using EEMD and improved morphological filtering method based on kurtosis criterion[J]. Journal of Vibration and Shock,2015,34(2):38-44．

[8] Sheen Y T. A complex filter for vibration signal demodulation in bearing defect diagnosis [J]. Journal of Sound and Vibration, 2004, 276(1): 105-119．

[9] Fraser A M, Swinney H L. Independent coordinates for strange attractors from mutual information[J]. Phys Rev A,1986,33 (11):34-40．

[10] Cao Liang-yue. Practical method for determining the minimum embedding dimension of a scalar time series[J]. Physical D: Nonlinear Phenomena, 1997, 110 (1/2):43-50.

The study of an incipient fault diagnosis method based on phase space independent component analysis and contribution coefficient of kurtosis

CHEN Jian-guo1, WANG Zhen1, LI Hong-kun2

(1. College of Mechanical Engineering, Dalian University, Dalian 116622, China;2. Institute of Vibration Engineering, Dalian University of Technology, Dalian 116023, China)

An independent component analysis method shares characteristics with the vibration source separation in the analysis of a signal. However, because the coefficient fault signal of mechanical equipment has the characteristics of strong background noise and a complex vibration source, the independent component analysis method can’t obtain a satisfied effect that can be applied to extract the coefficient fault from a single channel with a strong background noise signal. Therefore, the phase space of the independent component method is proposed to separate and reconstruct the incipient fault signal. The contribution coefficient of kurtosis is then proposed to extract the incipient fault characteristic information from the reconstructed signal. This method is applied to the incipient fault signal of the bearing in the extruder’s gearbox. The incipient fault character information is then extracted successfully, and the faulty component is identified accurately. The experiments show that the phase space of independent component analysis and the contribution coefficient of the kurtosis method offer a feasible research direction for the incipient fault detection.

phase space of independent component analysis; kurtosis; contribution coefficient of kurtosis; incipient fault

10.13465/j.cnki.jvs.2016.12.024

国家自然科学基金(51175057);辽宁省教育厅一般项目(L2013477)

2015-04-17修改稿收到日期：2015-06-11

陈建国 男，博士，讲师，1977年1月生

TN912

A