基于局部特征尺度分解谱熵和VPMCD的液压泵退化状态识别

王余奎， 李洪儒， 魏晓斌， 许葆华

(1.空军勤务学院，徐州　221000; 2.军械工程学院，石家庄　050003)

基于局部特征尺度分解谱熵和VPMCD的液压泵退化状态识别

王余奎1,2， 李洪儒2， 魏晓斌1， 许葆华2

(1.空军勤务学院，徐州221000; 2.军械工程学院，石家庄050003)

针对液压泵故障信号的非平稳特性以及其退化状态难以识别的问题，结合局部特征尺度分解与信息熵理论，提出了局部特征尺度分解谱熵的退化特征提取方法，并将基于变量预测模型的模式识别(Variable Predictive Model based Class Discriminate, VPMCD)方法引入到液压泵的退化状态识别。对不同程度故障的液压泵振动信号进行局部特征尺度分解，从得到的内禀尺度分量中提取振动信号的复杂度和随机性度量指标能谱熵、奇异谱熵和包络谱熵，以其作为液压泵的退化特征向量，通过建立VPMCD退化状态识别模型实现液压泵的退化状态识别。仿真信号分析结果验证了所提出的局部特征尺度分解谱熵具有较好的表征液压泵故障退化状态的能力。通过对实测液压泵松靴和滑靴磨损两种故障模式下的退化状态振动信号进行分析验证了提出方法的有效性。

液压泵；退化状态识别；局部特征尺度分解；谱熵；变量预测模型的模式识别

随着维修理论和相关技术的发展，以故障预测技术为核心的基于状态的维修越来越受大家重视[1]，而基于状态的维修需要对其故障程度和发展趋势进行估计。液压泵作为液压系统的“心脏”，其性能好坏影响着整个系统。但现有的液压泵振动信号分析方法多是集中在故障类型识别和故障位置判定上[2-3]。因此研究液压泵故障程度和状态特征之间关系的退化状态识别具有重要的意义[4]。

退化特征提取和状态识别是退化状态识别的两个关键环节，且是故障预测的基础。在机械设备故障退化的不同阶段，其振动信号的复杂性和随机性会发生相应的变化[5]。近年来，许多表征信号复杂度和随机性的指标被用于机械设备的退化状态识别，如分形维数、近似熵、样本熵和排列熵等[6-9]。另外，在机械设备出现故障时其振动信号会表现出较强的非平稳特性，因此有必要采用非平稳方法对振动信号进行预处理。局部特征尺度分解法[10](Local Characteristic-scale Decomposition, LCD)是2012年提出一种新的非平稳信号分析方法，与经验模态分解(Empirical Mode Decomposition, EMD)相比该方法仅采用一次三次样条拟合，运算所需时间缩短且具有更高的拟合精度[11]。针对液压泵发生故障时其振动信号非线性、非平稳的特点，本文将LCD算法与信息熵理论相结合提出LCD分解谱熵的退化特征提取方法。

状态识别方法对退化状态识别的效率和准确率影响很大。神经网络和支持向量机(Supporting Vector Machine, SVM)是常用的状态识别方法，但是神经网络结构和类型的选择很大程度上依赖于先验知识和经验，且对识别精度有很大影响[12]。SVM模式识别效果受其核函数和参数的影响较大，且该算法本质上是二进制算法，对于多类问题求解需做多次二分类，会导致状态识别精度降低[13]。基于变量预测模型的模式识别(Variable Predictive Model based Class Discriminate, VPMCD)方法是由Raghuraj等[14-16]提出的一种新的状态识别方法。该方法基于从原始数据中提取的特征之间的内在关系建立数学模型，且VPMCD具有多种模型形式可以选择，而其中的非线性模型与神经网络、支持向量机等一样，可以用于非线性系统的状态识别。将VPMCD算法用于机械故障模式识别的研究很多，但将该方法用于退化状态识别尤其是液压泵退化状态识别的研究还很少见到报道。对于液压泵退化状态识别，从其振动信号中提取的退化特征之间具有一定的内在关系，并且在故障退化的不同阶段，所提取的退化特征及它们的内在关系都会发生变化。因此，本文将VPMCD算法引入到液压泵的退化状态识别中。

本文将LCD算法与信息熵理论结合提出了LCD分解能谱熵、奇异谱熵和包络谱熵的概念，并将提取的退化特征组成退化特征向量用于区分液压泵不同程度的退化状态；提出将VPMCD算法用于液压泵的退化状态识别。通过仿真和实例进行有效性验证。

1基于LCD分解的退化特征提取方法

1.1LCD分解算法

LCD分解方法假设任何一个复杂的振动信号都能被分解成不同的内禀尺度分量(Intrinsic Scale Component, ISC)，且分解得到的ISC分量中任何两个分量相互独立，则分解得到的所有分量的和就是原振动信号[10]。而每一个ISC分量需要满足的条件包括：

(1) 在该分量的时间数据段内，相邻的极值点符号相异；

(2) 在该分量的时间数据段内，假设极值点序列为Mj(j=1,2,…,S)，而每个极值点对应的时间为tj(j=1,2,…,S)，取任意两个相邻的极大(小)值点(tj,Mj)和(tj+2,Mj+2)做极值关于时间t的函数F：

(1)

式中：j=1,2,…,S。则该函数在时间tj+1处的函数值Fj+1与该处的极小(大)值Mj+1的比值的大小应该近似不变。

以上的两个条件保证了ISC分量的局部对称性，且在两个任意相邻的极值点间具有单一的模态。对于时间序列x(t)(t=1,2,…,N)的分解步骤为：

(1) 确定该时间序列的极值点Mj(j=1,2,…,S)，并计算

(2)

式中：Fj由式(1)定义。

(2) 由于lj的值仅有2到M-1个，需要对两个端点的值l1和ls进行估计，这就需要对时间序列进行延拓。经过延拓可以得到两个端点的极值点(t0,M0)和(ts+1,Ms+1)。根据式(2)计算l1和ls的值，再采用三次样条函数拟合所有的lj(j=1,2,…,S)，即可得到均值曲线Bl1(t)。

(3) 从原信号中将均值曲线分离，即

h1(t)=x(t)-Bl1(t)

(3)

判断h1(t)是否是一个ISC分量，如果是则输出h1(t)并令ISC1=h1(t)。否则将h1(t)作为原始数据，重复上述步骤，直到h1j(t)是一个ISC分量，并记ISC1=h1j(t)。

(4) 将ISC1从原始数据中分离，即

μ1(t)=x(t)-ISC1

(4)

式中：μ1(t)是剩余信号。

(5) 将μ1(t)看作原始信号，重复上述步骤(1)～(4)n-1次,直到剩余信号为一单调信号或常数，则下式成立

(5)

LCD算法中均值曲线的计算中只用了一次三次样条拟合，与EMD算法相比其拟合的误差更小且具有更高的效率。

1.2LCD分解谱熵

对信号进行LCD分解是在不同的尺度与频率下对其进行划分，实现信号能量在不同尺度上的分布，分析该能量分布的概率信息即可提出LCD分解谱熵的概念。1.2.1LCD分解能谱熵

对原信号进行LCD分解，可得到多个ISCk(k=1,2,…,n)分量，即不同尺度下的信号分量。计算各尺度下ISCk的能量Ek，得到LCD分解能谱E=[E1,E2,…,En]，即是对信号能量在各尺度上的划分，引入信息熵的概念得到了LCD分解能谱熵的定义：

(6)

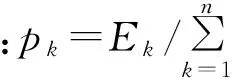
1.2.2LCD分解奇异谱熵

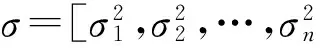
(7)

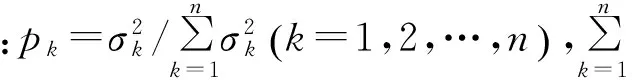
1.2.3LCD分解包络谱熵

对振动信号做LCD分解得到的ISC分量是平稳的单分量信号，采用Hilbert方法对ISC分量进行包络分析可以得到该分量的包络谱。对于同一故障模式下不同程度故障的液压泵振动信号，经过LCD分解后其主要ISC分量在包络域的频率分布均匀程度也各不相同，基于该情况结合信息熵理论提出了LCD分解包络谱熵的概念。对于某振动信号x(i)(i=1,2,…,N)序列，经过LCD分解，得到多个ISC分量，对于其任意一个分量ISCk，其包络谱熵的定义为：

对振动信号LCD分解得到的ISC分量中，只有部分ISC分量包含设备的状态信息，其它的ISC分量代表信号中的干扰分量和噪声成分。因此，有必要从得到的分量中筛选出敏感ISC作为研究对象，使得从中提取的LCD包络谱熵具有更好的退化状态表征能力。互相关系数(Mutual Correlation Coefficient, MCC)能够反应ISC分量与原信号的相似性，互相关关系数越大说明ISC中包含的状态信息越多，反之亦然[17]。互信息[18](Mutual Information, MI)能从非线性角度度量两个随机变量的广义相关程度，常被用于衡量两个随机变量概率密度函数的相似性。本文综合应用以上两个准则提取振动信号中的敏感ISC分量，计算各ISC和原信号的互相关系数和互信息，并求取二者绝对值的乘积作为该ISC分量的敏感度，取敏感度最大的前两个ISC分量作为敏感分量，然后计算每个ISC分量的包络谱熵作为液压泵的退化特征。

1.3仿真分析

(9)

式中：xis(t)模拟液压泵振动信号中的固有冲击成分；xfs(t)模拟液压泵故障引起的冲击成分[19]；0.06t2xfs(t)模拟液压泵故障的加深过程。设置xd(t)的采样点数为N=40 960，采样频率为1 024 Hz，见图1是其时域波形图。

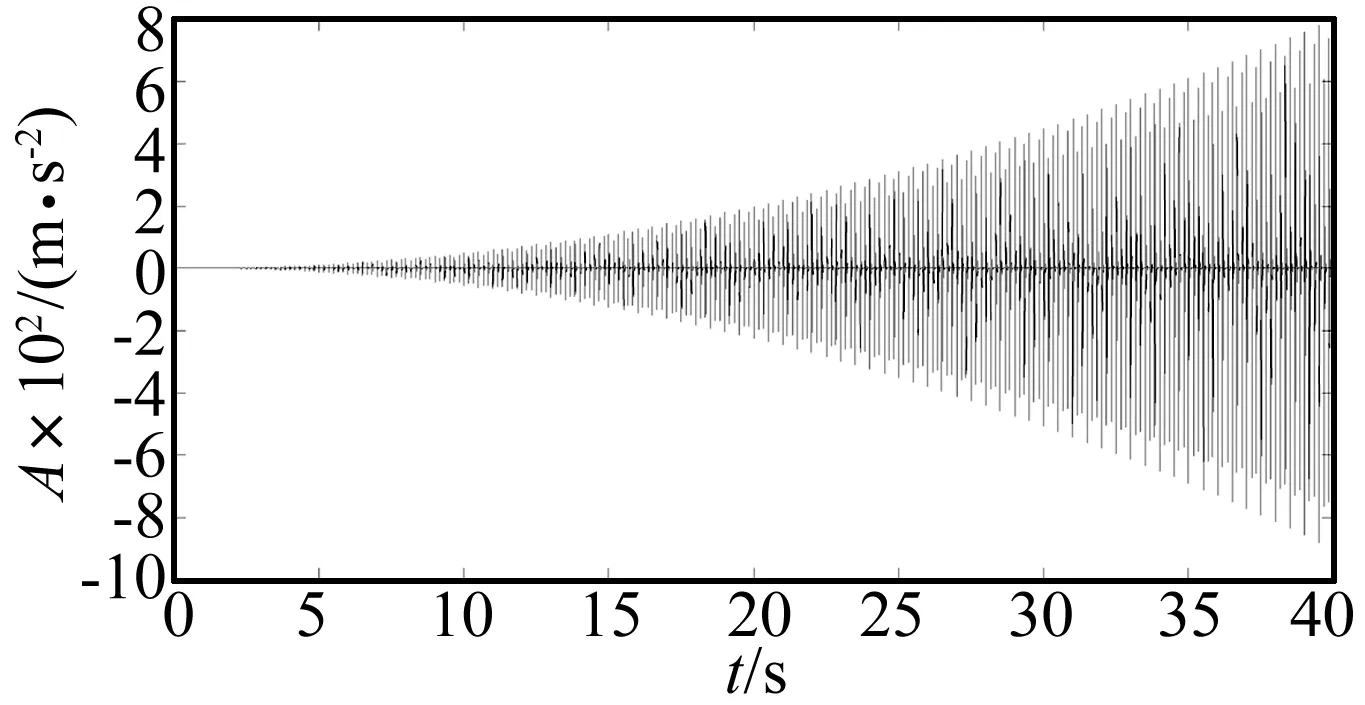
图1　液压泵故障退化仿真信号波形图Fig.1 Wave form of the degradation simulation signal of hydraulic pump

图2　仿真信号LCD分解谱熵Fig.2 LCD decomposition spectrum entropy of simulation signal

2液压泵退化状态识别策略

2.1基于VPMCD的状态识别方法

在VPMCD算法中，特征值yi(i=1,2,…,k)的变量预测模型VPMi可以是线性回归模型也可以是非线性的回归模型，共有以下四种模型可以选择：

(1) 线性模型(L):

(10)

(2) 线性交互模型(LI):

(11)

(3) 二次交互模型(QI):

(12)

(4) 二次模型(Q):

(13)

在以上模型中，r≤k-1是模型的阶数。对于特征向量Y={yi}，任选以上四种模型中的一种，可以采用yj(j≠i)对yi进行预测，得到的预测模型VPMi可以用下式表示：

yi=f(yj,b0,bj,bjj,bjk)+e

(14)

2.2退化状态识别策略

采用VPMCD实现液压泵退化状态识别的策略见图3所示。首先对液压泵振动信号分析提取退化特征集，并将提取特征集分为训练特征集和测试特征集，基于训练特征集建立各退化状态下每个退化特征的VPM模型，并对模型参数进行估计从而得到液压泵的退化状态识别模型，采用建立的模型对测试特征集进行退化状态识别。

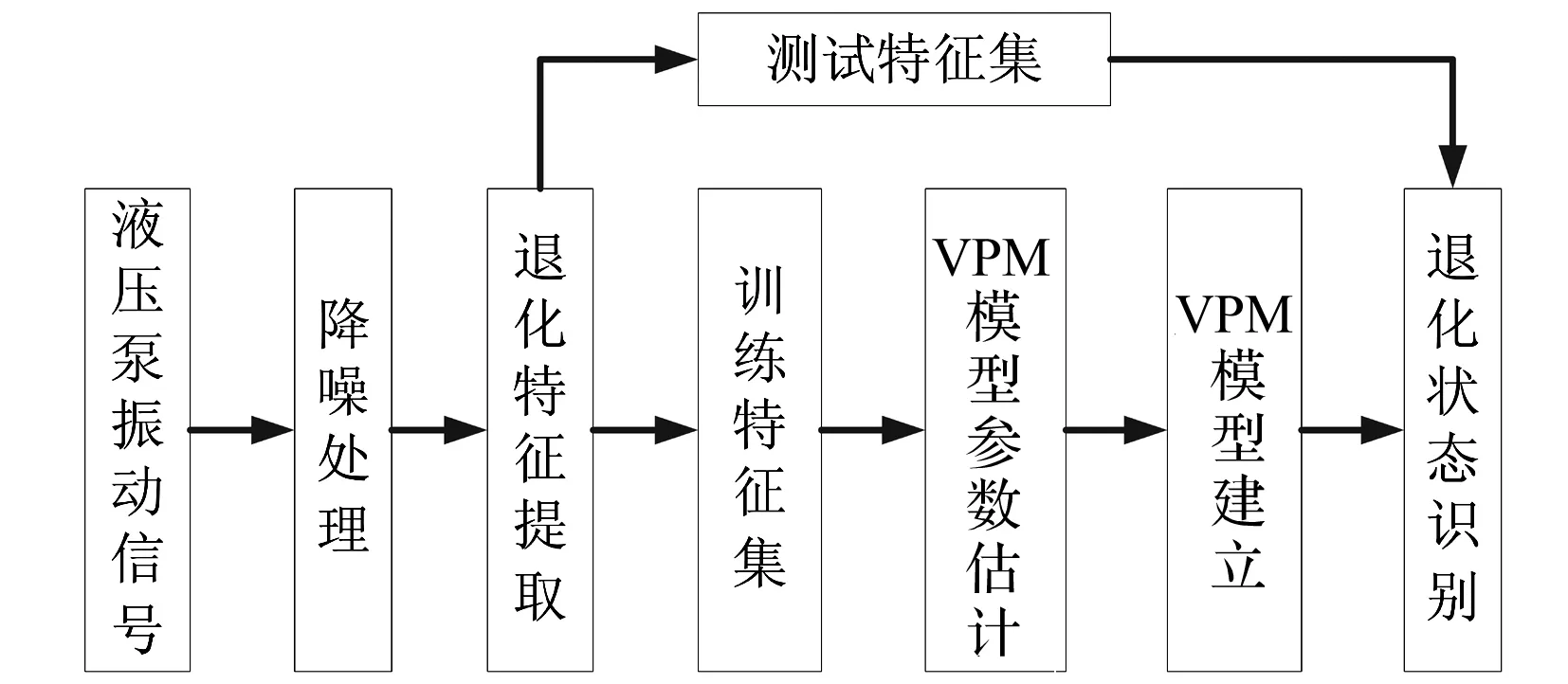
图3　液压泵退化状态识别策略Fig.3 The identification strategy of hydraulic pump degradation state

3实例分析

3.1振动信号采集

实测液压泵振动信号采自液压泵试验台(见图4)。液压泵型号为L10VSO28DFR，其额定转速为1 480 r/min，采用型号为YPT-280M-2的变频电机驱动。选用NI公司的603C01型加速度传感器与液压泵壳体进行刚性连接(见图5)。本文研究主要对液压泵出现松靴或滑靴磨损单故障时的振动信号进行分析。为获得较为真实的振动信号，液压泵退化状态采用装备检修时换下的不同程度松靴和滑靴磨损的柱塞代替正常柱塞的方式模拟。为界定松靴故障的程度，定义松靴度为滑靴与柱塞间能够发生的最大轴向位移量。采用游标卡尺测量试验中所用的5个松靴柱塞的松靴度分别为：0.11 mm,0.18 mm,0.29 mm,0.41 mm和0.54 mm。为界定滑靴磨损的程度，定义滑靴磨损度为滑靴靴帽磨损的值。试验中所用4个滑靴磨损柱塞的滑靴磨损度分别为：0.1 mm，0.14 mm，0.20 mm和0.27 mm。采用NI公司的cDAQ-9171型测量与试验系统采集5种程度松靴故障、4种程度滑靴磨损故障以及正常状态下的液压泵振动信号各200组，每组采样点数为4 096，数据采样频率为50 kHz，采样间隔为30 s，试验过程中试验台主溢流阀压力为10 MPa，电机转速为其额定转速。所采集部分振动信号见图6。

图4 液压泵试验台Fig.4Testbenchofhydraulicpump图5 传感器的安装Fig.5Layoutofsensors

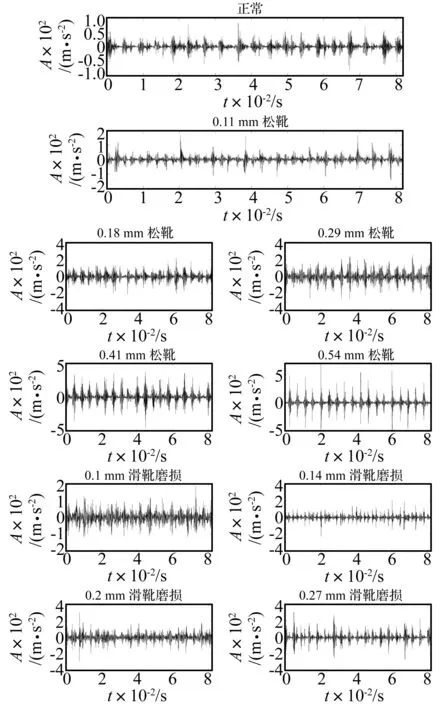
图6　采集的部分振动信号Fig.6 Waveform of collected vibration signals

3.2退化特征提取

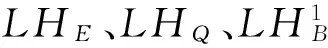
3.3退化状态识别

表1　各ISC与原信号的MCC和MI

图7 提取的敏感ISCFig.7TheextractedsensitiveISC图8 退化样本的LCD谱熵均值Fig.8MeanvalueofLCDspectrumentropyofdegradationstatussamples

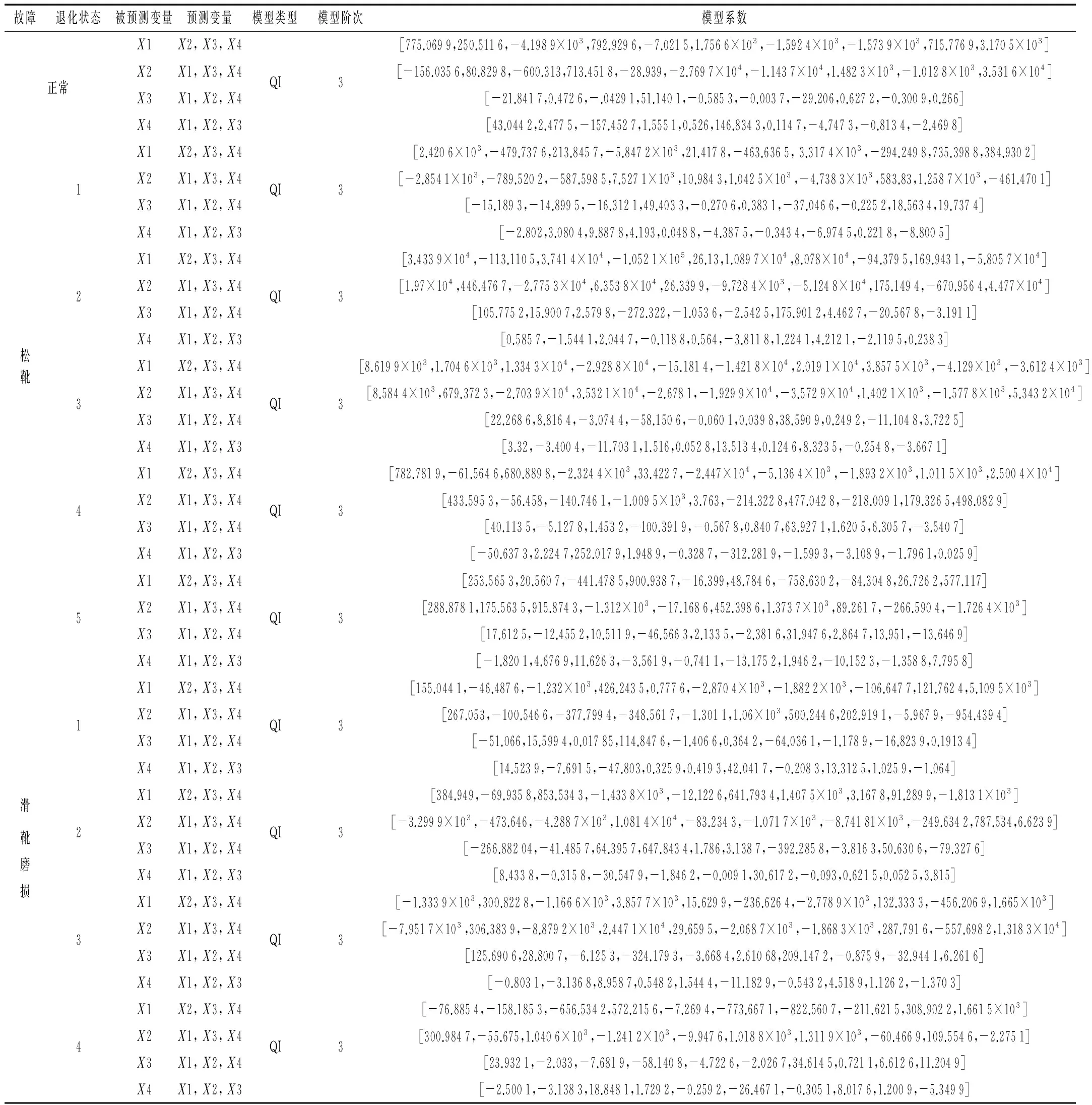
表2　各退化特征值的VPM模型

根据VPMCD算法的模式识别步骤，采用建立的VPM模型对松靴故障和滑靴磨损故障的测试特征集进行识别，并计算每种退化状态下所有特征值VPM模型预测值与真实值的误差平方和，松靴故障退化状态识别结果见表3，表中VPM1～VPM5分别表示松靴故障5种退化状态的模型；滑靴磨损故障的退化状态识别结果见表4,VPM1～VPM4分别表示滑靴磨损故障4种退化状态的模型，两表中VPM0表示正常状态的VPM模型。

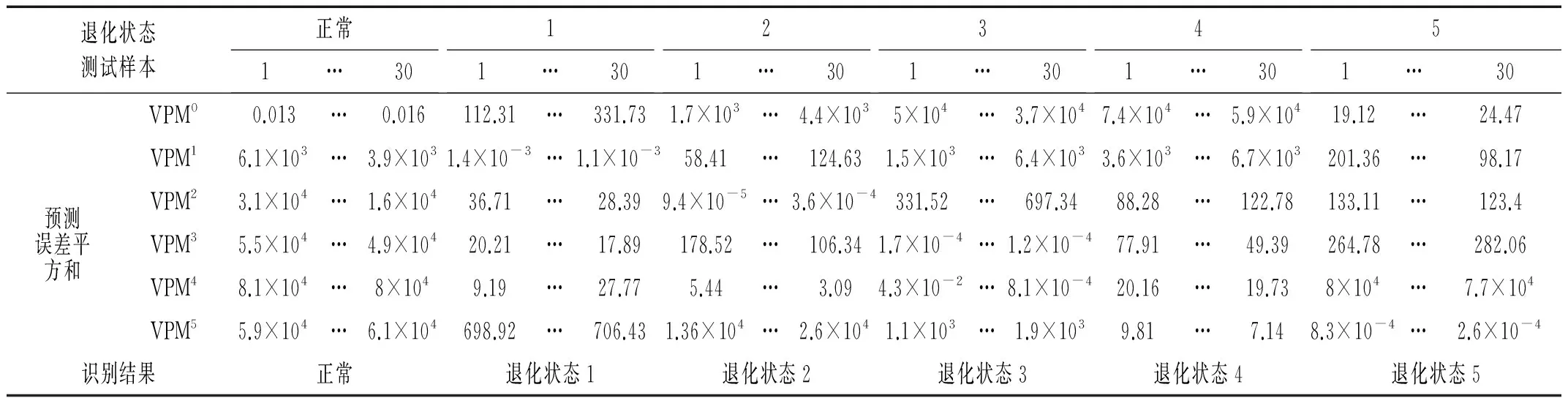
表3　松靴故障退化状态识别结果

表4　滑靴磨损故障退化状态识别结果

分析两种故障模式下测试样本的退化状态识别结果可知，所提出的故障模式识别方法能够很好的识别出液压泵的退化状态，且各种状态的正确识别率都很高。说明基于LCD分解谱熵和VPMCD的液压泵退化状态识别方法用于液压泵退化状态识别具有很好的性能。

4结论

(1) 对液压泵的退化特征提取方法进行研究，在对LCD分解算法分析的基础上将其与信息熵理论结合提出了LCD分解能谱熵、LCD分解奇异谱熵和LCD分解包络谱熵的概念，仿真信号和液压泵实测信号的分析结果验证了所提出LCD分解谱熵具有良好的液压泵故障退化表征能力。

(2) 将VPMCD算法引入到液压泵的退化状态识别中，提出了基于LCD分解谱熵和VPMCD的液压泵退化状态识别方法，对液压泵实测信号分析结果验证了本文提出方法的良好性能。VPMCD算法用于退化状态识别具有很高的建模和状态识别效率；将其用于退化状态识别是对其应用范围的一种拓展。

[1] 张龙,黄文艺,熊国良.基于多尺度熵的滚动轴承故障程度评估[J]. 振动与冲击, 2014,33(9):185-189．

ZHANG Long, HUANG Wen-yi, XIONG Guo-liang. Assessment of rolling element bearing fault severity using multi-scale entropy[J]. Journal of Vibration and Shock, 2014,33(9):185-189．

[2] Du Jun,Wang Shao-ping, Zhang Hai-yan. Layered clustering multi-fault diagnosis for hydraulic piston pump [J]. Mechanical Systems and Signal Processing, 2013,36(2):487-504．

[3] Zhao Zhen,Jia Ming-xing, Wang Fu-li, et al. Intermittent chaos and sliding window symbol sequence statistics-based early fault diagnosis for hydraulic pump on hydraulic tube tester[J]. Mechanical Systems and Signal Processing, 2009,23(5):1573-1585．

[4] 鞠华,沈长青,黄伟国,等. 基于支持向量回归的轴承故障定量诊断应用[J]. 振动、测试与诊断,2014,34(4):767-771．

JU Hua, SHEN Chang-qing, HUANG Wei-guo, et al. Quantitative diagnosis of bearing fault based on support vector regression[J]. Journal of Vibration, Measurement & Diagnosis, 2014,34(4):767-771．

[5] 王冰,李洪儒,许葆华.基于多尺度形态分解谱熵的电机轴承预测特征提取及退化状态评估[J].振动与冲击,2013,32(22):124-128．

WANG Bing, LI Hong-ru, XU Bao-hua. Motor bearing forecast extracting and degradation status identification based on multi-scale morphological decomposition spectral entropy[J]. Journal of Vibration and Shock, 2013,32(22):124-128．

[6] Costa M,Goldberger A L, Peng C K. Multi-scale entropy analysis of biological signals[J]. Physical Review E, 2005, 71：1-18．

[7] Wu S D, Wu C W, Lee K Y, et al. Modified multi-scale entropy for short-term time series analysis[J].Physical A, 2013,392:5865-5873．

[8] 向丹,葛爽. 基于EMD样本熵-LLTSA的故障特征提取方法[J]. 航空动力学报,2014,29(7):1535-1542．

XIANG Dan, GE Shuang. Method of fault feature extraction based on EMD sample entropy and LLTSA[J]. Journal of Aerospace Power, 2014,29(7):1535-1542．

[9] 孙洁娣,肖启阳,温江涛,等. 基于LMD包络谱熵及SVM的天然气管道微小泄漏孔径识别[J]. 机械工程学报,2014,50(20):18-25．

SUN Jie-di, XIAO Qi-yang, WEN Jiang-tao, et al. Gas pipeline small leak aperture classification based on local mean decomposition envelope spectrum entropy and SVM[J]. Journal of Mechanical Engineering, 2014,50(20):18-25．

[10] 程军圣,郑近德,杨宇. 一种新的非平稳信号分析方法——局部特征尺度分解法[J].振动工程学报,2012,25(2):215-220．

CHENG Jun-sheng, ZHENG Jin-de, YANG Yu. A non-stationary signal analysis approach—The local characteristic scale decomposition method[J]. Journal of Vibration Engineering, 2012,25(2):215-220．

[11] 程军圣,杨怡,杨宇. 局部特征尺度分解方法及其在齿轮故障诊断中的应用[J]. 机械工程学报,2012,48(9):64-71．

CHENG Jun-sheng, YANG Yi, YANG Yu. Local characteristic-scale decomposition method and its application to gear fault diagnosis[J]. Journal of Mechanical Engineering,2012,48(9):64-71．

[12] 吴坚,赵阳,何春. 基于支持向量机回归算法的电子机械制动传感器系统故障诊断[J].吉林大学学报, 2013,43(5):1178-1183．

WU Jian, ZHAO Yang, HE Chun. Fault detection and diagnosis of EMB sensor system based on SVR[J]. Journal of Jilin University, 2013,43(5):1178-1183．

[13] 杨宇,王欢欢,曾鸣,等. 基于变量预测模型的模式识别方法在滚动轴承故障诊断中的应用[J].湖南大学学报:自然科学版,2013,40(3): 36-40．

YANG Yu, WANG Huan-huan, ZENG Ming, et al. Application of pattern recognition approach based on VPMCD in roller bearing fault diagnosis[J]. Journal of Hunan University:Natural Sciences,2013,40(3):36-40．

[14] Raghuraj R, Lakshminarayanan S. Variable predictive models—A new multivariate classification approach for pattern recognition application [J]. Pattern Recognition,2009,42(1):7-16．

[15] Raghuraj R, Lakshminarayanan S. Variable predictive model based classification algorithm for effective separation of protein structural classes [J]. Computational Biology and Chemistry,2008,32(4):302-306．

[16] Raghuraj R, Lakshminarayanan S. VPMCD: Variable interaction modeling approach for class discrimination in biological system [J]. FEBS Letter,2007,581(5):826-830．

[17] 苏文胜,王奉涛,张志新,等. EMD降噪和谱峭度法在滚动轴承早期故障诊断中的应用[J].振动与冲击,2010,29(3):18-21．

SU Wen-sheng, WANG Feng-tao, ZHANG Zhi-xin, et al. Application of EMD de-noising and spectral kurtosis in early fault diagnosis of rolling element bearings[J]. Journal of Vibration and Shock, 2010,29(3):18-21．

[18] 张志刚,石晓辉,施全,等. 基于改进EMD和谱峭度法滚动轴承故障特征提取[J]. 振动、测试与诊断,2013,33(3):478-482．

ZHANG Zhi-gang, SHI Xiao-hui, SHI Quan, et al. Fault feature extraction of rolling element bearing based on improved EMD and spectral kurtosis[J]. Journal of Vibration, Measurement & Diagnosis, 2013,33(3): 478-482．

[19] Wang Yu-kui, Li Hong-ru, Ye Peng. Fault feature extraction of hydraulic pump based on CNC de-noising and HHT [J]. Journal of Failure Analysis and Prevention, 2015,15(1):139-151.

Degradation state identification of a hydraulic pump based on LCD decomposition spectrum entropy and VPMCD

WANG Yu-kui1,2, LI Hong-ru2, WEI Xiao-bin1, XU Bao-hua2

(1. Air Force Logistics College, Xuzhou 221000, China;2. Ordnance Engineering College, Shijiazhuang 050003, China)

The paper aims to solve the difficult identification problem of the degradation state and its non-stationary characteristics for a hydraulic pump and. The local characteristic scale decomposition spectrum entropy, as a novel degradation feature extraction method, is proposed based on the combination of local characteristic scale decomposition arithmetic (LCD) and information entropy theory. The variable predictive model-based class discriminate method is adopted as an innovative degradation state identification method. The local characteristic scale decomposition is performed on the hydraulic pump vibration signal at different fault levels. The power spectrum entropy, the singular spectrum entropy and the envelope spectrum entropy are extracted from the obtained intrinsic scale components and are used as the degradation features of the pump. Then, the degradation state identification model is established based on the VPMCD method and the degradation features, allowing the degradation state of the pump to be identified. The analysis result of the simulation signal verified the preferable performance of the proposed local characteristic scale decomposition spectrum entropy as a way of reflecting the degradation state of the pump. The analysis result of the practical vibration signal of the pump with different fault levels, a loose boot fault and a piston shoe wear fault demonstrate the availability of the proposed method.

hydraulic pump; degradation state identification; local characteristic-scale decomposition (LCD); spectrum entropy; variable predictive model based class discriminate (VPMCD)

10.13465/j.cnki.jvs.2016.12.030

国家自然科学基金资助项目(51275524)

2015-04-29修改稿收到日期：2015-06-25

王余奎 男，博士生，1987年生

李洪儒 男，博士生导师，1963年生

TH322；TP306+.3

A