转向系统传递函数的研究及理想传动比获取

程　准,鲁植雄,龚佳慧,刁秀永

(南京农业大学 工学院,江苏 南京 210031)



转向系统传递函数的研究及理想传动比获取

程准,鲁植雄,龚佳慧,刁秀永

(南京农业大学 工学院,江苏 南京 210031)

基于对新建立的6自由度非线性转向模型的研究,提出采用传递函数代替原转向模型的方法,提出求解传递函数的新方法.利用改进的模拟退火算法求解传递函数,采用不同的插值法建立传递函数的动态参数变化模型,对不同的插值法进行比较.基于得到的转向传递函数模型,针对现阶段获取理想传动比方式的缺陷,提出稳态增益理想传动比动态精确获取方法.研究结果表明,转向传递函数输出的响应曲线与原系统的响应曲线非常吻合,精度极高,该传递函数能够替代原先复杂的系统；动态参数变化模型能够很好地表征传递函数的参数随车速、传动比和转向盘转角的变化关系；理想传动比的动态精确获取能够实时保证在车速和方向盘不断变化下转向增益维持理想的定值.

线控转向; 非线性; 传递函数; 模拟退火算法; 理想传动比

近年来,线控转向技术(steer-by-wire, SBW)不断发展,因为SBW系统具有主动转向的优点,可以满足驾驶员对理想转向特性的需求[1-4].SBW技术使传动比可以自由设计因而大幅度提高了操纵稳定性[5-8],对SBW系统的研究意义深远.由于汽车转向系统呈现非线性特点,模型复杂,造成研究的不便,若能够利用一个简单的等效系统来代替原有复杂的系统,则可以大幅度提高研究的效率.本文提出采用传递函数的方法来精确地描述原复杂系统横摆角速度输出关于方向盘角输入的响应,关于传递函数的求解,提出一种新方法,并举例验证新方法的正确性.

本文基于传统的线性二自由度模型的不足[9-10],建立6自由度非线性转向动力学模型.基于新建立的整车转向模型,采用改进的模拟退火算法求解复杂转向模型的传递函数,再基于不同的车速、方向盘转角和传动比进行大量的仿真实验,并结合Lagrange插值、Hermite插值和Spline插值法获取任意工况下传递函数的参数值,从而得到转向传递函数参数的动态变化模型.通过比较不同插值法的结果,提出最优的插值方式.

本文提出现阶段稳态增益控制中理想传动比获取方式的不足,利用转向传递函数模型实时地根据方向盘转角和车速的变化,动态获取理想转向传动比,以精确控制转向横摆角速度增益为理想的恒定目标值.

1　非线性6自由度转向模型

1.1前轮角输入至横摆角速度输出模型

假设车辆在前轮转角δ的输入下作圆周运动,建立如图1所示的转向模型.

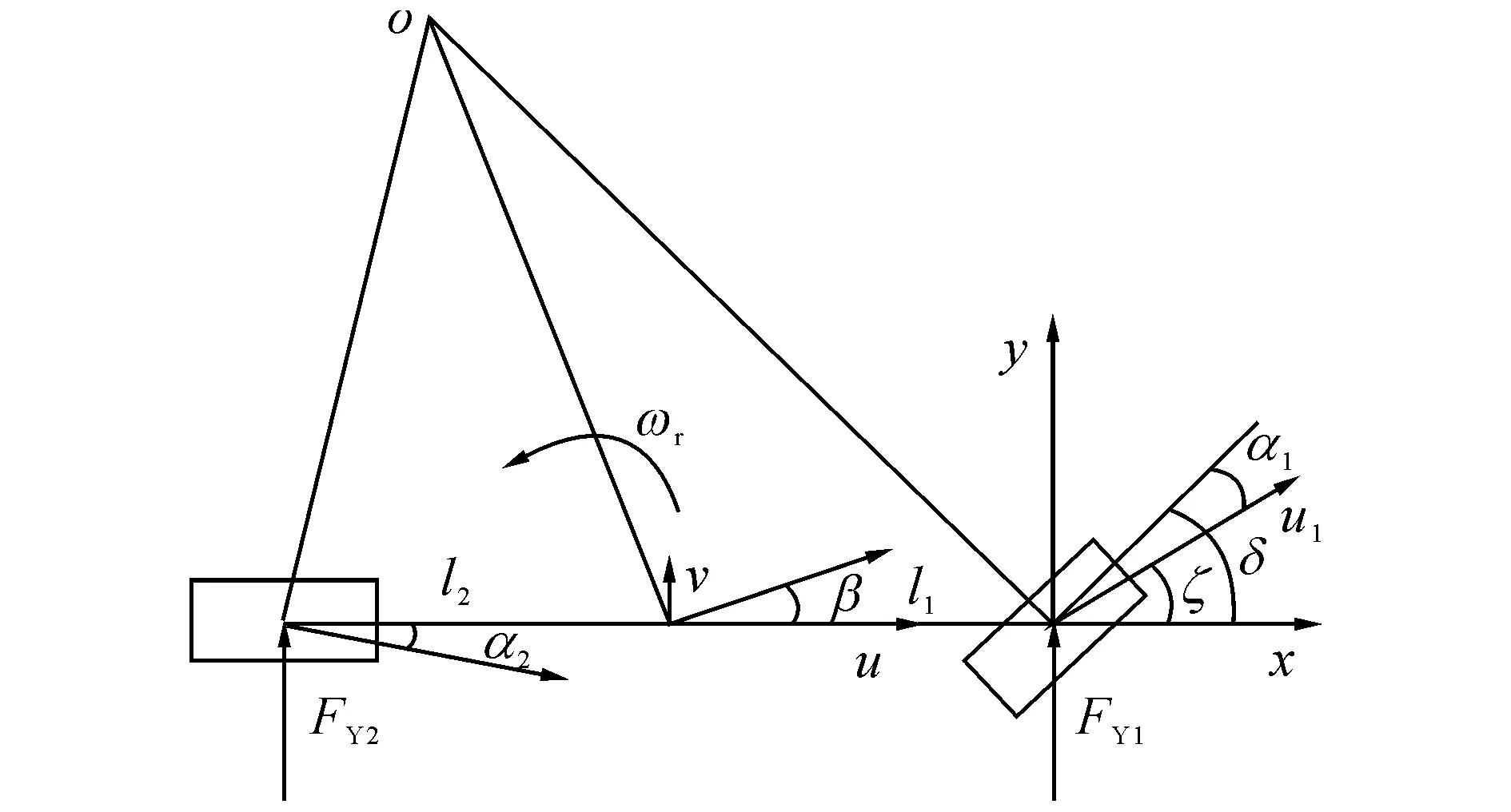
图1　车辆转向模型Fig.1　Vehicle steering model

为了便于研究,作出如下假设.

1)忽略空气阻力的影响.

2)忽略悬架的作用,不考虑车辆行驶时侧倾和俯仰作用的影响.

3)忽略汽车垂向运动的作用.

4)车辆前、后车轮的特性相同.

研究的车辆为前轮转向驱动的汽车.设前轮车速u1为整车模型的输入速度,驾驶员通过踩踏油门踏板来控制的车速为u1.车体质心位置处的车速沿x、y轴正交分解的车速分别设为u和v,β为质心处的侧偏角,α1和α2分别为前、后车轮的侧偏角,可得车体质心速度u与前轮速度u1的关系式：

u=u1cos(δ-α1).

(1)

轮胎与地面之间的侧向力FY(α1)和FY(α2)是一个非线性力,以Magic Formula模型作为侧向力输入模型[11],所以侧向力FY(α)的公式为

FY(α)=Dsin{Carctan[BX-

E(BX-arctan(BX))]}+Sv,

(2)

X=α+Sh.

(3)

式中：B、C、D和E为与侧向力相关的系数,其值与外倾角γ和单个车轮所受的垂直载荷有关；Sv为曲线垂直方向漂移；Sh为曲线水平方向漂移；α为车轮侧偏角.前、后车轮侧偏角为

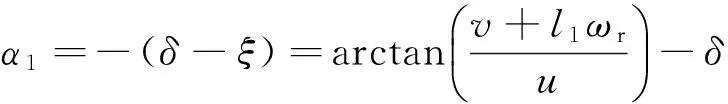
(4)

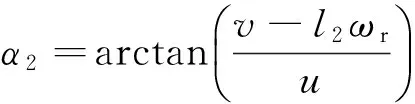
(5)

式中：l1、l2分别为前、后车轴至质心的距离,ξ为u1与x轴的夹角,ωr为横摆角速度.

根据达朗伯原理,建立动力学方程如下：

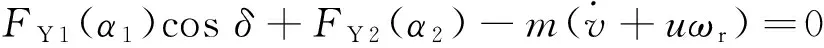
(6)

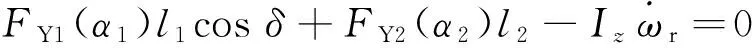
(7)

1.2方向盘角输入至前轮角输出模型

从方向盘角输入至前轮角输出,中间主要由操纵机构、转向器和传动机构起作用.为了提高系统模型的精度,只选取起突出作用的部件[12],本文采用的线控转向系统及数学模型的主要参数均来自文献[13],转向盘模型主要由转向柱末端和路感电机通过减速齿轮啮合来组成；转向执行系统简化为齿轮齿条组件和转向前轮组件；路感电机和转向执行电机均采用直流电机.

基于MATLAB/Simulink的模型建立如图2所示.

2　基于改进的模拟退火算法求解未知的传递函数模型

2.1改进的模拟退火算法

模拟退火算法(simulated annealing algorithm,SA算法)是一种以得到全局最优解为目的的智能算法[14-16]. 模拟退火算法的一般步骤为先设置初始温度T0和最低温度Tf,确认模型所涉及参数的定义域,并在定义域内随机产生一组初始参数值η0=(η01,η02,…,η0n),将其代入公式计算目标函数值ΔE(η0).给予初始参数值一定的扰动,得到新参数组η1=(η11,η12,…,η1n),重新代入计算目标函数值ΔE(η1),并将新函数值与原函数值相减得到ΔE=ΔE(η1)-ΔE(η0).若ΔE<0,则新参数被接受；若ΔE>0,则新参数以概率P=exp(-ΔE/T)被接受.在同一温度T下,重复若干次扰动后,再缓慢降低温度,直至下降到最低温度Tf,停止运算,输出最优解.

本例由于待求解的系统较复杂,为了快速得到最优解,对SA算法进行改进.改进措施主要分为两点.1)改变算法终止条件,将原先目标函数值越接近于0越优,改为目标函数的值小于ε,其中ε为满足需求条件的一个理想值；2)借鉴遗传算法中非均匀变异的思想改变对参数的扰动函数,强化局部搜索能力.扰动函数如下：

ηi+1=ηi+z(rand-0.5)r，

(8)

r=0.1(T/N).

(9)

式中：z=(z1,z2,…,zj),其中zj为第j个参数的定义域长度；T为当前温度；N为从初始温度下降到最低温度进行的迭代总次数.

举例说明利用改进的SA算法求解未知系统传递函数的方法,若已知传递函数为

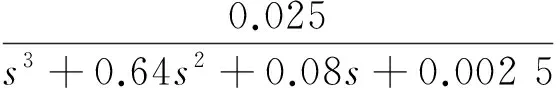
(10)

设传递函数的表达式为

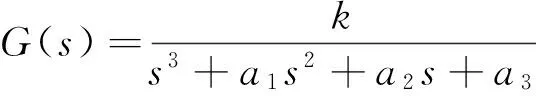
(11)

式中：k、a1、a2、a3为未知待求参数.

用阶跃信号作为原系统的输入,得到输出响应曲线y0.利用改进的SA算法对k、a1、a2、a3进行寻优,目标函数设为每次寻优过程得到的输出响应曲线y1与y0曲线的可决系数R2.得到的迭代进化图和输出曲线的比较图分别如图2、3所示.图中，y为输出响应.

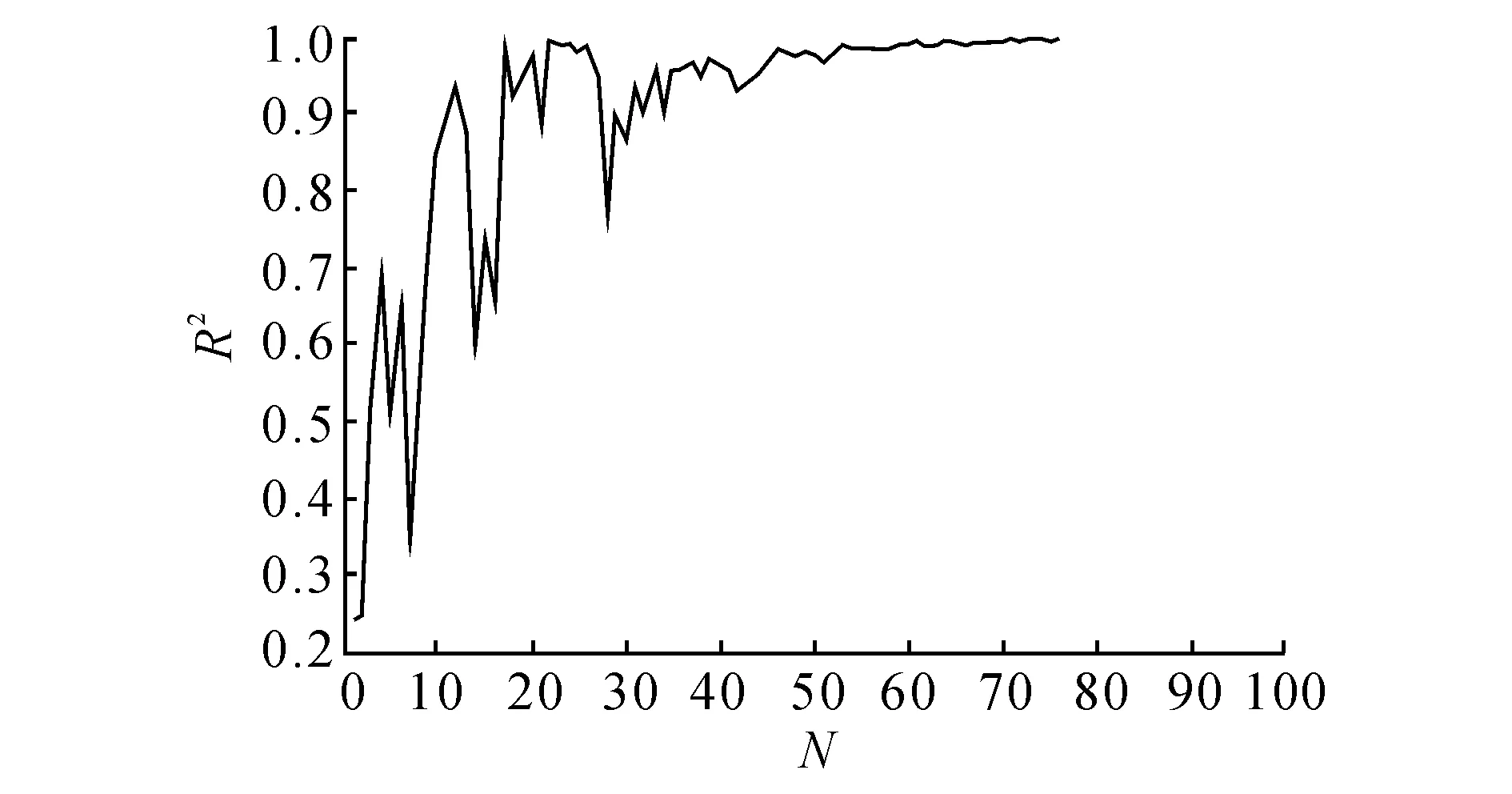
图2　改进的SA算法迭代进化图Fig.2　Improved SA algorithm iterative evolution graph

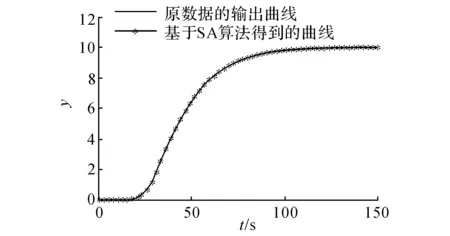
图3　原系统和基于改进的SA算法得到的输出曲线图Fig.3　Output curve of original system and improved SA algorithm

计算得到的结果为k=0.026 8,a1=0.671 2,a2=0.086 0,a3=0.002 7,R2=0.999 97,与原模型的参数非常吻合,而且输出曲线基本重合,改进的SA算法迭代进化次数只有92次.

2.2转向非线性系统等效的传递函数的形式

由于传递函数的形式众多,确定汽车转向模型的传递函数的统一形式非常重要.根据文献[17]可知,传统的线性二自由度转向模型的传递函数形式为

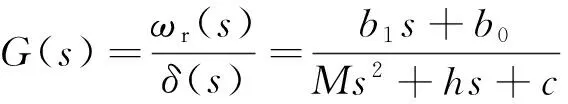
(12)

式中：b1、b0、M、h和c为与整车参数有关的系数.

建立的转向模型具有非线性、复杂等特点,而且实际的车辆模型也具有该特点,所以必须确定等效传递函数的形式.

假设传递函数的形式1为

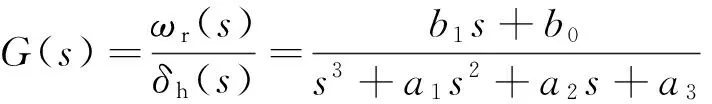
(13)

式中：δh为转向盘转角；b1、b0、a1、a2和a3为未知待求参数,且应与整车参数有关.

采用改进的SA算法求解b1、b0、a1、a2和a3的最优值.由于该转向模型输出的横摆角速度收敛,根据稳定的性质以及类比式(12)中相关参数与整车参数相关的性质,b1、b0、a1、a2和a3皆为正数.在同工况下,即δh、驱动轮车速u1和方向盘转角与前轮转角的角传动比i都相同,将由传递函数输出得到的ωr响应曲线和原系统输出得到的ωr响应曲线进行对比,以两条曲线的可决系数R2作为目标函数来评价相关性和精度.

假设传递函数的形式2为

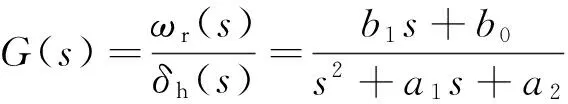
(14)

式中：b1、b0、a1和a2为未知待求参数.

假设传递函数的形式3为

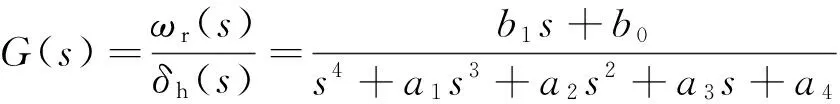
(15)

式中：δh为转向盘转角,b1、b0、a1、a2、a3和a4为未知待求参数.

假设传递函数的形式4为

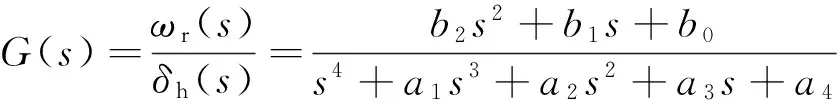
(16)

式中：δh为转向盘转角,b2、b1、b0、a1、a2、a3和a4为未知待求参数.

以u1=80 km/h,δh=30°,i=2为实验工况,基于改进的SA算法得到各个传递函数模型的计算结果,如表1所示.

表1　不同模型的计算结果比较

转向模型的等效传递函数可以用式(14)来精确地描述,模型的精度R2=0.998 4,这与式(12)的形式一致.不同模型的最优输出响应曲线与原系统的响应曲线如图4所示.从图4可以看出,模型2输出的响应曲线与原系统的响应曲线基本重合.

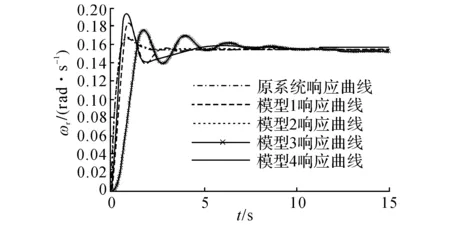
图4　不同模型与原系统的输出响应曲线Fig.4　Output response curves of different models and original system

2.3传递函数中参数的动态变化模型

整车参数如整车质量、绕汽车质心z轴的转动惯量、转向盘转动惯量等参数一经设定,在汽车的行驶过程中一般是不会发生改变.式(14)传递函数中的参数b1、b0、a1和a2的值与整车参数有关,若汽车行驶的工况不变,则参数b1、b0、a1和a2不会变化,所以会影响b1、b0、a1和a2值的因素共有3个,分别为汽车行驶速度、转向盘转角以及转向盘转角和前轮转角之比(即传动比).为了精确地获得不同工况下的转向传递函数,针对不同的车速、转向盘转角和传动比对转向传递函数中的参数基于改进的SA算法进行求解.

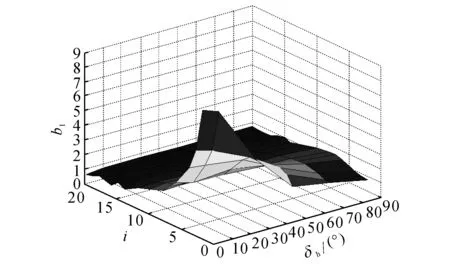
图5　20 km/h车速下的b1参数值Fig.5　b1 parameter values under speed of 20 km/h

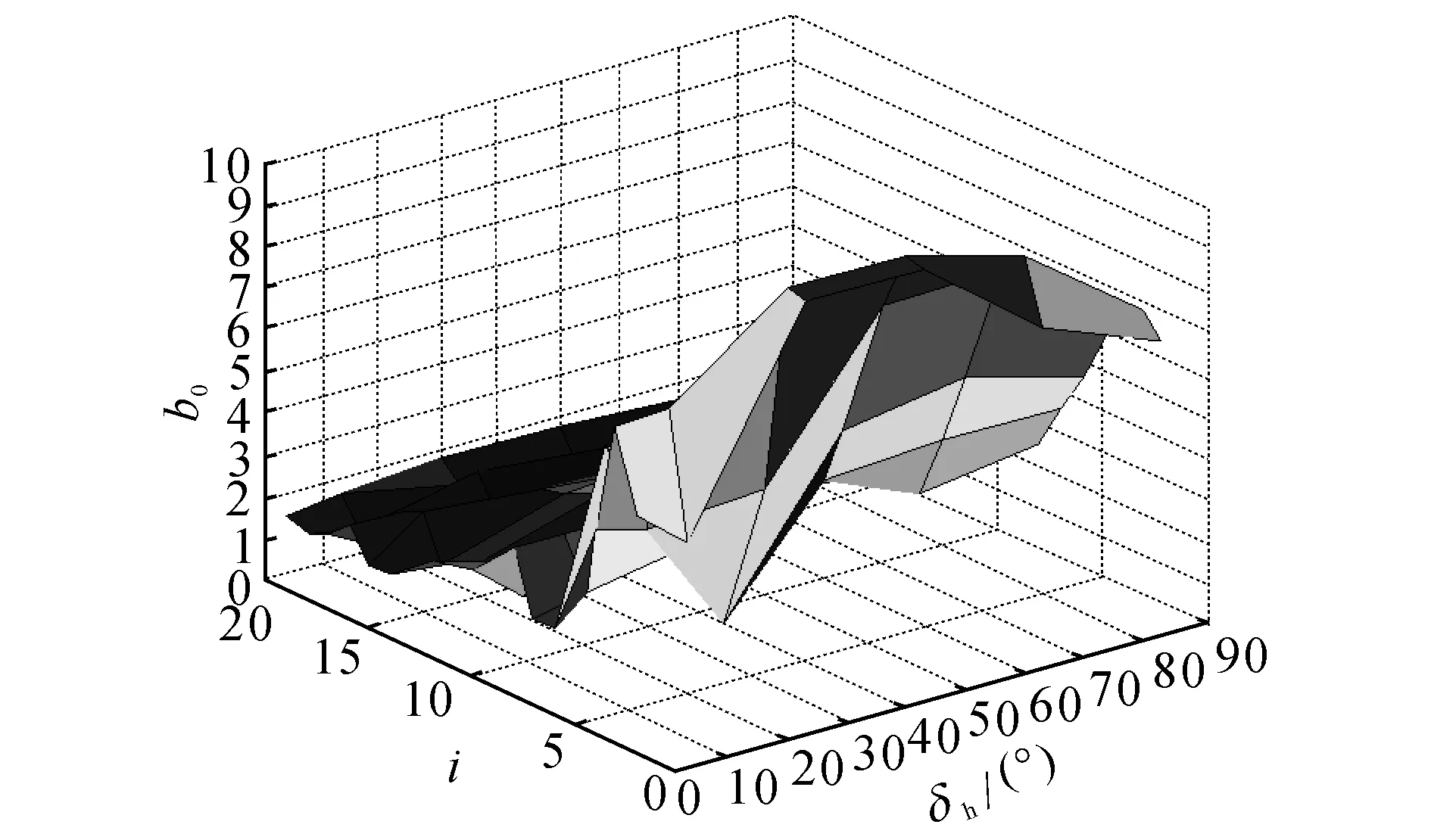
图6　40 km/h车速下的b0参数值Fig.6　b0parameter values under speed of 40 km/h

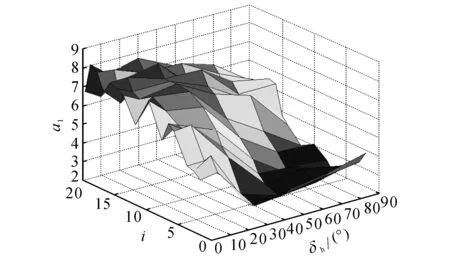
图7　60 km/h车速下的a1参数值Fig.7　a1 parameter values under speed of 60 km/h

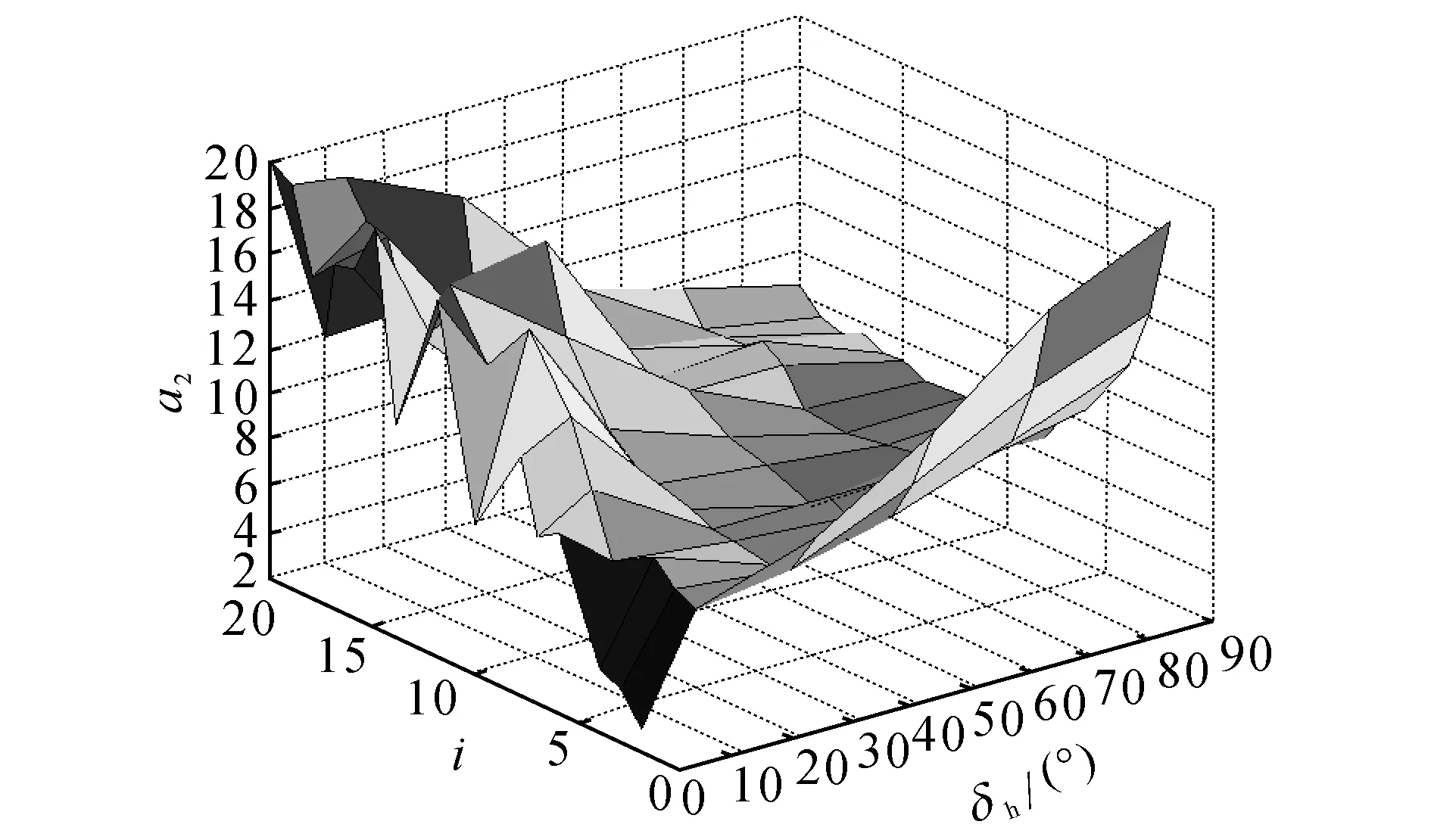
图8　80 km/h车速下的a2参数值Fig.8　a2parameter values under speed of 80 km/h

选择车速、转向盘转角和传动比分别为0～120 km/h、0～90°和2～20.输出的部分车速下的转向传递函数部分参数值如图5～8所示.图中，i为传动比，δh为转向盘转角.

如图9所示为在100 km/h车速下,不同转向盘转角和传动比对应的目标函数R2,所求R2的均值为0.974 0,最大值为0.999 8,最小值为0.92,故所求的转向传递函数都能够较好地代替原有复杂的转向系统.

由于车速、转向盘转角和传动比在每次迭代计算时都是作为离散的数据输入到仿真的算法中,为

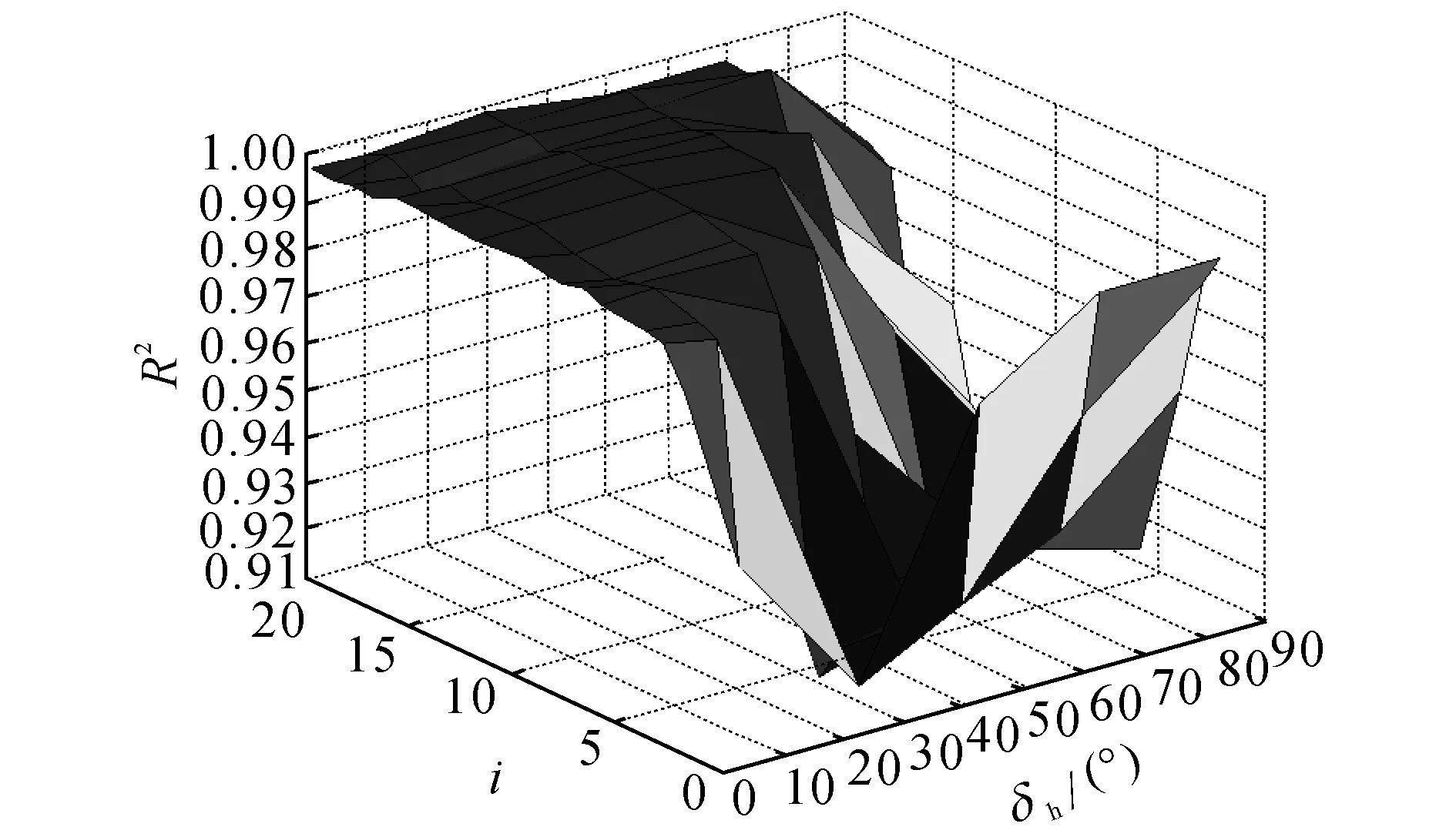
图9　100 km/h车速下的R2值Fig.9　R2 values under speed of 100 km/h

了减少计算的量,同时获得更多可靠的结果,采用内插法来获得更密集的不同工况下转向传递函数的参数值.

插值方法有很多,本文分别采用Lagrange插值、Hermite插值和Spline插值对原先离散的转向传递函数中的参数进行数据处理.为了对比不同插值法的精度,任意选取3种工况进行比较,结果如表2和图10所示.

通过以上对比可知,在一般情况下,基于3种插值法获得的横摆角速度响应曲线与原系统的响应曲线精度都较高, 表明转向传递函数还原系统模型的效果较好.Lagrange插值法在某些工况下可能会产生失效的情况,即转向盘转角信号经过转向传递函数后得到的横摆角速度响应曲线与原系统存在一些误差.通过Hermite插值和Spline插值得到的结果都与原系统的响应曲线比较吻合,Hermite插值获得的结果精度更高.

表2　所选3种工况的参数及计算结果

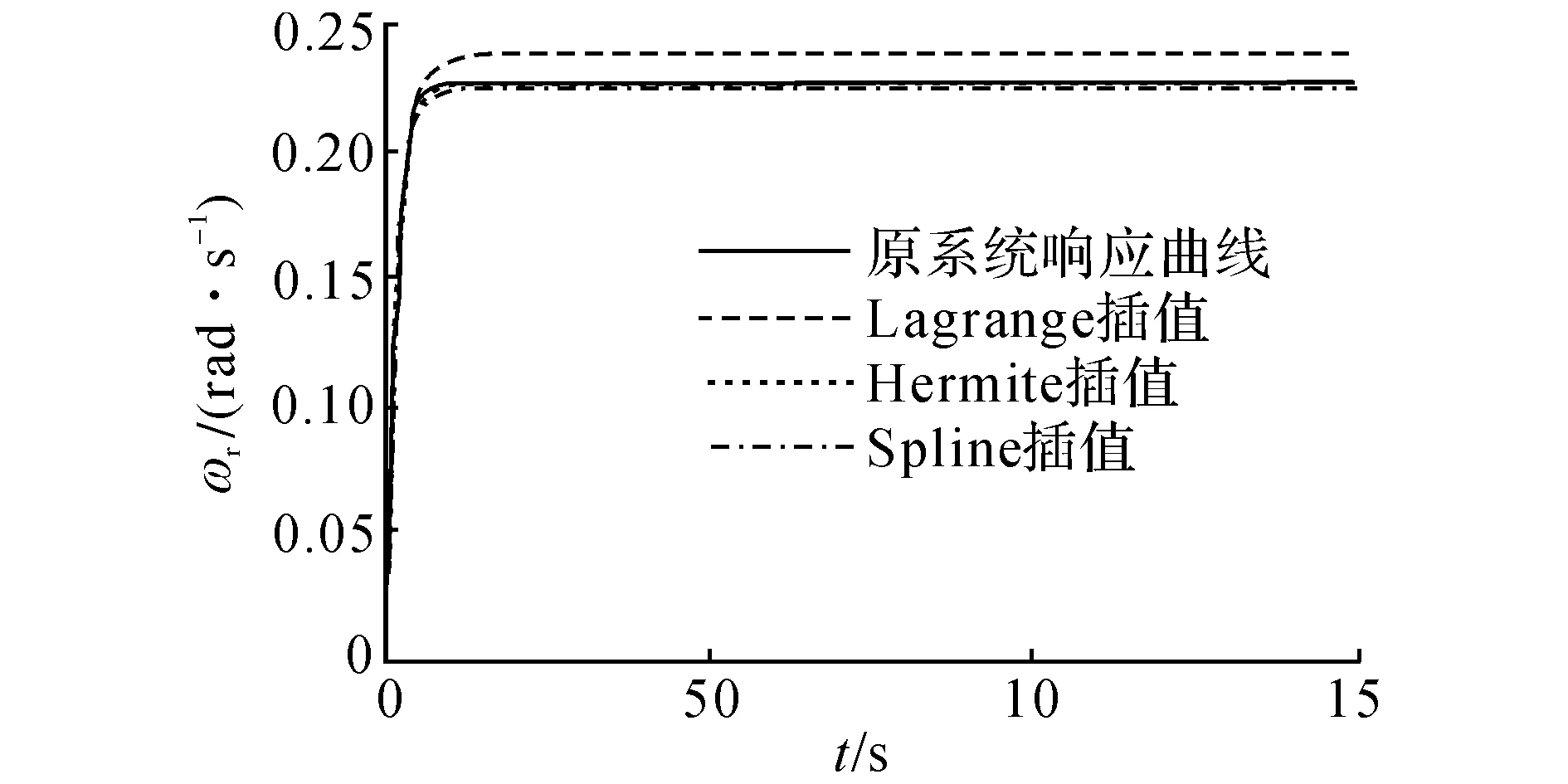
图10　工况3下不同插值法输出的响应曲线Fig.10　Response curves of different interpolation methods under condition 3

3　基于转向传递函数的理想角传动比控制

3.1理想转向传动比的概念和现阶段获得理想传动比的不足

在转向过程中,若ωr与δh的比值不随行驶速度而变化,即ωr/δh恒为一定值,则对于该过程的控制称为转向增益稳态控制[18-20],设该定值为ks.转向增益稳态控制在很大程度上减轻了驾驶员的操纵车辆所带来的负担,基于SBW系统可以通过调节控制i来保证ωr/δh在任意工况下都为定值,这种使稳态横摆角速度增益为定值的传动比称为理想传动比.

现今对于理想转向传动比的计算大部分都采用如下公式：

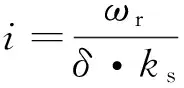
(17)

采用式(17)获取理想传动比i存在以下3个方面的不足.

1)该方法忽略了SBW系统中δh至前轮转角δ之间的响应过程,当驾驶员转动方向盘时,前轮转角不是随之突然就达到相应的值,而会经历一定的响应阶段才最终收敛于目标值.

2)车速和转向盘转角都是离散的概念,所以初期获得的理想传动比本身是离散的,需要在车速和转向盘转角的范围内基于最小二乘法获取其他工况下的理想传动比,但不能保证此时获取的传动比可以满足横摆角速度增益不变.

3)通过式(17)得到的只是i与δ对应的关系,需要进一步处理才能转换为i与δh的关系,这增加了数据处理的工作和难度.

3.2基于转向传递函数仿真获取理想传动比

提出的等效转向传递函数模型可以有效地代替原整车方向盘角输入至横摆角速度输出模型,故而可以很方便地直接获得任意工况下的理想传动比,不仅可以满足精度的需求,而且很好地体现整个转向系统“δh→δ→ωr”的响应过程.

获取理想传动比的流程如图11所示.

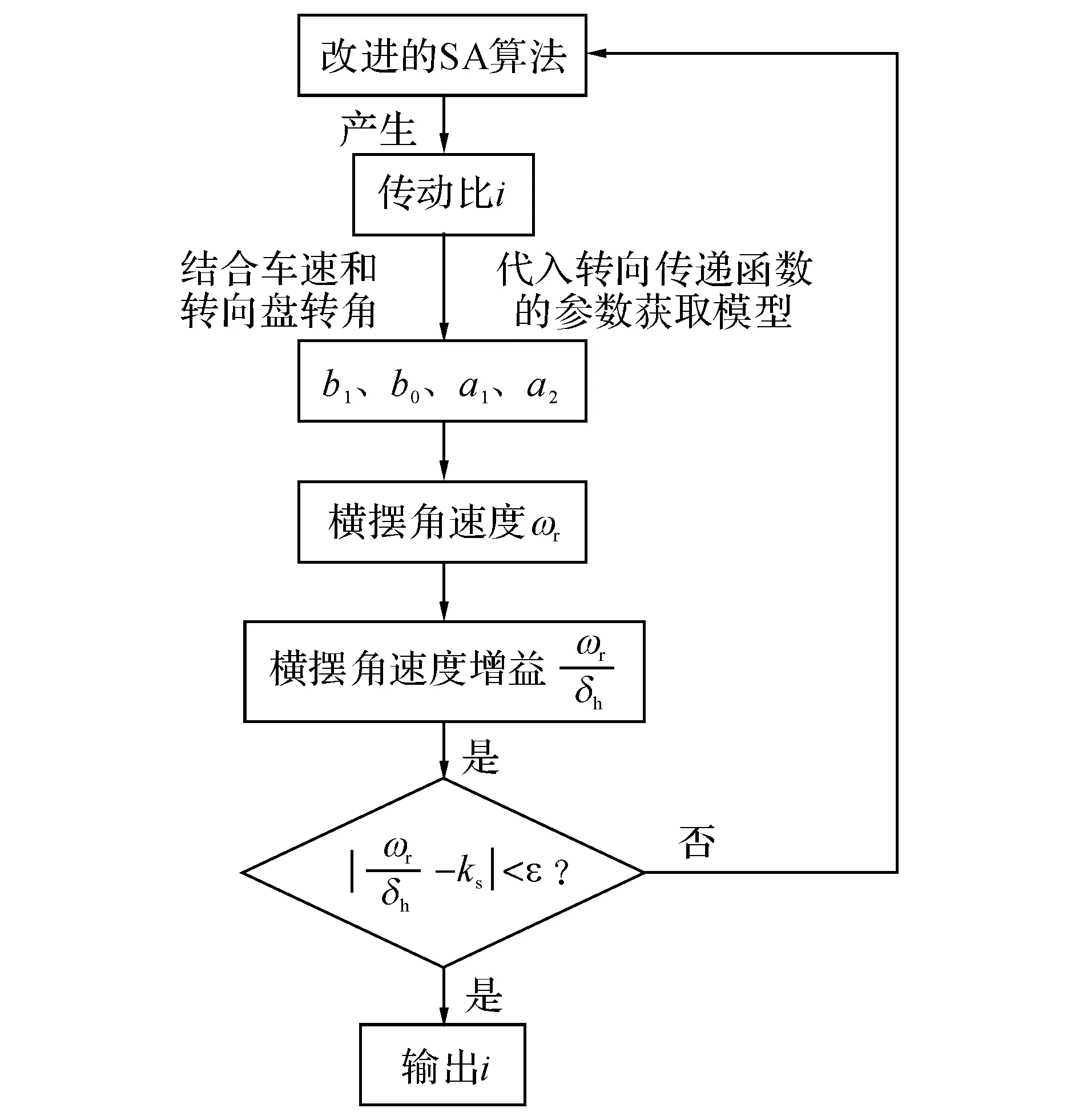
图11　获取任意工况下的理想传动比流程图Fig.11　Ideal transmission ratio flow chart in any working condition

任意选取6种工况进行理想传动比的获取并进行误差计算,ks=0.5,结果如表3所示.

表3所选6种工况下的理想传动比获取及验证结果

Tab.3Ideal transmission ratio and verification results of six operating conditions

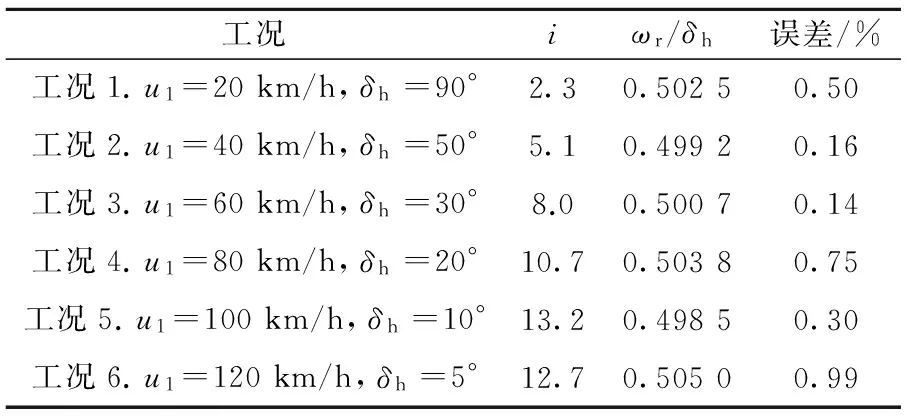
工况iωr/δh误差/%工况1.u1=20km/h,δh=90°2.30.50250.50工况2.u1=40km/h,δh=50°5.10.49920.16工况3.u1=60km/h,δh=30°8.00.50070.14工况4.u1=80km/h,δh=20°10.70.50380.75工况5.u1=100km/h,δh=10°13.20.49850.30工况6.u1=120km/h,δh=5°12.70.50500.99

4　结　论

(1)与传统的车辆转向模型相比,新建立的转向6自由度模型采用了较少的假设,并针对前轮驱动转向汽车而建立,考虑了转向时驱动轮车速对于车体质心速度的影响,能够较好地表征前驱汽车的转向特点.对于转向运动学和动力学方程中的三角函数都未采取简化,以保证角度较大时模型的精度.

(2)通过设计的传递函数,验证了新方法的正确性.计算结果表明,求解得到的传递函数的参数与原参数非常接近,输出响应曲线的可决系数R2=0.999 97,两条曲线基本上完全重合.

(3)采用改进的模拟退火算法,得到的转向传递函数能够较好地代替原复杂的整车转向系统.通过不同工况下的计算结果可知,所求R2的均值为0.974 0,最大值为0.999 8,最小值为0.92.通过分别采用Lagrange插值、Hermite插值和Spline插值法对任意不同工况下转向传递函数的参数进行获取,对比结果可知,Hermite插值法获取的参数值精度最高.

(4)基于转向传递函数对理想传动比进行获取,能克服现阶段传统计算理想传动比的不足,保证实时、精确的获得任意工况下的理想转向传动比以维持转向增益为恒定的目标值.

[1] 郑宏宇,宗长富,王祥. 汽车线控转向系统路感模拟方法[J]. 农业机械学报,2011,42(2)：18-22．

ZHENG Hong-yu,ZONG Chang-fu,WANG Xiang. Road feel design for vehicle steer-by-wire system [J]. Transactions of the Chinese Society for Agricultural Machinery,2011,42(2)：18-22．

[2] 郑宏宇,陈国迎,孙琳琳,等. 基于线控转向系统的路面参数估计[J]. 吉林大学学报：工学版,2014,44(2)：292-295．

ZHENG Hong-yu, CHEN Guo-ying, SUN Lin-lin, et al. Tire-road friction coefficient estimation based on steer-by-wire system [J].Journal of Jilin Universiy: Engineering and Technology Edition,2014,44(2)：292-295．

[3] 鲁植雄,刁秀永,龚佳慧,等. 轮式拖拉机线控液压转向系统路感特性与评价[J]. 农业工程学报,2015,31(12)：57-63．

LU Zhi-xiong,DIAO Xiu-yong,GONG Jia-hui,et al. Assessment and characteristic of road-feeling for wheeled tractor hydraulic steer-by-wire system [J]. Transactions of the Chinese Society of Agricultural Engineering,2015,31(12)：57-63．

[4] 郑宏宇,王祥,宗长富,等. 力控和位置反馈型线控转向系统双向控制策略[J]. 农业机械学报,2014,45(6)：14-19．

ZHENG Hong-yu, WANG Xiang, ZONG Chang-fu,et al. Bilateral control strategy of steer-by-wire system using force control and position deviation feedback [J]. Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(6)：14-19．

[5] ASAI S,KUROYANAGI H,TAKEUCHI S. Development of a steer-by-wire system with force feedback using a distur-bance observer [C]∥ 2004 SAE World Congress. Detroit：[s. n.],2004:1-8．

[6] 于蕾艳,林逸,施国标. 线控转向系统的主动转向控制策略[J]. 农业机械学报,2008,39(1)：4-6．

YU Lei-yan,LIN Yi,SHI Guo-biao. Active steering control strategy of steer-by-wire system [J]. Transactions of the Chinese Society for Agricultural Machinery,2008,39(1)：4-6．

[7] 郑宏宇. 汽车线控转向路感模拟与主动转向控制策略研究[D]. 长春：吉林大学,2009:1-3．

ZHENG Hong-yu. Research on road feeling and active steering control strategy for vehicle steering-by-wire system [D]. Changchun:Jilin University,2009:1-3．

[8] YAMAGUCHI Y,MURAKAMI T. Adaptive control for virtual steering characteristics on electric vehicle using steer-by-wire system [J]. IEEE Transactions on Industrial Electronics,2009,56(5)：1585-1594．

[9] 高举成,张兆合,罗丽君,等. 汽车操纵稳定性的广义汽车转向稳态响应模型[J]. 公路交通科技,2005,22(6)：147-150．

GAO Ju-cheng,ZHANG Zhao-he,LUO Li-jun,et al. A generalized model for vehicle steering steady state response of control stability performance [J]. Journal of Highway and Transportation Research and Development,2005,22(6)：147-150．

[10] 周玉财,何仁,陈士安,等. 考虑空气力的车辆三自由度转向模型与状态方程[J]. 交通运输工程学报, 2009, 9(1)：29-34．

ZHOU Yu-cai,HE Ren,CHEN Shi-an,et al. Three-DOF vehicle steering model and state equations based on considering air forces [J]. Journal of Traffic and Transportation Engineering,2009,9(1)：29-34．

[11] VIJAY ALAGAPPAN A,NARASIMHA RAO K V,KRISHNA KUMAR R. A comparison of various algorithms to extract magic formula tyre model coefficients for vehicle dynamics simulations [J]. Vehicle System Dynamic,2015,53(2)：154-178．

[12] 施国标,申荣卫,林逸. 电动助力转向系统的建模与仿真技术[J]. 吉林大学学报：工学版,2007,37(1)：31-36．

SHI Guo-biao,SHEN Rong-wei,LIN Yi. Modeling and simulation of electric power steering system [J]. Journal of Jilin University: Engineering and Technology Edition,2007,37(1)：31-36．

[13] 唐绍丰. 基于模糊自适应PID控制的汽车线控转向系统研究[D]. 淄博：山东理工大学,2011:11-14．

TANG Shao-feng. Research on automobile steer by wire system based on fuzzy adaptive PID control [D]. Zibo:Shandong University of Technology,2011:11-14．

[14] 刘爱军,杨育,李斐,等. 混沌模拟退火粒子群优化算法研究及应用[J]. 浙江大学学报：工学版,2013, 47(10)：1722-1730．

LIU Ai-jun,YANG Yu,LI Fei,et al. Chaotic simulated annealing particle swarm optimization algorithm research and its application [J]. Journal of Zhejiang University: Engineering Science,2013, 47(10)：1722-1730．

[15] 刘俊玮,王子豪. 基于模拟退火与Dijkstra算法的复杂网状结构供应链最优化研究[J]. 浙江大学学报：理学版,2014,41(2)：149-152．

LIU Jun-wei,WANG Zi-hao. Optimization research of the complex network structure supply chain based on simulated annealing and Dijkstra algorithm [J]. Journal of Zhejiang University: Science Edition,2014, 41(2)：149-152．

[16] 孙士平,曾庆龙,吴建军. 基于改进模拟退火算法的复合材料层合板屈曲优化[J]. 中国机械工程,2015,26(12)：1676-1683．

SUN Shi-ping,ZENG Qing-long,WU Jian-jun. Buckling optimization of composite laminates based on improved simulated annealing algorithm [J]. China Mechanical Engineering,2015, 26(12)：1676-1683．

[17] 余志生. 汽车理论[M]. 北京：机械工业出版社,2009:144-162．

[18] 宗长富,郑宏宇,田承伟,等. 线控转向稳态增益与动态反馈校正控制算法[J]. 汽车工程,2007,29(8)：686-691．

ZONG Chang-fu,ZHENG Hong-yu,TIAN Cheng-wei,et al. Steady-state gain and dynamic feedback correction algorithm for steer-by-wire [J]. Automotive Engineering,2007,29(8)：686-691．

[19] 马建,冯镇,宋宏勋. 基于非线性系统结构稳定性理论的车辆转向动力学研究[J]. 中国公路学报,2015,28(3)：110-116．

MA Jian,FENG Zhen,SONG Hong-xun. Study on vehicle steering dynamics based on structural stability theory of nonlinear system [J]. China Journal of Highway and Transport,2015,28(3)：110-116．

[20] 王春燕,崔滔文,赵万忠,等. 基于理想传动比的主动前轮转向控制[J]. 农业工程学报,2015,31(4)：85-90．

WANG Chun-yan,CUI Tao-wen,ZHAO Wan-zhong,et al. Active front wheel steering control based on ideal transmission ratio [J]. Transactions of the Chinese Society of Agricultural Engineering,2015,31(4)：85-90.

Transfer function of steering system and acquisition method of ideal steering ratio

CHENG Zhun,LU Zhi-xiong,GONG Jia-hui,DIAO Xiu-yong

(CollegeofEngineering,NanjingAgriculturalUniversity,Nanjing210031,China)

The transfer function was used instead of the original steering model based on the new nonlinear steering model of six DOFs. A new method was proposed to solve the transfer function. The improved simulated annealing algorithm was used to solve the transfer function. Then different interpolation methods were used to establish the transfer function parameters’ model of dynamic change. Different interpolation methods were compared with the results. A new method for obtaining the ideal steering ratio was proposed based on the model of the steering transfer function in order to overcome the shortcomings of the current methods. Results showed that the response curve of the steering transfer function accorded with the response curve of the original system, and the transfer function can replace the original complex system. Dynamic change parameter model can characterize the relationship between the parameters of the transfer function with the speed, transmission ratio and steering wheel angle. Dynamic accurate acquisition of ideal steering ratio can guarantee the constant change in the speed and steering wheel to maintain the desired value of the steering gain．

steer by wire; nonlinearity; transfer function; simulated annealing algorithm; ideal steering ratio

2015-06-26.浙江大学学报(工学版)网址： www.journals.zju.edu.cn/eng

江苏省科技支撑计划资金资助项目(BE2012384)；江苏省科技成果转化专项资金资助项目(BA2010055).

程准(1992-)，男，硕士生，从事车辆动力学分析、车辆地面力学的研究.ORCID：0000-0003-1451-9156.

E-mail：chengzhun38@163.com

10.3785/j.issn.1008-973X.2016.07.008

U 463

A

1008-973X(2016)07-1276-08

通信联系人：鲁植雄，男，教授.ORCID：0000-0002-1687-4058. E-mail：luzx@njau.edu.cn