基于流形-奇异值熵的滚动轴承故障特征提取*

2016-08-03王奉涛陈守海闫达文崔立明

振动、测试与诊断 2016年2期

关键词：滚动轴承流形特征提取

王奉涛，　陈守海，　闫达文，　朱　泓，　崔立明，　王　雷

(1.大连理工大学机械工程学院　大连，116023)　(2. 大连理工大学数学科学学院　大连，116023)

基于流形-奇异值熵的滚动轴承故障特征提取*

王奉涛1，陈守海1，闫达文2，朱泓1，崔立明1，王雷1

(1.大连理工大学机械工程学院大连，116023)(2. 大连理工大学数学科学学院大连，116023)

摘要提出一种基于流形-奇异值熵的滚动轴承时频故障特征提取方法。首先,在HHT(Hilbert-Huang transform,简称HHT)时频分析基础上，应用二维流形方法提取信号流行成分以达到对轴承故障特征进行降维和提取敏感参量的目的；然后，定义了奇异值熵来定量衡量不同故障状态下流行成分的差异；最后，将流形奇异值向量与概率神经网络相结合,有效实现了轴承故障样本分类。与一般的考虑欧式空间全局范围最优值的主分量(principal component analysis,简称PCA)方法及以向量为研究对象的一维流形方法不同，该方法直接以二维信息为研究对象，避免了一维流形算法需将二维信息转化为向量带来的信息损失，与PCA方法相比更能发现隐藏在高维数据流形结构中的局部数据特征。工程信号分析验证了该方法的有效性，为准确提取滚动轴承故障特征提供了一种可靠手段。

关键词流形；奇异值熵；特征提取；滚动轴承

引言

滚动轴承是机械结构中不可缺少的重要组成部分，对轴承的运行状态做出准确评估，真正做到预知维修防患于未然具有重要意义[1]。近年来，机械故障状态监测及预知维修技术引起越来越多的关注，而有效的故障状态监测和预知维修以有效提取表征不同故障状态的故障特征为基础[2]。

振动信号分析对轴承进行故障诊断以及模式识别已得到广泛应用[3]。概括起来振动分析方法大致可分为3类，即时域分析方法、频域分析方法和时频域分析方法[4-5]。在实际工况下，机械设备的振动信号大多都是非线性非平稳信号[6-7]。时频分析方法是一种有效处理非线性非平稳信号的方法，能够有效克服常规时、频域方法对瞬变频率信号在整个周期内进行平均的缺点，提高了信号的时频聚集性[8]。近年来，短时傅里叶变换、Wigner-Ville分布、小波分析等时频分析方法被广泛应用于非平稳信号分析领域并取得了一定的成果。但这些方法都存在着不同的缺陷，短时傅里叶变换的平稳性假设及其窗函数是固定的，其不太适合分析对时频分辨率有变化要求的非平稳信号，只能勉强用于分析分段平稳信号或者近似平稳的信号。Wigner-Ville分布的缺点在于对多分量信号来说，其分布会产生不可避免的交叉性[9]。小波分析首先是小波基函数的选取直接影响小波分析的结果，另外基函数是在分析前便选定了，一旦选定在分析过程中便不能更改，所以不具备自适应特性[10]。为克服以上方法的局限性，Huang等[11]提出了经验模式分解(empirical mode decomposition,简称EMD)和Hilbert时频谱的概念，在对EMD分解信号计算瞬时频率的基础上得到了表示信号时频分布特征Hilbert时频谱，由于其频率的瞬时性，Hilbert时频谱非常适合于分析非平稳信号[12]。实际上Hilbert时频谱可以看成定义在时频域的二维图像，在实际应用中可以借助图像特征提取方法进行处理[13]。

此前，Wang等[14]应用时频图像分析原理对齿轮箱的早期故障进行了有效诊断。朱利民等[15]提取二维短时傅里叶时频图的时频特征用以故障诊断，取得了很好的效果。张金玉等[16]应用时频图像对复杂振动状态下的柴油机故障进行了识别分类，得到了满意的效果。李宏坤等[17-18]利用Hilbert谱时频特征对叉车柴油机气缸磨损故障严重程度进行诊断，运用滚动轴承Hilbert时频图的时域、频域、时频域的几何中心作为特征向量，应用支持向量机(support vector machine,简称SVM)理论进行模式分类。但其不但计算量大，且以几何参数作为滚动轴承时频故障特征，缺乏相应的物理意义，仅是一种定性判断。

为克服已有研究的不足，笔者提出一种基于流形-奇异值熵的Hilbert时频谱故障特征提取方法。实际轴承故障信号验证结果表明，该方法能够有效提取代表轴承各类故障特征的时频信息，对诊断滚动轴承各种故障提供一种有效手段。

1理论基础

1.1Hilbert谱分析方法

Hilbert时频谱是在瞬时频率基础上发展起来的，因此首先对瞬时频率的定义进行阐述。

1.1.1瞬时频率的定义

(1)

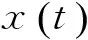
(2)

(3)

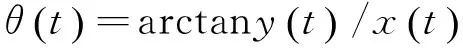
(4)

(5)

为得到信号的Hilbert时频谱，首先需要对信号进行EMD分解，下面简述EMD分解理论。

1.1.2EMD分解的基本原理

(6)

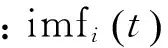
EMD分解出的基本模式分量是按照频率由高到低的顺序排列的，并且满足基本模式分量具有瞬时频率的两个基本限制条件。

在定义了瞬时频率及EMD分解的基础上，下面分析Hilbert时频谱。

1.1.3Hilbert时频谱

将原始信号进行EMD分解，对每个基本模式分量作Hilbert变换，表示成解析信号形式，并且忽略剩余分量

(7)

然后求出每个基本模式分量相应的瞬时频率。最后，把原始信号在Hilbert空间中表示为时间与瞬时频率的函数H(ω,t)，则函数H(ω,t)称为Hilbert时频谱函数，其数学表达式如下

(8)

其中：bi为开关因子，当ωi=ω时，bi=1；当ωi≠ω时，bi=0。

1.2流形理论

1.2.1LPP算法

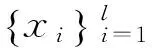
(9)

其中:S为权值矩阵，可以采用k近邻法来定义

(10)

其中：xj为xi的第j个临近点；λ为一个大于0的常量。

对式(9)进行代数变换

WTXLXTW

(11)

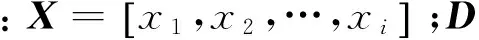
能使式(11)取得最小值的变换矩阵W可以通过求解如下的广义本征值问题而得到

XLXTW=λXDXTW

(12)

1.2.22D-LPP算法

LPP算法只能算是一种针对一维向量的流形特征提取算法，但在时频图等二维图像特征提取过程中，训练图像的数目相对于图像向量的维数而言很小，导致XDXT奇异，LPP算法失效。为此采用一种新的二维LPP(2D-LPP)算法提取时频图的故障特征。

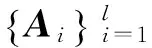
(13)

求解最优w可转化为解决下式本征值问题

(14)

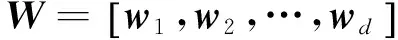
(15)

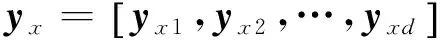
2提取方法步骤

流形方法是以局部最优方法提取高维数据内在本质特征，能够从高维受干扰信号中恢复出信号原始的本质特征。流形方法与常规全局线形降维方法区别在于，流形方法提取高维数据的低维特征是采取一种先局部后整体的方法，可以有效提取高维数据集中蕴含的低维非线性本质数据特征。

笔者提出一种基于二维流形-奇异值熵的滚动轴承故障信号时频故障特征方法，其具体步骤如下：

1) 采集不同工况下的滚动轴承振动信号，对信号进行截取等预处理；

2) 计算各信号的HHT时频谱，为了提高流形算法的计算速度,对时频区域进行网格划分,对每个时频网格内的时频谱能量值进行积分,将信号的HHT时频谱转化为时频能量直方图；

3) 时频能量直方图实际是一个二维矩阵,将样本集信号对应的时频能量直方图组成一个高维时频特征组合；

4) 利用2D-LPP流形算法计算高维时频特征组合的最优投影方向(向量)；

5) 将所有信号的HHT时频谱分别向最优投影方向投影，得到样本HHT时频谱图的低维流行特征矩阵，对特征矩阵做奇异值分解，定义奇异值熵时频特征参数定量刻画；

6) 将训练样本的奇异值向量输入到概率神经网络中对轴承进行故障分类。

3试验

3.1实际轴承信号

为验证本研究方法的有效性，应用美国CaseWesternReserveUniversity大学的轴承故障信号。试验台装置如图1所示。

图1　轴承试验台装置Fig.1　Bearing test

1.5kW的3相感应电机通过自校准联轴器与一个功率计和一个扭矩传感器相连，驱动风机进行运转。电机的负载由风机来调节。将振动加速度传感器垂直固定在感应电机输出轴支撑轴承上方机壳上进行数据采集。滚动轴承为SKF6205-2RSJEM深沟球轴承，分别在内、外圈表面用电火花加工出单点故障，其大小均为直径0.18mm，深度0.28mm。轴的旋转频率fr为29.53Hz(1 772r/min)。其对应的内圈故障频率为159.93Hz(5.415 2fr)，外圈故障频率为105.87Hz(3.584 8fr)。振动信号由加速度传感器获得，传感器用磁座安装在轴承座上。采样频率为12kHz，采样长度为8K。

图2中(a)～(d)分别为滚动轴承正常信号、内环故障信号、滚动体故障信号、外环故障信号的时域波形。4种类型信号的时域波形虽然有一定的差异,但无法通过这种非定性直观差异来区分轴承故障状态。因此，需要在研究滚动轴承故障定性差异的基础上有效提取不同故障状态差异的故障特征。

图2　4种状态轴承振动时域图Fig.2　Bearing vibration time-domain diagram of four conditions

3.2滚动轴承HHT时频谱特征

为了便于后续时频特征提取，提高计算速度，将滚动轴承的HHT时频分布划分为64个大小均等的时频网格区域，对每个区域中的时频能量幅值在时频网格中进行积分从而得到HHT时频分布棒图。不同状态下轴承HHT时频分布及时频能量分布棒图结果如图3～图6所示。

图3　轴承正常状态Fig.3　Bearing normal condition

图4　轴承内环故障状态Fig.4　Bearing inner ring fault condition

图5　轴承滚动体故障状态Fig.5　Bearings rolling element fault condition

图6　轴承外环故障状态Fig.6　Bearing outer ring fault condition

通过图3～图6中可以看出在不同的工况下，滚动轴承振动信号的HHT谱图以及其能量棒图存在着一定的差异。但HHT时频能量分布实际上是一个二维矩阵，不能直接用于判定轴承故障状态。为此在HHT能量分布差异的基础上，须做进一步的流行特征分析。

3.3滚动轴承HHT时频谱的流形特征

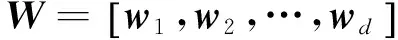
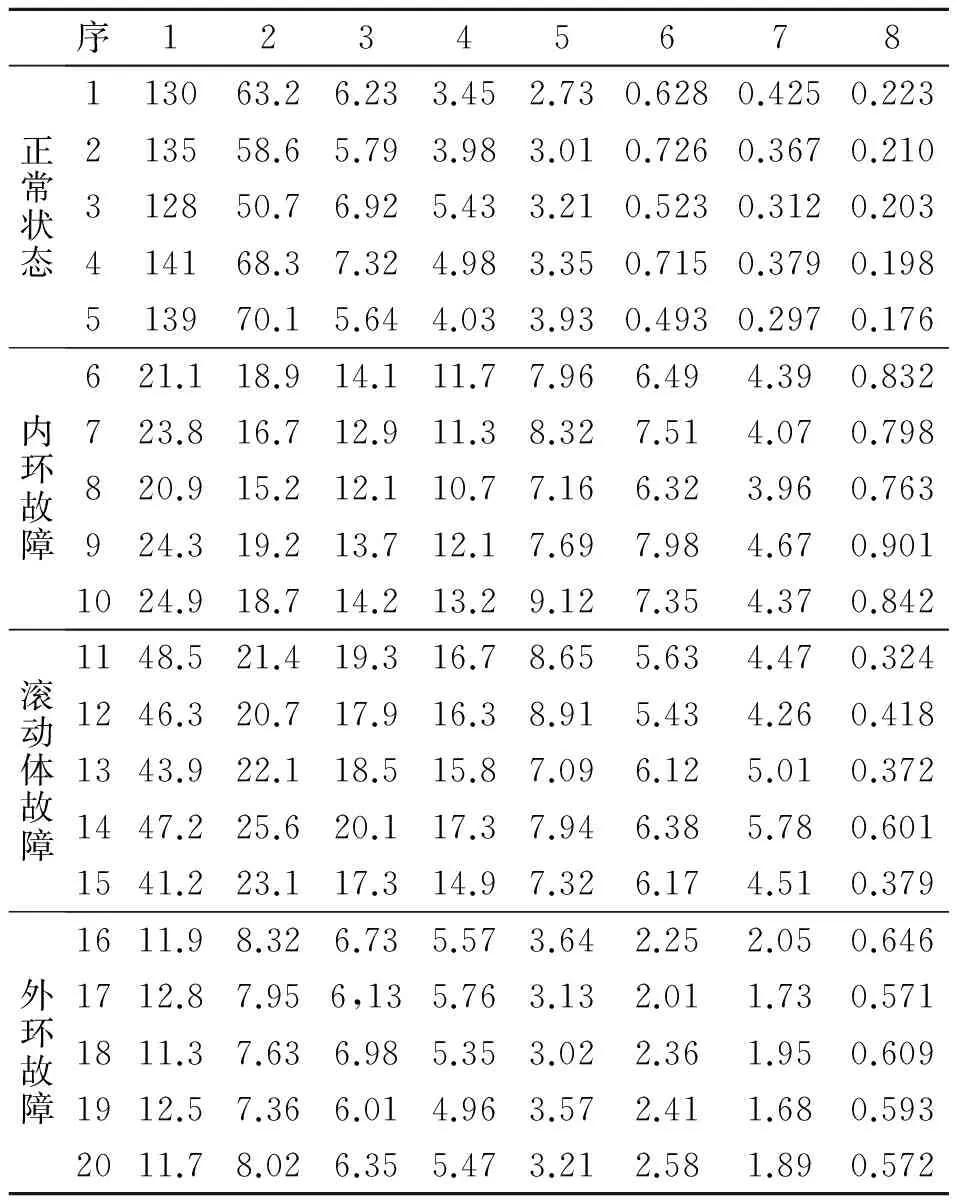
从表1看出，不同类型样本对应的奇异值具有良好的区分度，但每类轴承故障时频图的特征矩阵对应多个奇异值，需要一种更简单的定量方法对故障进行判断，为此提出一种定量衡量奇异值差异的量——奇异值熵。其定义如下：对时频图对应的特征矩阵A作奇异值分解，设奇异值为σi，σ1≥σ2≥…≥σn，则奇异谱熵定义为

(16)

表14种状态下特征矩阵的的奇异值

Tab.1Singular values of the characteristic matrix of four conditions

序12345678正常状态113063.26.233.452.730.6280.4250.223213558.65.793.983.010.7260.3670.210312850.76.925.433.210.5230.3120.203414168.37.324.983.350.7150.3790.198513970.15.644.033.930.4930.2970.176内环故障621.118.914.111.77.966.494.390.832723.816.712.911.38.327.514.070.798820.915.212.110.77.166.323.960.763924.319.213.712.17.697.984.670.9011024.918.714.213.29.127.354.370.842滚动体故障1148.521.419.316.78.655.634.470.3241246.320.717.916.38.915.434.260.4181343.922.118.515.87.096.125.010.3721447.225.620.117.37.946.385.780.6011541.223.117.314.97.326.174.510.379外环故障1611.98.326.735.573.642.252.050.6461712.87.956,135.763.132.011.730.5711811.37.636.985.353.022.361.950.6091912.57.366.014.963.572.411.680.5932011.78.026.355.473.212.581.890.572

采用轴承时频特征矩阵对应的奇异值谱熵对故障信号重新进行分类评估，计算上述各类轴承故障样本对应的奇异值谱，所得结果如图7所示。

图7　4种状态下的轴承奇异值熵Fig.7　Singular value entropy of bearing of four conditions

图7中样本1～20是正常状态下的轴承样本，其奇异值谱熵的值在4.8左右波动。21～40号样本是内环故障轴承样本，奇异值谱熵在3.2左右波动。滚动体故障的轴承样本标号为41～60，奇异值谱熵在4左右波动。61～80号样本奇异值谱熵分布在2.6左右。从中得到流形奇异值谱熵，不但考虑奇异值谱中各阶奇异值的差异，而且还可以降低特征量的维数用一个具体数值衡量多个参数的差异。

4滚动轴承故障状态分类

为了验证特征矩阵奇异值在滚动故障诊断中的效果，每种状态选20个训练样本、20个检验样本(每个样本长度为1 K)，则训练样本共有80个，检验样本共有80个。对于以上4类80个训练样本，利用上述的方法产生80个8维的特征向量。将80个奇异值特征向量利用概率神经网络进行训练分类，其结果见表2。

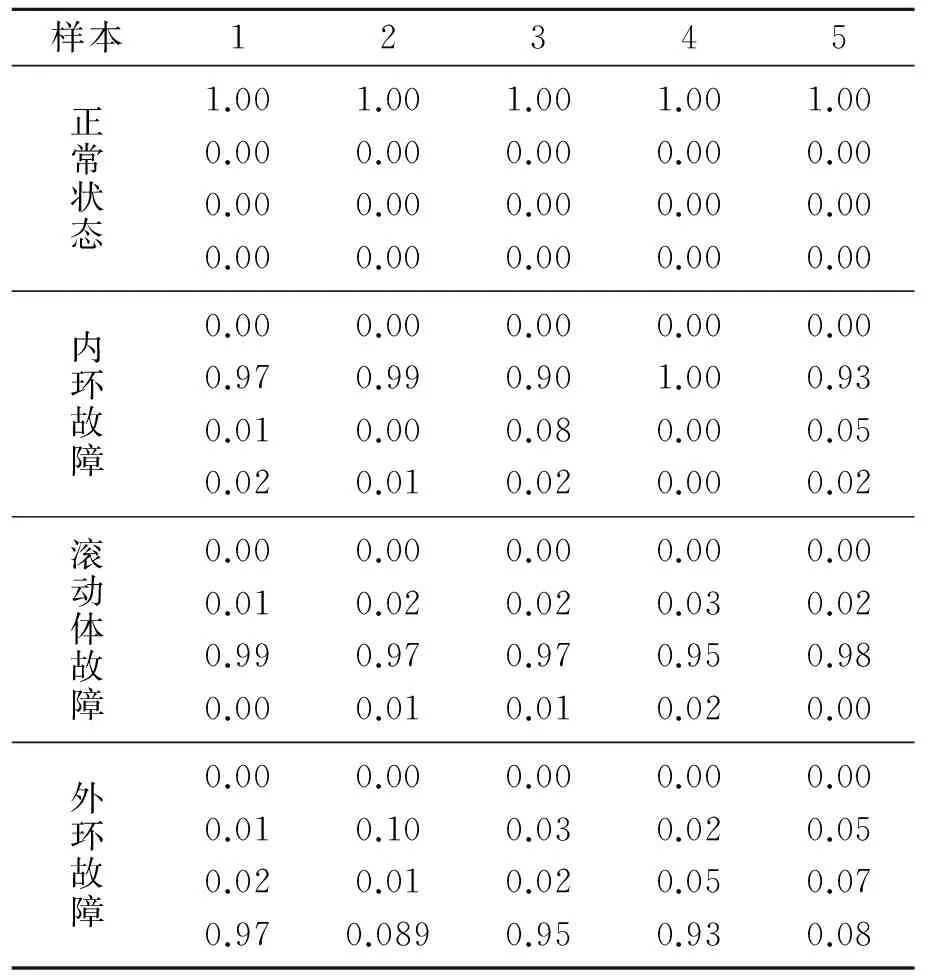
表24种状态下的轴承概率神经网络分类结果

Tab.2Classification results of four conditions of the neural network

样本12345正常状态1.000.000.000.001.000.000.000.001.000.000.000.001.000.000.000.001.000.000.000.00内环故障0.000.970.010.020.000.990.000.010.000.900.080.020.001.000.000.000.000.930.050.02滚动体故障0.000.010.990.000.000.020.970.010.000.020.970.010.000.030.950.020.000.020.980.00外环故障0.000.010.020.970.000.100.010.0890.000.030.020.950.000.020.050.930.000.050.070.08

由表2可看出，应用流形方法提取的滚动轴承时频故障特征具有较好的区分度。正常状态下的轴承分类效果最好，内环故障平均分类系数在90%以上，滚动体故障的轴承平均分类系数在95%以上，外环故障的轴承分类平均系数也可以达到90%以上。

在神经网络分类基础之上，分别计算轴承在4种工作状态下80个验证样本所对应的奇异值谱熵，结果如图8所示。

图8　4种状态下的轴承验证样本奇异值熵Fig.8　The singular value entropy of bearing is verified under four conditions

从图8中可以看出，与训练样本一样，在验证样本中不同工作状态的轴承所对应的时频图特征矩阵奇异值谱熵具有明显的区分度。由此证明，通过计算轴承HHT时频图特征矩阵的流形奇异值谱熵可以直接对轴承所属故障状态作出准确判断。

5结束语

为克服传统HHT时频特征提取方法存在的不足,去除时频特征信息的冗余,在HHT时频谱基础上提出了一种基于流形奇异值熵的滚动轴承时频故障特征提取方法。该方法应用二维流形算法有效提取代表轴承故障状态的时频投影图像。通过对时频投影图像所对应的矩阵进行奇异值分解，可以得到矩阵的奇异值向量。该向量是对投影图像矩阵特征的降维表示，在概率神经网络中的应用证明流形奇异值向量可以有效区分不同状态下的轴承故障信号。最后提出了奇异值熵特征参数概念，对滚动轴承不同故障状态进行了定量刻画和区分，为解决实际问题提供了一种有效的手段。

参考文献

[1]Ming A B, Qin Z Y, Zhang W, et al. Spectrum auto-correlation analysis and its application to fault diagnosis of rolling element bearings[J]． Mechanical Systems and Signal Processing,2013,41 (1-2):141-154.

[2]Jiang Li, Xuan Jianping, Shi Tielin. Feature extraction based on semi-supervised kernel Marginal Fisher analysis and its application in bearing fault diagnosis[J]．Mechanical Systems and Signal Processing,2013,41 (1-2):113-126.

[3]苏文胜, 王奉涛, 朱泓, 等. 基于小波包样本熵的滚动轴承故障特征提取[J]. 振动、测试与诊断,2011，31(2)：162-166.

Su Wensheng, Wang Fengtao, Zhu Hong, et al. Fault feature extraction of rolling bearing based on wavelet packet sample entropy[J]. Journal of Vibration, Measurement & Diagnosis， 2011，31(2)：162-166. (in Chinese)

[4]Peng Z K, Peter W T, Chu F L. A comparison study improved Hilbert-Huang transform and wavelet transform:application to fault diagnosis for rolling bearing[J]．Mechanical Systems and Signal Processing，2005,19(5): 974-988.

[5]Lei Yaguo, He Zhenjia, Zi Yanyang. A new approach to intelligent fault diagnosis of rotating machinery[J]．Expert System Application, 2008,35 (4):1593-1600.

[6]陈进, 姜鸣. 高阶循环统计量理论在机械故障诊断中的应用[J].振动工程学报,2001,14(2):5-14.

Chen Jin, Jiang Ming. Application of higher order cyclic statistics theory in mechanical fault diagnosis[J]. Journal of Vibration Engineering, 2001,14(2):5-14. (in Chinese)

[7]杜必强, 唐贵基, 贾子文. 振动信号扩展广义多重分形维数算法[J].振动、测试与诊断,2013,33(6):1076-1080.

Du Biqiang, Tang Guiji, Jia Ziwen. Generalized multi fractal dimension algorithm for vibration signal propagation[J]. Journal of Vibration, Measurement & Diagnosis, 2013,33(6):1076-1080. (in Chinese)

[8]赵纪元, 何正嘉, 孟庆丰. 瞬变信息提取与机器诊断[J]. 振动、测试与诊断,1993,13(4):51-59.

Zhao Jiyuan, He Zhengjia, Meng Qingfeng. Instantaneous information extraction and machine diagnosis[J]. Journal of Vibration, Measurement & Diagnosis, 1993,13(4):51-59. (in Chinese)

[9]丁康, 陈健林, 苏向荣. 平稳和非平稳振动信号的若干处理方法及发展[J]. 振动工程学报,2003,16(1):5-14.

Ding Kang, Chen Jianlin, Su Xiangrong. Processing methods and development of stationary and non-stationary vibration signals[J]. Journal of Vibration Engineering, 2003,16(1):5-14. (in Chinese)

[10]Wang Yanxue,He Zhengjia, Zi Yanyang. Enhancement of signal denoising and multiple fault signatures detecting in rotating machinery using dual-tree complex wavelet transform [J]. Mechanical Systems and Signal Processing, 2010, 24(1):119-137.

[11]Huang Norden E, Zhen Shen, Long Steven R, et al. The empirical mode decomposition and the Hilbert spectrum for nolinear and non-stationary time series analysis[J].Proceedings:Mathematical,Physical and Engineering Sciences Royal Society Lond, 1998, 454(A): 903-995.

[12]Lei Yaguo, He Zhengjia , Zi Yanyang. EEMD method and WNN for fault diagnosis of locomotive roller bearings [J]. Expert Systems with Applications, 2011, 3(6): 7334-7341.

[13]李宏坤, 周帅, 黄文宗. 基于时频图像特征提取的状态识别方法研究与应用[J]. 振动与冲击,2010,29(7):184-188.

Li Hongkun, Zhou Shuai, Huang Wenzong. Research and application of state recognition method based on time frequency image feature extraction[J]. Journal of Vibration and Shock, 2010,29(7):184-188. (in Chinese)

[14]Wang Zhiwei, Hu Changying. Shock spectra and damage boundary curves for nonlinear package cushioning system [J]. Packaging Technology and Science, 1999, 12(5): 207-217.

[15]朱利民, 牛新文, 钟秉林, 等. 振动信号短时功率谱时-二维特征提取方法及应用[J]. 振动工程学报,2004, 17(4):71-76.

Zhu Limin, Niu Xinwen, Zhong Binglin, et al. The method and application of two dimensional feature extraction of vibration signal short-time power spectrum[J]. Journal of Vibration Engineering, 2004,17(4):71-76. (in Chinese)

[16]张金玉, 张优云, 谢友柏. 时频分析方法在冲击故障早期诊断中的应用研究[J]. 振动工程学报,2000,13(2):66-72.

Zhang Jinyu, Zhang Youyun, Xie Youbo. Application of time-frequency analysis method in the early diagnosis of impact fault[J]. Journal of Vibration Engineering, 2000,13(2):66-72. (in Chinese)

[17]李宏坤, 张志新, 马小江, 等. 基于Hilbert谱熵的柴油机故障诊断方法研究[J]. 大连理工大学学报,2008,48(2):220-224.

Li Hongkun, Zhang Zhixin, Ma Xiaojiang, et al. Fault diagnosis of diesel engine based on Hilbert spectrum entropy[J]. Journal of Dalian University of Technology, 2008,48(2):220-224. (in Chinese)

[18]孙志辉. 基于Hilbert谱特征提取的智能识别方法研究与应用[D]. 大连：大连理工大学,2009.

[19]Seung H，Sebastian D, Lee D. The manifold ways of perception[J]. Science,2000,29(5500):2268-2269.

[20]Belkin M, Niyogi P, Sindhwani V. Manifold regularization:a geometric framework for learning from abeled and unlabeled examples[J]. The Journal of Machine Learning Research, 2006,7(11):2399-2434.