一种拆除机器人手臂坐标系与激光器坐标系转换方法

李　彪，岑豫皖，叶　晔，黄建中，叶金杰（.安徽工业大学机械工程学院，安徽马鞍山4300；.合肥工业大学机械与汽车学院，合肥30009）

一种拆除机器人手臂坐标系与激光器坐标系转换方法

李彪1，岑豫皖1，叶晔1，黄建中2，叶金杰1
（1.安徽工业大学机械工程学院，安徽马鞍山243002；2.合肥工业大学机械与汽车学院，合肥230009）

根据两空间直角坐标系的转换原理，简化拆除机器人坐标系与激光器坐标系的转换模型，依据简化的模型提出一种基于空间向量法的空间两直角坐标系转换方法。对激光器坐标系进行安装标定实验，通过保持两坐标系对应轴的水平限制X，Y轴的坐标旋转，通过调整激光测距仪的安装角度限制激光器坐标系绕Z轴的旋转，保证两坐标系对应轴之间相互平行。建立两坐标系转换精度测量的实验模型，依据所测数据，计算出液压锤锤尖点G1和打击点G2在两坐标系下的坐标及两坐标系中的向量和。结果表明，两向量的模基本相等，且两向量的方向偏差很小，验证了向量法进行两坐标系转换是可行的。该方法具有较高的工程适用性。

拆除机器人；向量法；激光器；坐标系转换；标定

拆除机器人［1］工作点的激光导引是通过激光标定工作点，经过多杆机械臂运动学逆解［2］求得各关节运动角度，再转换成各油缸运动行程，以此保证作业工具的精确定位。其中机器人手臂工作坐标系与激光器测量坐标系的转换是影响拆除工作精度的一个重要因素。传统的三维坐标转换采用的是七参数法［3］，其中常见的坐标转换模型主要有布尔莎模型、莫洛琴斯基模型和范式模型。但两空间坐标系之间的转换方法有多种，如张卡等［4］针对七参数法三维坐标转换问题，提出了基于罗德里格矩阵［5］的三维坐标转换方法，解决了在三维坐标转换中线性模型对旋转角大小的限制；滕志远等［6］将单位四元数法应用于坐标转换中，提出一种在求解坐标转换过程中将旋转矩阵和平移向量转化为求解多元函数极小值的方法，直接解出坐标转换的旋转矩阵和平移向量。但是上述方法在使用的过程中都需繁杂的运算和复杂的坐标标定［7］。

空间向量法原理简单，不需对每个坐标轴进行复杂的标定和运算，所得结果能够满足实验要求。目前将向量法应用于空间三维坐标系转换的研究所见报道较少。鉴于此，笔者提出一种基于空间向量法的拆除机器人手臂坐标系和激光器坐标系转换方法，为后续对机器人手臂坐标系转换的研究提供参考。

1　坐标系转换的一般原理

针对机器人激光导引工作情况，设两空间直角坐标系分别为机器人手臂坐标系O-XYZ和激光器坐标系O1-X1Y1Z1，其中激光器测量出机器人工作点在O1-X1Y1Z1的坐标，通过坐标空间位置和姿态变换求出其在O-XYZ的坐标，通过机械臂运动学方程求出各关节角，实现对工作点的控制。不失一般性设2个空间直角坐标系对应坐标轴之间不平行，且两坐标系的原点不重合［8］。设O-XYZ为固定坐标系，O1-X1Y1Z1相对于坐标系 O-XYZ的平移参数（Δx，Δy，Δz），欧拉角γ，β，α为3个旋转参数，是分别绕X，Y，Z轴旋转的角度［9］。设空间任意一点P在机器人手臂坐标系O-XYZ中的坐标为P（x，y，z），在激光器坐标系O1-X1Y1Z1中的坐标为P1（x1，y1，z1），如图1。

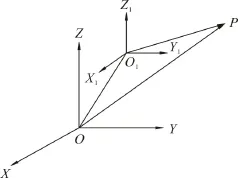
图1　机器人手臂坐标系与激光器坐标系Fig.1 Robot arm coordinate system and laser coordinate system

P与P1点坐标转换可表示为

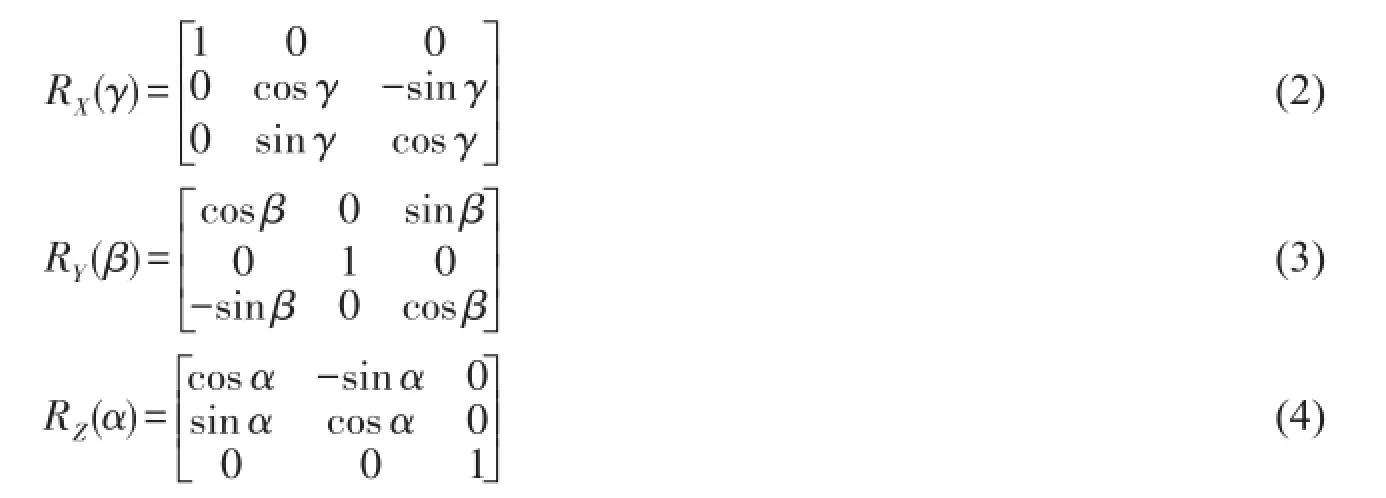
式（1）表明物体在空间的位置和姿态变换可用6个自由度来描述，即3个方向的平移运动和绕3个方向轴的旋转运动［10］。根据式（1）可知，两空间直角坐标系的转换需进行矩阵计算，为了验证两空间直角两坐标系转换的精度，需对坐标系进行较为复杂的标定实验。为此，对两空间直角坐标系转换的模型进行简化处理。

设机器人手臂坐标系和激光器坐标系中对应轴相互平行，则P与P1点坐标转换可表示为

运用式（5）需知两空间直角坐标系之间的平移参数［11］，但激光器坐标系相对拆除机器人手臂坐标系的平移参数很难直接通过测量的方法得到，为此提出基于空间向量法的空间两直角坐标系转换方法。

2　拆除机器人手臂坐标系与激光器坐标系转换的向量法

图2　向量法求解未知点PFig.2 Vector method for solving the unknown point P

已知拆除机器人当前手臂末端锤尖点位置P1，P1点在机器人手臂坐标系下的坐标为P1（x1，y1，z1），在激光器坐标系下的坐标为设未知点P在机器人手臂坐标系下的坐标为P（x，y，z），在激光器坐标系下的坐标为运用向量法求解未知点P在机器人手臂坐标系下的坐标P（x，y，z）。如图2。

则可得

这种方法不需精确的坐标标定和复杂的计算，只要求激光测距仪有一定的空间测量精度。同时该方法不限制激光器的安装位置，其在激光测距仪的使用范围内即可。为保证两空间坐标系相互平行，可通过调整机械臂的安装平台和激光测距仪的安装平台实现。在某些情况下，如果不能保证Z轴的旋转，手臂末端锤尖点位置可以通过下式计算求得

3　激光器坐标系与拆除机器人手臂坐标系转换实验

3.1激光器坐标系的安装标定实验

为保证机器人手臂坐标系与激光器坐标系转换的精确性，对激光器的安装进行标定实验。其方法是：调整激光测距仪的安装平台，使2个坐标系相对应轴之间保持水平以限制X，Y轴的坐标旋转，调节激光测距仪的安装角度限制激光器坐标系绕Z轴的旋转。

图3　XOY面与水平面平行的标定调整模型Fig.3 Parallel calibration adjustment model between the XOY plane and the horizontal plane

1）限制X，Y轴的坐标旋转

限制X，Y轴坐标旋转的标定实验模型如图3。依图3所示的模型搭建实验平台，连接云台和支架，将云台和支架安装在拆除机器人的机身上。将带有刻度的挡板垂直水平面放置，并保证挡板到云台的距离在拆除机器人手臂工作范围之外。启动云台激光器系统，控制云台水平转动任一个角度，再调整挡板位置，使激光器光束打在刻度挡板的中心位置O点，同时使用手持式激光测距仪测量刻度挡板上C点和D点到地面的垂直距离，调整挡板保证C点和D点到地面的垂直距离相等，然后将挡板固定。

通过云台控制界面调节云台水平转动的速度（200步/s），使云台在水平方向上缓慢平稳地转动，每次转动为100步。分别控制云台从O点向C点和D点转动，并记录每转动100步时激光光斑打在挡板上的位置，再微调云台激光器系统安装在支架上的4个支脚点的高度，直至激光光束打在挡板上的光斑与直线CD重合。同样在垂直方向的直线AB上进行相同实验。

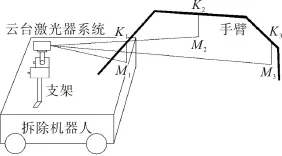
图4　限制Z轴旋转的模型Fig.4 Model of limiting Z axis rotation

2）限制绕Z轴的旋转

为限制激光器坐标系绕Z轴的旋转，设计标定方案，根据设定方案建立模型，如图4。

由图4所示模型搭建实验平台，通过云台控制界面使云台回到零点位置，同时控制拆除机器人手臂的水平转动，使手臂回到原点位置。在拆除机器人手臂上选取水平间隔相等的3个点，即K1，K2和K3，在此3点放置3块挡板，并保证3块挡板垂直于手臂和地面，通过K1，K2和K3点沿着相对应的挡板画3条水平线。控制云台俯仰方向运动，使激光光束分别与3块挡板上的直线相交，并记录相交点的位置，即M1，M2和M3点。使用手持式激光测距仪测量M1K1，M2K2和M3K3的长度，微调云台激光器平台水平方向的旋转，直至M1K1，M2K2和M3K3的长度相等，再固定云台激光器平台，进而限制激光器坐标系绕Z轴的旋转。

通过以上2个安装标定实验可以保证激光器坐标系与拆除机器人坐标系对应轴相互平行，完成激光器坐标系的安装标定。

3.2两坐标系转换实验

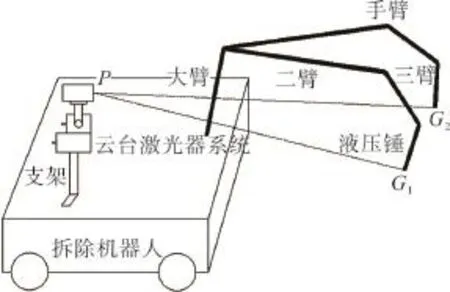
图5　两坐标系转换精度测量模型Fig.5 Two coordinate transformation precision measurement model

两坐标系转换精度测量实验模型如图5，根据图5的模型搭建实验平台。启动拆除机器人，通过遥控手柄控制拆除机器人手臂运动。控制大臂油缸和三臂油缸伸长量为零，转锤油缸伸长量为L锤，再通过控制二臂油缸使液压锤的锤尖到达一定位置。控制云台转动，使激光器光斑打在锤尖G1点位置，读取此时云台水平转动角度θ平1、俯仰转动角度θ俯1和激光测距仪显示数据PG1，同时测量二臂油缸伸长长度L21。控制二臂油缸使液压锤的锤尖慢慢抬起到G2点位置，再控制云台转动，使激光器光斑打在锤尖G2点位置。读取此时云台水平转动角度θ平2、俯仰转动角度θ俯2和激光测距仪显示数据PG2，再测量二臂油缸伸长长度L22。

实验测PG1=2 977mm，θ平1=-8.385∘，θ俯1=-31.089∘；PG2=2 912 mm，θ平2=-7.816∘，θ俯2=-20.846∘。根据测得的数据可求出G1和G2点的坐标，G1（2 522.15，-371.76，-1 537.23），G2（2 696.10，-370.52，-1 036.26）。

已知各手臂油缸的伸长量，根据拆除机器人手臂正运动学求解方法可以求出和的坐标，臂油缸伸长量的测量值为L锤=78 mm，L21=168 mm，L22=264 mm。根据油缸伸长量可以求出和点的坐标，（1 807.08，0，-71.82），（1978.2，0，431.6）。

由以上分析可知，两向量的模基本相等，两向量对应项相除所得数值基本相等，即两向量的方向偏差很小，两向量基本相等。由此表明，使用空间向量法进行云台激光器坐标系与拆除机器人坐标系的转换是可行的。

4　结　论

坐标系转换在工程中应用十分广泛，为省去繁杂计算过程和复杂的坐标标定，通过简化拆除机器人坐标系和激光器坐标系转换的模型，使用向量法实现两坐标系之间的转换，转换过程中需对激光器坐标系进行简单的坐标标定，通过实验验证两坐标系转换的可行性。结果表明，使用向量法进行云台激光器坐标系与拆除机器人坐标系转换是可行的。

［1］王玉飞，岑豫皖，包家汉，等.拆除机器人结构的动态有限元分析［J］.安徽工业大学学报（自然科学版），2008，25（4）:403-407.

［2］陈鹏，刘璐，余飞，等.一种仿人机械臂的运动学逆解的几何求解方法［J］.机器人，2012，34（2）:211-216.

［3］卢忠，归友龙，刘勇.基于总体最小二乘法的三维坐标转换参数解算［J］.山西建筑，2009，35（36）:359-360.

［4］张卡，张道俊，盛业华，等.三维坐标转换的两种方法及其比较研究［J］.数学的实践与认识，2008，38（23）:121-128.

［5］原玉磊，蒋理兴，刘灵杰.罗德里格矩阵在坐标系转换中的应用［J］.测绘科学，2010，35（2）:178-179.

［6］滕志远，张爱武.单位四元数法在激光点云坐标转换中的应用［J］.测绘通报，2010（11）:7-10.

［7］戴美玲，杨福俊，代祥俊，等.一种基于双参考平面的等相位坐标标定方法［J］.光学学报，2014，34（5）:0512006.

［8］汪生燕，王海芹.浅谈WGS-84坐标系与任意坐标系的坐标转换［J］.西部探矿工程，2009（4）:148-150.

［9］陈泽恩.浅谈矩阵代数在计算机图形学上的应用［J］.惠州大学学报，2001，21（4）:150-154.

［10］姜广文，晁志超，伏思华，等.基于单摄像机的物体位置和姿态变形测量研究［J］.光电子·激光，2009，20（6）:775-777.

［11］朱彦鹏，谭坚贞，穆宇亮，等.钢筋混凝土框架结构平移参数计算［J］.工程抗震与加固改造，2008，30（3）:5-9.

责任编辑：何莉

AConversion Method BetweenArm Coordinate System and Laser Coordinate System for Demolition Robot

LI Biao1，CEN Yuwan1，YE Ye1，HUANG Jianzhong2，YE Jinjie1
（1.School of Mechanical Engineering，Anhui University of Technology，Ma'anshan 243032；2.School of Mechanical andAutomotive Engineering，Hefei University of Technology，Hefei 230009）

According to the conversion principle for two space rectangular coordinates，a conversion model was simplified between the robot coordinate system and the laser coordinate system.On the basis of the simplified model，amethodfortransformingtwospacerightanglecoordinateswasproposedbasedonthespacevectoralgorithm. An installation and calibration experiment of the laser coordinate system was performed.By maintaining the level of the corresponding axes of the two coordinates，the coordinate rotation of X and Y axes were limited.Moreover，through adjusting the installation angle of the laser range finder，the rotation around Z axis was limited so as to ensure the corresponding two axes are parallel to each other.An experimental model of conversion measurement accuracy of the two coordinate systems was established.Based on the measured data，the coordinates ofG1point， representing the hydraulic hammer’s hammerpick，and the strike pointG2，and the vectors ofandwere calculated in the two coordinate systems.The results show that norms of the two vectors are substantially equal，and the deviation of directivity of the two vectors is small.It is verified that the vector method for transforming the two coordinate systems is feasible，the method has a good applicability in engineering.

demolition robot；vector method；laser device；transformation of coordinates；calibration

TP242.3

A

10.3969/j.issn.1671-7872.2016.01.011

1671-7872（2016）-01-0049-05

2015-04-23

安徽省科技攻关计划项目（1301022091）；安徽省优秀青年人才基金重点项目（2013SQRL023ZD）；安徽工业大学青年教师科研基金项目（QZ201311）

李彪（1988-），男，安徽阜阳人，硕士生，主要研究方向为基于激光导引的拆除机器人手臂位置控制。

岑豫皖（1951-），男，河南杞县人，教授，主要研究方向为机器人技术、机电液系统与产品设计等。