岩块的弹性模量及岩体单位弹性抗力系数的确定方法
2016-08-02菊存全
菊存全
(中国水利水电第十四工程局有限公司勘察设计研究院,昆明 650051)
岩块的弹性模量及岩体单位弹性抗力系数的确定方法
菊存全
(中国水利水电第十四工程局有限公司勘察设计研究院,昆明 650051)
通过岩体变形模量与岩块弹性模量之间关系,根据岩石的软硬程度,按层状结构和非层状结构,运用岩体完整性系数作为媒介反求岩块的弹性模量,最终运用H oek-D i ederi chs方程求解岩体的变形模量。弹塑性理论法、坚固性系数法在相同的计算条件下,求解单位弹性抗力系数结果基本一致,其中,有限元模型弹塑性理论法更具适用性。
H oek-D i ederi chs方程;弹性模量;变形模量;完整性系数;弹性抗力系数;泊松比;软化系数;折减系数
1 引言
通过对《水利水电工程地质勘察规范》(GB 50487—2008)附录V坝基岩体工程地质分类及表E.0.4变形参数经验值对应关系之间关系,通过研究分析,运用数学方法拟合出岩体变形模量与岩体完整性系数之间的关系式,进而运用岩块弹性模量Ei与岩体的变形模量Em关系之间的关系反求Hoek-Diederichs方程中的岩块弹性模量,以便在霍克布朗强度准则条件下运用Hoek-Diederichs方程,最终运用弹塑性理论法求解地下洞室围岩的单位弹性抗力系数。
2 岩块弹性模量Ei与岩体的变形模量Em关系
Hoek-Diederichs方程[1]为:

式中,Ei为完整岩石的弹性模量,MPa;De为开挖扰动系数;GSI为地质强度指标。
根据前人研究资料[2,3]及《水利水电工程地质勘察规范》(GB 50487—2008)附录V坝基岩体工程地质分类及表E.0.4变形参数经验值对应关系,研究结果表明,岩体的弹性模量并非与岩块的弹性模量正比于岩体的完整性系数Kv,其关系如下:

根据《水利水电工程地质勘察规范》(GB 50487—2008)附录V坝基岩体工程地质分类表与表E.0.4变形参数经验值对应关系,研究结果表明,岩体的完整性系数Kv与岩体变形模量Ep(GPa)之间的关系如表1。

表1 变形模量Ep与完整性系数Kv之间的关系
根据式(2)及表1可得岩块弹性模量与岩体完整性系数之间的关系(见表2):

表2 弹性模量Ei与完整性系数Kv之间的关系
根据工程实际情况,将表2中相应岩块弹性模量代入式(1),即可求得Hoek-Brown强度准则条件下岩体的变形模量Em,对软质岩不需要根据岩石软化系数进行折减,但应用时应注意,对层状结构岩体,当岩体的完整性系数Kv<0.35时,仍按非层状结构岩体考虑。
3 变形模量求解比较
通过对《中小型水力发电工程地质勘察规范》(DLT 5410—2009)、《水电水利工程地下建筑物工程地质勘察技术规程》(DLT5415—2009)、《水利水电工程地质勘察规范》(GB50487—2008)和《工程岩体分级标准》(GBT 50218— 2014)隧洞、坝基、地基及边坡各种分类方法对应下所给的岩体变形模量值基本相同,其中,前三种规范对应的分类级别下岩体的变形模量完全相同。说明表1、表2方法所求变形模量、弹性模量具有普遍性,适用于各类岩体工程,也说明通过本文方法运用Hoek-Diederichs方程求解岩体的变形模量Em也具有普遍性。
4 岩体单位弹性抗力系数的确定
4.1 弹塑性理论法
由于岩体变形模量的求解方法不同,通过与规范的坚固性系数法在不同的求解条件下,计算分析研究比较,总结出了规范法的弹塑性理论法和弹塑性理论法之有限元模型法如下:
1)规范弹塑性理论法

2)有限元模型弹塑性理论法

式中,μm为岩体的泊松比;Em为岩体的弹性(变形)模量,MPa;Kv为岩体的完整性系数;δ为各向异性系数或折减系数,δ可按下列公式求解:

公式中岩体的泊松μm比可按下列方法确定:
对于硬质岩,

对于软质岩,可按下式[4,5]确定

式中,φm为岩体的抗剪断内摩擦角,(°);De为岩体的开挖扰动系数;Em为岩体的变形模量。
上述求解岩体弹性抗力系数时应注意,在求解岩体的的弹性(变形)模量Em时,对层状结构岩体,当岩体的完整性系数Kv<0.35时,均按非层状结构岩体考虑。从式中可以看出,规范弹塑性理论法求解岩体的单位弹性抗力系数,当完整性系数Kv≥0.35时应乘以各向异性系数δ,当完整性系数Kv<0.35时,不需要乘以各向异性系数δ,符合较破碎、破碎的岩体可视为均质各向同性岩体的说法。有限元模型弹塑性理论法,则不需乘以各向异性系数δ,符合有限元计算模型理论。
4.2 坚固性系数法
根据工程试验数据及工程实践检验,结合《水电水利工程地下建筑物工程地质勘察技术规程》(DLT5415—2009)表k.1各类围岩主要物理力学参数经验取值,总结出了岩体的单位弹性抗力系数K0与岩体的坚固性系数f有如下经验关系:
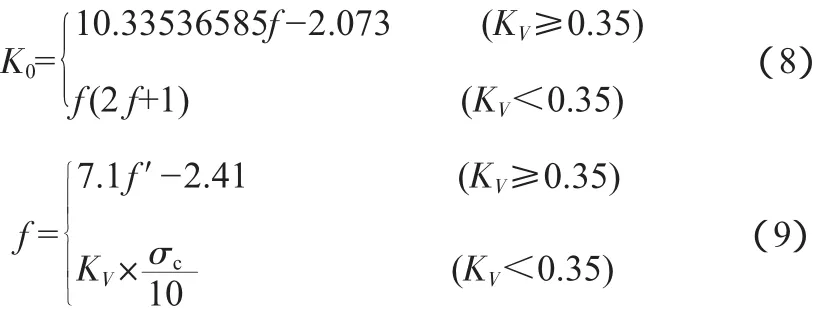
式中,f′为岩体的抗剪断摩系数;Kv为岩体的完整性系数;σc为岩块的单轴饱和抗压强度标准值。
5 单位弹性抗力系数的求解比较
通过计算比较(见表3、表4)发现,霍克布朗强度准则条件下与规范法比较,弹塑性理论法虽有差异,但十分接近,说明运用Hoek-Diederichs方程和规范法求解岩体的变形模量基本是一致的。坚固性系数法,对软质岩,两种条件下计算的单位弹性抗力系数有些悬殊,似乎霍克布朗强度准则条件下的计算结果偏大,其原因有:①计算的环境条件不同;②霍克布朗强度准则条件下求解的抗剪断摩擦系数大于规范法求解的抗剪断摩擦角。在不同的求解环境下,有限元计算模型理论方法求解结果虽有差异,但悬殊不大,说明有限元模型法更具适用性。

表3 霍克布朗强度准则条件下,岩体弹性抗力系数计算结果比较
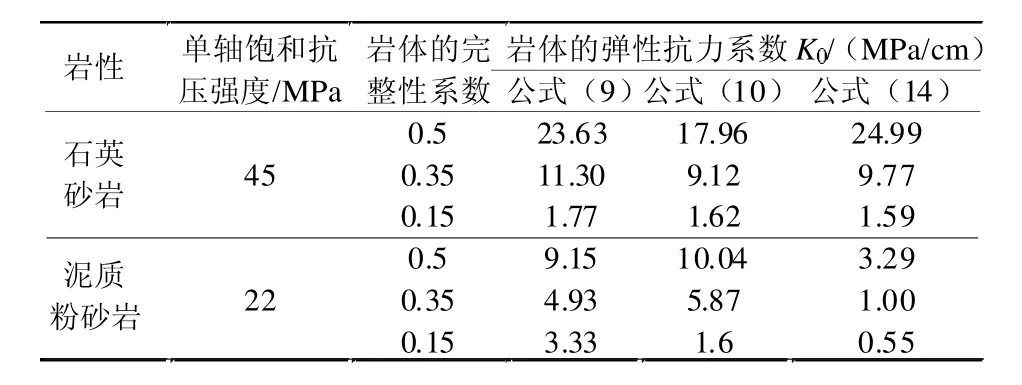
表4 规范法计算岩体弹性抗力系数计算结果比较
6 结语
1)运用岩体的完整性系数Kv作为媒介求取岩体的变形模量、岩块的弹性模量是确实可行的。岩体的弹性模量并非与岩块的弹性模量正比于岩体的完整性系数Kv。在工程实际运用时,应根据不同的地质情况选择不同的变形模量、弹性模量公式求解。
2)根据Hoek-Diederichs方程和规范经验公式所求变形模量、弹性模量均具有普遍性,适用于各类岩体工程。应用规范经验公式计算岩体的变形模量时,对于软质岩应根据岩石软化系数进行折减,而应用Hoek-Diederichs方程计算岩体的变形模量时,则不需进行折减。
3)无论是运用规范经验公式还是运用Hoek-Diederichs方程求解岩体的变形模量时,对层状结构岩体,当岩体的完整性系数Kv<0.35时,均应按非层状结构岩体考虑。在求解岩体的弹性抗力系数、泊松比时,应按岩体的软硬程度选择适宜的计算公式。
4)弹塑性理论法、坚固性系数法求解地下洞室围岩单位弹性抗力系数均是可行的,其中有限元模型弹塑性理论法,在求解地下洞室围岩的单位弹性抗力系数方面更具合理性。
【1】E.Hoek.MS.Diederichs.EnpiricalestinationofrockMassDodulus[J]. InterdationalJournalofRockMechaoics&M iningSciences,2006(43): 203-215.
【2】郭强,葛修润,车爱兰.岩体完整性指数与弹性模量之间的关系研究[J].岩石力学与工程学报,2011(S2):3914-3919.
【3】王亮清,唐辉明,夏元友,等.不同风化程度岩体弹性模量的确定方法研究[J].金属矿山,2008(7):19-21.
【4】汤大明,曾纪全,胡应德,陈梦德.关于泊松比的试验和取值讨论[J].岩石力学与工程学报,2001(S1):1772-1775.
【5】张年学,盛祝平,李晓,李守定,赫建明.岩石泊松比与内摩擦角的关系研究[J].岩石力学与工程学报,2011(S1):2599-2609.
Determ ination Method of ElasticModulus of Rock Mass and Elastic Resistance Coefficient of RockMass Unit
JUCun-quan
(SinohydroBureau14 Co.Ltd,Kunming 650051,China)
Through the rock deformation modulus and rock elastic modulus relationship between,according to the degree of soft rock, according to the layered andnon layered structure,using integrity factorof rockmassasamedium reverse rockelasticmodulus,theultimate useofHoek-Diederichsequationofrockmassdeformationmodulus.Underthesameconditions,theresultsofelastic resistancecoefficientof elasticand plastic theoryand strongcoefficientmethodarebasically thesame,and the finiteelementmodelismoresuitable forelasticplastic theory.
Hoek-Diederichs equation;elastic modulus;deformation modulus;integrity coefficient;elastic resistance coefficient;Poisson'sratio;softeningcoefficient;reduction factor
TV311;O312
A
1007-9467(2016)08-0058-03
10.13616/j.cnki.gcjsysj.2016.08.011
2016-01-13
菊存全(1973~),男,云南曲靖人,高级工程师,从事岩体力学参数取值研究,(电子信箱)543800337@qq.com。
