基于均值化主成分分析的城镇居民消费性支出应用研究
2016-08-02陈江丽
陈江丽
基于均值化主成分分析的城镇居民消费性支出应用研究
陈江丽
(滇西科技师范学院信息科学与技术系,云南临沧677000)
均值化主成分分析是在传统主成分分析法的基础上,采用均值化方法对数据进行预处理的一种改进方法。利用均值化主成分分析法对全国各地区城镇居民的人均消费支出情况进行分析,并使用Matlab平台进行仿真,最终提取出反映消费支出的主成分,为下一步的研究工作提供必要的决策支持。
均值化;主成分分析;城镇居民;人均消费性支出;指标体系
0 引言
主成分分析(PCA)是一种线性降维技术,它可以将原来的变量重新组合成一组新的相互无关的综合变量,即主成分,并从中提取出几个较少的主成分,但却能反映原始变量的大部分信息。这种处理方式能简化数据结构,尽可能多地反映原始评价因子的信息,其有利于抓住事物的主要矛盾,使问题得到简化。
主成分分析的功能有:降低指标的维数、去除指标之间的相关性和解释样本信息。其中,主成分分析主要应用于研究变量相关性的问题。
传统的主成分分析从协方差矩阵出发求解主成分,而协方差矩阵易受指标的量纲和数量级的影响。因此,一般对原始数据进行标准化处理[1]。标准化处理会使协方差矩阵变成相关系数矩阵,由于原始指标中主要包含两部分信息:由方差大小反映的各指标的变异程度信息和由相关系数矩阵来体现的各指标间相互影响信息。利用传统主成分分析法对数据进行标准化处理,会使各指标的方差变为1,只去除了各指标变异程度上的差异,却不能准确反映原始数据所包含的全部信息[2-4]。标准化数据处理方法虽然消除了量纲和数量级的差异,但也去除了各指标变异程度上的差异,造成了信息的丢失[5]。因此,必须对原始数据的标准化处理方法进行改进。本文利用均值化方法改进传统主成分分析方法。
1 均值化主成分分析方法
通过在传统主成分分析方法的数据预处理环节采用均值化方法对原始数据进行处理,进一步提高分析结果的准确性。若存在n个样本组成的样本集X,每个样本有p个指标,则第i个样本Xi=(Xi1,Xi2,…,Xip),i=1,2,…,n。对Xi样本进行均值化的方法如下:
将原始样本数据Xi与各指标的均值的比值作为新的样本数据zi。则均值化后的第i个样本的第j个指标的数值zij由公式(1)计算得出:
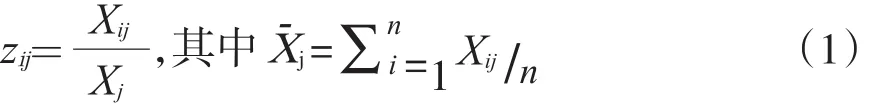
于是均值化后的第j个指标的均值
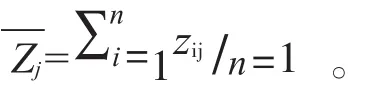
因此,均值化数据预处理方法即满足了标准化处理的要求,又充分考虑了各指标间的差异,全面反映了数据的全部信息,能有效地解决标准化处理方法存在的弊端。
2 利用均值化主成分分析法研究城镇居民的消费支出情况
近年来,随着国家经济和社会的飞速发展,人民生活水平的不断提高,城镇居民的消费水平也在日益增长,消费结构发生了显著变化。居民的消费增长直接关系到整个国民经济增长的速度和质量,然而影响居民消费增长的因素主要体现在:城镇居民的平均消费支出水平、各类消费在消费总支出中所占的比重和消费结构的变化等方面。其中,消费结构的研究对扩大内需、搞活社会主义市场经济、制定产业政策、促进国民经济的发展都有着极其重要的影响[6]。
由于国内各地区的经济发展不平衡,居民的消费水平和消费性支出也存在着很大的差异。因此,对我国各地区城镇居民人均消费性支出的各项指标进行统计分析,综合出全面反映居民消费情况的主要因素,简化其它的次要因素,为进一步研究城镇居民的消费性支出水平和消费结构的差异提供主要的参考证据。
2.1 建立城镇居民人均消费性支出指标体系
分析和研究城镇居民消费性支出水平,必须构建合理的指标体系。构建指标体系必须遵循全面性、整合性、代表性和可操作原则。遵循上述原则,本文建立的城镇居民人均消费型支出指标体系如表1所示。该体系中包含八项反映城镇居民消费结构和消费水平的指征,能全面反映居民的消费情况,都是日常生活中比较有代表性的消费行为。另外,结合该指标体系,可以将2012年地区城镇居民人均生活消费支出(来源于《中国统计年鉴2012》)数据作为研究样本,数据来源真实并具有权威性。

表1 城镇居民人均消费性支出指标体系
2.2 利用均值化主成分分析法对城镇居民的消费支出情况进行matlab仿真并分析
2.2.1 对均值化后的样本数据作主成分分析
在Matlab平台中,对均值化后的各地区城镇居民人均消费支出样本数据,利用princomp函数进行主成分分析,输出主成分表达式的系数矩阵Coeff、主成分得分数据Score、样本相关系数矩阵的特征值向量latent。利用这些运行结果,可以作进一步的分析和研究。
根据样本相关系数矩阵的特征值latent,通过计算特征值和所有特征值总和的比值得出各主成分的贡献率Explained。
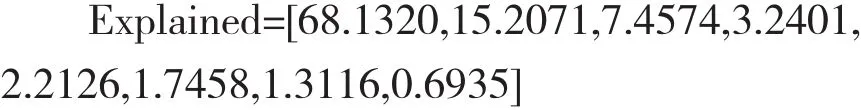
通过出前2个主成分的累积贡献率已达到了83.3391%,后面6个主成分的贡献率非常小。因此,只需选取前两个主成分作为代表,并作进一步地分析。
结合主成分表达式的系数矩阵Coeff,写出前2个主成分的表达式如下:
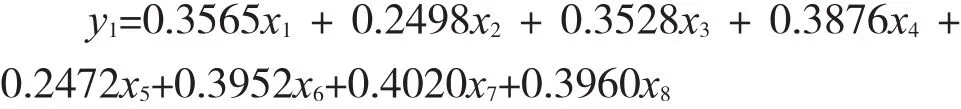
2.2.2 第一主成分分析
从第一主成分y1的表达式可以看出,每个指标变量都有相近的正载荷,说明每个指标对第一主成分的影响基本相当。因此,将均值化后各地区的各消费指标数据汇总求和计算出消费总支出,并按第一主成分的得分数据Score由低到高进行排序,结果如图1所示。可以看出,每个地区的消费总支出和第一主成分得分数据都基本成正比。因此,第一主成分反映的是城镇居民人均消费支出的综合水平,可将第一主成分作为综合消费支出成分。
2.2.3 第二主成分分析
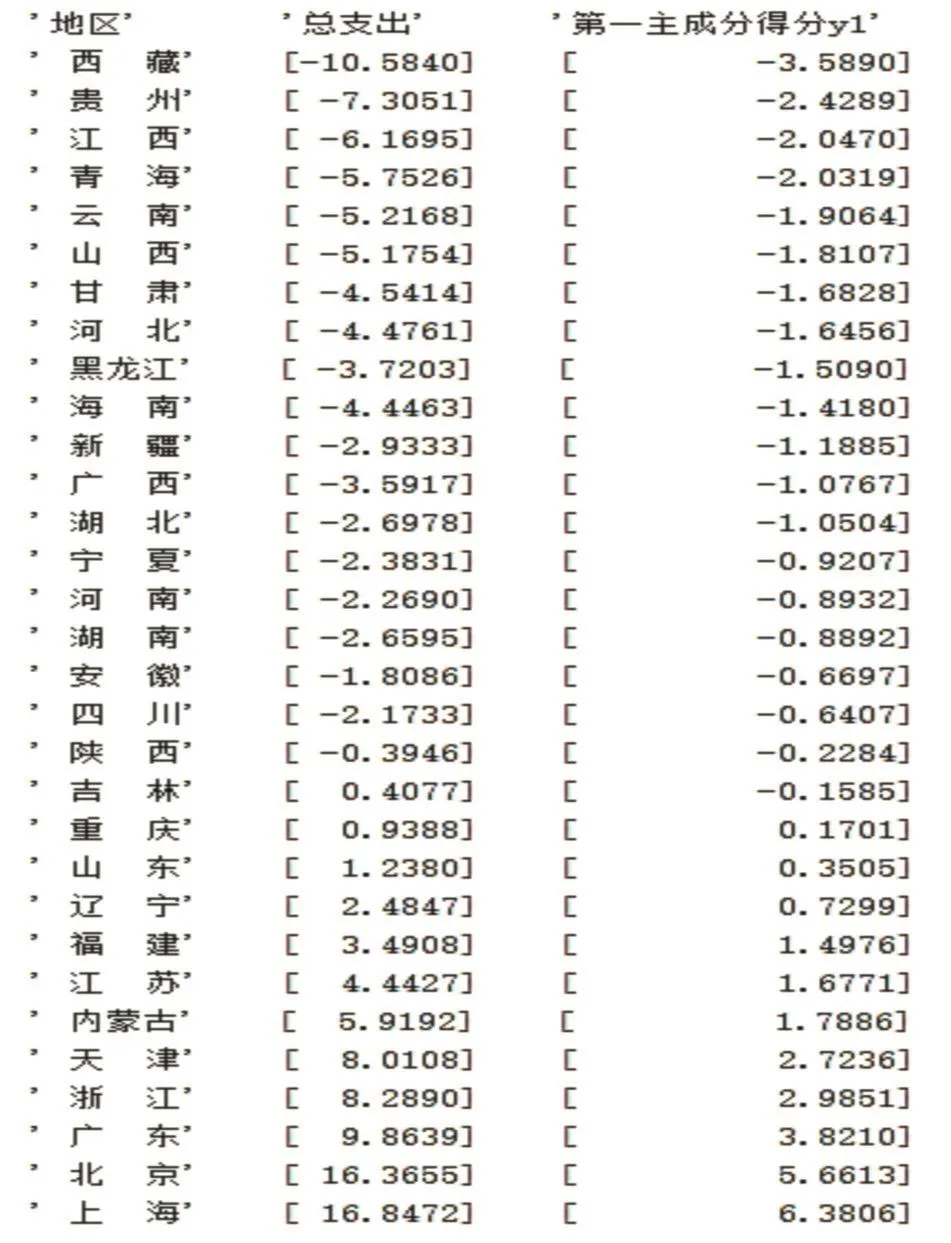
图1 各地区消费总支出及第一主成分的得分数据
从第二主成分的表达式可以看出,指标(衣着)和(医疗保健)有中等程度的正载荷,指标(食品)和(交通和通信)有中等程度的负载荷,说明反映的是衣着和医疗保健的消费总支出、食品和交通通信消费总支出两个方面的对比。因此,计算出均值化后各地区两个方面消费总支出之差,并按第二主成分的得分数据Score由低到高进行排序,结果如图2所示。两个方面消费支出之差与第二主成分得分基本成正比,通过比较发现,从地区所处的地理位置可以看出,南方地区如上海、广东、福建、海南等在食品和交通通信方面的消费支出比较大,而北方地区如辽宁、黑龙江、吉林和内蒙古等在衣着和医疗方面的消费支出比较大。主要原因跟南北方的气候差异有关,北方地区天气寒冷,居民的消费倾向于购买衣着和支付医疗保健费用。而南方气候温和,适宜外出活动,居民的消费则倾向于食品和交通通信方面。因此,第二主成分可作为倾向消费支出成分。
2.2.4 分析结果检验
为了分析只提取前两个主成分而丢掉后面的主成分会造成的信息损失,可调用pcares函数,由主成分得分数据Score重建样本观测数据,计算相对误差均方根E。
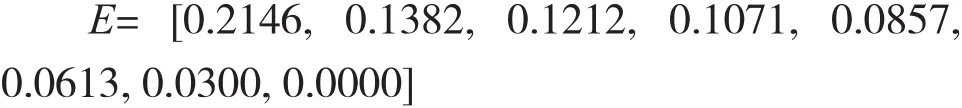
从结果可以看出,当使用前两个主成分重建观测矩阵时,相对误差的值都有所下降,随着主成分个数增多,相对误差稳步下降,当使用全部主成分时,相对误差为0,表示没有信息损失。
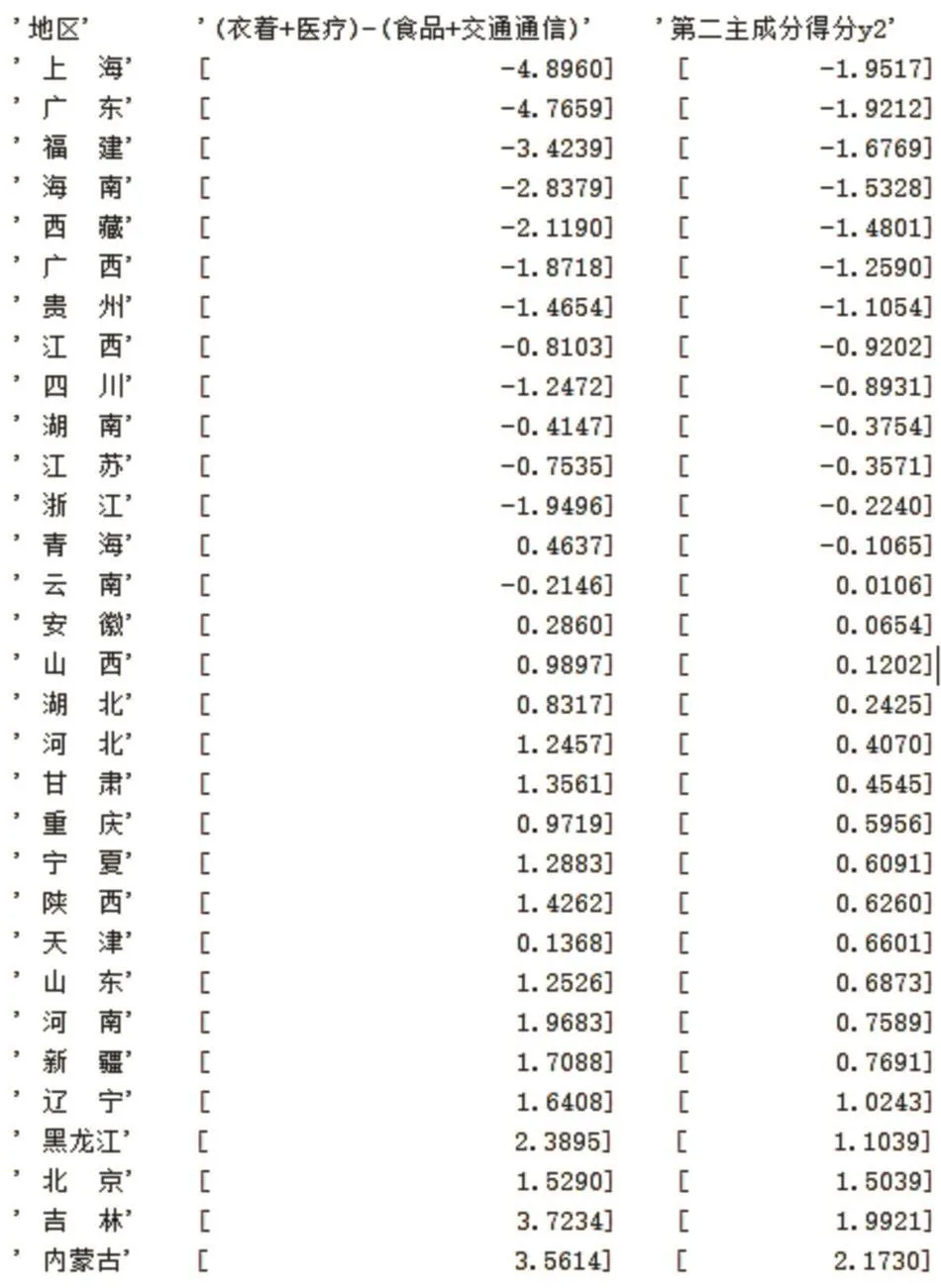
图2 两个方面消费支出之差及第二主成分的得分数据

图3 各地区两个主成分得分散点图
2.3 综合分析
为了全面反映地区间两个主成分的得分情况,作出如图3中所示的两个主成分得分散点图。从图3中可以看出,总消费较高的地区如上海、北京、广东和浙江等,第一主成分得分较高;总消费较低的地区如西藏、贵州、江西等,第一主成分得分较低,说明第一主成分反映了综合消费水平的高低。另外,北方地区第二主成分的得分较高,中部地区次之,南方地区得分较低,则说明第二主成分是由地域差异造成的消费倾向成分。
另外,根据图3中反映的各地区两个主成分得分情况,可以按居民人均消费支出情况将全国31个省、市、自治区和直辖市划分为3类:第一类为上海、北京、广东;第二类为西藏、贵州;其余地区为第三类。
3 结语
利用均值化主成分分析法对城镇居民人均消费支出情况进行分析,能提高结果的准确性,提取出全面反映消费支出情况的主成分,对进一步研究影响消费的因素提供科学和全面的参考依据,为研究对策和经济政策的制定提供决策支持。
[1]纪荣芳.主成分分析法中数据预处理方法的改进[J].山东科技大学学报(自然科学版).2007(12):95-98.
[2]李竹逸,徐琤.数据预处理在基于主成分分析质量管理中的作用[J].商业文化(下半月),2012(2):175.
[3]王亚雄,李建英.主成分分析法在多元质量控制中的应用[J].工业工程与管理,2005,10(3):121-125.
[4]何晓群.现在统计分析方法与应用[M].北京:中国人民大学出版社,1998.
[5]唐懿芳,钟达夫.主成分分析方法对数据进行预处理[J].广西师范大学学报(哲学社会科学版),2002(S1):223-225.
[6]孙彩虹.我国城镇居民消费结构变动的因子分析[J].重庆工商大学学报(西部论坛),2007(1):103-105.
Research on theApplication of Urban Residents'Consumptive Expenditure Based on Equalization of Principal ComponentAnalysis
CHEN Jiang-li
(IT Department,Dianxi Science and Technology Normal University,Lincang,Yunnan 677000,China)
Equalization of principal component analysis based on the traditional principal component analysis method is an improved method using equalization of data preprocessing.In this paper,the per capita consumptive expenditure of urban residents in different regions of China is analyzed by equalization of principal component analysis method,and use Matlab to simulate.Finally the main components of consumptive expenditure are extracted and provide necessary decision support for future research.
equalization;principal component analysis;urban residents;the per capita consumptive expenditure; index system
F126.1
A
1673-1891(2016)01-0074-03
10.16104/j.issn.1673-1891.2016.01.020
2015-12-05
云南省教育厅科学研究基金(2013C037);滇西科技师范学院自然科学、基础应用研究基金项目(LCSZL2013009)。
陈江丽(1984—),女,云南大理人,讲师,硕士,研究方向:数据仓库和数据挖掘。
