基于多元线性回归的PM2.5含量的影响因素研究

张云云，朱家明*，高子云，高彦文

基于多元线性回归的PM2.5含量的影响因素研究

张云云a，朱家明a*，高子云b，高彦文c

(安徽财经大学a.统计与应用数学学院；b.会计学院；c.管理科学与工程学院，安徽蚌埠233030)

针对PM2.5含量的影响因素，利用搜集到的2015年1月1日至7月31日蚌埠地区每日的AQI指数和AQI六项基本监测指标数据，建立了多元线性回归模型，对PM2.5含量与其它5项分指标及其对应污染物含量之间的关系进行定量研究，并通过拟合优度检验、F检验、t检验等方法对模型进行检验，最后得到了准确可靠的多元线性回归模型，此模型具有拟合程度高、简易、直观等优势,为多元线性回归模型在PM2.5含量分析中的应用提供了有力参考。

PM2.5；多元线性回归模型；t检验；MATLAB

0 引言

PM2.5[1]是指环境空气中空气动力学当量直径≤2.5 um的颗粒物，环境保护部于2012年2月29日颁布了新修订的《环境空气质量标准》，新标准首次将PM2.5作为空气质量AQI基本监测指标之一。AQI的其他5项监测指标分别是二氧化硫SO2、二氧化氮NO2、可吸入颗粒物PM10、臭氧O3和一氧化碳CO。有一种研究[2]认为，AQI监测指标中的二氧化硫（SO2）二氧化氮（NO2）一氧化碳（CO）等是在一定环境条件下形成PM2.5前的主要气态物体，因而本文将其他5项基本监测指标作为影响空气中PM2.5含量的因素，利用多元线性回归模型对PM2.5含量与其它5项分指标及其对应污染物含量之间的关系进行定量研究。

1 模型可行性研究

多元线性回归模型是计量经济学中最重要的模型之一，它可以刻画被解释变量与多个解释变量之间的线性关系，并通过最小二乘估计来得到各个回归系数，以此来达到对某些经济变量之间进行定量研究的目的。多元线性回归模型发展到如今，其应用领域已不仅限于经济领域，还包括管理、劳动、教育等多个领域。本文想要利用多元线性回归模型来对PM2.5含量与AQI其它5项分指标及其对应污染物含量之间的关系进行定量研究，首先必须对多元线性回归模型应用到该问题上的可行性进行检验。我们知道被解释变量与各个解释变量的相关关系越强，被解释变量与各个解释变量越有可能存在线性关系，在这里利用收集到的2015年1月1日至7月31日蚌埠地区每日的AQI指数和AQI六项基本监测指标数据，通过MATLAB画出PM2.5与AQI其它5项分指标之间的散点图，如图1-5。

图1 PM2.5-PM10散点图

图2 PM2.5-SO2散点图

图3 PM2.5-CO散点图

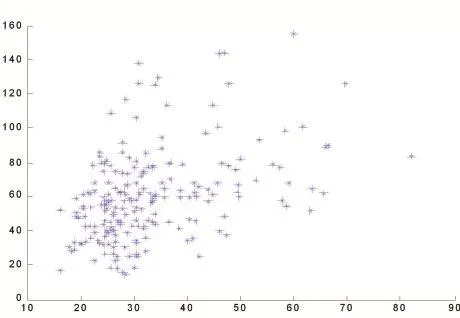
图4 PM2.5-NO2散点图

图5 PM2.5-O3散点图

从图1-5可以看出除PM2.5-O3的散点图较为分散，其余均在一定程度上呈现一定的相关性，因而可以使用多元线性回归模型。在这里用Y来表示被解释变量变量PM2.5，用X1、X2、X3、X4和X5分别来表示解释变量PM10、SO2、CO、NO2和O3，于是各变量的向量形式为：

由此可写出Y与X之间的多元线性回归模型的矩阵形式为：

2 模型变量的选择

建立多元线性回归模型，解释变量的选择尤其重要，计量经济学中一般结合经济学意义选择解释变量，在经济学意义符合的条件下，还要对模型进行变量的显著性检验来确定最终留在模型中的解释变量。在这里首先利用MATLAB对PM2.5与AQI其它5项分指标进行回归分析,得到各回归系数的估计值及其对应的置信区间如表1所示。

表1 回归系数及其置信区间

由表1可以看到只有β5的置信区间包含零，意味着一定的置信区间内，β5的估计值可能为0，若在一定的显著性水平下β5显著为0，则说明X5对Y的影响不显著，所以在这里决定要不要保留变量X5，则需要对变量X5做显著性检验。

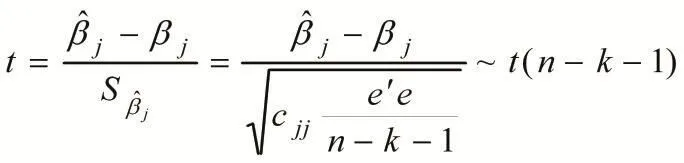
对某变量Xi做显著性t检验，原假设与备择假设分别为：H0∶βj=0，H1∶βj≠0，对构造的t统计量做双侧检验，在原假设成立的条件下，计算t统计量的双边概率p值，再与给定的显著性水平作对比来决定接受或是拒绝原假设。

3 多元线性回归模型的建立

在剔除变量X5之后，再利用MATLAB对Y和剩下的解释变量X1、X2、X3和X4进行回归。得到的回归系数估计值与对应的置信区间如表2所示。

表2 回归系数估计值及其置信区间

由表2可看到回顾系数估计值的在显著性水平为95%的置信区间内不包含零点，由置信水平与显著性水平之间的关系[4]，可知所有的解释变量均可通过显著性检验，从而不用再给变量做显著性检验，所有变量均可保留在模型中，因而可得多元线性回归模型：

Y＝-13.9628＋0.5131X1＋0.5391X2＋24.948X3-0.349X4

上式是用未经标准化的原数据进行回归得到的多元线性回归模型，由于被解释变量与各个解释变量的单位量纲均不一样，因而得到的回归系数不能用以比较各个解释变量对被解释变量的影响大小。为了比较各个解释变量的影响大小，对数据进行标准化处理后再进行回归，得出标准化后的多元线性回归模型：

Y＝0.709X1＋0.167X2＋0.365X3－0.154X4

由标准化后的多元线性回归模型中的各个回归系数可以看出，PM10、SO2、CO含量与PM2.5含量之间存在正相关关系，NO2含量与PM2.5含量之间存在负相关关系，且由标准化后回归系数可知各个解释变量对被解释变量的影响大小排序为PM10> CO>SO2>NO2，且调整后的回归系数具体数值量化了各个解释变量对被解释变量的影响大小，从而达到了定量研究的目的。

4 模型的检验

4.1 拟合优度检验

多元线性回归方程的的拟合优度检验[3]采用R2检验统计量，称为可决系数，其数学定义为：

R2反映了回归方程所能解释的部分（回归平方和）占总离差平方和的比例。由上式可知，R2取值在0～1之间，越接近于1，说明回归方程对样本数据点的拟合优度越高；反之，越接近于0，说明回归方程对样本数据点拟合优度越低。利用上面公式可计算得到模型的R2等于0.844 1，可知拟合优度较好。

4.2 回归方程的显著性检验

多元线性回归方程显著性检验[3]的原假设为各个偏回归系数与零同时无差异，它意味着当偏相关系数同时为零时，无论各个xi取值如何变化都不会引起Y的线性变化，所有X无法解释Y的线性变化，Y与X全体不存在线性关系。在原假设成立的条件下，统计量

服从自由度为（p,n-p-1）的F分布。如果概率p值小于给定的显著性水平a，则应拒绝原假设，认为偏相关系数不同时为零，被解释变量y与解释变量x全体的线性关系显著，可以用线性模型反映它们之间的关系；反之，如果概率p值大于给定的显著性水平，则不应拒绝原假设，认为偏相关系数同时为零，被解释的变量Y与解释变量的全体的线性关系不显著，用线性模型描述和反映它们之间的关系是不恰当的。

利用上述F值计算公式，通过MATLAB计算可得出F值为280.239 2，对应计算出的p值为0，在显著性水平为0.01的情况下拒接原假设。因而可知模型通过了回归方程的显著性检验，即被解释变量Y与解释变量全体的线性关系显著，可以用线性模型反映它们之间的关系。

4.3 异方差性的检验

建立多元线性回归模型的基本假设之一是随机误差项具有零均值同方差性，若对于不同的样本点，随机误差项不再是常数，而是互不相同，则认为出现了异方差性。随机误差项存在异方差会引起参数估计量、变量的显著性检验失去意义等后果，因而我们有必要在这里对随机误差项是否存在异方差性进行检验，随机误差项用来近似估计，其中：

图6 随机误差项近似估计量序列

可以证明，在同方差性的假设下，从该辅助回归得到的可决系数R2与样本容量的乘积渐近地服从自由度为辅助回归方程中解释变量个数的x2分布[3]，在这里即为：

4.4 异常值处理

利用MATLAB对残差及其置信区间进行分析，其异常值情况如图7所示。

由图7可知在置信水平为95%的情况下残差置信区间不包含残差真值的样本量为11，其占样本总量的5%左右，符合置信水平的概率解释，也即置信水平为95%是指能保证95%的由样本计算出的置信区间，包含估计量真值。图7中红线就是指由样本计算出的置信区间不包含残差真值的区间，对异常值进行剔值处理，发现异常值始终保持在10个左右，且每一次剔值都会减少样本量，从而剔值处理反而增大了异常值的比例，因而在这里不对异常值进行剔值处理，异常值比例较低，不会对模型产生太大的影响。

图7 置信水平为95%的残差的置信区间

5 结语

本文利用2015年1月1日至7月31日212 d的AQI指数和AQI六项基本监测指标数据建立了多元线性回归模型，对PM2.5含量与其它5项分指标及其对应污染物含量之间的关系进行了定量研究。研究结果表明AQI其他5项分指标除O3外其余的指标确实都是影响PM2.5含量的因素，且影响作用最大的是指标PM2.5，其次是CO,再其次为SO2，影响作用最小的为NO2，且通过调整后的回归系数，具体量化了各个指标对PM2.5含量的影响。

另外，经过适当修改，完全可以应用到其他空气污染物、河流污染物和土壤污染物含量的影响因素的相关问题中，可以为多元线性回归模型在环境领域的应用提供了一定的参考。

[1]黄辉军，刘红年，蒋维楣，等.南京市PM2·5物理化学特性及来源解析[J].气候与环境研究，2006,11（6）：715-716

[2]刘洁，张小玲，徐晓峰，等.北京地区SO2、NOx、O3和PM2·5变化特征的城郊对比分析[J].环境科学，2008,29（4）:1060-1061

[3]李子奈，潘文卿.计量经济学[M].北京：高等教育出版社，2010:73-77.

[4]茆诗松，程依明.概率论与数理统计教程[M].北京：高等教育出版社，2011:236-240.

[5]覃太贵,尹辉.PM2.5相关因素及分布演变的研究[J].数学的实践与认知，2014,44（15）：7-10.

Research on the FactorsAffecting the Content of PM2.5 Based on Multiple Linear Regression Model

ZHANG Yun-yuna,ZHU Jia-minga,Gao Zi-yunb,Gao Yan-wenc
(a.School of Statistics and Apply Math;b.Accounting Institute;c.Management Science and Engineering,Anhui University of Finance and Economics，Bengbu,Auhui 233030，China)

Aiming at the problem about factors affecting the content of PM2.5,Using collected data about January 1, 2015 to July 31,2015 daily AQI index and the six basic monitoring indicators in Bengbu，conducting quantitative research about the relationship between PM2.5 content and other five sub-indicators and their corresponding levels of contaminants by applying multiple iinear regression model,and through the goodness of fit test,F test,t test method to test the model,and finally get accurate and reliable multiple linear regression model,this model has a high degree of fit,simple and intuitive,and other advantages,providing a strong reference for the multiple linear regression model in PM2.5 content analysis.

PM2.5;multiple linear regression model;t test;MATLAB

X511

A

1673-1891（2016）01-0017-04

10.16104/j.issn.1673-1891.2016.01.005

2015-05-27

国家自科基金项目（11301001）；安徽财经大学教研项目（acjyyb2014104）。

张云云(1993—)，女，安徽六安人，研究方向：应用数学与数学建模。*为通信作者。