养老金与资本市场关系及对中国养老金发展的启示
——基于34个国家的向量误差修正模型的实证分析
2016-08-02杨一帆程子建
杨一帆 程子建
(1.西南交通大学国际老龄科学研究院;2.西南交通大学公共管理与政法学院 四川成都 610031)
·经济与管理·
养老金与资本市场关系及对中国养老金发展的启示
——基于34个国家的向量误差修正模型的实证分析
杨一帆1程子建2
(1.西南交通大学国际老龄科学研究院;2.西南交通大学公共管理与政法学院四川成都610031)
摘要:本文利用OECD国家养老金与资本市场数据进行二者的因果分析,并采用条件异方差方法得出四种程度不同的互动关系集,然后建立起协整和向量误差修正模型分析养老金投资与资本市场的相互作用,对残差项进行拉格朗日乘子检验验证残差不存在自相关,佐证了模型定阶的稳健性。拟合结果显示,养老金与资本市场的规模扩张和稳定性的关系因各国资本积累水平、风险偏好和管理体制方面的差异而有所不同,最后得出中国养老金在入市时机、投资主体精简与统一、投资风险控制、养老金投资配套改革方面的启示。
关键词:养老金投资;格兰杰因果分析;向量误差修正模型
随着经济迅猛发展以及社会风险损失预期值的扩大,养老保险作为老年人晚年生活保障在实际生活中发挥越来越重要的作用。由于前期各国采取的待遇确定型(Defined Benefit,DB)养老金存在诸如入不敷出、供给需求不匹配、难以可持续发展等问题,因此1980年以后多数国家将养老金转向缴费确定型(Defined Contribution,DC),它要求企业为每个职工建立个人账户,个人账户采用完全积累制,职工退休后的收益取决于资本市场波动、资产配置组合收益、投资行为决策等因素。由于DC型养老金收益自负盈亏的特点,一方面可以解决国家财政压力,另一方面又可以扭转过去养老金收益增长率常年低于通货膨胀率的尴尬局面。因此对DC型养老金的研究受到学者广泛关注。
一、已有研究回顾
近年来,对养老金与资本市场进行研究的文献日渐增多。英国学者圣格(Singh)从理论和实证分析层面上对发展中国家养老金投资与资本市场之间互为因果关系提出质疑[1]。Vittas(2003)运用实证模型证明,在拉美国家中养老金投资与资本市场间确实存在显著且良性的互动关系。学者张松[2](2006)以经济合作与发展组织(OECD)中34 个国家1980—2001年近21年间的宏观经济指标与养老金数据为研究对象,运用Granger因果关系检验法得出“单向因果”、“双向因果”以及“没有因果”三类关系集,其中以养老金单向促进资本市场发展为多数,并且创新性提出一般性约束条件,但并未就约束性条件的传导机制进行量化。而从投资行为角度进行研究的文献中,席红辉(2008)对比了美国与中国养老金的特征,分析了其对养老金积累绩效的影响。Brennan、Schwartz 、Lagnado(1997)分析了基于债券、股票和现金三种资产的动态投资问题,他们假设短期利率、长期债券利率和股票的分红收益均服从马尔可夫过程,并证明考虑资产预期收益的策略将显著提高收益率。Brennan(1998)研究了长期投资者的投资组合问题,研究表明不确定预期收益下,投资者风险资产配置比例变化的方向取决于对风险的容忍程度。Xia(2004)基于连续时间模型证明了忽略预期将大大提高投资者的机会成本。Battocchio、Menoncin研究了在通货膨胀下DC 型养老金资产的最优配置问题。理论研究与经验表明养老金与资本市场的互动不是必然的[3]。本文研究即是在前人基础上,将养老金与资本市场的交互作用进行格兰杰因果分析,并通过最新收集数据对这种关系运用模型进行探究,得出结论并提出建议。
养老金投资与资本市场的互为因果的运动过程可以大体分为两大类,一是养老金投资与资本市场规模扩张的互动关系,二是养老金投资与市场稳定性的互动关系[4]。稳定性、长期性、规模性的资金流对资本市场的发展至关重要,而养老金投资作为一种逐利投资已经成为资本市场发展的稳定利器[5]。作为一种长期负债,养老金证券化之后必然要在不同的时期寻求期限、风险、收益相匹配的长期资产,从长期来看,其稳定性要远优于普通投资者。这种结果能很大程度上改变市场交易过于频繁。其追求长期稳定收益的意愿,能避免其作出像普通投资机构追求绝对收益一样的非理性投机行为,降低市场波动。
二、研究方法
在构建模型之前,为了排除变量间可能存在伪回归,先期就需要进行单位根检验(Unit Root Test)。常用的单位根检验有Dickey-Fuller检验、Augment Dickey-Fuller检验、Phillips-Perron单位根检验、DF-GLS检验。对于序列{yt} ,考虑模型:
yt=a1+a1yt-1+εt
其中,{εt}为白噪声。若-1
对DF检验另一种修正是PP检验。PP检验采用一阶自回归和异方差自相关稳健的标准差,即:
Δyt=b0+δyt-1+εt
格兰杰因果(Grange Casuality)应用于模型中目的是确定一个变量是否为另一个变量的格兰杰因,其基本思想为:如果x是y的格兰杰因,那么给定y的过去值之后,x的过去值还可以帮助预测y的未来值。在条件异方差的算法前提下Granger Casuality的模型为:
yt=γ+Σi=1pαiyt-i+Σj=1qβjXt-j+εt(检验原假设H0:β1=β2=……=βq=0)当且仅当尚不能拒绝H0时,则称x是y的“格兰杰因”,反之亦然。
向量误差修正模型(Vector Error Correction Model)相关变量间可能存在长期的均衡关系,变量的短期变动就是向着这个长期均衡关系的部分调整,考虑AR(1),yt=a0+a1yt-1+εt。
假设a1<1,则{yt}为平稳过程。对方程两边求期望值,并令长期均衡y=E(yt)=E(yt-1),则可得y=a0/(1-a1)。将a0=(1-a1)y代回AR(1)的原方程,并在方程两边同时减去yt-1,整理后得到:Δyt=(1-a1)(y-yt-1)+εt
以上是AR(1)的误差修正模型,它将Δyt表达为对其长期均衡的偏离(y-yt-1)的部分调整加上扰动项。对于协整的秩为h的VEC模型,
yt=v+δt+Φ1yt-1+……+Φpyt-p+εt
可以导出向量误差修正形式(VECM)
Δyt=v+δt+αβ’yt-1+Τ1Δyt-1+Τ2Δyt-2+……+ΤpΔyt-p+εt
其中,Γs=-(Φs+1+……Φp),αβ’=-(In-Φ1-Φ2-……-Φp)。
αβ为两个nxh的满列秩矩阵(αβ不唯一),这样zt-1=a’yt-1即为误差修正项,代表了变量间的长期关系,α是调整参数矩阵。
三、格兰杰因果检验结果
首先对OECD中34个样本国家的养老金投资与资本市场指标进行格兰杰因果分析。结果见表1。
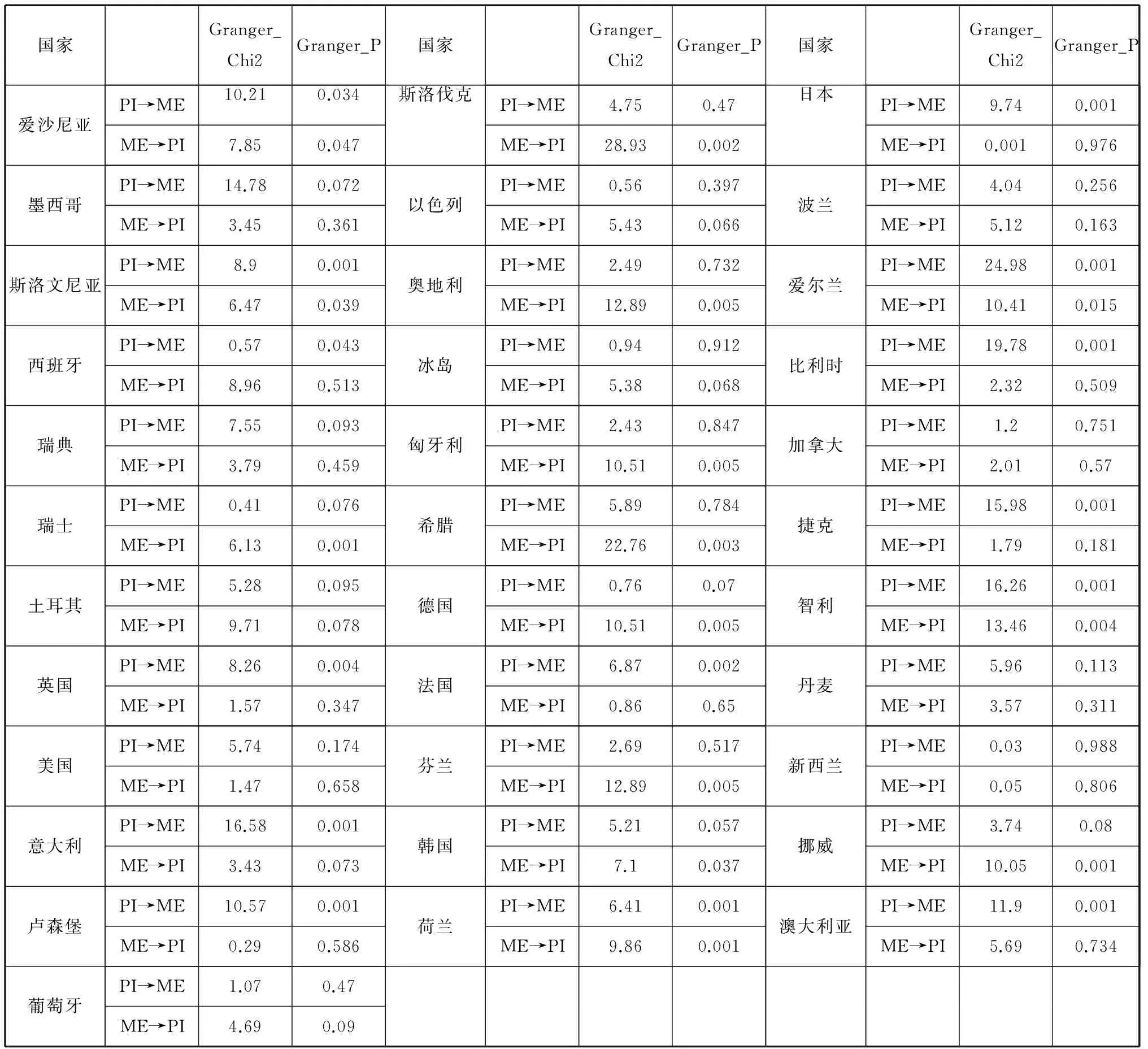
表1 养老金投资与资本市场格兰杰因果关系分析
其中,PI表示养老金投资,ME表示资本市场。当给定显著性水平为5%时,PI→ME表示养老金单向促进资本市场发展,ME→PI表示资本市场发展单向促进养老金投资,PI↔ME表示养老金投资与资本市场发展互为因果关系,PI!=ME表示养老金与资本市场发展不存在互为因果关系。以此为划分依据,将OECD中34个国家划分为四类,如表2所示。

表2 部分OECD国家养老金投资与资本市场因果关系表
四、实证分析
前期格兰杰因果分析得到,在以上四类国家中均是发达国家与发展中国家并存,理论上由于发达国家资本流动性和经济开放程度要强于发展中国家,开放下的资本市场作为一个整体,不同国家可视为独立的机构投资者参与其中,而不同国家因其不同的积累水平和风险偏好,它们在养老金资产配置上面的策略[6]也是不尽相同的,因此有必要进一步探究造成这种差异性的原因。养老金投资与资本市场的关系如图1所示。
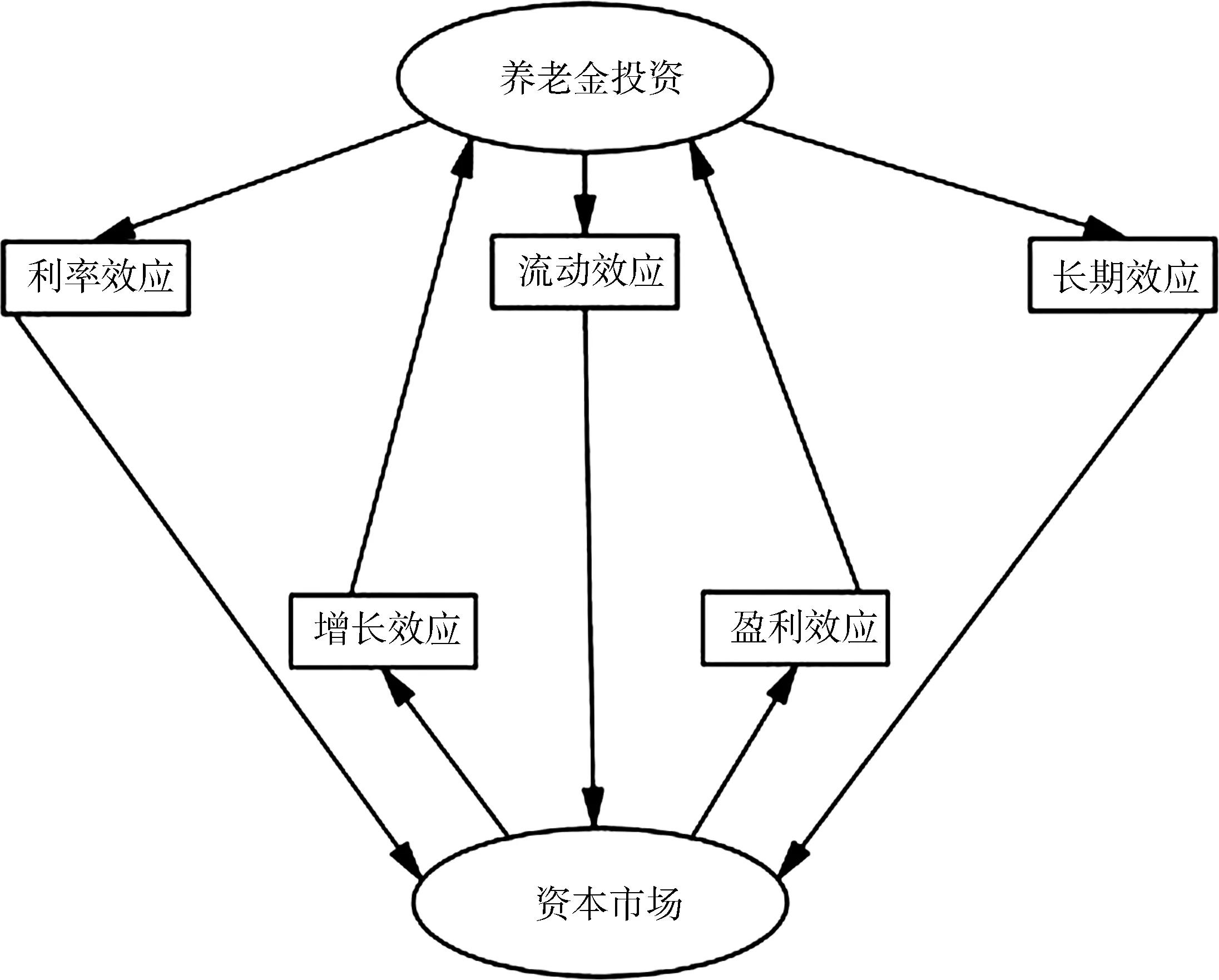
图1 养老金投资与资本市场关系
张松(2006)认为养老金投资作用于资本市场有三大效应传导机制。其一是利率效应:养老金投资支出增加导致市场利率下降,进而抬高养老金融衍生物价格,最终推动资本市场发展。其二流动效应:养老金投资支出增加致使个人资产组合流动性下降,会导致流动性资产需求上升,最终推动资本市场发展。其三长期效应:养老金投资支出增加使长期储蓄比例提高,优化了社会储蓄结构,从而增加了长期资金供给,进而促进资本市场发展。
另一方面,资本市场反作用于养老金投资的两大效应传导机制。其一增长效应体现在,市场发展通过乘数-加速数效应促进实体经济和社会总收入的增加,养老金投资的供给来源得到增多;其二盈利效应表现在,资本市场的发展为养老金投资支出提供复杂多样的投资产品和杠杆工具,良好的市场环境总能使养老金投资收益得到预期回报。[2]
基于五大效应基础上,选取变量如下:
(1)利差(interest_margin),即贷款利率减去存款利率;
(2)股票交易周转率(stockexc_rate),周转率即指一定时期内股票交易总额除以该时期上市公司平均市值的结果;
(3)上市公司资本总额占gdp百分比(capital_gdp);
(4)S&P全球股票指数(sp_index), 用来衡量股市中的美元价格变化,其中包括S&P/IFCI和S&P/Frontier BMI国家指数;
(5)养老金支出占gdp百分比(peninv_gdp);
(6)gdp增长率(gdp_inc);
(7)贷款的风险溢价(loan_risk);
(8)股票交易额占gdp百分比增长率(stockgdp_inc)。
养老金投资与资本市场规模扩张关系模型:
(1)ΔD_peninv_gdpt=β1(D_peninv_gdpt-1+β2D_capital_gdpt-1+μ0)+ μ1
ΔD_capital_gdpt=α1(D_peninv_gdpt-1+α2D_capital_gdpt-1+ψ0)+ψ1
养老金投资与资本市场稳定关系模型:
(2) ΔD_peninv_gdpt=Φ1(D_peninv_gdpt-1+Φ2sp_indext-1+ξ0)+ξ1
Δsp_indext=γ1(D_peninv_gdpt-1+γ2sp_indext-1+ω0)+ω1
其中D_capital_gdp衡量资本市场规模扩张速度;D_peninv_gdp衡量养老金投资增长率;sp_index代表各国股票价格指数的波动,其绝对值的大小反映资本市场稳定程度。时间序列往往带有非平稳趋势,因此需要对变量进行平稳性检验[7],采用Dickey-Fuller test对各变量实施单位根假设检验,结果表明上述变量中除少数不平稳,其余均通过单位根假设检验。随后不平稳变量对其一阶差分再进行检验后取得平稳。
考虑到市场经济的信息滞后性,需要对模型进行定阶,综合采用贝叶斯信息准则(BIC)和赤池信息准则(AIC)等。如表3所示。
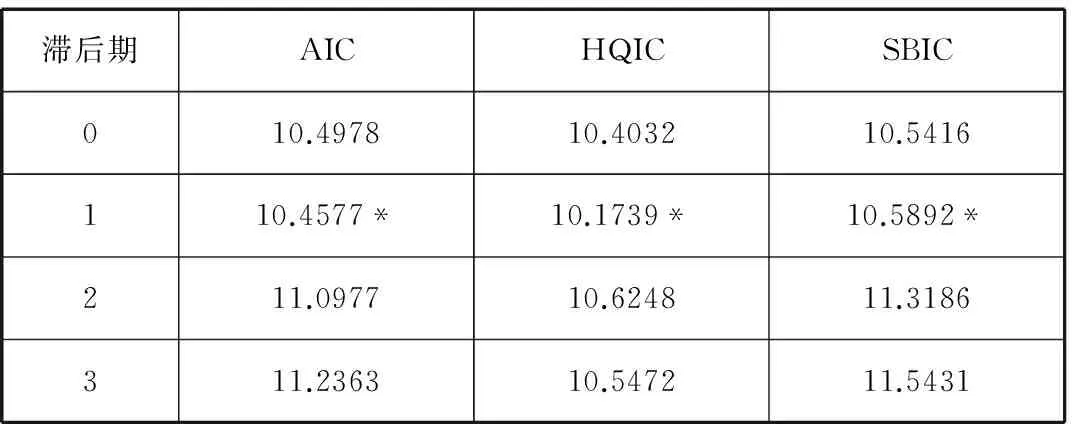
表3 滞后阶数的确定
注:*表示在5%水平上显著
根据信息准则最小的原则,在90%的置信度下,选取变量滞后1期值为最佳。在下文进行的VEC模型的统计回归中,将进一步检验滞后阶数的可靠性,然后进行约翰逊协整检验。对于VEC模型:
Δyt=v+δt+αβ’yt-1+Γ1Δyt-1+Γ2Δyt-2+……+Γp-1Δyt-p+1+εt
这是对差分序列Δyt的建模,模型中的常数向量v未差分序列有线性趋势,δt意味着未差分序列有二次趋势,将v和δ写成如下形式:
v=αμ+γ;δ=αpt+ν;δ=αρt+τt
其中,μ和ρ都是hx1的参数向量,γ和τ为nx1的参数向量;且γ和αμ正交,τ和αρ正交,因此得到VEC模型:
Δyt=α(β’yt-1+μ+ρt)+Γ1Δyt-1+Γ2Δyt-2+……+Γp-1Δyt-p+1+γ+τt+εt
由此得到协整关系检验结果如表4所示。

表4 协整关系检验结果
根据结果,在rank=0时,迹统计量的值为33.6551,大于5%临界值15.41,在rank=1时,迹统计量的值为10.0023,小于5%临界值10.7625,因而不能拒绝存在1个或小于1个协整关系的原假设。综合可以得到协整关系为1个。
模型采用ML算法拟合VEC模型。拟合度如表5所示,可以证明模型的拟合度优,估计值的稳健性可靠。

表5 模型拟合优度
拟合模型的结果如表6所示。
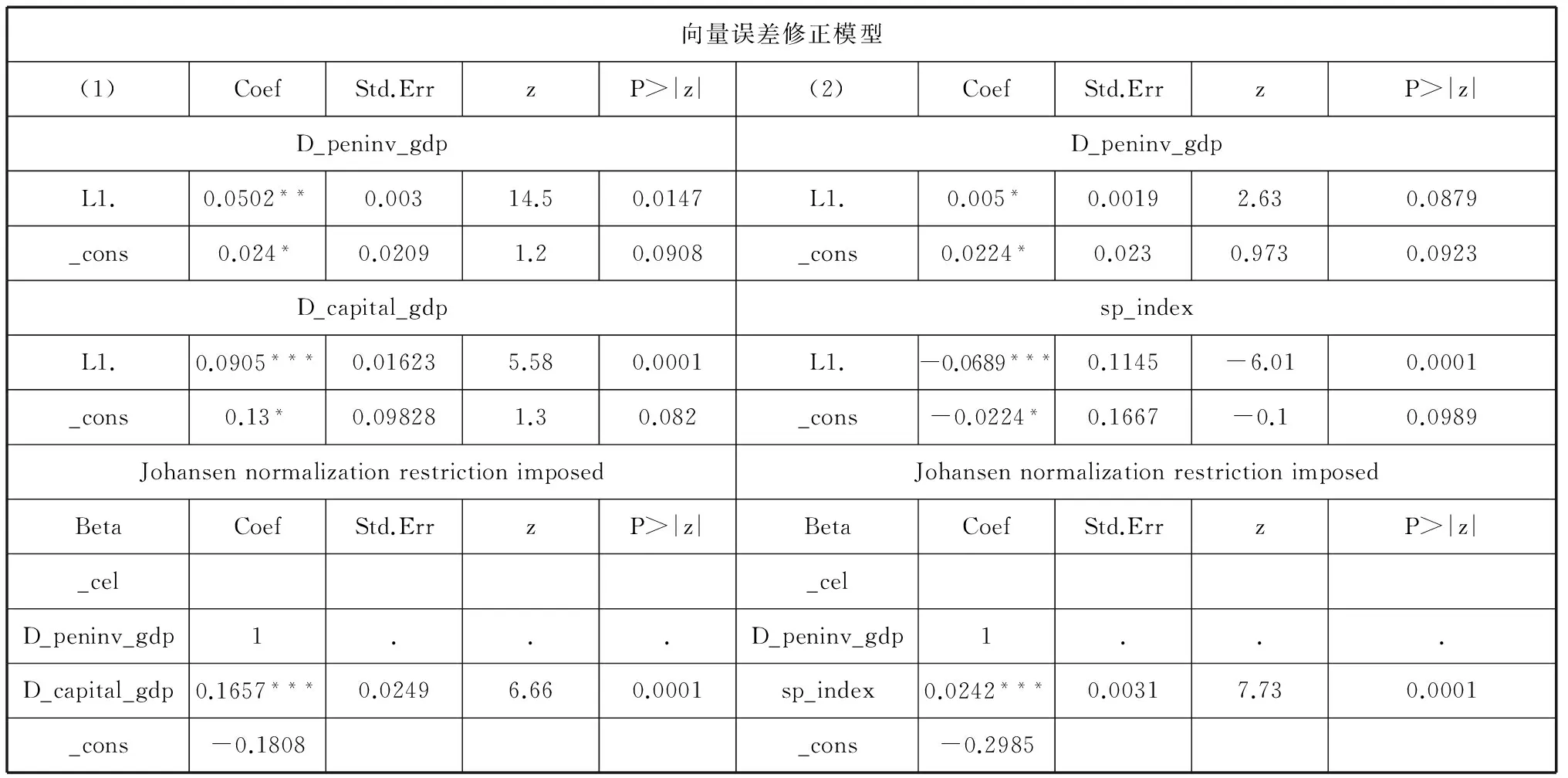
表6 养老金投资对资本市场的规模扩张和稳定性的影响
注:***、**、*分别代表1%、5%、10%显著性水平
由上述系数矩阵可以得到方程组:
(1)ΔD_peninv_gdpt=0.05 (D_peninv_gdpt-1+0.16D_capital_gdpt-1-0.18)+ 0.024
ΔD_capital_gdpt=0.09(D_peninv_gdpt-1+0.16D_capital_gdpt-1-0.18)+0.13
(2)ΔD_peninv_gdpt=0.005(D_peninv_gdpt-1+0.02sp_indext-1-0.29)+0.022
Δsp_indext=-0.06(D_peninv_gdpt-1+0.02sp_indext-1-0.29)-0.023
对残差进行的拉格朗日乘子检验可以看到在5%的显著性水平下,尚不能拒绝滞后1期没有自相关的原假设,也就是说残差不存在自相关,同时对残差进行的正态性检验可以看到,不能拒绝残差分别服从正态分布的原假设,也不能拒绝两方程的残差服从联合正态分布的假设。如表7所示。
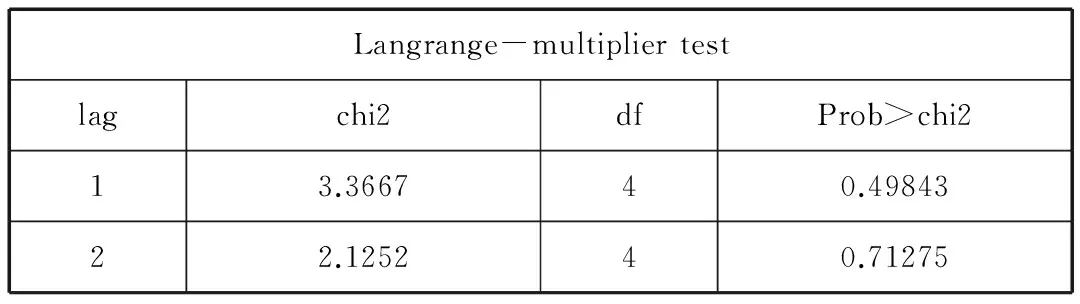
表7 残差自相关性检验结果
通过向量误差修正模型可以得出,在方程组(1)中当D_peninv_gdpt为被解释变量时,D_peninv_gdpt-1和D_capital_gdpt-1显著为正,系数分别为0.05和0.008,说明上一期的养老金投资增长与资本累积确实对当期养老金投资收益产生缓慢的正向作用。当D_capital_gdpt为被解释变量时,D_peninv_gdpt-1对其作用系数为0.09,同样是缓慢而稳定的,合理的解释是因为养老金投资数额庞大,与资本市场进行相互作用时需要一个稳定的运动过程,这样有助于改善经济时滞性问题,给予市场参与者足够的决策时间[8],与前期理论分析相一致。在方程组(2)中,当sp_indext为解释变量时,D_peninv_gdpt-1和sp_indext-1系数显著为负,分别为-0.06和-0.0012。数理上表示为若D_peninv_gdpt-1(上一期养老金投资支出)sp_indext-1(资本市场上一期价格波动)增加一个单位时,对sp_indext(当期价格波动)分别产生6%和0.12%消极作用,同时调整系数的绝对值相对较小,这保证了若当期资本市场价格长期偏离均衡值时,二者交互作用会使其朝着长期均衡值下调,这与前期理论分析——养老金投资增长对稳定资本市场价格变动具有消极作用,而上一期资本市场的价格波动会对当期波动产生负向影响——相吻合。因为养老金作为机构投资者,其本身长期性和固定性的特点可以在一定程度上缓和众多参与者间的矛盾,参与资本市场运作可以避免交易的频繁进行从而稳定市场价格波动。而上一期资本市场价格变动会对当期价格产生负向影响,合理的解释是,在市场经济体制下,非理性市场参与者会受到价格时滞的影响而作出逆市场风向的行为。
五、启示
本文结合OECD34个国家1980年至2014年间养老金与资本市场数据来研究二者之间的关系,发现两者互动关系在不同国家的表现不同,这说明养老金与资本市场的互动关系并不是必然发生的。形成良好的传导路径需要媒介的支持,同时这也受到资本市场现状、养老金法律法规和管理体制等诸多约束性条件限制。而我国资本市场相对西方国家起步较晚,资本流动相对僵化、配套设施不完善、养老金法律法规不健全、管理体制混乱等一系列问题都对养老金可持续发展构成严重威胁。因此从本研究得出的养老金在中国发展的启示可以从入市时机、投资主体精简与统一、投资风险控制、养老金投资配套改革[8]四个方面来阐述。
首先,实证分析可以得到,高度发达与自由的资本市场并不是进行养老金投资的充分条件,也就是说确保养老金保值增值,资本市场并不是唯一的限制性条件,而养老金在资本市场不成熟的国家如智利、爱沙尼亚、斯洛文尼亚等国,二者互动作用却更明显。因此我国养老金决不能等资本市场发展成熟了再入市,必须对现行养老金管理体制进行深度改革,不能眼看养老金贬值而入不敷出,要通过市场的力量缓解财政负担,养老金改革相关配套法律法规也应以促进其可持续发展为方向进行修订。
其次,养老金投资主体应是一个统一的、行为和决策高度一致的机构投资者,而现行的养老金筹集与发放权力分散在两千多个独立的行政单位手中,通过前期理论分析可以知道,养老金投资需要一个稳定而长期的营运过程,过多的参与者会打破这一长期均衡体制,造成资本市场的动荡,不利于养老金的长期受益。而进行全国统筹在目前来看成本高、难度大。因此需要将养老金的筹集与发放权统一到省一级的主体中,并采取信托方式进行营运。
再次,养老金投资作为一种证券化的投资工具,其投资模式和规则也应遵从金融衍生品的投资方式,因养老金债务长期性、风险性、收益性的特点,需要在市场上寻找期限匹配、风险匹配、收益匹配的相关投资产品,做到资产负债匹配原则才能在源头避免管理混乱。同时相关部门应放宽投资管制,提高投资者数量和质量。
最后,养老金的筹集与发放虽然掌握在政府手里,但是其投资活动的开展需要暴露在公众的监督之下,应建立完善的《养老金投资运营管理办法》,明确投资范围及资产负债匹配原则,建立投资机构评估准则,丰富第三方评估机构,建立信息披露机制,财务报表和税务报表应由有资质的会计师事务所进行审计,确保一系列投资行为在法律框架下进行。
参考文献:
[1]Singh,Ajit.Pension Reform,the Stock Market,Capital Formation and Economic Growth:A Critical Commentary on the World Bank’s Proposals[J].InternationalSocialSecurityReview,Vol.49,1996:21-43.
[2]张松.养老基金与资本市场互动的理论与实证研究——兼论中国养老金资本市场良性互动的政策思路[M].成都:西南财经大学出版社,2006:5-17.
[3]魏加宁.养老保险与金融市场: 中国养老保险发展战略研究[M].北京:中国金融出版社,2001:7-21.
[4]齐明珠.养老金计划改革的宏观经济影响: 中国与发达国家的比较研究[J].市场与人口分析,2001(11).
[5]林义.养老基金与资本市场互动发展的制度分析[J].财经科学,2005(4).
[6]朱铭来.养老金投资对资本市场的影响研究——基于 OECD 国家面板数据的实证分析[J].中国物价,2015(3).
[7]张佩.中国养老金融创新发展:现实障碍、经验借鉴与应对策略[J].西南金融,2014(7).
[8]唐运舒.养老金投资与资本市场互动发展研究综述——兼论对中国基本养老金市场化投资启示[J].华东经济管理,2012(8).
[责任编辑刘瑜]
收稿日期:2016-03-24
作者简介:杨一帆(1984—),男,副教授,西南财经大学与德国马普学会国际社会保障研究所联合培养博士,西南交通大学国际老龄问题研究院副院长,研究方向:社会保障、养老经济。
中图分类号:F842.6;F832.5
文献标志码:A
文章编号:1672-8505(2016)04-0068-07
The Relation Between Pension and Capital Market and Its Enlightenment for China Pension Development:An Empirical Analysis Based on Vector Error Correction Model of 34 Countries
YANG Yi-fan1CHENG Zi-jian2
(1.ResearchInstituteofInternationalAgingScience,SouthwestJiaotongUniversity;2.SchoolofPublicManagement&PoliticsandLaw,SouthwestJiaotongUniversity,Chengdu,Sichuan, 610031,China)
Abstract:This paper performs the cause-and-effect analysis via the data of OECD national pension funds and capital market and finds 4 interaction relation sets of different levels by using the method of conditional heteroscedasticity. And it then establishes the cointegration and vector error correction model to analyze the mutual effect between pension investments and capital markets. The examination of the residual item via Lagrange multiplier test verifies the fact that the residual item has no self-correlation, which proves the stability of the model order. The results show that the relation between pension investment and capital market expansion and stability varies according to different capital accumulation, risk preferences, and management system. Finally, the essay, based on the international comparative analysis, clarifies the enlightenment of China pension development in several aspects.
Key words:pension investment; Grange causality; Vector Error Correction Model
