城际铁路常用跨度简支箱梁频率限值研究

简方梁　徐升桥　田　杨

(中铁工程设计咨询集团有限公司，北京　100055)



城际铁路常用跨度简支箱梁频率限值研究

简方梁徐升桥田杨

(中铁工程设计咨询集团有限公司，北京100055)

摘要根据目前城际铁路桥梁设计相关资料，拟定城际铁路常用跨度简支箱梁的截面尺寸，建立有限元模型，进行结构的竖向基频计算，根据设计荷载效应大于等于实际运营车辆荷载效应的原则，得出各跨度简支梁实际运营车辆最大容许动力系数。应用车辆-桥梁耦合振动分析理论，进行动力仿真分析，得到各跨度简支梁在实际运营车辆下的实际动力系数。通过比较得出，按照国际铁路联盟规定的桥梁结构频率下限值设计，能够满足结构安全及舒适性要求。

关键词城际铁路简支梁频率动力系数

1概述

城际铁路桥梁结构基频作为控制结构体系刚度及列车动力效应最基本的参数，一方面决定了结构的安全性及旅客列车的运营舒适性，另一方面影响结构的梁高，对工程结构的造价有重要影响，研究其合理的限值有重要意义。

目前，国际上关于铁路桥梁设计荷载及基频限值方面的研究主要分为两类，第一类以国际铁路联盟及欧美各国为代表，另一类以日本为代表。

国际铁路联盟采用的铁路设计荷载为概化荷载，与之相关的动力系数也为概化动力系数，二者的乘积代表了铁路桥梁活载设计值。为使设计结果大于实际荷载效应，保证结构的设计安全，在实际运营荷载一定的情况下，需控制实际结构的动力系数，采用的方式为控制结构的基频，国际铁路联盟对常用跨度简支梁的基频限值分为上限和下限，均为跨度L的函数。其对数坐标如图1所示[1]。

其中，下限值为分段函数形式，表达为

(1)

其中，f0为结构基频/Hz；L为桥梁跨度/m。

图1　UIC规范规定的简支梁自振频率限值

在满足结构基频限值的前提下，结构的动力系数只与结构的加载长度有关，对一定跨度简支梁为一定值。针对不同的列车运行活载，通过将标准活载乘以一个大于1或小于1的系数来体现设计荷载的区别。

国际铁路联盟的动力放大系数中不包含速度相关效应，仅与跨度有关，这与实际结构的动力响应不符合，但是简便易用，通过对频率的控制，可以很轻易的初拟桥梁结构的断面形式，对于设计者有较好的参考价值。

日本铁路桥梁设计思路为：采用与实际运营模式很接近的荷载模式，而对结构的冲击系数给予细致的规定。其冲击系数分为两个方面：速度效应的冲击系数，车辆振动的冲击系数。最终结构的冲击系数为二者的乘积形式[2]，表达为

(2)

其中，ia为速度相关的冲击系数，ic为车辆振动冲击系数。ic表达为

(3)

其中，Lb为桥梁的跨度。

速度效应的冲击系数与速度参数有关，速度参数表达为

(4)

式中：V为列车运行的最高速度；n为构件的基本固有频率。

速度效应的冲击系数与速度参数之间的关系以图表的形式给出，典型图表如图2所示。

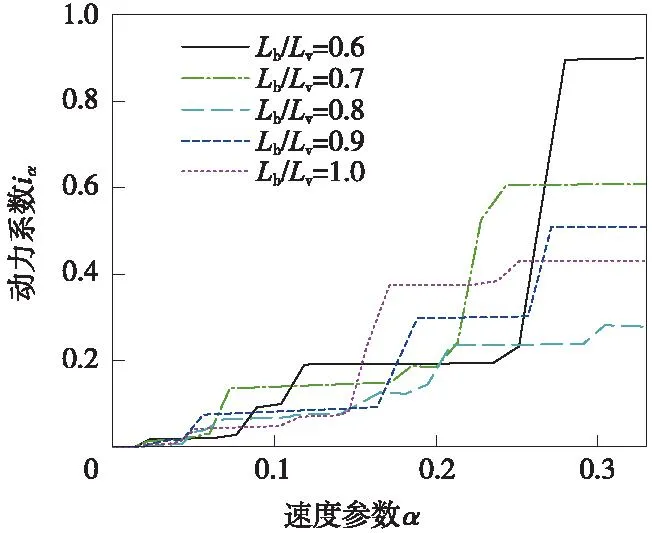
图2　冲击系数与速度参数之间的关系

图2中给出的是速度参数小于0.33的关系图，可见在此情况下，冲击系数一般不会太大。

应用车辆-桥梁耦合振分析理论，通过动力仿真分析计算CRH2列车以不同速度通过不同基频桥梁的动力响应，以设计结构响应大于等于实际仿真车辆响应为准则，确定频率的限值标准。

2箱梁基本尺寸及频率计算

本次对城际梁20 m、24 m、32 m三种常用跨度简支箱梁进行研究。梁体结构尺寸及桥面布置参照相关资料拟定[3-6]，20 m双线无砟箱梁拟定4种梁高，分别为1.10 m、1.15 m、1.20 m、1.35 m；24 m双线箱梁梁高取为1.35 m、1.40 m、1.50 m、1.60 m；32 m双线箱梁梁高取为1.90 m、1.95 m、2.00 m、2.20 m。典型的跨中断面如图3所示，跨中等厚段腹板厚度320 mm，顶板厚度320 mm，底板厚度250 mm。

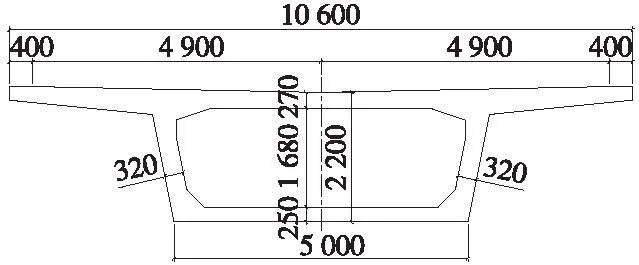
图3　箱梁典型断面(单位：mm)

下部结构采用常规墩高及通常地质条件下的地基刚度。结构自重取为26 kN/m3，全部桥面二期恒载取为140 kN/m。

采用Midas Civil建立有限元模型(如图4所示)。

图4　MIDAS有限元分析模型

进行频率分析，得到各跨度各梁高结构对应的竖向基频(如表1所示)，并仿照UIC频限值公式，给出各梁竖向基频与跨度的关系。从中可见，各跨度选用梁高下结构的频率基本在UIC频率限值附近，频率随梁高的降低而降低。

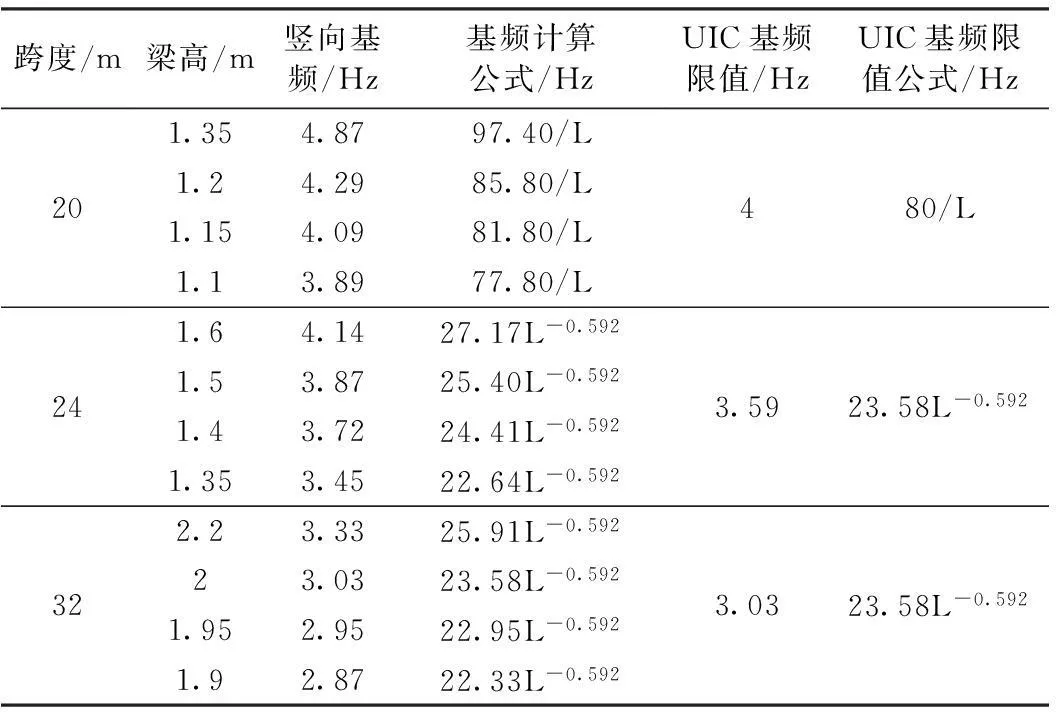
表1　各跨度梁高结构基频及UIC限值

3各跨度箱梁容许动力系数

根据设计车辆荷载效应大于等于实际车辆荷载效应的原则，城际梁采用ZC设计荷载，动力系数按照相关设计规范选取[7]，实际运营荷载采用CRH2型车辆荷载，通过有限元静力计算，得到CRH2型荷载各跨度的最大容许动力系数(如表2所示)。从中可见：对于CRH2型车，20 m跨度简支梁实际最大容许动力系数为2.391，24 m跨度简支梁最大容许动力系数为2.428，32 m跨度简支梁最大容许动力系数为2.604。

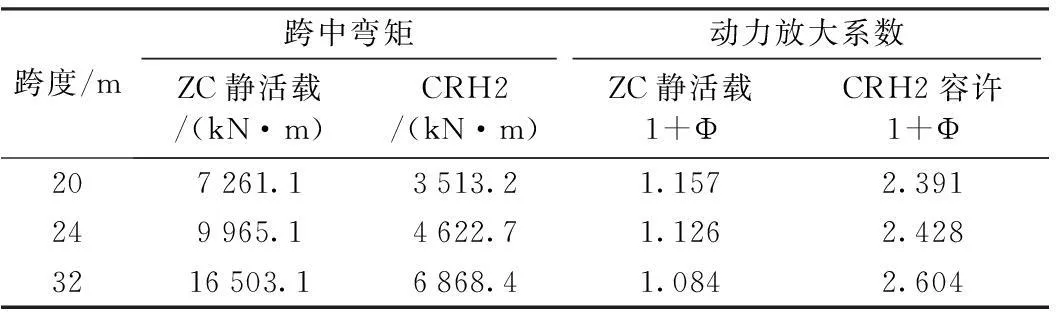
表2　CRH2型车容许动力系数

4常用跨度城际梁动力仿真分析

采用车辆-桥梁耦合动力仿真分析模型对各常用跨度典型高度城际梁进行动力仿真研究，车桥-桥梁耦合动力分析的相关理论可参考相关文献[8-12]。

4.1动力计算参数

动力分析中桥梁阻尼采用Rayleigh阻尼，阻尼比取为2.0%。

本次仿真车辆采用CRH2型车，16辆编组，仿真车速为90～200 km/h。轨道不平顺谱采用美国六级谱，典型样本如图5所示，具体工况见表3。

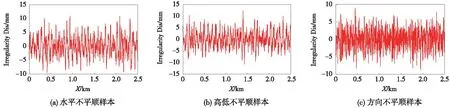
图5　典型轨道不平顺样本

最高运营车速/(km/h)车型车速/(km/h)200CRH290、110、120、140、160、180、200 编组16辆2×(1拖+2动+2拖+2动+1拖)轨道不平顺美国六级谱

4.220 m跨度梁动力仿真分析结果

20 m梁选取梁高1.10 m、1.15 m两种梁型，仿真分析结果如表4所示。从车辆响应结果可以看出，两种计算梁高在所有计算车速下，车辆响应均满足相关规范要求，舒适性优秀。

从结构响应看，对照20 m跨简支梁实际荷载效容许动力放大系数可得，仿真计算中各运行车速下的动力放大系数为1.470，小于容许值2.391，满足设计荷载效应大于实际荷载效应原则，结构安全。

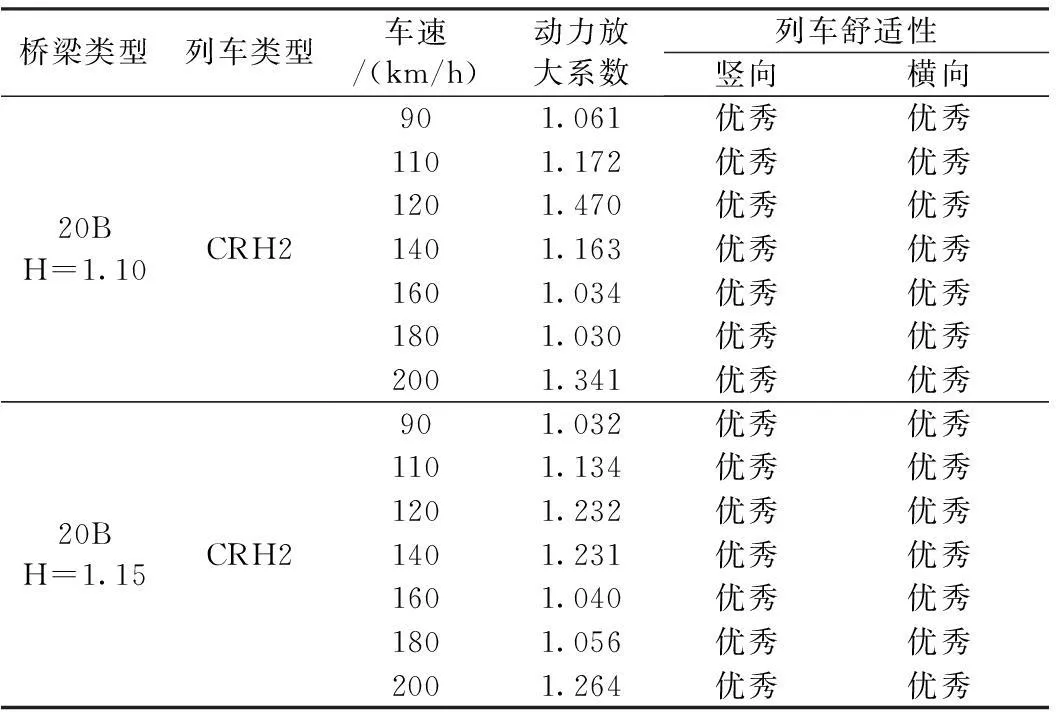
表4　20 m梁动力仿真结果

取1.10 m梁高仍能保证设计的安全合理，由此所取频率限值为f0=77.80/L，该频率限值略小于UIC限值。

4.324 m跨度梁动力仿真分析结果

24 m梁选取梁高1.35 m、1.40 m两种梁型，仿真分析结果如表5所示。从车辆响应结果可以看出，两种计算梁高在所有计算车速下，车辆响应均满足相关规范要求，舒适性优秀。

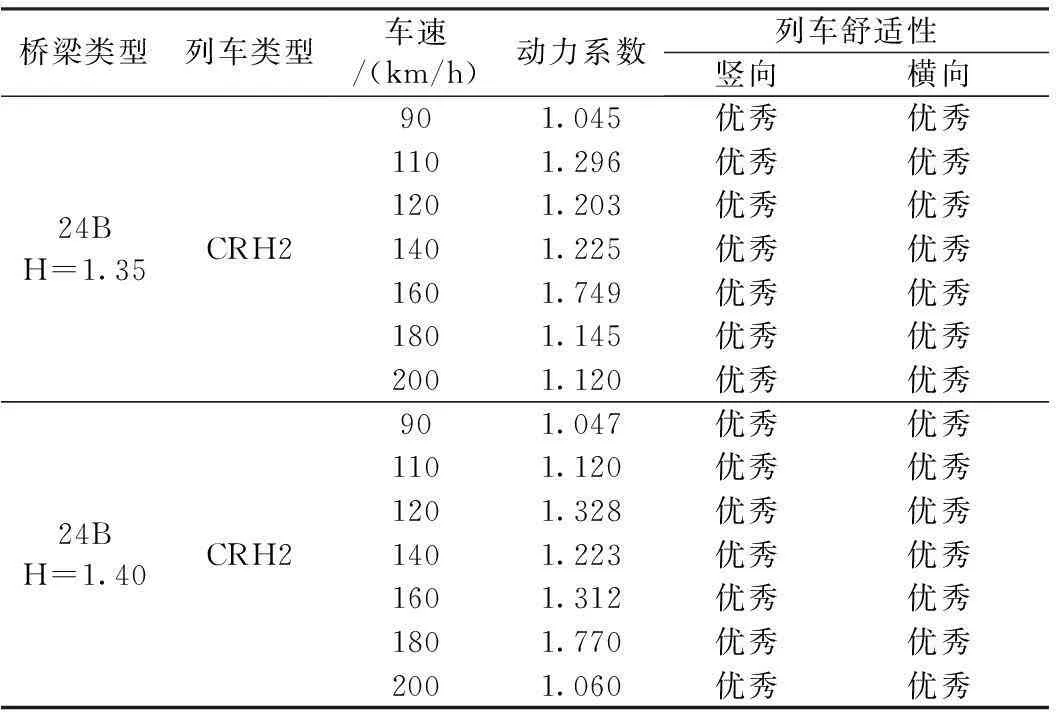
表5　24 m梁动力仿真结果

从结构响应看，对照24 m跨简支梁实际荷载效容许动力放大系数可得，仿真计算中各运行车速下的动力放大系数为1.770，小于容许值2.428，满足设计荷载效应大于实际荷载效应原则，结构安全。

取1.35 m梁高仍能保证设计的安全合理，由此所取频率限值为f0=22.64L-0.592，该频率限值略小于UIC限值。

4.432 m跨度梁动力仿真分析结果

32 m梁选取梁高1.90 m、1.95 m两种梁型，仿真分析结果如表6所示。从车辆响应结果可以看出，两种计算梁高在所有计算车速下，车辆响应均满足相关规范要求，舒适性优秀。

从结构响应看，对照24 m跨简支梁实际荷载效容许动力放大系数可得，仿真计算中各运行车速下的动力放大系数为1.737，小于容许值2.604，满足设计荷载效应大于实际荷载效应原则，结构安全。

取1.90 m梁高仍能保证设计的安全合理，由此所取频率限值为f0=22.33L-0.592，该频率限值略小于UIC限值。

综合三种常用跨度简支箱梁的动力仿真结果可以看出：当城际梁梁高取值较小，与之对应的竖向基频略小于UIC频率限值时，结构的动力响应依然较小，列车动行舒适性较好。说明常用跨度城际梁取用UIC规定的频率限值要求能够满足要求，且有一定的富余。

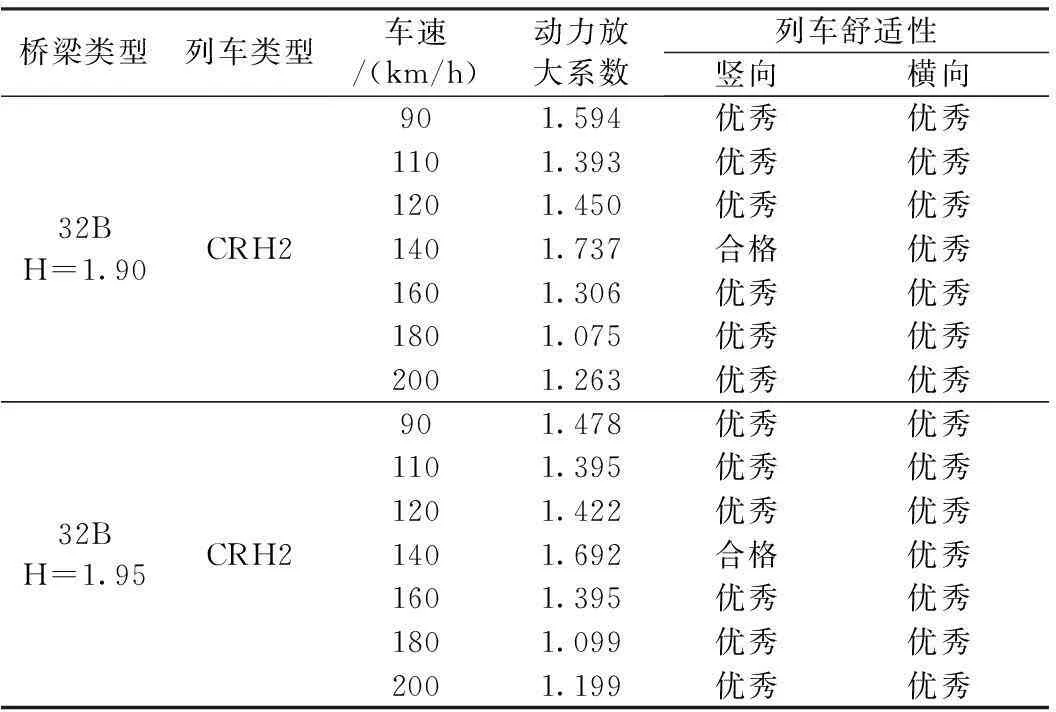
表6　32 m梁动力仿真结果

5结论

(1)根据目前城际梁设计相关资料，拟定城际铁路常用跨度简支箱梁的截面尺寸，建立有限元模型，进行结构的竖向基频计算，根据设计荷载效应大于等于实际运营车辆荷载效应的原则，得出各跨度简支梁实际运营车辆最大允许动力系数。

(2)应用车辆-桥梁耦合分析理论，通过动力仿真，计算各跨度简支梁在实际运营车辆下的动力响应，通过比较得出，按照国际铁路联盟规定的桥梁结构的频率下限值设计，能够满足结构安全及使用舒适性的要求。

参考文献

[1]Code，UIC. Track/bridge Interaction recommendations for calculations. UIC774-3，2001

[2]日本铁道综合技术研究所.日本铁路结构设计标准和解释-混凝土结构[R].东京：日本铁道综合技术研究所，2004

[3]高策.城际铁路双线圆端形实体桥墩设计研究[J].铁道勘察，2013(2):86-89

[4]邓运清.高速铁路简支箱梁设计研究[J].铁道标准设计，2004(7):125-129

[5]邓运清.客运专线简支箱梁综述[J].铁道工程学报，2005(2):65-71

[6]侯建军.客运专线简支箱梁四支点平整度分析及施工控制[J].铁道勘察，2012(2):89-92

[7]国家铁路局.城际铁路设计规范[S].北京：中国铁道出版社，2015

[8]简方梁.大型站房结构动力响应分析研究[D].上海:同济大学，2012

[9]李奇.车辆—桥梁/轨道系统耦合振动精细分析理论及应用[D].上海:同济大学，2008

[10]翟婉明.车辆-轨道垂向系统的统一模型及其耦合动力学原理[J].铁道学报，1992，14(3):10-21

[11]雷晓燕.列车通过轨道不平顺和刚度突变时对轨道振动的影响[J].铁道科学与工程学报，2005，6(2):1-8

[12]雷晓燕.移动荷载作用下轨道基础刚度突变对轨道振动的影响[J].振动工程学报，2006，19(2):195-199

收稿日期：2016-02-26

基金项目：国家铁路局科技研究项目(KF2014-052)

第一作者简介：简方梁(1982—)，男，2012年毕业于同济大学桥梁工程专业，工学博士，高级工程师。

文章编号：1672-7479(2016)03-0101-04

中图分类号：U238; U441+.3

文献标识码：B

Research on the Fundamental Frequency Limits of Simply-Supported Box Beams with Commonly-Used Spans Applied on Intercity Railway

JIAN FangliangXU ShengqiaoTIAN Yang