柔性Job Shops集成调度启发式算法

周炳海, 赵　猛

(同济大学 机械与能源工程学院,上海 201804)



柔性Job Shops集成调度启发式算法

周炳海, 赵猛

(同济大学 机械与能源工程学院,上海 201804)

摘要:为有效解决柔性作业车间(Job Shops)的加工与搬运集成调度问题,以最小化最大完工时间(Makespan)为调度目标,建立非线性规划模型,提出基于贪婪启发式策略的变邻域搜索算法(GRS-RVNS).根据准时(JIT)生产和均衡生产思想构建贪婪启发式策略快速求初始解.利用析取图表示可行解并根据析取图调度的性质定理构建有效的搜索邻域,进而利用随机变邻域搜索算法对初始解进行优化.对提出的算法进行仿真实验分析,结果表明：该算法求解时间短、调度方法有竞争性.

关键词：搬运；柔性作业车间(Job Shops)；调度；启发式算法；变邻域搜索算法(RVNS)

柔性作业车间(Job Shops)是经典Job Shops的扩展,适合实际生产中多品种小批量的生产模式.近来,柔性Job Shops中逐渐引入自动化搬运设备,提高了生产效率的同时也引发了复杂度更高的加工与搬运集成调度问题.但是,目前关于柔性Job Shops调度问题的研究绝大多数仅考虑加工工序而未考虑搬运工序.因此,对柔性作业车间中加工和搬运工序的集成调度问题进行研究具有重要的现实与理论意义.

考虑搬运的Job Shops调度问题可分为2类.第一类是带一个搬运设备Job Shops调度问题,该问题需要对机床和搬运设备同时调度.Hurink等[1]将单个运输设备视作含Set-up时间的机床,提出了禁忌搜索算法对问题求解.Brucker等[2]针对问题建立混合整数规划模型并用CPLEX求解.第二类是带多个搬运设备的Job Shop调度问题,该类问题与前类问题相比还需考虑搬运设备指派问题.针对该类问题目前文献多采用元启发式算法,如:改进蜜蜂群算法[3]、改进型遗传算法[4]、局域搜索算法[5]、禁忌搜索算法[6]、模拟退火算法及局域搜索的混合算法[7]等求解问题.Lacomme等[8]针对该问题提出了调度框架并设计了文化基因算法.

考虑搬运的柔性作业车间调度问题的复杂度更高,其调度任务包括为加工工序和搬运工序分别指派机床和搬运设备、确定工件在机床及搬运设备上的排序.Zhang等[9]针对该问题提出改进转换瓶颈算法,实验结果表明算法能够求得较优解,但是算法采用随机方式为加工工序指派机床,这致使运算比较耗时.Zhang等[10]针对该问题设计的结合遗传算法和禁忌搜索算法的混合算法求解效果较好,但其随机生成的初始解的质量有待提高.Liu等[11]针对该问题设计了微型蜜蜂群算法并尝试求解大规模算例.

本文在上述研究的基础上,针对考虑搬运的柔性作业车间调度问题建立数学模型并分析问题特点构造基于贪婪策略的变邻域搜索算法(greedy heuristic strategy-random variable neighborhood searchalgorithm, GRS-RVNS)(变邻域搜索算法(RVNS)能较好地求解组合优化问题[12-14]),旨在尝试综合利用构造型启发式算法的快速求解优势与搜索算法的强寻优能力优势求解所研究问题,并通过仿真实验验证算法的有效性.

1问题描述与建模

Oi,jOi,j+1…Oi,ni.

其中,Oi,jTi,j表示Oi,j在Ti,j之前.调度任务是在满足各种资源约束和工艺路线关系约束的前提下,为每道加工工序和搬运工序指派最合适的机床和搬运设备,确定每台机器和每个搬运设备上各道工序的最佳加工顺序以及开工时间使总完工时间(Makespan)Cmax最小.

作如下假设：1)机床的输入和输出缓存区足够大,不会引起阻塞；2)单个机床的加工能力和单个搬运搬运设备的搬运能力均为1；3)同一工件一次只能占用一台机床或一个搬运设备；4)所有工件和资源在调度开始时刻均处于可调度状态,不考虑宕机.

据笔者所收集的文献资料,该调度问题的数学模型较为鲜见.本文基于以上定义,分析问题特点及约束关系,建立如下数学模型：

minCmax.

(1)

s.t.

(2)

(3)

∀j∈[1,ni-1],∀R∈{R1，R2，…，Rr}.

(4)

∀i,i′∈[1,n],∀j,j′∈[1,ni],

∀j′∈[1,ni′],∀M∈{M1,M2，…，Mm}.

(5)

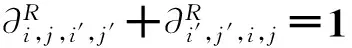
∀j′∈[1,ni′-1],∀R∈{R1,R2，…，Rr}.

(6)

(7)

∀i,i′∈[1,n],∀j∈[1,ni],∀j′∈[1,ni′],

∀M∈{M1,M2，…，Mm}.

(8)

(9)

∀i,i′∈[1,n],∀j∈[1,ni-1],∀j′∈[1,ni′-1],

∀R∈{R1,R2，…，Rr}.

(10)

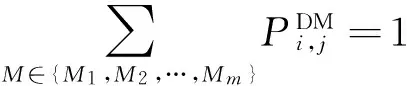
(11)

∀j∈[1,ni-1].

(12)

其中,式(1)表示调度目标最小化最大完工时间最优,式(2)表示最小化最大完工时间大于等于各工件的尾工序的结束时间,式(3)表示工件完成加工之后才能开始搬运,式(4)表示工件运输到机床之后才能开始加工,式(5)表示一台机床一次只能加工一个工件,式(6)表示一个搬运设备一次只能搬运一个工件,式(7)和(8)分别表示同一机床M上的2个加工工序之间的满足先后顺序关系,式(9)和(10)分别表示同一搬运设备R完成的2个搬运工序之间满足先后顺序关系,式(11)表示一个工件一次只能分配到一台机床加工,式(12)表示一个工件一次只能由一台搬运设备完成搬运.

析取图可直观地表述可行解,一个包含3个工件、4台机床、2个搬运设备的柔性作业车间调度问题的可行解用析取图表示,如图1所示.析取图中从起点s到终点e的最长路径为关键路径,其长度可以利用图论中的关键路径算法[15]计算,关键路径的长度等于最小化最大完工时间.

图1　可行解的析取图表示Fig.1　Disjunctive graph for representation of feasible solutions

2算法构建

为解决考虑搬运的柔性作业车间调度问题,设计一个基于贪婪启发式策略的变邻域搜索算法(GRS-RVNS).贪婪策略首先基于准时化生产(just in time, JIT)生产和平衡生产思想定义机床和搬运设备的复合指派系数,同时为了使工序尽可能早地开始加工且不影响其他工序,提出基于位置检测的插入与追加综合法计算工序的开始时间.在贪婪策略求得初始解之后,用析取图表示可行解并根据析取图调度的性质定理构建有效的搜索邻域,最后结合变邻域搜索算法对初始解进行优化.

2.1贪婪启发式策略

JIT生产能够使工件尽早完成以缩短制造周期,而生产中资源利用越平衡越能削弱瓶颈资源对制造工期的不良影响,据此定义机床和搬运设备的复合指派系数.

定义1机床指派系数：

ΘM=w1ξ1+w2ξ2.

式中:

为JIT水平指标(若机床M尚未分配加工任务则ξ1=0),该值越小表征工件越能及时加工；

表示当前调度时刻机床的负载率,该值越小表征机床M的当前负载率越低.w1和w2为权重系数,满足w1+w2=1.

定义2搬运设备指派系数：

ΘR=w3ξ3+w4ξ4.

式中:

为JIT水平指标(若搬运设备R尚未分配搬运任务则ξ3=0),该值越小表征工件越能及时被搬运；

表示当前调度时刻搬运设备的负载率,该值越小表征机床R的当前负载率越低.w3和w4为权重系数,满足w3+w4=1.

工序的开始时间直接影响调度目标,为了使工序尽可能早地开始加工且不影响其他工序,提出基于位置检测的插入与追加综合法计算工序的开始时间.首先检测同一机床或搬运设备的已调度工序之间是否有合适的位置可以插入待调度工序,如果位置不存在,则利用追加法计算工序开始时间,否则,利用插入法计算工序开始时间.综合方法定义如下.

定义3设OM中工序排序为{O1,O2,…,Oλ,…,Oλe},appendOrInsert(Oi,j,M)定义如下.令

}.

否则用插入法计算,令

定义4设OR中工序排序为{T1,T2…Tβ…Tβε},appendOrInsert(Tij,R)定义如下：令

否则用插入法计算,令

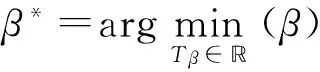
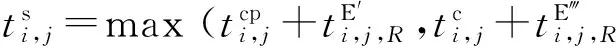
2.2邻域结构

变邻域搜索算法在求解过程中根据某种优化机制动态地改变邻域结构,从而避免陷入局部最优而向全局最优靠近,邻域搜索结构的优劣是影响算法结果的重要因素.本文基于可行解的析取图表示,定义机床块MBlock为关键路径Ps上连续的由同一台机床加工的工序,搬运块RBlock为Ps上连续的由同一个搬运设备完成的搬运工序,基于文献[1]提出的析取图调度的性质定理构造以下4种邻域.

定义5将SwapOnMBlock(s)记作N1(s),将MBlock内的非首工序与前道工序交换直至其与首工序交换或者将非尾工序与后道工序交换直至其与尾工序交换.例如：若

MBlock=(Oi,j,Oi′,j′,Oi″,j″),则

N1(s)={(Oi′,j′,Oi,j,Oi″,j″),(Oi″,j″,Oi,j,Oi′,j′),(Oi,j,Oi″,j″,Oi′,j′),(Oi′,j′,Oi″,j″,Oi,j)}.

定义6将ExtraExchangeOnRBlock(s)记作N2(s),将RBlock内非首工序与首工序交换或者将非尾工序与尾工序交换.例如,若

RBlock=(Ti,j,Ti′,j′,Ti″,j″),则

N2(s)={(Ti′,j′,Ti,j,Ti″,j″),(Ti″,j″,Ti′,j′,Ti,j),(Ti,j,Ti″,j″,Ti′,j′)}.

定义7将InnerExchangeOnRBlock(s)记作N3(s),随机交换RBlock内的2个非首尾工序.例如：若

RBlock=(Ti0,j0,Ti,j,Ti′,j′,Ti″,j″),则

N3(s)={(Ti0,j0,Ti′,j′,Ti,j,Ti″,j″)}.

定义8将Equilibrium(s)记作N4(s),为关键路径上的加工工序重新指派负载率较低的可加工机床或为关键路径上的搬运工序重新指派负载率较低的可搬运设备.

在邻域搜索的过程中,遍历当前邻域选出局部最优解与初始解对比,若局部最优解优于初始解,则以该局部最优解替换初始解,并以其作为出发点继续在当前邻域进行搜索；否则跳到下一个邻域进行搜索,直到满足停止准则.

2.3算法描述

基于以上定义,本文构造的算法详细描述如下.其流程图如图2所示.

步骤1确定可调度加工工序集：

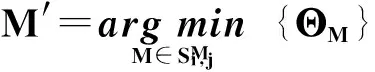
步骤3令

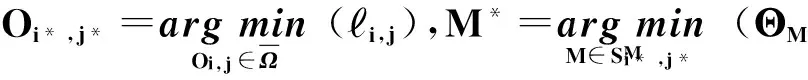
步骤4执行appendOrInsert(Oi*,j*,M*)

图2　邻域搜索算法流程图Fig.2　Flow chart of neighborhood search algorithm

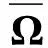
步骤8确定可调度搬运工序集：

∀i∈[1,n],∀j∈[1,ni-1]}.

步骤10令

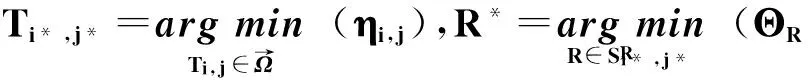
步骤11执行appendOrInsert(Ti*,j*,R*).

步骤13更新相关加工工序的开始时间.

步骤16变邻域搜索(其中，k为领域结构的序号)：

1)初始化k=1；

2)若达到停止准则,则转步骤17；否则,执行以下步骤；

3)随机在Nk(s)中选择x；

4)遍历搜索x的邻域Nk(x)中最好的解x′；

5)若Cmax(x′)

步骤17算法终止输出所求解.

3仿真实验

引入变量差距1：

引入变量差距2：

本文算法参数设置如下：w1、w3服从区间[0,1]上的均匀分布,w2和w4分别满足w1+w2=1与w3+w4=1约束关系,在实验过程中根据算法流程对2组参数(w1,w2)和(w3,w4)分别随机产生10组不同的参数组合,以局部结果最优为依据确定最优参数值.邻域搜索顺序也是影响变邻域搜索算法的因素之一,为了避免重复某一个邻域搜索顺序,采用随机变邻域搜索策略,即在搜索过程中设置搜索步长Step服从区间[1,kmax]的均匀分布,算法终止条件为连续10次迭代运算结果无改善,实验结果如表1所示.其中INST4类算例的第四列数据为利用文献[9]中算法随机指派机床的单次运算结果,第六列数据为利用文献[9]中算法多次运算的最好结果.

表1本文算法与其他3种算法求解算例Makespan的结果对比

Tab.1Results comparison of Makespan by our algorithm and other three algorithms

算例MSB[9]GRSGTSGRS-RVNS1P01D1d115614998[10]1002P01D1t1939489[10]893P01T2t1939581[10]814P01T3t0959894[10]945P01D3d1224233220[10]2196P01D2d1158162158[10]1587PL01585854[5]568PL02656845[5]469PL03747045[5]4510PL04858645[5]4511EX119710096[10]9712EX12828682[10]8213EX13888884[10]8614EX14110112103[10]10615EX21109112103[10]10316EX22808376[10]7617EX23879186[10]8618EX24126129108[10]10819EX3111011299[10]9920EX32878985[10]8421EX33898986[10]8622EX34136135115[10]11523FJSP1173016901599[9]159424FJSP2167816521549[9]153225FJSP3109610991061[9]106026FJSP4111310961027[9]103127FJSP5141914031308[9]130828FJSP6140214171339[9]132529FJSP7141013661292[9]129130FJSP8146114501350[9]135031FJSP9158815911567[9]157432FJSP10201519981871[9]1871

3.1GRS运算时间分析

在求解规模为100的算例用时约4 s,总体来看算法求解时间较短,适用于生产动态中的实时调度.

3.2GRS运算结果分析

根据表1统计各算例的Gap1值绘制图3,观察图3可知对于前3类算例Gap1值大多数为正值,而第4类算例的多为非正值,4类算例的Gap1均值依次为1.41%、0.10%、2.22%、-0.97%,表明对前3类问题GRS与文献[9]中MSB算法相比求解结果没有优势,而对于INST4类算例求解具有明显优势.这是因为前3类实例均为不含机床指派问题,第四类实例INST是包含机床指派的柔性作业车间调度问题,而算法MSB采用的随机指派机床的方式无法有效解决机床指派问题,因此对结果造成不良影响.在运算时间方面GRS和MSB的最长用时约为15 s和600 s,综合考虑运算时间和求解结果,GRS能够在较短的时间内求解带搬运设备的作业车间调度问题.

图3　各算例差距1值对比分析Fig.3　Comparison of Gap1 values of each instance

图4　ILS与GRS-VNS算法收敛性比较Fig.4　Convergence comparison for ILS and GRS-VNS algorithms

3.3GRS-RVNS算法收敛性分析

以算例9为例考察GRS-RVNS算法收敛性,并与文献[5]中的ILS算法作对比如图4所示.

可知本文算法在迭代约70次就得到最优解,而ILS算法需要迭代约120次才得到最优解,可见本文算法收敛速度较快,这说明本文构造邻域结构及变邻域搜索方法是有效的.

3.4GRS-RVNS算法运算结果分析

图5　各类算例非正差距2值比例Fig.5　Non-positive Gap2 values’proportion for each kind of instances

根据表1统计各算例的Gap2值绘制图5,可知Gap2值在区间[-1.18%, 3.70%]内变化,4类算例的Gap2均值依次为0.26%、1.48%、0.43%、-0.18%,可见本文算法运算结果与参照算法运输结果非常接近.但是Gap2正值和非正值的出现波动较大,为进一步分析运算结果,统计各类算例非正Gap2值所占比例绘制图5.图5表明4类算例分别有83%、50%、75%、80%的运算结果不比参照算法所求结果差.总体来看本文构建的算法对求解带搬运设备的柔性作业车间调度问题是有效的.

3.5搬运设备数量对算法的影响

算例7、8、9、10所含的工件数和机床数相同(即搬运任务数量相同),搬运设备数依次为1、2、3、4,统计GRS-RVNS算法求解各算例结果绘制图6.可知当搬运任务数量一定时,随着搬运设备的增多总完工时间呈减小趋势.当搬运设备达到一定的数量之后,搬运设备数目对总完工时间影响不大.据此可以利用本文算法为生产车间配置合理的搬运设备数目提供理论依据.

图7　搬运设备数量对GRS-VNS算法的影响Fig.7　Influence of number of handling equipment on GRS-VNS algorithm

4结语

本文建立了柔性作业车间的加工与搬运集成调度问题的数学模型,尝试利用构造型启发式算法与变邻域搜索算法的综合优势求解问题,为此类问题的求解提供新思路.实验结果表明：基于JIT生产和均衡生产思想构建的贪婪启发式策略能够快速有效地求解所研究问题；基于可行解的析取图表示方式构建的搜索邻域及随机变邻域搜索算法是有效的,且该算法有较好的收敛性.本文算法还可以为生产车间配置合理的搬运设备数目提供理论依据.

参考文献(References)：

[1] HURINK J, KNUST S. Tabu search algorithms for job-shop problems with a single transport robot [J]. European Journal of Operational Research, 2005, 162(1): 99-111.

[2] BRUCKER P, BURKE E K, GROENEMEYER S. A mixed integer programming model for the cyclic job-shop problem with transportation [J]. Discrete Applied Mathematics, 2012, 160(13): 1924-1935.

[3] LEI D, GUO X. Scheduling job shop with lot streaming and transportation through a modified artificial bee colony [J]. International Journal of Production Research, 2013, 51(16): 4930-4941.

[4] CHAUDHRY I A, MAHMOOD S, SHAMI M. Simultaneous scheduling of machines and automated guided vehicles in flexible manufacturing systems using genetic algorithms [J]. Journal of Central South University of Technology, 2011, 18(5): 1473-1486.

[5] LACOMME P, LARABI M, TCHERNEV N. A disjunctive graph for the job-shop with several robot [C] ∥MISTA Conference. Paris: MISTA, 2007: 285-292.

[6] ZHENG Y, XIAO Y, SEO Y. A tabu search algorithm for simultaneous machine/AGV scheduling problem [J]. International Journal of Production Research, 2014,52(19): 5748-5763.

[7] DEROUSSI L, GOURGAND M, TCHERNEV N. A simple metaheuristic approach to the simultaneous scheduling of machines and automated guided vehicles [J]. International Journal of Production Research, 2008, 46(8): 2143-2164.

[8] LACOMME P, LARABI M, TCHERNEV N. Job-shop based framework for simultaneous scheduling of machines and automated guided vehicles [J]. International Journal of Production Economics, 2013, 143(1): 24-34.

[9] ZHANG Q, MANIER H, MANIER M A. A modified shifting bottleneck heuristic and disjunctive graph for job shop scheduling problems with transportation constraints [J]. International Journal of Production Research, 2014, 52(4): 985-1002.

[10] ZHANG Q, MANIER H, MANIER M A. A genetic algorithm with tabu search procedure for flexible job shop scheduling with transportation constraints and bounded processing times [J]. Computers and Operations Research, 2012, 39(7): 1713-1723.

[11]LIUZ,MAS,SHIY,etal.Solvingmulti-objectiveflexibleJobShopschedulingwithtransportationconstraintsusingamicroartificialbeecolonyalgorithm[C] ∥ 2013IEEE17thInternationalConferenceonComputerSupportedCooperativeWorkinDesign(CSCWD).Whistler：IEEE, 2013: 427-432.

[12]DRIESSELR,MÖNCHL.Variableneighborhoodsearchapproachesforschedulingjobsonparallelmachineswithsequence-dependentsetuptimes,precedenceconstraints,andreadytimes[J].ComputersandIndustrialEngineering, 2011, 61(2): 336-345.

[13]MLADENOVIN,TODOSIJEVIR,UROEVID.TwolevelGeneralvariableneighborhoodsearchforAttractivetravelingsalesmanproblem[J].ComputersandOperationsResearch, 2014, 52(1): 341-348.

[14]MLADENOVIN,TODOSIJEVIR,UROEVID.Lessismore:Basicvariableneighborhoodsearchforminimumdifferentialdispersionproblem[J].InformationSciences, 2016, 326: 160-171.

[15] 严蔚敏, 吴伟民. 数据结构:C语言版 [M].北京：清华大学出版社有限公司,2002.

[16]BILGEÜ,ULUSOYG.AtimewindowapproachtosimultaneousschedulingofmachinesandmaterialhandlingsysteminanFMS[J].OperationsResearch, 1995, 43(6): 1058-1070.

收稿日期：2015-02-28.

基金项目：国家自然科学基金资助项目(71471135，61273035)；国家“863”高技术研究发展计划资助项目(2009AA043000).

作者简介：周炳海(1965—), 男, 教授, 博导，从事离散制造系统维护、调度、建模与仿真研究.ORCID: 0000-0002-6599-9033. E-mail: bhzhou@tongji.edu.cn

DOI:10.3785/j.issn.1008-973X.2016.06.009

中图分类号：TP 29

文献标志码：A

文章编号：1008-973X(2016)06-1073-07

Hybrid heuristic algorithm for integrated scheduling in flexible Job Shops

ZHOU Bing-hai, ZHAO Meng

(SchoolofMechanicalEngineering,TongjiUniversity,Shanghai201804,China)

Abstract:The non-linear programming model was developed with an objective of minimizing system Makespan to solve the integrated scheduling problem of processing and handling in flexible job shops effectively. A greedy heuristic strategy based variable neighborhood search algorithm (GRS-RVNS) was put forward. The greedy heuristic strategy was designed with the combination of the just in time (JIT) and balanced production ideas, in order to get initial solution rapidly. An effective neighbor was constructed based on the disjunctive graph representations of the feasible solutions and properties and theorems of the disjunctive graph scheduling. The neighbor was used in the random variable neighborhood search algorithm. Finally, the experiments were designed for the proposed algorithm. Results indicate that the computing time of the proposed algorithm is short and the scheduling method is promising.

Key words:handling, flexible job shops, scheduling, heuristic algorithm, variable neighborhood search algorithm