基于行星际/太阳风和地磁条件的紫外极光卵边界建模和预测
2016-07-28杨秋菊胡泽骏韩德胜胡红桥马骁
杨秋菊, 胡泽骏, 韩德胜, 胡红桥, 马骁
1 陕西师范大学 物理学与信息技术学院,西安 710119 2 中国极地研究中心 国家海洋局极地科学重点实验室, 上海 200136
基于行星际/太阳风和地磁条件的紫外极光卵边界建模和预测
杨秋菊1, 胡泽骏2*, 韩德胜2, 胡红桥2, 马骁1
1 陕西师范大学 物理学与信息技术学院,西安710119 2 中国极地研究中心 国家海洋局极地科学重点实验室, 上海200136
摘要极光卵的尺度大小与太阳风-磁层-电离层能量耦合过程紧密相关,准确预测其大小对空间天气研究和预报具有非常重要的意义.本文基于模糊c均值聚类算法,从Polar卫星紫外极光图像中自动提取极光卵边界数据(~1215000个赤道向边界点和~3805000极向边界点),统计分析其与太阳风等离子体、行星际磁场、地磁指数等之间的相关特性,并构建了以行星际、太阳风为模型参数(模型1)和以行星际、太阳风及地磁指数为模型参数(模型2)的2种极光卵边界多元回归模型.以模型预测的极光卵边界与实际极光卵边界之间的平均绝对误差作为模型评价标准,将本文预测模型与Carbary(2005)模型和Milan(2009)模型进行了对比.结果表明,模型2对极光卵极向、赤道向边界预测的平均绝对误差为1.55和1.66地磁纬度,优于Carbary和Milan模型(Carbary模型极向、赤道向边界的平均绝对误差为2.18和5.47地磁纬度,Milan模型极向、赤道向边界的平均绝对误差为1.71地磁纬度和1.90地磁纬度).
关键词紫外极光; 极光卵边界; 行星际地磁环境; 回归分析
1引言
极光卵是极光粒子沉降以磁极为中心在地球南北极地区形成的椭圆带状区域,是地球上来自太阳的能量粒子的影响区域.极光卵能从全局尺度上对空间天气进行表征和预测,所以一个好的极光卵模型能有效地帮助理解空间天气并预测其对极区和次极区的影响(Carbary, 2005).在过去的几十年里,学者们就如何利用空间参数来描述极光卵已经开展了广泛的研究(Carbary, 2005; Zhang and Paxton, 2008; Holzworth and Meng, 1975, 1984; Kauristie, 1995; Sigernes et al., 2011a, 2011b; Starkov, 1994),具体的研究工作可以分为以下两大类:
第一类是利用单变量回归分析的方法,其中回归量常常取某一个地磁指数.比如,在文章(Holzworth and Meng, 1975; Starkov, 1969)中,极光卵边界位置被近似描述成磁地方时和地磁指数Q的函数;Starkov(1994)曾将极盖大小的变化、极光卵和弥散极光分别估计成AL指数(表征极光电集流下包络线最小扰动)的函数;在每个亚暴阶段,对每个预设定的极光电集流AE指数,Kauristie(1995)提出将极光卵边界拟合成局部时间的函数;Carbary(2005)曾将每个磁地方时处的极光卵极向边界,赤道向边界以及峰值都拟合成Kp指数的线性函数;Sigernes等人(2011b)比较了(Zhang and Paxton, 2008)和(Starkov, 1994)两文中的方法,它们都通过Kp指数的函数来计算极光卵的大小和位置.
然而,从物理源头来说,这些地磁活动指数(Q, AE,Kp, AL等)与极光是同一级的物理量:它们都受太阳风-磁层-电离层耦合作用的影响.换句话说,这些地磁活动指数仅仅能从一个侧面来反映极光卵的属性,因为它们都受同一个“源”的影响,但并非因果关系.因此,第二类研究工作主要集中于从引发极光卵变化的源头来研究极光卵的变化:即采用多变量回归分析方法,研究极光卵对太阳风等离子体和行星际磁场(IMF)参数的依赖性.比如,Cho等人(2010)探讨了磁层被行星际激波冲击时极光卵夜侧极向边界的纬度变化;Holzworth and Meng (1984)研究了150幅极光图像,将所有磁地方时作为一个整体考虑,将极光卵边界拟合成一个椭圆,椭圆的大小被估计为IMFBz分量的线性函数;更为常见的情况是,通过考虑不同IMF的方向,IMF分量被用来进行定性分析(如Bz>0和Bz<0分开讨论)(Brittnacher et al., 1999; Liou et al., 1998);Milan等人(2010)利用IMAGE卫星数据,把Kp指数、IMF、太阳风参数按大小进行分段,分别讨论每个参数对极光卵亮度、形状的影响.事实上,极光活动是受所有行星际参数共同影响的,传统的一元回归分析或定量分析的方法不能充分表征极光卵的变化.鉴于地球环电流也被证实与极光卵半径密切相关(Huang et al., 2009; Milan et al., 2009),Milan (2009)首次将行星际条件和环电流结合在一起,采用多元回归分析的方法研究其对极光卵半径的影响.
Kauristie(1995)曾指出,使用卫星图像是同时确定整个(或绝大部分)极光卵边界的唯一途径.本文利用Polar卫星的UVI极光图像数据来研究极光卵边界在不同空间环境下的变化.因为从大量的UVI图像中人工确定极光卵边界是非常繁琐的而且效率很低,本文借助于计算机自动图像分割技术.我们前期的工作(王倩等,2011)已经证实模糊聚类技术是分割极光卵边界的一种有效方法,而且通过把从DMSP卫星中获得的粒子沉降边界作为基准,发现模糊聚类方法分割得到的极光卵边界优于之前的方法.
基于Polar卫星海量极光图像数据,本文将通过多元回归分析的方法来研究极光卵边界位置的变化,获得的回归模型能给空间天气预测提供有用信息.在模型参数的选取方面,本文首先考虑IMF三分量变化对极光卵的影响.因为IMF尤其是IMFBz分量能控制极光卵的位置已被广泛认识(Holzworth and Meng, 1975; Hardy et al., 1981),不同的IMF条件会使得极光卵转向不同的方向(Cowley et al., 1991; Liou et al., 2001; Meng, 1980).第二,除了IMF外,太阳风,特别是太阳风动压,能显著地影响地球磁场,从而影响极光卵边界的位置(Yang et al., 2013; Lee et al., 2004; Lyons, 2000; Hu et al., 2009, 2010, 2012, 2013, 2014).绝大多数之前的研究都把太阳风动压作为一个整体对待来研究其与极光亮度的关系,可Shue等人(2002)统计发现太阳风密度和速度是单独作用于极光亮度的(Yang et al., 2013),因此在本文的回归模型中,太阳风动压、速度、密度都被考虑进来.第三,IMF和太阳风只反映了日侧极光动力学过程,而极光电集流指数(AE)与大的地磁活动比如磁暴或亚暴紧密相关(Kauristie, 1995),因而能反映夜侧极光卵的边界情况.基于上述考虑,本文建立了两个极光卵预测模型.在第一个模型中,只考虑用简单的一次多项式来对IMF、太阳风的6个行星际参数进行回归分析.在第二个模型中,我们只考虑独立参量,把与太阳风速度和密度紧密相关的太阳风动压参量去掉,换成与夜侧极光紧密相关的地磁指数AE.因为每个磁地方时处极光卵的变化规律都不一样,本文将针对每个磁地方时分别进行建模分析.模型结果将与两种有代表性的模型进行对比:第一类研究中典型的Kp模型(Carbary, 2005),第二类研究中性能表现非常好的Milan(2009)模型.
综上,本文基于1996年12月至1999年1月的3个冬季6万多幅Polar卫星紫外极光图像,讨论2种基于行星际和地磁参数的极光卵边界预测方法,根据行星际和地磁环境对所有24个磁地方时处的极向、赤道向极光卵边界的地磁纬度进行估计.具体实现步骤包括:UVI图像预处理、极光卵边界自动分割、行星际和地磁参数获取、数据集构建、回归建模、极光卵边界位置预测及预测结果评价.本文的研究可以用于空间天气研究中对极光卵边界位置的预测.
2数据集构建
2.1数据来源及简介
Polar卫星上的UVI能同时观测到日侧和夜侧的极光图像,并返回了大量北半球极光图像.本文涉及1996年12月至1999年1月的3个冬季(共6个月,183天)的极光图像,因为在这些月份里,日辉效应带来的不利影响可以基本忽略.和之前很多研究一样,本文也仅使用LBH的长波段数据(~170 nm).普通观测模式下两帧连续图像之间的时间间隔基本上都在0.5~3 min之间,图像大小为200×228像素.
本文所使用的IMF三分量,太阳风密度、速度和动压,以及地面观测指数AE、环电流测度Sym-H指数,均从NASA OMNI数据中获得,时间分辨率为1 min.因为OMNI数据在磁层顶给出,我们需要考虑在电离层看到极光现象时经历的延迟时间.这个延迟时间估计为穿越磁鞘的5 min延迟和到达电离层的2 min Alfven分波传送时间之和(Yang et al., 2013; Liou et al., 1998).
2.2极光卵边界自动分割
在极光卵边界自动分割之前,本文先对高噪声的UVI图像进行了预处理操作(杨秋菊等,2013),包括移除低纬区域、用椭圆形状截取原图、负值点清零、图像平滑等.图1b是图1a所示的极光原始图像预处理后的结果.我们之前的工作已经证实模糊c均值聚类方法是分割模糊极光卵边界的有效方法(王倩等,2011).在本文中,一种包含空间信息的模糊c均值聚类方法(SFCM)(Chuang et al., 2006)被用来分割UVI图像的极光卵边界.在分析了大量UVI图像后,本文最终决定将每幅UVI图像聚类成6类(图1c).根据聚类结果,强度最小的两个或三个聚类簇被视为背景,其他则为极光卵区(图1d).因为聚类过程是基于亮度强弱进行的,所以经常会出现图像中一些非常小的斑块与周围区域类别不同的情况,这不符合实际情况,所以本文用其周围邻域的类别信息来对这些小块进行填充处理(图1e).图1f给出了获得的赤道向边界(红色外边界点)和极向边界(绿色内边界点)在原始图像上的叠加效果图.为了能更好地进行后续回归分析,本文对一些不好的分割结果进行了人工剔除,如一些“θ极光”.
2.3实验数据集构建
经过上述处理,本文共得到了极向边界分割很好的61210幅图像和赤道向边界分割很好的60180幅图像.为了研究不同参数对极光卵边界的影响,获得的边界点被进一步地处理(每一个边界点自带有UT时间、磁地方时、地磁纬度等信息;根据UT时间,可从OMNI数据库中查询到与其对应的行星际和地磁参数值).首先,本文仅仅关注位于北半球的边界点.其次,删除那些有一个或多个参数值为无效值的边界点.第三,对每个参数,包括地磁纬度,本文忽略那些不经常出现的情况,即那些参数值特别大或特别小的数据(在20个bin的直方图里,那些出现频率小于0.02的bin里的数据视为不经常出现的数据),因为这些点不是统计上显著的,仅仅在一些极端的地磁活动现象时出现.第四,本文认为5 min间隔内极光卵边界位置变化不会超过5地磁纬度.这样处理之后,~3805000个极向边界点和~1215000个赤道向边界点被提取出来.图2按磁地方时排列给出了这些点的综观分布图.第五,因为在后续的极光卵预测模型建立环节,是以一个磁地方时为单位建立一个预测模型,因此,本文将同一幅图像内(UT时间相同)、同一个磁地方时内的所有边界点进行了合并,地磁纬度用其均值表示.
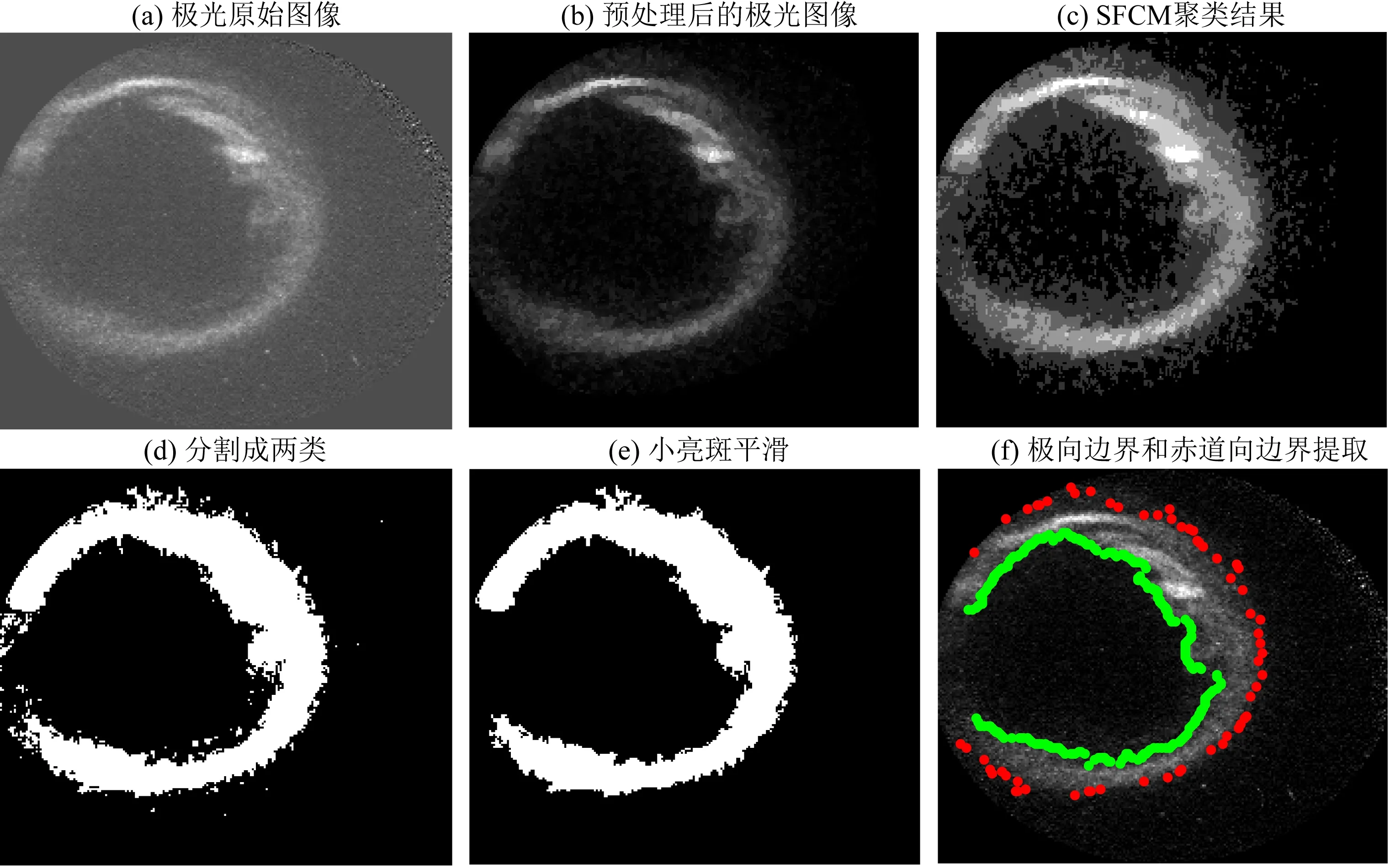
图1 极光卵边界抽取过程示意图(a) 极光原始图像; (b) 预处理后的极光图像; (c) 用SFCM算法聚类得到的结果; (d) 根据聚类结果把极光分割为2类(即极光卵区域和背景区域); (e) 对分割结果做进一步平滑处理; (f) 获得的极光卵极向边界(绿色内边界)和赤道向边界(红色外边界)在原始图像上的叠加图.Fig.1 Diagrams of the process of determining auroral oval boundaries(a) The original auroral image; (b) The image after pre-processing; (c) The result after SFCM clustering; (d) Two classes (auroral oval areas and background respectively) obtained from the segmenting results; (e) Filling the blocks by setting their classes the same with their neighbors; (f) The obtained equatorward boundary (red points) and poleward boundary (green points).
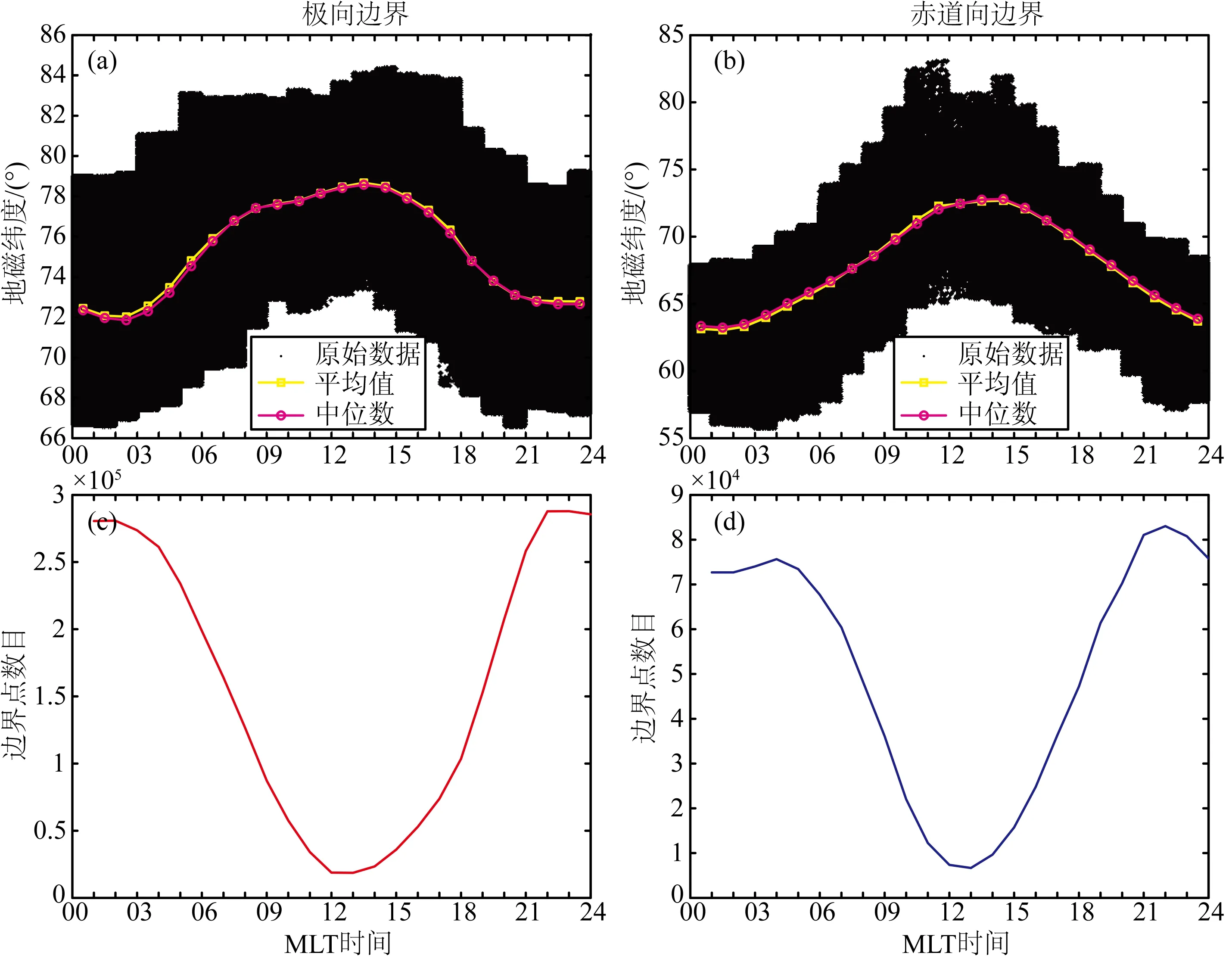
图2 子图(a)和(b)分别为极光卵极向边界点和赤道向边界点的散点图,其中黄色正方形和粉色圆圈分别表示每个小时内边界点地磁纬度的平均值和中位数值;子图(c)和(d)分别给出了极向和赤道向边界点的数目的综观分布Fig.2 The top two panels are the scatter diagrams of poleward boundary points (a) and equatorward boundary points (b). The yellow squares and pink circles represent the average and median magnetic latitude of boundary points in each one-hour bin, respectively. The bottom panel (c) and (d) shows the synoptic distribution of the point numbers of poleward and equatorward boundary, respectively
3数据分析及结果
太阳风、IMF、地磁参数等不同的空间参数之间存在一定的相关关系,这些互相关可能会影响对结果的分析.因此,在数据分析之前有必要对变量之间的互相关性进行讨论.表1给出了6个行星际参数以及地磁活动指数AE的相关系数矩阵,上三角矩阵表示极向边界数据,下三角表示赤道向边界数据.众所周知,太阳风动压(Pdyn)变化主要来自于太阳风密度(Np)的变化,在本文数据库里Pdyn和Np之间也显示出了很高的相关性,赤道向/极向数据的相关系数分别为r=0.874/0.860(在公式r=n1/n2中,n1表示赤道向边界的系数,n2表示极向边界的系数,以下同).行星际参数之间还存在两个中度负相关,即IMFBx和By之间相关系数为r=-0.468/-0.464,而太阳风速度(Vp)和密度(Np)之间相关关系为r=-0.633/-0.625.地面观测指数AE与行星际参量之间的相关系数都非常低(绝对值小于0.2).在后续的预测模型构建中,将Bx、By、Bz、Vp、Np、AE作为彼此独立的参量进行分析.
3.1单变量分析
为了描述太阳风等离子体和行星际磁场对极光卵边界的影响,在每个磁地方时处,极向/赤道向边界点分别根据这6个行星际参数和地磁指数AE、Sym-H进行了分段合并,划分成20个数据区间段.结果分别在图3a和3b中予以显示,其中纵轴表示每个区间段里所有数据点地磁纬度的均值.需要注意的是,因为划分数据区间段时,各区间段里的数据点数目是相同的,所以对每个参数而言各区间段的长度是不规则的.类似的分段划分方法在以往论文(Carbary, 2005; Liou et al., 2001; Shue et al., 2002)都有用到.
从图3a中我们可以看到行星际磁场、太阳风参数会导致极光卵边界呈现如下变化特征:
(1) 随着IMFBz分量的减小(尤其是Bz负值时),日侧极向边界 (0600—1800 MLT)和夜侧赤道向边界(1800—0600 MLT) 呈现一个显著的赤道向偏移.这是由于南向行星际磁场有利于日侧重联的发生,使得开放的磁通量大量进入极盖,从而导致极盖区面积增大,极盖边界向赤道向膨胀.
(2) 随着IMFBy分量的减小,晨昏和夜侧极光卵(1800—0600 MLT)的极向/赤道向边界呈现一个极向偏移.这种变化可能由与IMFBy有关的半球间场向电流导致(Kozlovsky et al., 2003, 2007; Østgaard and Laundal, 2012).
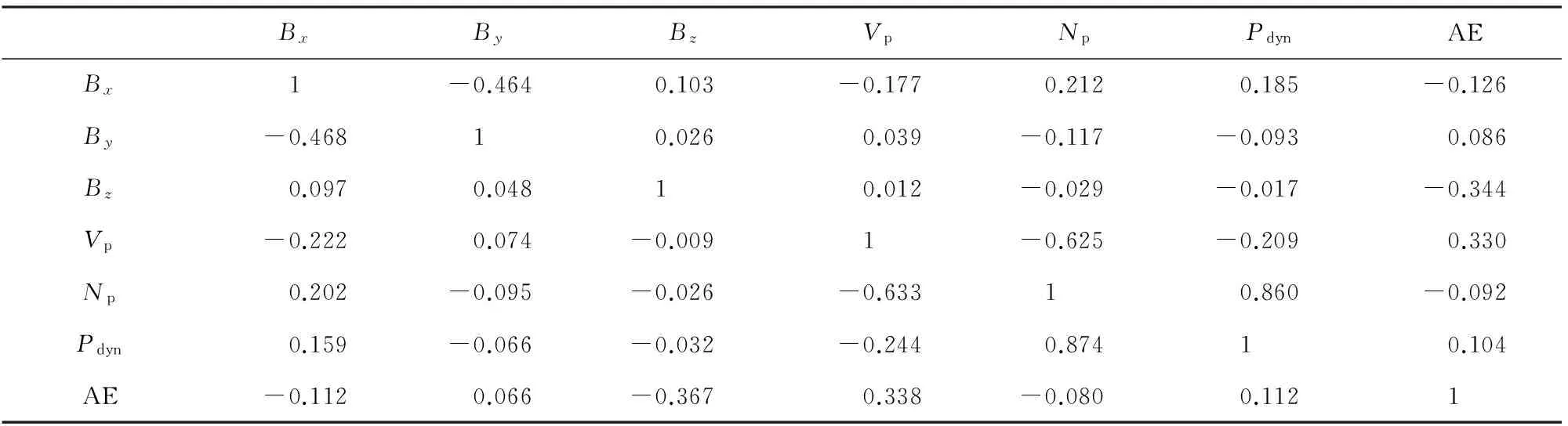
表1 极光卵极向边界点和赤道向边界点的相关系数矩阵.下三角表赤道向边界,上三角表极向边界
(3) 随着IMFBx分量的增大,日侧极光卵的极向边界向极向移动.因为电离层越极盖电势和磁层顶重联率是随IMFBx的增加而减小(Peng et al., 2010).减小的日侧磁重联率导致进入极盖区的开放磁通量的减少,从而使得极盖区面积收缩,极光卵极向边界向极向移动.
(4) 在夜侧扇区极光卵极向/赤道向边界随着太阳风动压的增大而近似线性地向赤道向移动.先前的观测和模拟显示太阳风动压的增加能增强电离层越极盖电势和相应的场向电流强度,这可以导致全球极光活动强度的增强,极光卵的纬度活动范围向低纬扩展(Peng et al., 2011).
(5) 夜侧极光卵2100—0300 MLT扇区的极向边界和1800—0300MLT的赤道向边界随着太阳风速度的增加而向低纬偏移;
(6) 0000—0900MLT扇区的赤道向边界随着太阳风密度的增加而向极向偏移.
不同的地磁活动指数适用于表征不同类型或动力学过程的地磁活动强弱.分析极光卵与地磁活动指数之间的变化关系,可以给出不同类型的地磁活动对极光卵的影响的物理信息.如图3b所示.
(1) 随AE指数的增大,极光卵极向/赤道向边界向赤道向扩展.AE指数常用于表征磁层亚暴活动的强弱,因此,可以认为极光卵随着磁层亚暴活动的增强,而向赤道向膨胀.
(2) 环电流指数Sym-H相对于其他空间环境变量,其与极光卵之间相互关系的线性特征表现最不明显.但这并不意味着Sym-H所表征的环电流对极光卵没有影响(Milan, 2009).
此外,由图3可知,1)在不同的磁地方时,任何一个参数与极光卵边界的相互关系是不同的.因此我们需要对每个磁地方时分别做回归分析.2)极光卵的活动是磁层和磁层边界层各类动力学过程的一个综合反映,没有哪个空间参数可以单独将其完全表征.所以,需要多元回归分析.3)8个空间参数中,规律性表现最不明显的是环电流密度Sym-H指数,因此本文两个多元回归模型没有考虑加入Sym-H作为回归量.
3.2多元回归分析
3.2.1回归方法及评价准则
回归分析是研究变量之间关系的一种统计工具(Sykes, 1993).多元回归模型能包含独立或交互作用的多个变量,共同解释因变量的变化.以上述空间参数为自变量的回归模型不仅能预测极光卵边界的预期位置,还能估计由于某个参数变化而导致的边界位置的变化量.
线性回归是回归分析中最简单、并在实际应用中得到了广泛使用的一种方法,因为线性依赖于未知参数的模型比非线性更容易拟合,产生的估计的统计特性也更容易确定.在本文的研究中,导致极光卵变化的具体原因尚不明确,无法给出回归模型的具体形式,所以为了简单起见,本文选用常用的线性回归分析方法.
在统计学中,确定性系数(R2),F统计量和t统计量常常用来对一个回归模型进行评估,但对海量的极光数据量而言,每个系数都很可能是统计有意义的.为了考察回归模型的实际效果(而非这些统计指标),本文中极光卵边界数据集被分成了两部分,一部分数据用来拟合回归模型的系数,另一部分数据当做测试集:根据测试集数据对应的行星际和地磁环境参数,用训练好的模型来对其极光卵边界位置进行预测.预测值与实际边界纬度之间的平均绝对误差(MAD)用来评估模型效果.
3.2.2回归建模
用一元线性回归模型,利用行星际和地磁参数,对赤道向和极向极光卵边界位置进行建模.因变量取赤道向或极向极光卵边界的地磁纬度值,自变量取行星际和地磁参数.每一个磁地方时处的极向/赤道向边界纬度都被拟合成了部分空间参数的线性函数,具体考虑如下2个模型:
(1) 模型1:旨在从源头来研究极光卵的变化.考虑行星际磁场(IMF)三分量和太阳风三分量对极光卵边界位置的影响,即模型参量包括6个行星际分量(IMFBx,By,Bz;Pdyn,Vp,Np).模型1的回归方程为
+a4·Pdyn+a5·Vp+a6·Np,
(2) 模型2:模型1没有考虑夜侧极光有关的动力学过程,所以在模型2中,本文加入了与夜侧极光活动紧密相关的地磁指数:极光电集流指数AE.同时,与模型1相比,去掉了与太阳风速度和动量密切相关的太阳风动压参量,即在模型2中,模型参量包括5个行星际独立参量 (IMFBx,By,Bz;Vp,Np) 以及地磁指数AE.模型2的回归方程为
+b4·Vp+b5·Np+b6·AE,
其中,b0—b6表示模型2的回归系数.
对上述2个模型来说,因为在不同的磁地方时(共24 h),每一个参数与极光卵边界的相互关系都是不同的,因此建模的时候按24个MLT分别做回归建模.
表2—5给出了回归模型1、2的极向边界和赤道向边界回归模型系数(由于OMNI数据中,Vp的单位用的百公里/秒,所以回归建模时Vp参数值除以100).根据这些模型系数,对任意给定的行星际和地磁条件,按照相应的回归模型即可计算出与之对应的极向和赤道向极光卵边界位置.
3.2.3预测结果评价
极光卵边界位置预测包含定性和定量两方面的评价.其中定量评价为:根据行星际和地磁参数用回归模型估计极光卵边界位置,计算其与真实边界的平均绝对误差值(MAD),给出各模型的效果.定性评价为:对比UVI图像极光卵的真实边界、SFCM聚类算法自动分割得到的边界以及运用回归模型得到的预测边界,视觉比较三种边界,评价自动分割的结果及模型预测的效果.
(1) 定量评价:为了评价模型的实际效果,本文把数据集分为4:1两部分,用80%的数据来拟合模型参数,剩余20%当做测试集;用训练好的模型根据测试集数据的行星际地磁参数来对其极光卵边界纬度进行估计预测.预测纬度与实际边界之间的平均绝对误差(MAD)用来评价模型好坏.这个过程在整个极光卵数据库上重复操作五次,每次都用不同的20%数据作为测试集.这就是所谓的五重交叉验证(five-fold cross-validation)方法.为了使结果可靠,本文进行了5轮上述操作,每一轮的数据划分都不一样.这样得到的25个MAD值取平均后即为最终结果(图4).MAD值越小越好.可以看出,回归模型2的效果比模型1好,这也符合我们之前的分析:因为模型1没有加入表征夜侧极光活动的参量.极向边界最佳预测出现在15MLT处,误差为1.23MLAT,平均误差为1.55MLAT,而对赤道向边界,最佳预测出现在20MLT处,为1.21MLAT,平均误差为1.66MLAT.
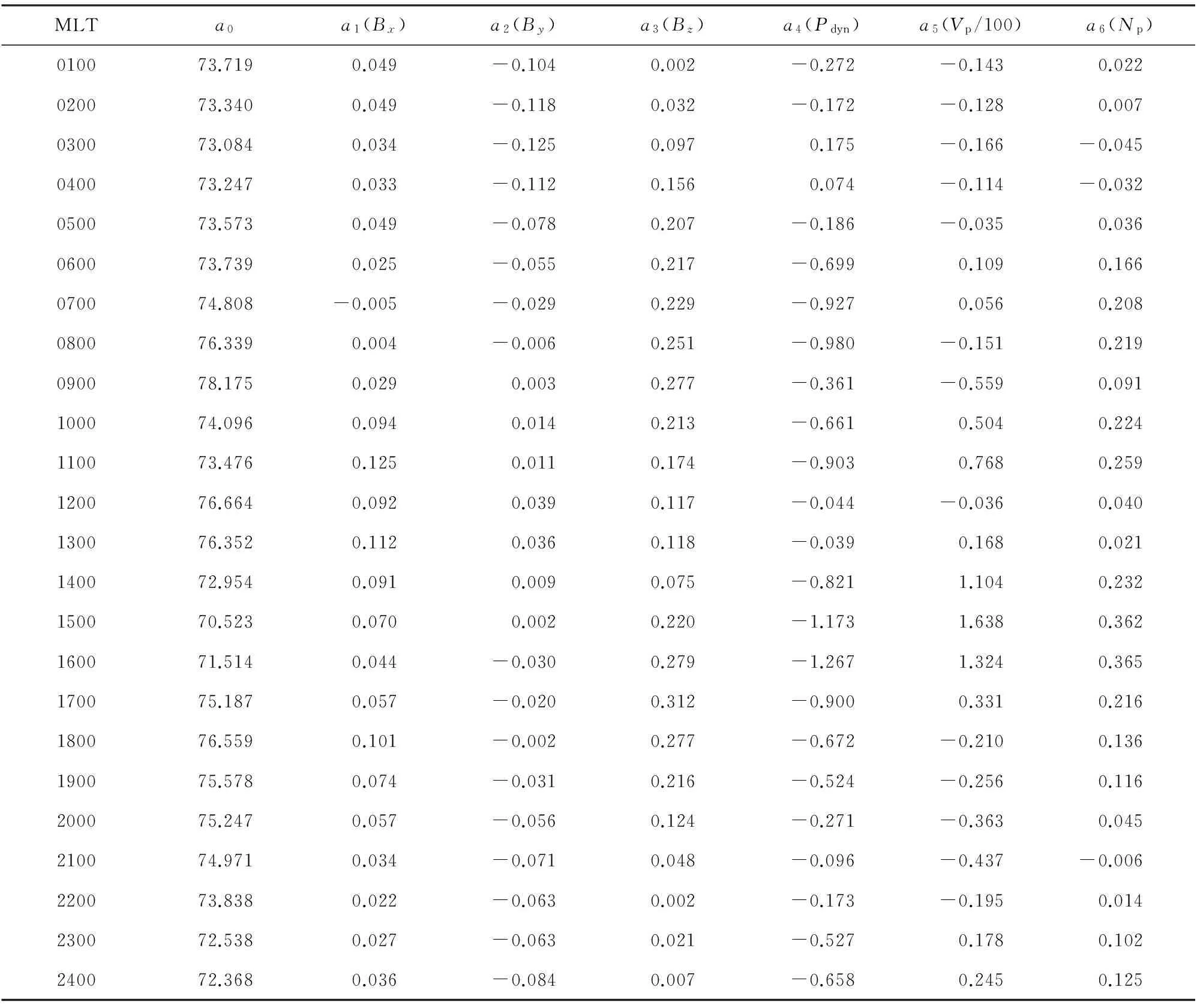
表2 0100—2400MLT时刻回归模型1的极向边界回归模型系数

表3 0100—2400MLT时刻回归模型1的赤道向边界回归模型系数
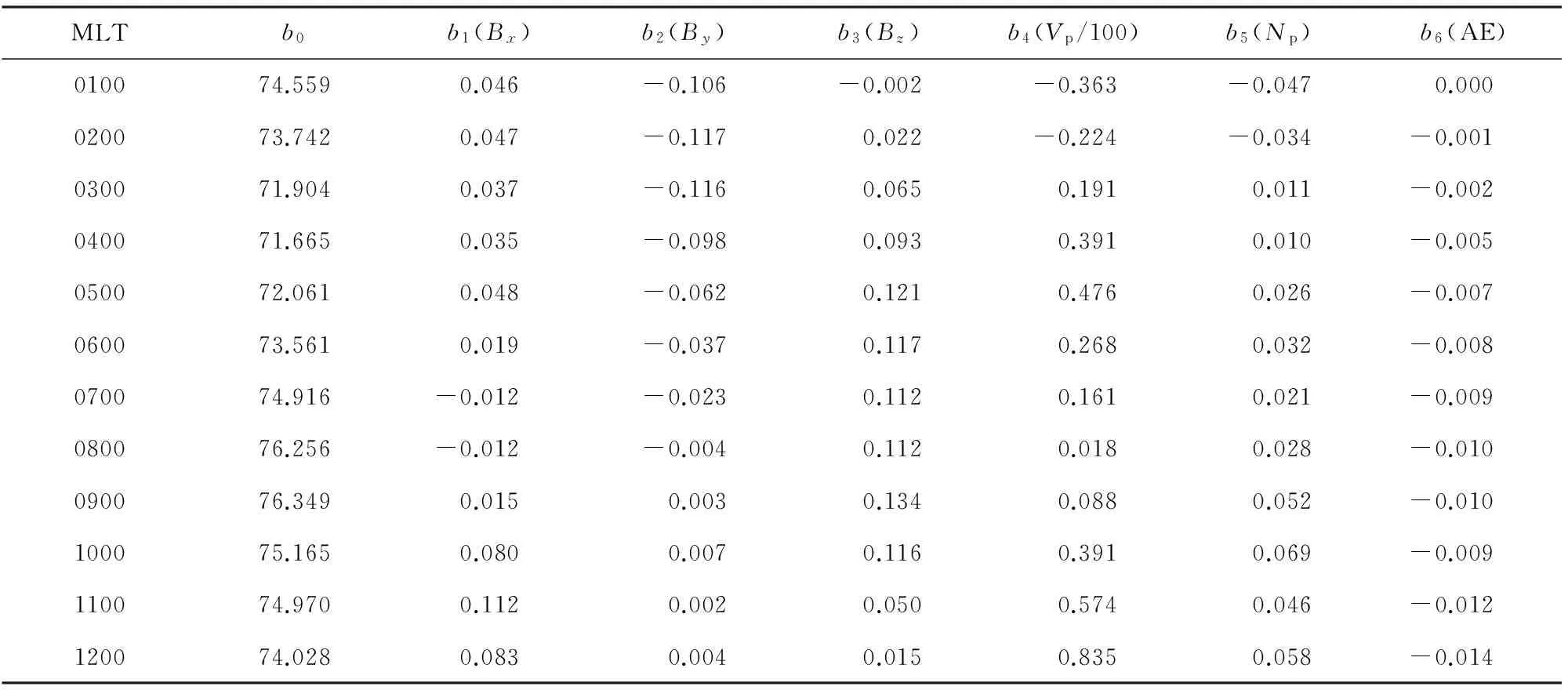
表4 0100—2400MLT时刻回归模型2的极向边界回归模型系数
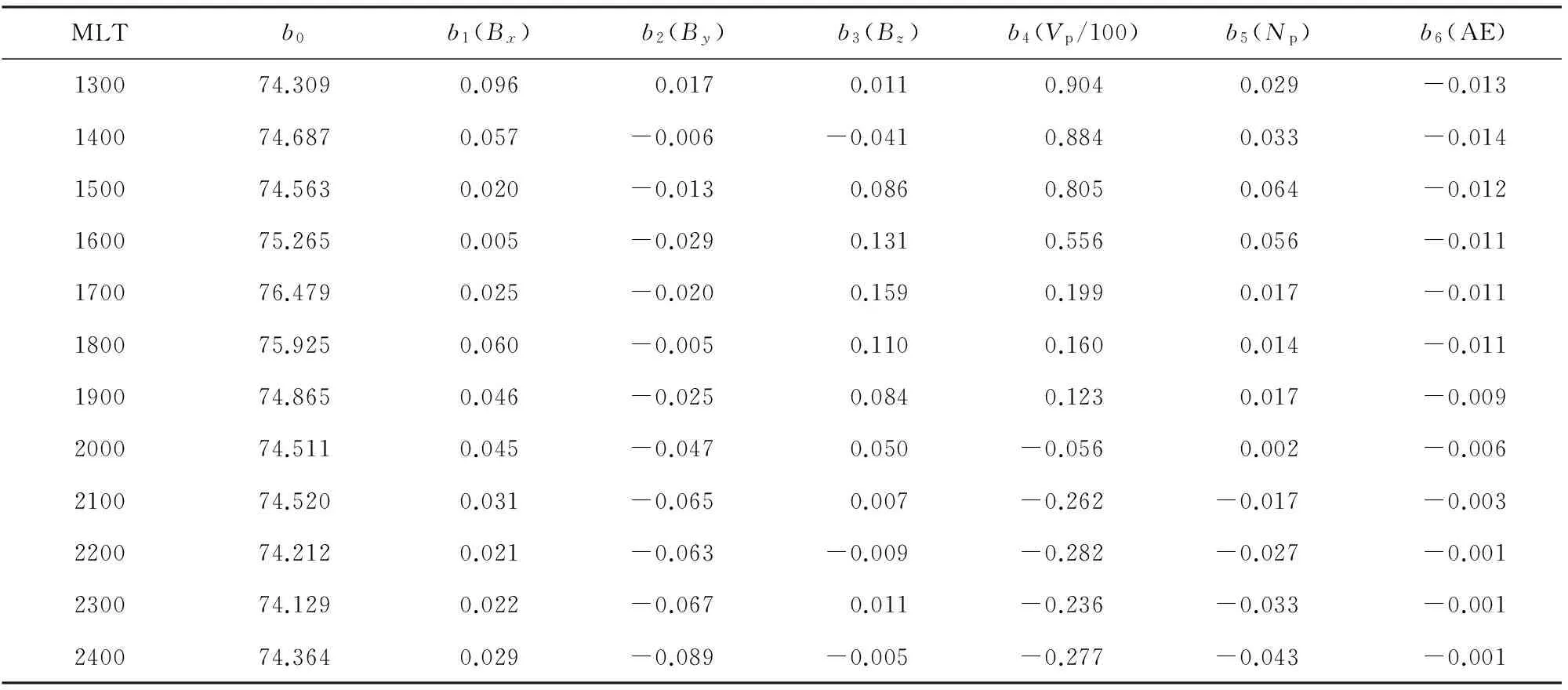
续表4
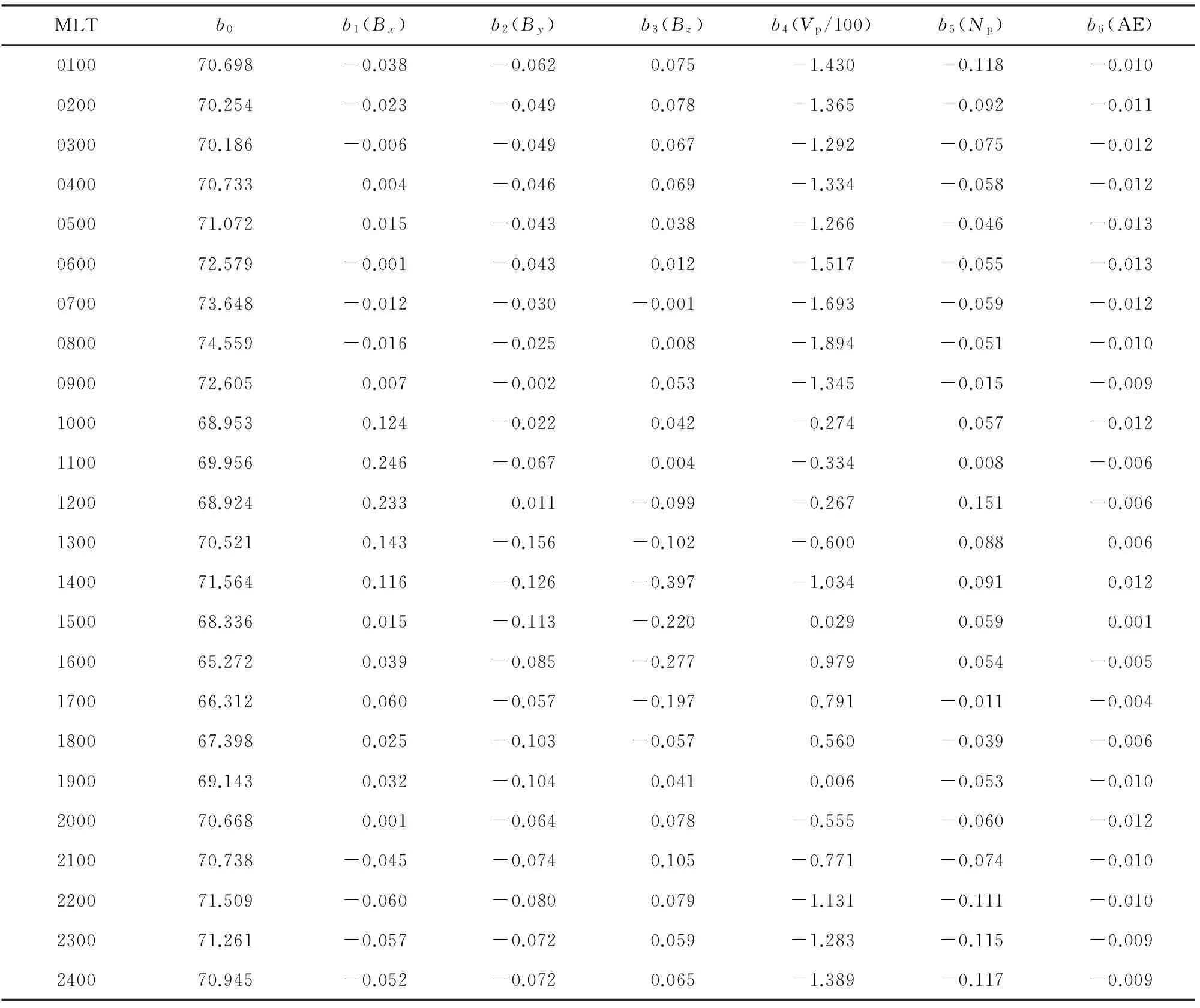
表5 0100—2400MLT时刻回归模型2的赤道向边界回归模型系数
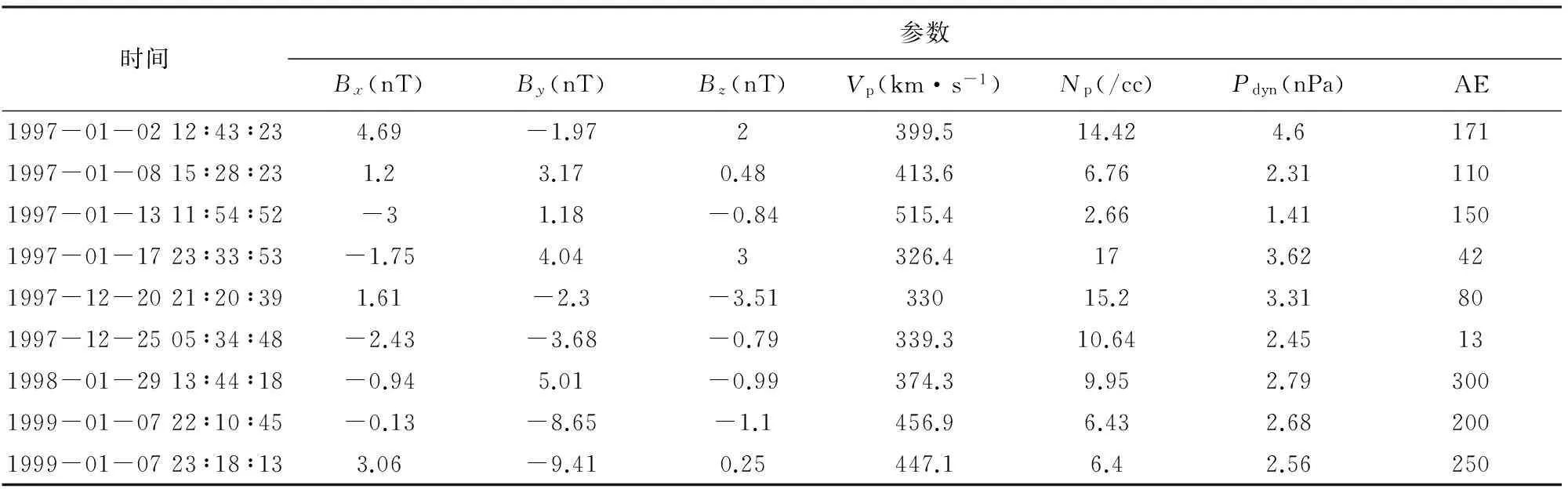
(2) 定性评价:除了上述定量评价之外,图5给出了极坐标系下9幅UVI图像,我们可以从视觉上比较极光卵的真实边界(白色阴影区域)、SFCM自动分割得到的边界(蓝色点)及运用回归模型2得到的预测边界(绿色点),对比三种边界之间的差异,由此定性评价本文的方法效果.

图4 本文2个模型预测结果与极光卵实际边界的平均绝对误差图,其中五角星实线表极向边界预测误差, 圆圈虚线表赤道向边界预测误差Fig.4 The mean values of MAD of the two models proposed in this paper, where the five-pointed star full line represents the MAD of the poleward boundary, and the circle dashed line gives the MAD of the equatorward boundary
极向回归模型和赤道向回归模型中的系数详见表4和表5.
3.3与现有模型对比
为了将本文模型和已有文献中极光卵模型进行比较,本文选取了比较有代表性的Kp模型(Carbary, 2005)和复合模型(Milan, 2009)两个模型与本文模型2进行比较.其中Carbary的Kp模型极向和赤道向回归方程分别为
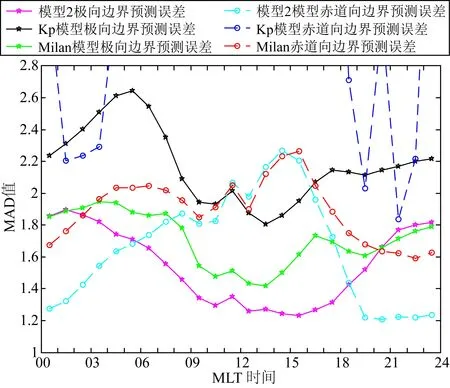
图6 本文模型2与Carbary的Kp模型和Milan模型对比.其中五角星实线表极向边界预测误差,圆圈虚线表赤道向边界预测误差Fig.6 The comparisons between model 2 proposed in this paper and Carbary′s and Milan′s models, where the five-pointed star full line represents the MAD of the poleward boundary, and the circle dashed line gives the MAD of the equatorward boundary
时间参数Bx(nT)By(nT)Bz(nT)Vp(km·s-1)Np(/cc)Pdyn(nPa)AE1997-01-0212∶43∶234.69-1.972399.514.424.61711997-01-0815∶28∶231.23.170.48413.66.762.311101997-01-1311∶54∶52-31.18-0.84515.42.661.411501997-01-1723∶33∶53-1.754.043326.4173.62421997-12-2021∶20∶391.61-2.3-3.5133015.23.31801997-12-2505∶34∶48-2.43-3.68-0.79339.310.642.45131998-01-2913∶44∶18-0.945.01-0.99374.39.952.793001999-01-0722∶10∶45-0.13-8.65-1.1456.96.432.682001999-01-0723∶18∶133.06-9.410.25447.16.42.56250
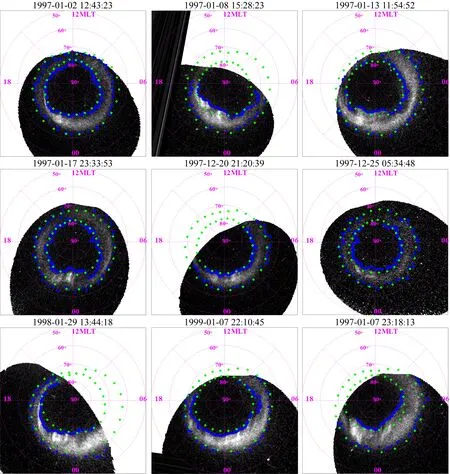
图5 UVI图像极光卵的真实边界,SFCM自动分割得到的边界(蓝色点)和运用回归模型2得到的预测边界(绿色点)对比Fig.5 Comparison of the original UV observation, the auroral boundaries calculated by the SFCM automatic segmentation method (shown as the small blue dot) and the regression model 2 (illustrated as the green dot)
其中c0和c1为回归系数,上标PO和EQ分别表示极向边界和赤道向边界.Milan的复合模型综合考虑了行星际条件和地球环电流对极光卵的影响.其中环电流密度用Sym-H指数HSYM表征,而行星际条件用日侧重联率ΦD表征.ΦD用ACE卫星观测到的上行太阳风条件来计算:
即Kan-Lee重联电场乘以一个特征长度尺度以匹配日侧重联率的观测.其中RE是地球半径(6371 km),VSW是太阳风速度,By和Bz是IMF的两个分量,θ是IMF时钟角.这样表示以后,Milan认为极光卵半径长度即可用HSYM和ΦD来线性表示:
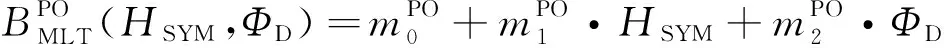
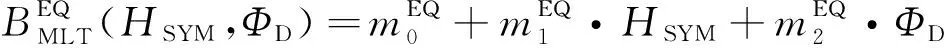
其中m0和m1为回归系数,上标PO和EQ分别表示极向边界和赤道向边界.
与本文模型2的建立过程一样,Carbary的Kp模型和Milan的复合模型在回归建模时,无论是赤道向边界还是极向边界,本文也都是对每个磁地方时分别进行回归分析;同样也是把数据集分成4∶1两部分,进行25次实验,计算平均绝对误差MAD.图6给出了本文模型2与Kp模型及Milan模型的模型预测误差结果.从图中我们可以看出,本文模型除了赤道向边界的预测结果在正午及午后四个小时稍微落后于Milan模型,其他时间的表现都远远超过Kp模型和Milan模型.表现最差的是Kp模型,尤其是其对日侧赤道向极光卵边界的预测,误差范围超出了图6的图示范围.
4问题讨论
(1) 回归分析时最大的困难在于影响极光卵变化的物理过程尚不明确,因而无法准确给出回归模型的具体形式.多元线性回归模型虽然简单,但回归模型的R2值偏小,说明可能还有一些其他的空间参数或更复杂的参数组合形式(如幂指数、三角函数形式、除法等)需要被考虑.如果回归方程的形式确定了,基于海量数据集用回归分析方法就能很容易地求出比较可靠的回归系数.
(2) 回归分析的边界数据来自于极光卵边界的自动提取,而SFCM分割算法存在误差.为了得到更精确的回归模型,分割方法还有待进一步改进.
(3) OMNI数据是在磁层顶给出的,需要考虑在电离层看到极光现象时经历的延迟时间.本文使用的是经典的7 min时延(穿越磁鞘5 min时延+到达电离层2 min Alfven分波传送时间),可实际情况是日侧和夜侧的传播时间是不同的.在将来的工作中,我们需要对此进行详细的讨论.
(4) 本文只使用了冬季极光卵数据,没有考虑季节变化对极光卵所带来的影响.为了得到更普适的极光卵模型,在将来的工作中,还需要加入其他季节的数据.
5结论
本文充分利用了Polar卫星返回的海量UVI图像数据来研究不同空间环境对极光卵边界位置的影响.SFCM聚类方法被用来自动分割极光卵边界,为回归分析提供了海量边界点数据.大数据库本身可以作为一个查询表,用于对给定的空间环境定位极光卵的位置.作为研究极光卵随行星际和地磁环境变化的一项初步研究,本文最大的问题在于具体的物理模型是未知的.本文仅采用简单的一次多项式来构建回归模型,多次五重交叉验证实验保证了结果的可靠性.极光卵边界的实际地磁纬度和模型预测值之间的MAD值被用来定量评价回归模型的效果.对极向边界而言,平均MAD值~1.55个地磁纬度,对赤道向边界来说,平均MAD值~1.66个地磁纬度;通过与以往论文中2个经典模型预测结果定量比较,以及举例对比极光卵真实边界和预测结果,证明本文提出的方法是有效的.本文对每个磁地方时处的极光卵极向、赤道向边界位置进行了多元回归建模,这样得到的回归模型可以用来对所有磁地方时处的极光卵极向、赤道向边界的地磁纬度进行预测,因而可以用于空间天气中预测整个极光卵的位置.
References
Brittnacher M, Fillingim M, Parks G, et al. 1999. Polar cap area and boundary motion during substorms.J.Geophys.Res., 104(A6): 12251-12262.
Carbary J F. 2005. A Kp-based model of auroral boundaries.SpaceWeather, 3(10): S10001.
Cho J S, Lee D Y, Kim K C, et al. 2010. Response of the poleward boundary of the nightside auroral oval to impacts of solar wind dynamic pressure enhancement.J.Astron.SpaceSci., 27(3): 189-194.
Chuang K S, Tzeng H L, Chen S, et al. 2006. Fuzzy c-means clustering with spatial information for image segmentation.ComputerizedMedicalImagingandGraphics, 30(1): 9-15.
Cowley S W H, Morelli J P, Lockwood M. 1991. Dependence of convective flows and particle precipitation in the high-latitude dayside ionosphere on theXandYcomponents of the interplanetary magnetic field.J.Geophys.Res., 96(A4): 5557-5564. Hardy D A, Burke W J, Gussenhoven M S, et al. 1981. DMSP/F2 electron observations of equatorward auroral boundaries and their relationship to the solar wind velocity and the north-south component of the interplanetary magnetic field.J.Geophys.Res., 86(A12): 9961-9974.
Holzworth R H, Meng C I. 1975. Mathematical representation of the auroral oval.Geophys.Res.Lett., 2(9): 377-380.
Holzworth R H, Meng C I. 1984. Auroral boundary variations and the interplanetary magnetic field.Planet.SpaceSci., 32(1): 25-29.
Hu Z J, Yang H G, Huang D, et al. 2009. Synoptic distribution of dayside aurora: Multiple-wavelength all-sky observation at Yellow River Station in Ny-Ålesund, Svalbard.J.Atmos.Sol.-Terr.Phys., 71(8-9): 794-804.
Hu Z J, Yang H G, Liang J, et al. 2010. The 4-emission-core structure of dayside aurora oval observed by all-sky imager at 557.7 nm in Ny-Ålesund, Svalbard.J.Atmos.Sol.-Terr.Phys., 72(7-8): 638-642. Hu Z J, Yang H G, Han D S, et al. 2012. Dayside auroral emissions controlled by IMF: A survey for dayside auroral excitation at 557.7 and 630.0 nm in Ny-Ålesund, Svalbard.J.Geophys.Res., 117: A02201.
Hu Z J, Yang H G, Hu H Q, et al. 2013. The hemispheric conjugate observation of postnoon “bright spots”/auroral spirals.J.Geophys.Res.SpacePhys., 118(4): 1428-1434. Hu Z J, Ebihara Y, Yang H G, et al. 2014. Hemispheric asymmetry of the structure of dayside auroral oval.Geophys.Res.Lett., 41(24): 8696-8703.Huang C S, DeJong A D, Cai X. 2009. Magnetic flux in the magnetotail and polar cap during sawteeth, isolated substorms, and steady magnetospheric convection events.J.Geophys.Res., 114(A7): A07202.
Kauristie K. 1995. Statistical fits for auroral oval boundaries during the substorm sequence.J.Geophys.Res., 100(A11): 21885-21895.
Kozlovsky A, Turunen T, Koustov A, et al. 2003. IMFByeffects in the magnetospheric convection on closed magnetic field lines.Geophys.Res.Lett., 30(24), doi: 10.1029/2003GL018457.
Kozlovsky A, Meurant M, Turunen T. 2007. Changes of dayside auroral distribution caused by a solar wind pressure pulse and associated interplanetary magnetic field disturbances.Ann.Geophys., 25(4): 929-940.
Lee D Y, Lyons L R, Yumoto K. 2004. Sawtooth oscillations directly driven by solar wind dynamic pressure enhancements.J.Geophys.Res., 109(A4): A04202.
Liou K, Newell P T, Meng C I, et al. 1998. Characteristics of the solar wind controlled auroral emissions.J.Geophys.Res., 103(A8): 17543-17557.
Liou K, Newell P T, Sibeck D G, et al. 2001. Observation of IMF and seasonal effects in the location of auroral substorm onset.J.Geophys.Res., 106(A4): 5799-5810.
Lyons L R. 2000. Geomagnetic disturbances: Characteristics of distinction between types, and relations to interplanetary conditions.J.Atmos.Sol.-Terr.Phys., 62(12): 1087-1114.Meng C I. 1980. Polar cap variations and the interplanetary magnetic field.∥ Dynamics of the Magnetosphere. Netherlands: Springer, 23-46.
Milan S E. 2009. Both solar wind-magnetosphere coupling and ring current intensity control of the size of the auroral oval.Geophys.Res.Lett., 36(18): L18101.
Milan S E, Hutchinson J, Boakes P D, et al. 2009. Influences on the radius of the auroral oval.Ann.Geophys., 27(7): 2913-2924. Milan S E, Evans T A, Hubert B. 2010. Average auroral configuration parameterized by geomagnetic activity and solar wind conditions.Ann.Geophys., 28(4): 1003-1012.Østgaard N, Laundal K M. 2012. Auroral asymmetries in the conjugate hemispheres and interhemispheric currents.∥ Auroral Phenomenology and Magnetospheric Processes: Earth and Other Planets. Washington, D. C.: American Geophysical Union, 99-111, doi: 10.1029/2011GM001190.
Peng Z, Wang C, Hu Y Q. 2010. Role of IMFBxin the solar wind-
magnetosphere-ionosphere coupling.J.Geophys.Res., 115(A8): A08224, doi: 10.1029/2010JA015454. Peng Z, Wang C, Hu Y Q, et al. 2011. Simulations of observed auroral brightening caused by solar wind dynamic pressure enhancements under different interplanetary magnetic field conditions.J.Geophys.Res., 116(A6): A06217, doi: 10.1029/2010JA016318.
Shue J H, Newell P T, Liou K, et al. 2002. Solar wind density and velocity control of auroral brightness under normal interplanetary magnetic field conditions.J.Geophys.Res., 107(A12): SMP 9-1-SMP 9-6.Sigernes F, Dyrland M, Brekke P, et al. 2011a. Real time aurora oval forecasting-SvalTrackII.Opt.PuraApl., 44(4): 599-603. Sigernes F, Dyrland M, Brekke P, et al. 2011b. Two methods to forecast auroral displays.J.SpaceWeatherSpaceClim., 1(1): A03. Starkov G V. 1969. Analiticheskoe predstavlenie ekvatorial′noy granitsy oval′noy zony polyarnikh siyaniy (Analytical representation of the equatorward boundary of the polar auroral oval).GeomagnAeron, 9(759).Starkov G V. 1994. Mathematical model of the auroral boundaries.GeomagnetismandAeronomy, 34(3): 331-336. Sykes A O. 1993. An Introduction to Regression Analysis. Chicago: University of Chicago. Wang Q, Meng Q H, Hu Z J, et al. 2011. A method for extracting Auroral ovals in UVI images and its evaluation.ChineseJournalofPolarResearch(in Chinese), 23(3): 168-177.
Yang Q J, Liang J M, Liu J M, et al. 2013. A method for automatic identification of substorm expansion phase onset from UVI images.ChineseJournalofGeophysics(in Chinese), 56(5): 1435-1447, doi: 10.6038/cjg20130502.Yang Y F, Lu J Y, Wang J S, et al. 2013. Influence of interplanetary magnetic field and solar wind on auroral brightness in different regions.J.Geophys.Res., 118(1): 209-217.Zhang Y, Paxton L J. 2008. An empirical Kp-dependent global auroral model based on TIMED/GUVI FUV data.J.Atmos.Sol.-Terr.Phys., 70(7-8): 1231-1242.
附中文参考文献
王倩, 孟庆虎, 胡泽骏等. 2011. 紫外极光图像极光卵提取方法及其评估. 极地研究, 23(3): 168-177.
杨秋菊, 梁继民, 刘俊明等. 2013. 一种基于紫外极光图像的亚暴膨胀期起始时刻的自动检测方法. 地球物理学报, 56(5): 1435-1447, doi: 10.6038/cjg20130502.
(本文编辑胡素芳)
基金项目国家自然科学基金(41504122,41274164,41431072,41374161, 61501285),中央高校基本科研业务费专项基金(GK201503020),国家海洋局极地科学重点实验室开放研究基金(KP201302),南北极环境综合考查与评估专项(CHINARE2016-02-03,CHINARE2016-04-01),浦东新区科技发展基金(Pkj2013-z01),中国科学院科学战略性先导科技专项(XDA04060201)资助.
作者简介杨秋菊,女, 1986年生,讲师,主要从事极光图像自动分析等方面的研究.E-mail: yangqiuju@snnu.edu.cn *通讯作者胡泽骏,男,1978年生,副研究员,主要从事极区电离层、极光以及磁层-电离层耦合方面的研究.E-mail:huzejun@pric.org.cn
doi:10.6038/cjg20160203 中图分类号P352
收稿日期2015-08-18,2015-11-29收修定稿
Modeling and prediction of ultraviolet auroral oval boundaries based on IMF/solar wind and geomagnetic parameters
YANG Qiu-Ju1, HU Ze-Jun2*, HAN De-Sheng2, HU Hong-Qiao2, MA Xiao1
1SchoolofPhysicsandInformationTechnology,ShaanxiNormalUniversity,Xi′an710119,China2SOAKeyLaboratoryforPolarScience,PolarResearchInstituteofChina,Shanghai200136,China
AbstractThe size of the auroral oval is closely related with the solar wind-magnetosphere-ionosphere coupling process, the accurate prediction of which plays an important role in space weather study and forecast. In this manuscript, a total of 3805000 poleward boundary points and 1215000 equatorward boundary points are automatically identified from Polar ultraviolet images by using the fuzzy c-means clustering method. With the massive dataset, we statistically analyze the relationship between the auroral oval boundaries and interplanetary magnetic field (IMF), solar wind parameters (SWP), and geomagnetic index. We construct two auroral boundary models by multivariate regression technique, which respectively used the IMF and SWP (model 1) and IMF, SWP and geomagnetic index (model 2) as the model parameters. With the Mean Absolute Deviation (MAD) of the auroral boundaries between the model predictions and the observations being an evaluator, the proposed model is further compared with the models proposed by Carbary (2005) and Milan (2009). The experimental results show that the MADs of model 2 are 1.55 MLAT and 1.66 MLAT for poleward boundary and equatorward boundary respectively, which are superior to the boundary models of Carbary (2005) (MADs are 2.18 and 5.47 MLAT) and Milan (2009) (MADs are 1.71 and 1.90 MLAT).
KeywordsUltraviolet aurora; Auroral oval boundary; Interplanetary and geomagnetic environments; Regression analysis
杨秋菊, 胡泽骏, 韩德胜等. 2016. 基于行星际/太阳风和地磁条件的紫外极光卵边界建模和预测.地球物理学报,59(2):426-439,doi:10.6038/cjg20160203.
Yang Q J, Hu Z J, Han D S, et al. 2016. Modeling and prediction of ultraviolet auroral oval boundaries based on IMF/solar wind and geomagnetic parameters.ChineseJ.Geophys. (in Chinese),59(2):426-439,doi:10.6038/cjg20160203.
