磁偶极子梯度张量的几何不变量及其应用

尹刚， 张英堂， 李志宁， 张光， 范红波

军械工程学院七系， 石家庄　050003



磁偶极子梯度张量的几何不变量及其应用

尹刚， 张英堂*， 李志宁， 张光， 范红波

军械工程学院七系， 石家庄050003

摘要磁梯度张量系统姿态的变化将影响梯度场测量和数据解释的精度，使得具有坐标变换不变性特点的张量不变量成为磁梯度张量数据解释的研究热点.本文在对磁偶极子产生的磁梯度张量进行特征值分析的基础上得到了：测量点与磁偶极子位置形成的位置矢量、磁偶极子磁矩矢量与绝对值最小的特征值对应的特征向量垂直；位置矢量和磁矩矢量与最大及最小特征值对应的特征向量共面，且两矢量间的夹角可由磁梯度张量矩阵的特征值表示.最后，将本文所得磁偶极子梯度张量的几何不变量用于磁性目标的跟踪中，取得了较好的实时跟踪效果.

关键词磁偶极子； 磁梯度张量； 几何不变量； 特征值； 张量不变量

1引言

磁梯度张量测量及解释应用被视为磁法勘探工作的一次突破(张昌达，2006； 2007)，其在资源勘探、军事、环境等领域都有着重要的应用价值(Schmidt and Clark，2000； 2006).磁梯度张量系统测量的对象是磁场矢量的梯度场，测量的结果受磁化方向影响小，能够反映目标体的矢量磁矩信息，且能更好地反演场源参数(方位、磁矩等)并对场源进行定位和追踪(张凤旭等，2007)，提高了磁源体的分辨率(马国庆等，2012).

磁梯度张量具有良好的数学性质，但其搭载在运动载体上使用时，载体姿态的变化将影响其测量和数据解释的精度(张光等，2013a)，由张量元素计算得到的张量不变量因其不受姿态变化的影响而得到了较多的关注，被广泛应用于磁性目标的定位及磁异常源的边界识别等多种场合(张光等，2013b).当探测距离大于2.5倍磁性物体长度时，可将磁性目标简化为磁偶极子模型(张朝阳等，2010)，因此，本文在张量不变量的基础上，以磁偶极子产生的磁梯度张量为对象，研究磁梯度张量矩阵、磁偶极子位置及磁矩间的本质关系，推导出了蕴含在其中的、不受姿态变化影响的固定几何关系，本文称之为磁梯度张量的几何不变量.

2磁梯度张量测量理论及张量不变量

磁梯度张量是磁场矢量的3个分量在相互正交的3个方向的空间变化率.若B为磁场矢量场，则磁梯度张量可以表示为两个三元素矢量的矩阵乘法运算：

(1)

其中,U为磁标势，Bx，By和Bz是磁场矢量B在空间相互正交的三个方向上的分量.

磁法勘探中地磁场及铁磁物质产生的异常场可看作无源的静磁场，因此，磁感应强度的散度和旋度为0，即：

(2)

由式(1)和(2)可知，磁梯度张量矩阵G为对称矩阵，其中9个元素中，只有5个是独立的，即只需得到其中的5个元素就可测得磁梯度张量.在磁法探测中，磁性目标简化为磁偶极子模型时可由6个未知量描述，即磁性目标的三维位置和三维磁矩.因此，磁矩矢量为m=(mx,my,mz)的磁偶极子，在距离其r=(x,y,z)处产生的磁矢量场(卞光浪等，2011)及磁梯度张量矩阵中的5个独立分量(Rimetal.，2012)可分别由下式计算得到

(3)

(4)

易知，磁梯度张量矩阵的特征值与坐标的选择无关，为张量的基本不变量(余天庆和毛为民，2006)，且张量矩阵的其余不变量可由特征值表示.设矩阵G的3个特征值为λ1，λ2和λ3，则由G的特征方程可得磁梯度张量的另外4个不变量，分别表示为

(5)

3几何不变量的证明

3.1磁梯度张量矩阵的特征值分析

(6)

将式(4)及式(5)代入式(6)可得磁偶极子产生的磁梯度张量矩阵的特征值：

(7)

令：δ=ec2+bcd+abc+d2e+ade+e3，ε=a2c+adc+abe+c3+ce2+bde，φ=bc2+cde-be2-ace，则磁偶极子产生的梯度张量的三个特征值对应的特征向量V1，V2，V3分别为

(8)

(9)

(10)

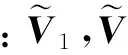
3.2几何不变量1

由式(7)中磁偶极子张量矩阵的特征值公式可知，假设3个特征值已由磁梯度张量系统测得的实际信号求解得到，则磁偶极子位置矢量与磁矩矢量间的夹角可由下式求解得到

(11)

由式(11)可知，磁梯度张量的特征值为张量不变量，因此，在磁梯度张量系统发生姿态变化时，由该公式计算得到的磁偶极子位置矢量与磁矩矢量间的夹角保持不变.本文将其定义为磁梯度张量的几何不变量1，其几何示意如图1所示.

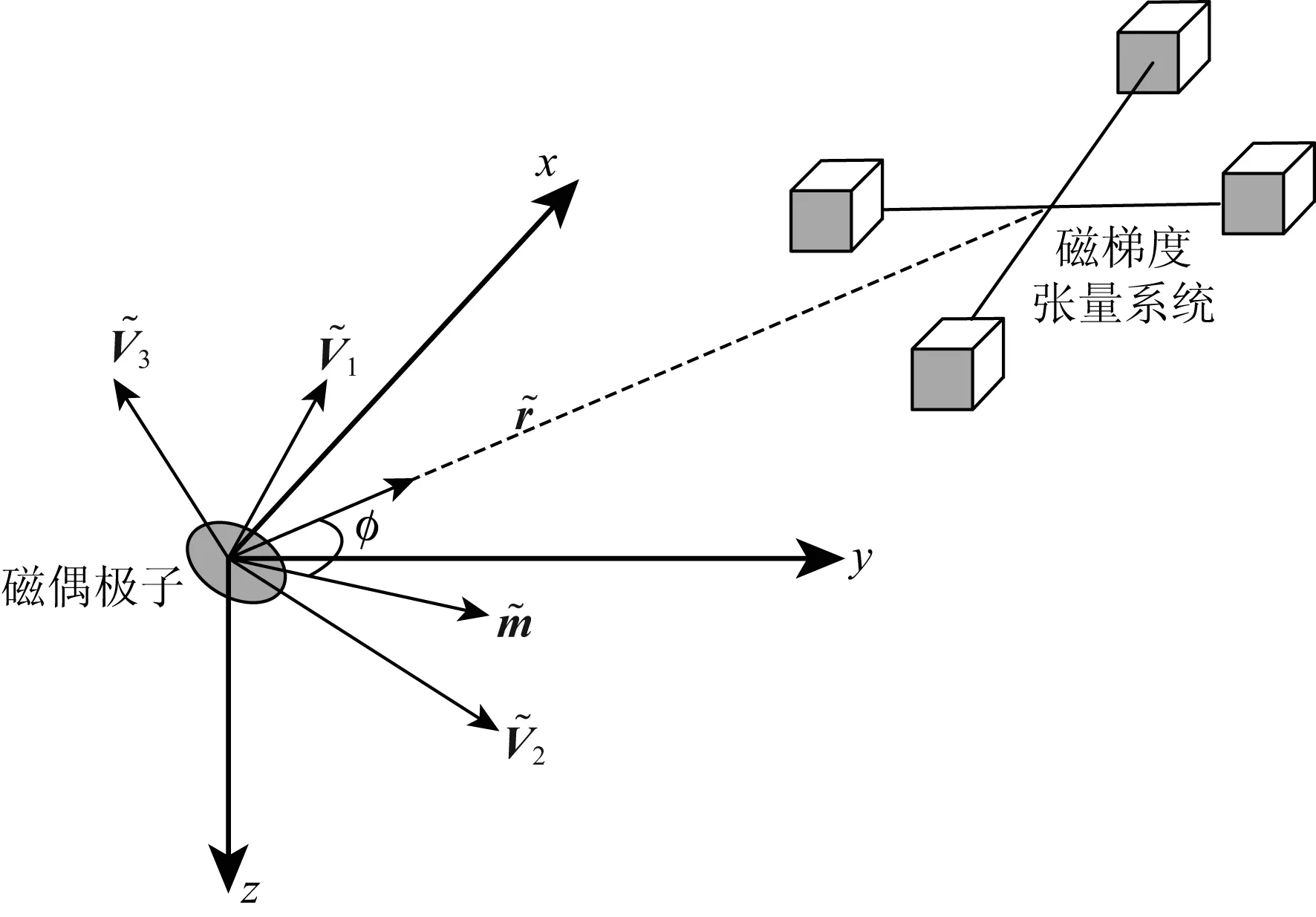
图1　磁偶极子梯度张量场的几何不变量示意图Fig.1　Sketch map of magnetic gradient tensor′s geometric invariants

由磁偶极子产生的磁矢量、磁梯度张量场公式及几何不变量1可得：

(12)

因此，基于本文推导的几何不变量1，若已知磁偶极子产生的总磁场强度及磁梯度张量信息，可通过特征值分析及公式(12)求得磁偶极子相对于测量点的距离R和磁矩模M.

3.3几何不变量2

将式(4)代入式(10)化简可得如下等式：

(13)

由式(13)可知，磁梯度张量矩阵G的绝对值最小的特征值对应的特征向量垂直于磁矩矢量和位置矢量，且不随着张量系统姿态的变化而变化.本文将此固定的垂直关系定义为磁梯度张量的几何不变量2.3.4几何不变量3

由对称矩阵的特征向量之间的几何关系可知，特征向量V3垂直于V1和V2；由几何不变量2可知，特征向量V3垂直于磁矩矢量m和位置矢量r，因此，假设向量V1，V2，m和r共面，则4个向量之间可互相表示，令

(14)

(15)

又磁偶极子产生的梯度张量场与矢量场满足欧拉反褶积公式(Reidetal.，1990；Naraetal.，2006；NaraandIto，2014)，且构造指数为3，即

(16)

(17)

则由式(14)及式(17)可得：

(18)

故磁偶极子位置矢量的单位向量可表示为

(19)

将式(15)及式(19)代入式(11)表示的几何不变量1，可求得式(15)中的等式系数：

(20)

由式(18)及式(20)可知，位置矢量及磁矩矢量与最大及最小特征值对应的特征向量共面，且不随着系统的姿态变化而变化，本文将其定义为几何不变量3.因此，几何不变量3可用于磁性目标的定位和磁矩反演.

在已知磁偶极子产生的磁梯度张量矩阵的情况下，可通过特征值分析，利用式(12)求解磁偶极子相对于测量点的距离和磁矩模，然后利用式(18)及式(20)求解磁偶极子的位置及磁矩矢量的单位向量，最终实现磁偶极子位置及磁矩矢量的正确反演，其几何示意如图2所示.

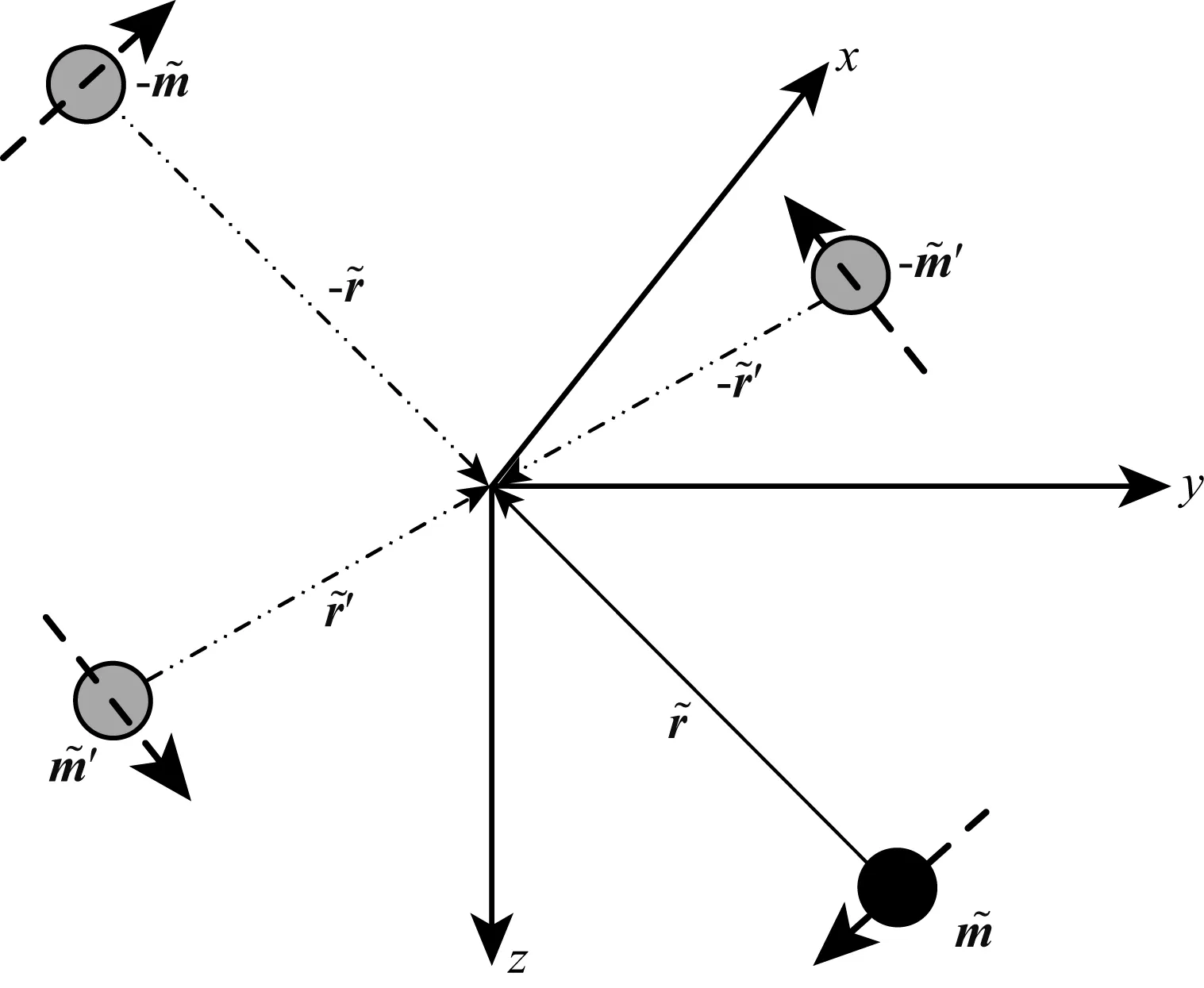
图2　几何不变量3表示的磁矩及位置矢量示意图Fig.2　Inverse solution of source-dipole vector and magnetic moment based on geometric invariant 3

由图2可知，该方法得到真实位置及磁矩矢量的同时，也得到了3个虚假解，因此，在实际应用中，可根据所测目标在磁梯度张量系统的上方或下方，直接去除两个虚假解，然后根据磁梯度张量系统测得的多点总磁场强度及磁矢量场进行另一个虚假解的去除，进而实现真实磁偶极子位置及磁矩矢量的正确反演.

4仿真实验分析

利用本文提出的几何不变量进行磁偶极子位置及磁矩矢量反演的三组仿真实验，以验证所提几何不变量的准确性.其中磁梯度张量系统位于坐标原点，磁偶极子运动轨迹的具体参数设置如表1所示.仿真实验流程如下：

(1)根据磁偶极子数学模型，计算磁偶极子位于不同位置时在坐标原点产生的磁梯度张量值.

(2)对计算得到的磁梯度张量数据进行特征值分析，求解其对应的特征值和特征向量.

表1　仿真参数设置

(3)利用公式(12)求解磁偶极子相对于测量点的距离及磁矩模.

(4)将计算得到的特征值及特征向量代入式(19)及式(20)，求解磁偶极子位置及磁矩矢量.

利用本文所提几何不变量反演得到的磁偶极子在x-y平面上的运动轨迹如图3—5所示.由图可知，几何不变量估计得到磁偶极子真实运动轨迹的同时也求解得到3个虚假解，必须采用有效方法准确去除虚假解.虚假解的去除流程如图6所示，去除虚假解后的真实轨迹在图3—5中以深色表示.

图3　估计得到的磁偶极子运动轨迹(仿真实验1)Fig.3　Estimated track of magnetic dipole coming from the first simulation

由于在实际应用中所探测目标在测量平面的上方或下方为已知信息，且单点测量的数据反演得到的四组磁偶极子的三维坐标关于原点对称，因此，根据已知信息中的Z坐标信息可直接删除四组解中的两个虚假解.将剩下的两组解代入式(3)和式(4)中可计算得到两组不同的解在测量点产生的磁梯度张量值.若为真实解，则该计算值与实际测量值相吻合；若为虚假解，则计算得到的张量数据与测量数据存在较大的偏差，因此，根据计算值与测量值之间的差异可进一步去除第3个虚假解，进而得到真实的磁偶极子位置及磁矩矢量.值得注意的是，虚假解的去除是实时的，即每个测量点反演得到的四组解都需要进行虚假解的去除.

图4　估计得到的磁偶极子运动轨迹(仿真实验2)Fig.4　Estimated track of magnetic dipole coming from the second simulation

图5　估计得到的磁偶极子运动轨迹(仿真实验3)Fig.5　Estimated track of magnetic dipole coming from the third simulation

图6　虚假解去除流程Fig.6　Flow chart of elimination of ghost solutions

图7　存在测量噪声时估计得到的磁偶极子运动轨迹Fig.7　Estimated track of magnetic dipole existing measurement noises

由于在实际应用中，磁梯度张量系统存在测量误差将在一定程度上影响磁偶极子探测和位置反演的距离，因此，将上述理论模型仿真中加入随机噪声进行研究.考虑真实磁梯度张量系统多用来测量5个独立的磁梯度张量分量及张量矩阵对称的原则，在5个独立的磁梯度张量分量信号中加入均值为0 nT·m-1，方差为0.5 nT·m-1的高斯白噪声.图7为表1中第一组仿真实验加入噪声后的运动轨迹反演结果.由图可知，加入随机噪声后，磁偶极子的可跟踪范围为y轴方向上的[-20 m,20 m].在可跟踪范围内，本文所提算法可较为准确地跟踪磁偶极子，而超出此跟踪范围后，反演得到的磁偶极子的位置坐标存在较大的偏差和不确定性，反演结果无法为磁偶极子的运动轨迹提供参考.同样地对表1中的第二及第三组仿真实验加入随机噪声，则第二组仿真实验的可跟踪的坐标范围为[-20,-5]至[8,23]，第三组仿真实验的可跟踪的坐标范围为[0,-25]至[-22,-14].由式(3)及式(4)可知，磁矢量信号及磁梯度张量信号随着距离的增加衰减极为迅速，因此，距离磁偶极子目标较远处的磁场信号较弱，有效信号可能被测量噪声所淹没，进而反演的得到的磁偶极子位置及磁矩矢量存在较大的偏差.即在实际应用中，磁偶极子的跟踪距离不仅仅受到其自身磁矩大小的影响，还受到测量系统中测量噪声的影响.

5实验验证

为验证本文所提几何不变量在磁性目标定位及跟踪中的可行性，采用4个磁通门传感器构建了平面十字形磁梯度张量系统进行实验研究.实验时某铁磁性运动载体(在测量范围内可近似等效为磁偶极子)以60 km·h-1的速度在道路上直线运动，磁梯度张量系统放置于道路一侧的地面上，同步采集各传感器的输出数据，采样频率为2048 Hz.选取两条行驶路线进行目标轨迹的估计，假设运动载体沿着y轴正方向前进，在x方向上距离磁梯度张量系统的距离(Closest Proximity Approach, CPA)分别为1.4 m和2 m，z轴方向竖直向下构建右手坐标系进行数据计算和分析.

由于磁梯度张量系统静止不动，因此可在无磁性目标的情况下采集背景地磁场，实时采集得到的磁传感器数据减去背景地磁场即为磁性目标产生的磁场数据.在此，利用总磁场强度的变化判断是否有磁性目标的出现，然后截取采集得到的实时信号进行运动轨迹的估计.由于运动载体等效的磁偶极子位于测量系统的上方，可直接去除两个虚假解，则反演得到的载体在x-y平面的运动轨迹如图8、图9所示.利用图6所示的方法去除剩余的虚假解，则图8、图9所示右侧深色曲线为估计得到的运动轨迹的真实解.

由图8和图9可知，虚假解表示的铁磁体运动轨迹与真实运动轨迹相差较大，利用图6所示的虚假解去除流程有效地识别出了由磁梯度张量数据计算得到的真实解.在可探测范围内，利用几何不变量估计得到的铁磁性载体运动轨迹的真实解可较好地跟踪运动载体的实际轨迹，可实现基于磁梯度张量数据的运动载体实时跟踪.由于磁传感器自身的噪声以及实验场地中地磁梯度的存在，导致估计得到的目标位置与真实值存在一定的偏差，可通过进一步提高磁传感器的精度实现目标的远距离跟踪.

图8　估计得到的载体运动轨迹(CPA=1.4 m)Fig.8　Estimated track of mobile vehicle when CPA equal to 1.4 m

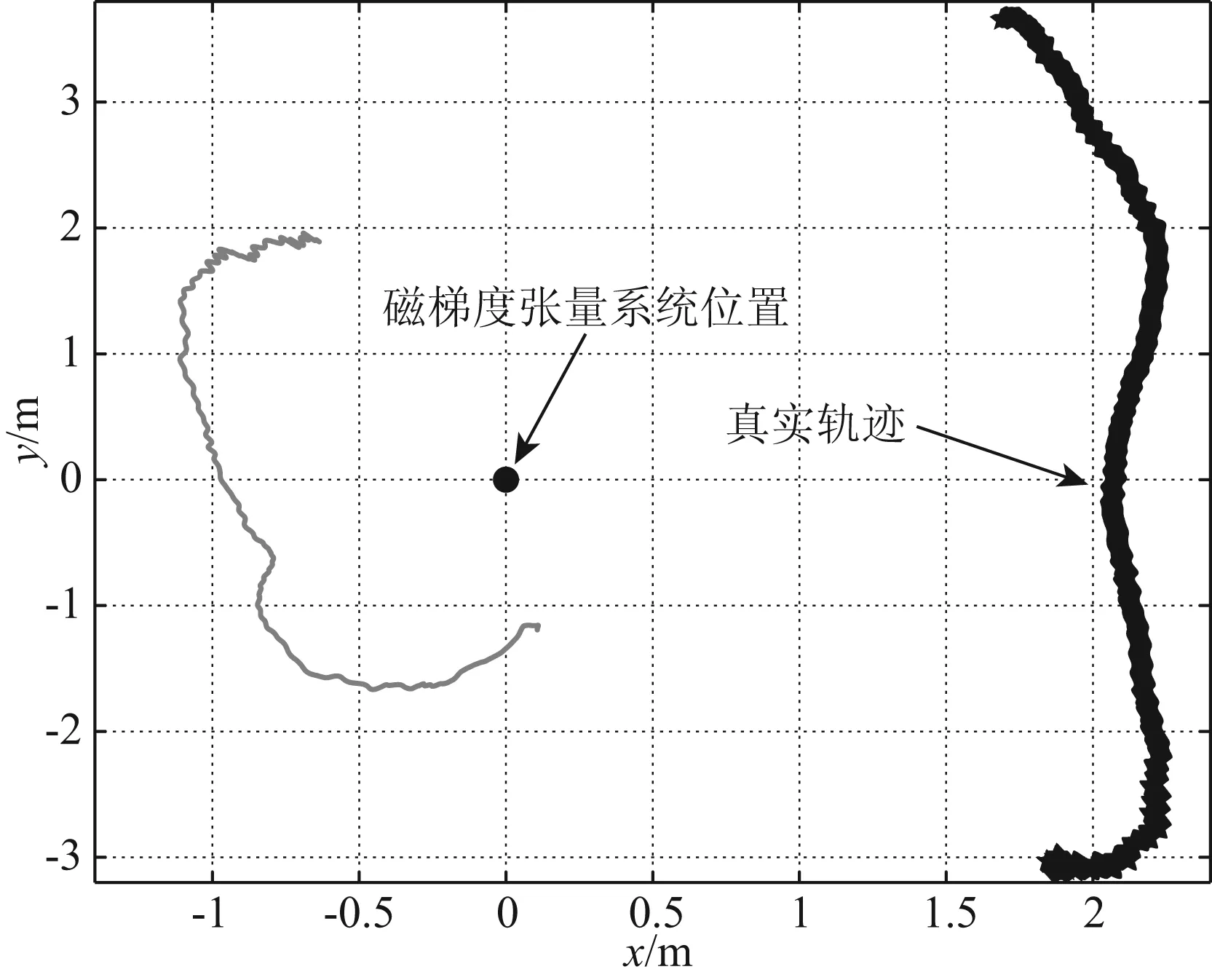
图9　估计得到的载体运动轨迹(CPA=2 m)Fig.9　Estimated track of mobile vehicle when CPA equal to 2 m

6结论

(1) 基于数学解析方法对磁偶极子产生的磁梯度张量矩阵的特征值及特征向量进行了理论推导，得出了磁偶极子位置矢量与磁矩矢量间的夹角关于特征值的数学表达式，并在此基础上给出了磁矩模及磁偶极子与测量点间的距离的求解公式.

(2) 基于磁偶极子产生的矢量场、磁梯度张量场及其欧拉反褶积公式，验证了磁偶极子位置矢量、磁矩矢量、最大特征值对应的特征向量及最小特征值对应的特征向量共面的假设，并给出了位置矢量及磁矩矢量关于特征值及特征向量的数学表达式.

(3) 对本文提出的几何不变量在磁性目标跟踪上的应用进行了仿真和实测分析，实验结果证明了公式推导的正确性及其在目标跟踪中的实用性.

致谢笔者向匿名评审专家及编辑部老师致以谢意！

References

Bian G L, Zhai G J, Fan L, et al. 2011. Applying two-step iterative least square approach to determine the geometry and physical parameters of magnetic sphere sources.ChineseJ.Geophys. (in Chinese), 54(5): 1375-1383, doi: 10.3969/j.issn. 0001-5733.2011. 05.027.

Ma G Q, Du X J, Li L L. 2012. Comparison of the tensor local wavenumber method with the conventional local wavenumber method for interpretation of total tensor data of potential fields.ChineseJ.Geophys. (in Chinese), 55(7): 2450-2461, doi: 10.6038/j.issn.0001-5733. 2012.07.029.

Nara T, Suzuki S, Ando S. 2006. A closed-form formula for magnetic dipole localization by measurement of its magnetic field and spatial gradients.IEEETransactionsonMagnetics, 42(10): 3291-3293.

Nara T, Ito W. 2014. Moore-Penrose generalized inverse of the gradient tensor in Euler's equation for locating a magnetic dipole.JournalofAppliedPhysics, 115: 17E504.

Reid A B, Allsop J M, Granser H, et al. 1990. Magnetic interpretation in three dimensions using Euler deconvolution.Geophysics, 55(1): 80-91.

Rim H, Park Y S, Jung H K. 2012. Interpretation of magnetic gradient tensor for automatic locating a dipole source.∥ 22ndInternational Geophysical Conference and Exhibition. Australia, 1-3. Schmidt P W, Clark D A. 2000. Advantages of measuring the magnetic gradient tensor. Preview: Australian Society of Exploration Geophysicists, 85: 26-30.Schmidt P W, Clark D A. 2006. The magnetic gradient tensor: its properties and uses in source characterization.TheLeadingEdge, 25(1): 75-78.

Yu T Q, Mao W M. 2006. Tensor Analysis and Application (in Chinese). Beijing: Tsinghua University Press.

Zhang C D. 2006. Airborne tensor magnetic gradiometry—the latest progress of airborne magnetometric technology.ChineseJournalofEngineeringGeophysics(in Chinese), 3(5): 354-361.Zhang C D. 2007. Some problems concerning the magnetic anomaly detection (MAD).ChineseJournalofEngineeringGeophysics(in Chinese), 4(6): 549-553.

Zhang C Y, Xiao C H, Gao J J, et al. 2010. Experiment research of magnetic dipole model applicability for a magnetic object.JournalofBasicScienceandEngineering(in Chinese), 18(5): 862-868.

Zhang F X, Zhang F Q, Meng L S, et al. 2007. Magnetic potential spectrum analysis and calculating method of magnetic anomaly derivatives based on discrete cosine transform.ChineseJ.Geophys. (in Chinese), 50(1): 297-304.

Zhang G, Zhang Y T, Fan H B, et al. 2013a. The effect of vehicle attitude variation on magnetic field gradient tensor localization precision for invisible object.JournalofDetection&Control(in Chinese), 35(1): 20-24.

Zhang G, Zhang Y T, Li Z N, et al. 2013b. Localizing method of magnetic field gradient tensor under carriers moving parallelly.JournalofHuazhongUniversityofScienceandTechnology(NatutalScienceEdition) (in Chinese), 41(1): 21-24.

附中文参考文献

卞光浪, 翟国君, 范龙等. 2011. 用最小二乘两步迭代法求解磁性球体几何与磁性参数. 地球物理学报, 54(5): 1375-1383, doi: 10.3969/j.issn.0001-5733.2011.05.027.

马国庆, 杜晓娟, 李丽丽. 2012. 解释位场全张量数据的张量局部波数法及其与常规局部波数法的比较. 地球物理学报, 55(7): 2450-2461, doi: 10.6038/j.issn.0001-5733.2012.07.029.

余天庆, 毛为民. 2006. 张量分析及应用. 北京: 清华大学出版社.

张昌达. 2006. 航空磁力梯度张量测量-航空磁测技术的最新进展. 工程地球物理学报, 3(5): 354-361.

张昌达. 2007. 关于磁异常探测的若干问题. 工程地球物理学报, 4(6): 549-553.

张朝阳, 肖昌汉, 高俊吉等. 2010. 磁性物体磁偶极子模型适用性的试验研究. 应用基础与工程科学学报, 18(5): 862-868.

张凤旭, 张凤琴, 孟令顺等. 2007. 基于离散余弦变换的磁位谱分析及磁异常导数计算方法. 地球物理学报, 50(1): 297-304.

张光, 张英堂, 范红波等. 2013a. 载体姿态变化对磁张量定位精度的影响. 探测与控制学报, 35(1): 20-24.

张光, 张英堂, 李志宁等. 2013b. 载体平动条件下的磁梯度张量定位方法. 华中科技大学学报(自然科学版), 41(1): 21-24.

(本文编辑汪海英)

基金项目军内科研资助.

作者简介尹刚，男，1988年生，博士生，主要研究方向为磁异常探测、磁梯度张量测量及地磁导航.E-mail: gang.gang88@163.com *通讯作者张英堂，男，1960年生，教授，博士生导师，主要研究方向为测试技术与信号处理.E-mail: zyt01@malis.tsinghua.edu.cn

doi:10.6038/cjg20160232 中图分类号P631

收稿日期2014-06-16，2015-12-23收修定稿

Research on geometric invariant of magnetic gradient tensors for a magnetic dipole source and its application

YIN Gang, ZHANG Ying-Tang*, LI Zhing-Ning, ZHANG Guang, FAN Hong-Bo

Department7th，MechanicalEngineeringCollege，Shijiazhuang050003，China

AbstractAs attitude change of the magnetic gradient tensor system may affect precision of gradient measurements and data interpretation, the rotational invariants which are invariant under rotation of the reference frame have been extensively studied for magnetic gradient tensor data. Based on the eigenvalue analysis of magnetic gradient tensors produced by the magnetic dipole, some invariant geometrical relationships, which are defined as geometric invariants, are deduced in this paper. Firstly, the eigenvector corresponding to the eigenvalue which has the smallest absolute value is perpendicular to both the dipole moment and source-dipole displacement vector. Secondly, source-dipole displacement, dipole moment and eigenvectors corresponding to the maximal and minimal eigenvalues are coplanar. Thirdly, the angle between dipole moment and source-dipole displacement vector can be calculated by eigenvalues of magnetic gradient tensors. At last, the proposed geometric invariants are used to track a magnetic target, and simulation and experimental results confirm the correctness and practicability of the proposed geometric invariants.

KeywordsMagnetic dipole; Magnetic gradient tensor; Geometric invariant; Eigenvalue; Tensor invariant

尹刚， 张英堂， 李志宁等. 2016. 磁偶极子梯度张量的几何不变量及其应用.地球物理学报，59(2):749-756,doi:10.6038/cjg20160232.

Yin G, Zhang Y T, Li Z N, et al. 2016. Research on geometric invariant of magnetic gradient tensors for a magnetic dipole source and its application.ChineseJ.Geophys. (in Chinese),59(2):749-756,doi:10.6038/cjg20160232.