NOFRFs频谱散度Bootstrap分析法辨识旧零件内部损伤

马少花,毛汉领,毛汉颖,黄振峰,李欣欣

(1.广西大学机械工程学院, 广西南宁530004；2.广西科技大学汽车与交通学院, 广西柳州542506)



NOFRFs频谱散度Bootstrap分析法辨识旧零件内部损伤

马少花1,毛汉领1,毛汉颖2,黄振峰1,李欣欣1

(1.广西大学机械工程学院, 广西南宁530004；2.广西科技大学汽车与交通学院, 广西柳州542506)

摘要：旧零件内部损伤的检测与辨识是再制造工程的关键热点问题。针对旧零件内部损伤的非线性，采用锤击法激励旧零件，获取输入/输出信号，进而估算旧零件的多阶非线性输出频率响应函数NOFRFs，并构建反映NOFRFs频谱差异度的散度指标(divergence index, DI)作为敏感故障特征量来实现对旧零件内部损伤的检测与辨识。为了提高统计分析精度，引入Bootstrap方法对敏感故障特征量进行统计分析。首先，估算不同状态的系统NOFRFs；然后，计算NOFRFs散度指标DI，并利用Bootstrap方法对其进行统计分析，获取指标的均值和置信率为95%的样本区间；最后，计算被测零部件的′，并依据′所落的样本区间，推断被测零部件的损伤情况。将该法应用于不同使用时长的旧连杆的损伤检测中，结果表明，能以95%的置信率推断被测连杆的工作时长为296 h，实查为288 h，准确率较高。该研究为实际工程中旧零件内部损伤程度的检测及识别提供了一种全新的有效方法。

关键词：NOFRFs;散度;Bootstrap法;锤击试验;损伤检测

0引言

旧零件隐藏的内部损伤累积最终会导致零件的失效甚至突然破坏、造成巨大损失，因此对旧零件内部损伤的准确检测与辨识至关重要。为此，亟需一种准确、高效的内部损伤检测方法来实现对再制造旧零件的检测和分类。

研究表明，系统或零部件出现损伤后往往表现出非线性。由Volterra级数理论推导出的非线性输出频率响应函数(NOFRFs)能较好的反映受损伤系统的非线性特性，基于NOFRFs构建对系统非线性参数敏感的特征量是损伤特征提取的一种有效方法。Peng等[1]指出在合适的激励下，NOFRFs对梁的裂纹敏感，可将计算得到的NOFRFs值作为衡量裂纹大小的指标，裂纹越大，NOFRFs值越大。Peng等[2-4]利用多阶NOFRFs值之间的关系实现了对一维循环结构损伤位置的检测。员险峰和李志农等[5-6]通过比较裂纹转子系统的各阶NOFRFs值实现了对单裂纹转子的裂纹位置和裂纹深度的有效检测。韩清凯等[7]基于NOFRFs实现了对转子系统的碰磨故障定位的识别。鉴于NOFRFs是频率的一维函数，直接对比各阶NOFRFs值进行损伤检测并不方便，Peng和Lang等[8]基于NARMAX模型辨识NOFRFs，并提出了NOFRFs指标Fe。每阶NOFRF仅对应一个Fe值，故而可较方便的实现损伤检测。程长明等[9]利用前述NARMAX和NOFRFs指标Fe实现了对桥梁模型结构的损伤判别。然而NOFRFs指标Fe只对显性微裂纹的损伤较敏感，无法对累积疲劳或隐性微裂纹进行检测。

锤击法操作简便，在实际工程中应用广泛。龙国平等[10]利用锤击法实现了对大型水电站水轮机导叶部件的固有频率的分析。基于此，本文利用锤击法获取系统输入、输出信号，并直接估算系统的NOFRFs。J散度具有对称性，可表征两分布之间的差异，还可定量表达两频域谱图之间的差异。郭艳平等[11]利用经验模态分解(Empirical Mode Decomposition, EMD)和散度指标实现了对滚动轴承不同故障状态的识别，他们首先对采集的振动信号进行EMD处理并选取包含故障信息的本征模函数(Intrinsic Mode Function, IMF)进行重构，对重构后IMF信号进行Hilbert包络分析，进而利用散度指标提取故障特征量，最终通过对比故障特征量的变化实现故障状态识别；苗刚[12]基于J散度理论提出了一种针对往复压缩机的故障分类方法，该法通过比较待检样本与已建立的标准样本之间的J散度值，并结合预先设定的J散度阈值，实现对被测样本的分类。研究表明，通过对振动信号进行处理，并提取散度特征量，进而实现故障诊断，是一种非常有效的故障识别方法。NOFRFs是基于系统激励、响应信号估算而来的，可以很好的表征非线性系统的本质特性，相当于非线性系统的“传递函数”，但至今未见基于NOFRFs散度的研究。

基于Bootstrap理论，对实际工程中机械设备或系统的故障特征量进行统计分析，进而实现故障诊断和状态识别的案例不在少数，比如姚良等[13]将信号的加权时域同步平均处理方法与Bootstrap方法相结合，实现了对柴油机供油系统的状态监测和故障诊断；刘刚等[14]通过提取实测振动信号的功率谱谱峰特征量，并利用Bootstrap方法对该特征量进行统计分析，进而实现了火车车轮系统滚动轴承的故障状态识别；李涛等[15]利用Bootstrap方法通过对气阀缸盖的故障特征参数的统计计算和分析，实现了对气阀缸盖的故障诊断和状态识别；许平等[16]充分利用Bootstrap方法可对小样本数据进行统计分析的优势，选用Bootstrap方法实现了对气门机构的故障样本库的高效、准确构建。借助于Bootstrap方法，可对实际中获取的少量试验数据进行统计分析，这恰恰解决了实际工程中较难获取大量数据的问题。因此，通过引入Bootstrap方法，对NOFRFs故障特征指标进行统计分析，将是一个全新的思路。

本文将对不同裂纹损伤的三点弯曲标准试件以及不同工作时长的旧连杆进行了试验和分析，以验证该方法在检测和辨识旧零件内部损伤时的有效性和准确性。

1基于NOFRFs的散度特征提取方法

1.1NOFRFs及其频谱分析

NOFRFs是由Volterra级数发展而来的，可较好的表征系统的本质特性，且物理意义明确，在故障诊断领域得到了广泛的应用。NOFRFs定义[11]为：

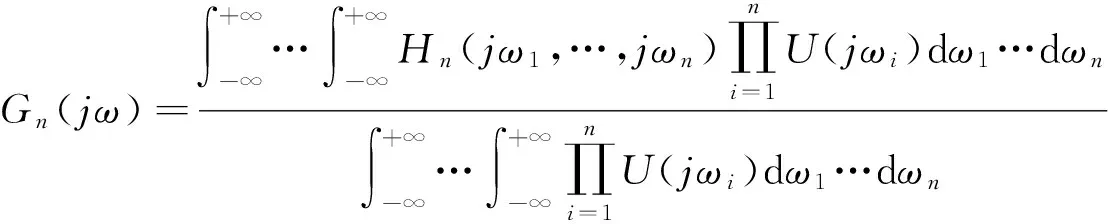
(1)

各阶NOFRFs都是频率的一维函数，方便显示和分析，且较易由系统输入输出辨识得到。文献[1]给出了一种直接由输入/输出信号辨识系统前N阶NOFRFs的方法，该法只需激励系统N次，便可估算其前N阶NOFRFs。由于系统的前四阶NOFRFs便可很全面的描述系统，因此实际应用中一般只计算前四阶NOFRFs。

对任意一个可由Volterra级数表示的系统，其输出谱可表示为：

Y(jω)=G1(jω)U1(jω)+G2(jω)U2(jω)+…+Gn(jω)Un(jω)，

其一阶NOFRFsG1(jω)表征系统的线性特性，高阶NOFRFsGn(jω),(n=2,3，…)表征系统非线性特性。当系统发生损伤后会表现出非线性，相应的其高阶NOFRFs值就会增大；损伤越严重，非线性特征越明显，高阶NOFRFs值就越大。从NOFRFs频谱角度分析，即系统发生损伤前后，多阶NOFRFs频谱的谱线幅值之和会发生变化。换言之，即损伤系统和正常系统的多阶NOFRFs的频谱存在差异，且损伤越严重，两系统的各阶NOFRFs谱图差异越明显。

1.2NOFRFs的散度特征提取

J散度是一种非常有效的距离度量方式。它既可以用来定量表达两个分布之间的差异，也可以表达两个时间序列之间的差异，在频域中还可以表示两个谱图之间的差异。文献[12]利用J散度模式分类法实现了对往复式压缩机气阀的故障诊断。文献[11]基于EMD和散度指标对滚动轴承故障进行分析，结果表明J散度不仅可表征滚动轴承的故障类型，还对故障损伤程度较为灵敏。J散度的定义[14]为：

(2)

其中，K为谱图上等分的频率间隔的数目，S1、S2为两个谱图，S1j、S2j为谱图中第j个频率间隔内的谱线幅值的总和。由定义式(2)可知：①J(S1,S2)是非负的；②当两张谱图完全相同时，其J散度等于零；③两张谱图间的差异性越大，J散度也越大。

系统发生故障后，多阶NOFRFs谱图将会发生变化。基于J散度可定量表示两频谱图之间的差异这一特性，本文给出了一种基于NOFRFs频谱的散度指标(Divergence Index， DI)，用于评价两个不同系统(被测系统和正常系统)的各阶NOFRFs频谱之间的差异，其定义如下：

(3)

其中，N为估算的系统NOFRFs的阶数，A1n、A2n分别为正常系统、被测系统的第n阶NOFRFs的在频域的积分，即

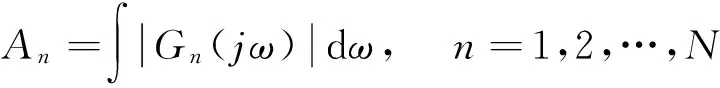
NOFRFs的散度指标DI刻画了被测系统的NOFRFs谱图与正常系统的相应阶NOFRFs谱图之间的差异。两系统NOFRFs的散度指标DI越小，表明被测系统的各阶NOFRFs谱图与正常系统的差异越小，即被测系统的损伤越小；反之，DI越大，两系统的各阶NOFRFs谱图差异越大，被测系统损伤越严重。

为了提高利用散度指标DI进行损伤识别的稳定性和准确性，可对计算的多个DI进行平均处理，即

(4)

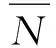
2损伤检测方法介绍

利用统计分析法可以对系统的统计特征量及其分布的不确定性进行评价。研究表明[13-14]，平均幅值、标准差、峭度等数学统计量指标通常可很好地反映结构或机械零部件状态的变化。然而在结构或零部件诊断过程中，我们很难获得足够的样本数据，这就给估计特征量指标的统计特性及评价诊断的有效性造成了困难。1979年美国斯坦福大学统计系教授Efron.B提出了Bootstrap方法[17]，该法通过对原始数据进行间接反复采样，实现了对样本容量的扩充，从而可计算某一统计量的均值、标准差、概率分布等。

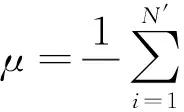
2.1基于Bootstrap方法计算指标DI的均值和置信区间

下面以15次锤击测试为例，详细介绍锤击激励下基于NOFRFs散度指标和Bootstrap方法的损伤检测实施步骤，如图1所示。

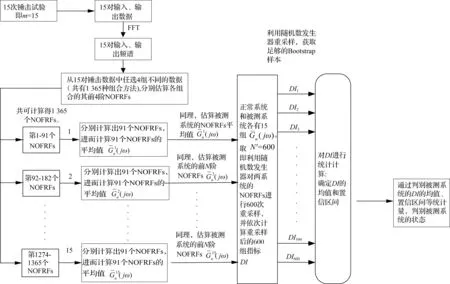
图1　基于Bootstrap方法的NOFRFs散度指标DI的计算过程

2.2损伤判别过程

3可行性试验研究

本试验采用锤击法，试验装置包括美国PCB力锤086c04(自带力传感器)、美国IMI加速度传感器604B11/M006 JW、北京京南MDR-80移动数据记录仪和IMAS_4.20信号采集分析系统等，试验平台如图2所示。

试验对象为根据某疲劳试验机设计的三点弯曲标准试件，其材料为45号钢，尺寸为：长260 mm、宽60 mm、高15 mm。用线切割机在标准试件的相同位置分别预制不同深度的裂纹，以模拟该批试件的不同损伤情况，并定义裂纹深度与试件宽度的比值为裂纹率α。为对本文所提出的损伤检测方法进行可行性研究，试验时将试件分为两大组：一组为样本组，用于确定该批试件的各状态间指标DI的样本区间，样本组包括正常试件(记为Norm)、裂纹损伤试件1(记为Dam1，裂纹率α=0.167)、裂纹损伤试件2(记为Dam2，裂纹率α=0.250)、裂纹损伤试件3(记为Dam3，裂纹率α=0.333)，如图3所示；另一组为被测组试件(记为Test1)，用于检验前述损伤检测方法的有效性。

图2锤击试验平台

Fig.2Impact excitation test platform

图3三点弯曲标准试件——样本组

Fig.3Three point bending standard specimen——samples

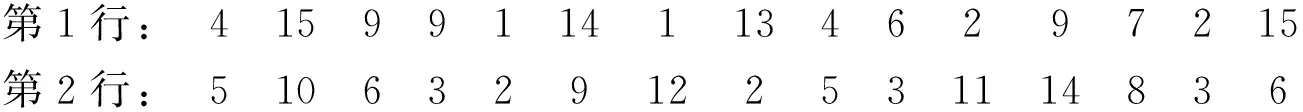
表1　基于Bootstrap计算的NOFRFs散度指标DI

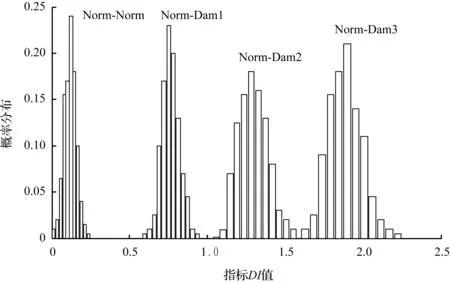
图4　NOFRFs散度指标DI的平均值分布

状态Norm-NormNorm-Dam1Norm-Dam2Norm-Dam3均值0.12650.76421.30971.8859方差0.41630.57550.83520.7627置信区间[0.0449,0.2081][0.6514,0.8770][1.1460,1.4734][1.7364,2.0354]

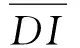
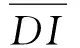
表3　NOFRFs散度指标DI的均值和置信区间(被测组)

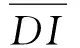
图5　不同状态的样本组连杆Fig.5　The connecting rod of different condition (samples)

4实例分析

将本文所提方法应用到某再制造厂的一批旧连杆的损伤检测中。该批连杆是从某型柴油机拆卸下来的，连杆型号相同，且材质均为40Cr。取6组不同工作时长的连杆用于试验，其中一组为样本组，包括未使用的新连杆(记为NL)、使用时长200 h的连杆(记为DL1)、使用时长296 h的连杆(记为DL2)、使用时长450 h的连杆(记为DL3)，如图5所示；另一组为被测组连杆：被测连杆1′(记为TL1)、被测连杆2′(记为TL2)，被测组连杆使用时长未知。

表4　NOFRFs散度指标DI的均值和置信区间(样本组)

对被测连杆进行锤击试验，并计算它与样本组新连杆之间的NOFRFs散度指标DI。经多次重采样得到指标DI的均值及95%的置信区间如表5所示。

表5　NOFRFs散度指标DI的均值和置信区间(被测组)

5结论

参考文献：

[1]PENG Z K, LANG Z Q, BILLINGS S A.Crack detection using nonlinear output frequency response functions[J]. Journal of Sound & Vibration, 2007, 301(3-5):777-788.

[2]PENG Z K, LANG Z Q.Detecting the position of non-linear component in periodic structures from the system responses to dual sinusoidal excitations[J]. International Journal of Non-Linear Mechanics, 2007, 42(9):1074-1083.

[3]PENG Z K, LANG Z Q, BILLINGS S A.A novel method for detecting the nonlinear components in periodic structures[J]. Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2008, 222:903-910.

[4]PENG Z K, MENG G, LANG Z Q, et al.On the distribution of nonlinear effects in locally nonlinear one-dimensional chain type structures[J]. International Journal of Mechanical Sciences, 2011, 53(3):226-235.

[5]员险锋.基于非线性输出频率响应函数的转子裂纹故障诊断方法研究[D]. 郑州：郑州大学, 2011.

[6]员险锋,李志农,林言丽.基于非线性输出频率响应函数的裂纹故障诊断方法研究[J]. 机械强度, 2013, 35(2):133-137.

[7]韩清凯,杨英,郎志强,等.基于非线性输出频率响应函数的转子系统碰摩故障的定位方法研究[J]. 科技导报,2009,27(2):29-32.

[8]PENG Z K, LANG Z Q, WOLTERS C, et al.Feasibility study of structural damage detection using NARMAX modelling and nonlinear output frequency response function based analysis[J]. Mechanical Systems & Signal Processing, 2011,25(3):1045-1061.

[9]程长明,彭志科,孟光.基于NARMAX模型和NOFRF结构损伤检测的实验研究[J]. 动力学与控制学报, 2013, 11(1):89-96.

[10]龙国平,熊焕庭,毛汉领.用锤击法实测大型工程结构的固有频率[J]. 广西大学学报(自然科学版), 1999, 24(2):148-150.

[11]郭艳平,颜文俊,包哲静,等.基于经验模态分解和散度指标的风力发电机滚动轴承故障诊断方法[J]. 电力系统保护与控制, 2012，40(17):83-87.

[12]苗刚,马孝江,任全民.基于J散度的模式分类方法在故障诊断中的应用[J]. 中国机械工程, 2007, 18(4):431-433.

[13]姚良,成曙,张振仁,等.基于加权时域同步平均与Bootstrap方法的柴油机供油系统故障诊断[J]. 机械科学与技术, 2007, 26(12):1584-1587.

[14]刘刚, 屈梁生.应用Bootstrap方法构造机械故障特征库[J]. 振动工程学报, 2002, 15(1):106-110.

[15]李涛,李艾华,徐斌,等.统计模拟在气阀机构故障诊断中的应用[J]. 内燃机工程, 2005, 26(2):72-75.

[16]许平,李涛,张振仁.基于Bootstrap方法构造故障特征库的研究[J]. 小型内燃机与摩托车, 2003, 32(6):10-12.

[17]EFRON B.Computers and the theory of statistics: thinking the unthinkable[J]. SIAM Review,1979,4:460-480.

(责任编辑梁健)

收稿日期：2016-03-27；

修订日期：2016-04-02

基金项目：国家自然科学基金资助项目(51365006, 51445013)；广西制造系统与先进制造技术重点实验室课题(14-045-15S05)

通讯作者：毛汉领(1963—)，男(瑶族)，广西恭城人，广西大学教授，博士生导师，博士；E-mail：maohl79@gxu.edu.cn。

doi:10.13624/j.cnki.issn.1001-7445.2016.0729

中图分类号：TH17

文献标识码：A

文章编号：1001-7445(2016)03-0729-09

Internal damage identification for used parts based on NOFRFs divergence index and bootstrap method

MA Shao-hua1, MAO Han-ling1, MAO Han-ying2, HUANG Zhen-feng1,LI Xin-xin1

(1.College of Mechanical Engineering, Guangxi University, Nanning 530004，China;2.College of Automobile and Transportation, Guangxi University of Science and Technology,Liuzhou 542506，China)

Abstract:Detection and identification of internal damage for used parts is a hot spot of remanufacturing engineering. In view of nonlinearity of internal damage, the input and output signals are collected by impact excitation tests, NOFRFs of used parts are estimated, and the divergence index DI reflecting the discrepancy between frequency spectrums of different NOFRFs is built, then the internal damage identification for used parts is conducted by comparing the values of index DI. In order to improve the analysis precision, the approach of Bootstrap is applied. Firstly, estimate NOFRFs of different systems; then, calculate the NOFRFs divergence index DI, and analyze statistically the values of DI by using Bootstrap method to acquire the average and 95% sample interval of index DI; finally, calculate the NOFRFs divergence index ′ between the tested part and the normal part, infer the damage states of the tested parts according to the relationship between the values of ′ and the before-mentioned sample interval. The proposed approach was applied to the damage detection of the used connecting rods, and then the running hour of tested rod was extrapolated for 296 h by test analysis. It’s ascertained that the actual running hour of the tested rod is 288 h, which demonstrates the veracity of the proposed method. The study proposes a new effective method to the internal damage identification for used parts in practical engineering.

Key Words:NOFRFs; divergence; Bootstrap approach; impact excitation test; damage detection

引文格式： 马少花,毛汉颖，毛汉颖，等.NOFRFs频谱散度Bootstrap分析法辨识旧零件内部损伤[J].广西大学学报(自然科学版)，2016，41(3)：729-737.