空间钢构架—钢管混凝土短柱轴压承载力计算方法

李伟强，唐兴荣，贾　欢

(苏州科技大学江苏省结构工程重点实验室， 江苏苏州215011)



空间钢构架
—钢管混凝土短柱轴压承载力计算方法

李伟强，唐兴荣，贾欢

(苏州科技大学江苏省结构工程重点实验室， 江苏苏州215011)

摘要：为了研究新型空间钢构架—钢管混凝土短柱的轴压极限承载力的计算方法，分析了空间钢构架—钢管混凝土轴压短柱的约束作用机理，在已有试验研究和有限元非线性分析的基础上，采用叠加法并考虑空间钢构架对钢管外混凝土的约束作用和钢管对核心混凝土的约束作用，建立了空间钢构架—钢管混凝土轴压短柱的极限承载力计算公式，其计算值与试验值符合较好，可以较好地计算空间钢构架—钢管混凝土短柱的轴压极限承载力。

关键词：组合柱；轴压极限承载力；约束效应；空间钢构架混凝土；钢管混凝土

0引言

(超)高层建筑高度的不断增大对柱子的承载力和延性性能提出了更高的要求。钢—混凝土组合柱,特别是组合柱中的钢管混凝土柱、钢骨混凝土柱因具有承载力高、延性好的特点，已得到了广泛应用和深入研究。钢管混凝土柱具有延性好、承载力高、经济效果好、施工方便等优点[1-7]，但梁柱节点的处理比较复杂，而且它的耐火性能相对较差，必须采取一定的防火措施[8]。为了弥补钢管混凝土柱的不足，国内学者提出了以钢管混凝土为核心、钢管外侧配置普通钢筋并浇筑混凝土以形成钢管混凝土核心柱[9-11]。与钢管混凝土柱相比，这种组合柱内的钢管混凝土芯柱由于尺寸比较小，容易穿过梁柱节点，使得节点区的梁柱配筋构造处理非常简单，但也存在核心钢管混凝土与外围普通钢筋混凝土在力学性能上的不协调，核心钢管混凝土的性能明显优于钢管外围普通钢筋混凝土。空间钢构架是由纵向弦杆(角钢)、斜向缀条或横向缀条焊接而成的承重轻钢结构，将空间钢构架代替传统的绑扎钢筋骨架，可形成空间钢构架混凝土结构构件。已有的试验研究[12-14]表明，在轴向压力作用下，空间钢构架对内部混凝土具有一定的约束作用，使核心约束区的混凝土处于三向受压的状态，其塑性、强度和韧性性能大为提高。空间钢构架的约束作用增强了柱子的抗弯、抗扭的能力，提高柱子的延性指标，有利于结构的抗震。

基于上述背景，利用空间钢构架对核心混凝土的约束作用，在空间钢构架混凝土柱的核心内埋钢管混凝土，形成空间钢构架—钢管混凝土柱。这种新型的组合柱形式 [图1(a)]由核心钢管混凝土[图1(c)]和钢管外空间钢构架混凝土[图1(b)]两部分组成。显然，这种新型组合柱具有钢管混凝土核心柱的优点，同时，由于空间钢构架对钢管外混凝土的约束作用，有可能使钢管内外的混凝土(空间钢构架约束混凝土、钢管核心混凝土)的性能保持协调，柱子的力学性能将得到改善。但目前对空间钢构架—钢管混凝土柱的试验研究和理论分析还较少[15-17]，尚需要进一步开展对其全面的试验研究和理论分析。

本文是建设部科研项目(99-031-2)的拓展性研究，通过分析轴心受压下空间钢构架—钢管混凝土柱的约束作用机理，推导了內埋钢管混凝土短柱轴压承载力和钢管外空间钢构架混凝土短柱轴压承载力的计算公式，采用叠加法并考虑空间钢构架约束混凝土和钢管约束混凝土的特点，建立了空间钢构架—钢管混凝土轴压短柱承载力的计算公式，为后续进一步研究提供技术支撑。

(a) 空间钢构架—钢管混凝土(b) 空间钢构架混凝土 (c) 钢管混凝土

图1空间钢构架—钢管混凝土柱截面形式

Fig.1Section forms of spatial steel frame concrete filled steel tube columns

1轴心受压空间钢构架—钢管混凝土柱的约束机理

轴心受压空间钢构架—钢管混凝土柱的约束机理兼有空间钢构架约束混凝土和钢管约束混凝土的双重作用特征。

1.1轴心受压钢管外空间钢构架混凝土柱的约束机理

(a) 横向核心有效约束区　　　　　　　　　　　　　 　(b)纵向核心有效约束区

1.2轴心受压内埋钢管混凝土柱的约束机理

在加载初期，若不考虑钢管和混凝土这两种材料之间的粘结作用，由于钢管与核心混凝土的变形相协调，以及没有钢管的套箍效应作用，可近似认为核心混凝土处于单向受力的状态，而钢管以纵向压应力为主。随着荷载的增加，钢管和混凝土的横向膨胀不断增大，当钢管的横向膨胀低于混凝土的横向膨胀时，核心混凝土将会受到钢管的约束作用，并随着竖向压力的增大而增大。钢管纵向压应力(σ1)不断减少，环向拉力(σ2)相应地不断增大，在钢管和核心约束混凝土之间的纵向压力将会重新分布。一方面，核心约束混凝土因受到钢管侧压力作用而处在三向受压的应力状态[图3(a)]，混凝土的抗压强度得到提高；另一方面，钢管承受的压力则减小。钢管主要承受的应力由纵向压应力转变为环向拉应力，将处于纵向受压(σ1)-环向受拉(σ2)的双向受力状态(径向压力σr=σr1-σr2，较小，可以忽略)，如图3(b)所示。

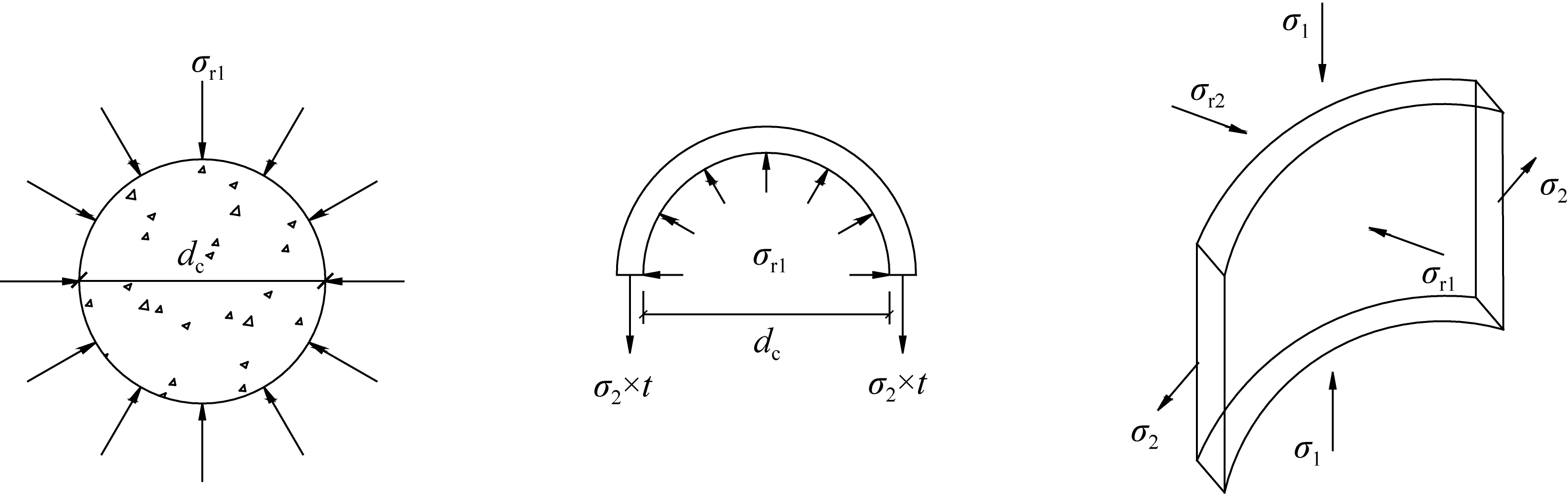
(a) 核心约束混凝土(b) 钢管

图3核心钢管混凝土柱受力模型

Fig.3Mechanical model of core steel tube concrete column

2空间钢构架—钢管混凝土短柱的轴压极限承载力计算方法

考虑空间钢构架核心约束混凝土和钢管约束混凝土的约束特征，采用叠加方法来建立空间钢构架—钢管混凝土短柱轴压承载力的计算公式。

2.1基本假定

在分析空间钢构架—钢管混凝土轴压短柱的承载能力时，遵循以下4个基本假定：

①截面应变保持平面，即空间钢构架弦杆(角钢)、钢管内外混凝土和钢管之间没有相对滑移，能够共同工作。

②不考虑混凝土的抗拉强度、收缩及徐变影响。

③不考虑空间钢构架弦杆(角钢)、钢管的局部压曲。

④不考虑柱的长细比对截面强度的影响。

根据上述基本假定和机理分析，可以将空间钢构架—钢管混凝土短柱的轴压承载力(Νu)视为内埋钢管混凝土短柱轴压承载力(Νu,stc)和钢管外空间钢构架混凝土短柱轴压承载力(Νu,ssfc)两部分叠加，即：

Νu=Νu,stc+Νu,ssfc，

(1)式中，Νu,stc为内埋钢管混凝土短柱的轴压承载力；Νu,ssfc为钢管外空间钢构架混凝土短柱的轴压承载力。

2.2内埋钢管混凝土短柱轴压承载力Νu,stc的计算

2.2.1计算假定

在计算内埋钢管混凝土短柱轴压承载力Νu,stc时，作如下假定：

①內埋钢管混凝土由钢管和钢管内核心混凝土组成，其轴向受压时的受力简图如4(a)所示。

②对于直径与壁厚之比(D/t)大于20的钢管，当承载力达到极限状态时，因其径向应力σr=σr1-σr2，远不及环向应力σ2，此时径向应力可忽略不计，钢管的应力状态可简化为沿管壁均匀分布的双向受力状态[纵向受压应力(σ1)-环向受拉应力(σ2)的应力状态]。

③钢管采用Von Mises屈服准则，即：

(2)

式中，fs为钢管钢材屈服强度，σ1和σ2分别为钢管纵向受压应力和环向受拉应力。

④钢管内核心混凝土处于三向受压状态，其侧压力与轴心抗压强度之间存在线性关系，即：

fcc1=fc+kσr1，

(3)

式中，fc为无侧压混凝土轴心抗压强度；fcc1为管内三向受压混凝土轴心抗压强度；k为系数，由试验确定；σr1为核心混凝土的侧压力。

(a) 内埋钢管混凝土轴压短柱　　　(b) 钢管外空间钢构架混凝土轴压短柱

由平衡条件(ΣY=0)[见图4(a)]可得：

Νu,stc=fcc1Acor1+σs1Aa，

(4)

式中，σs1为塑性状态时钢管的纵向压应力；Acor1、Aa分别为核心混凝土的截面面积和钢管的截面面积。

2.2.2钢管内混凝土轴心抗压强度fcc1的计算

在极限状态下可由钢管屈服应力来确定钢管核心混凝土的横向侧压力σr1。根据钢管的受力平衡条件[见图4(a)]可得：

2fst=σr1D，

(5)

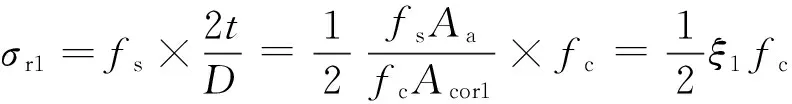
(6)

式中，ξ1为钢管混凝土的套箍指标；fs为钢管的抗拉屈服强度；Aa为钢管的横截面面积；fc为无侧压混凝土的轴心抗压强度；Acor1为钢管内的核心混凝土截面面积。

根据计算假定条件(4)，将式(6)代入式(3)可得核心混凝土的轴心抗压强度fcc1为：

(7)

2.2.3钢管进入塑性状态时纵向压应力σsl的计算

(8)

其中，负号表示为压应力。

根据钢管的受力平衡，可得：

(9)

将式(9)代入式(8)，可得：

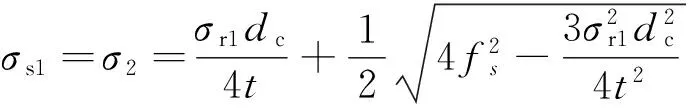
(10)

将式(7)和式(10)代入式(4)，可得内埋钢管混凝土短柱轴压承载力的计算公式为：

Νu,stc=fcAcor1+kσr1Ac+σs1Aa。

(11)

2.3钢管外空间钢构架混凝土短柱轴压承载力Νu,ssfc的计算

根据基本假定条件(3)，不考虑空间钢构架弦杆(角钢)的局部压曲，但考虑由于空间钢构架对核心混凝土的约束作用致使其抗压强度提高的影响。

由平衡条件(ΣY=0)可得：

(12)

2.3.1空间钢构架约束混凝土的有效约束系数ke的计算

考虑到纵向相邻角钢之间和横向相邻缀条之间混凝土的非约束区域，则沿纵向相邻缀条的中间高度截面上的有效约束区面积Ae为：

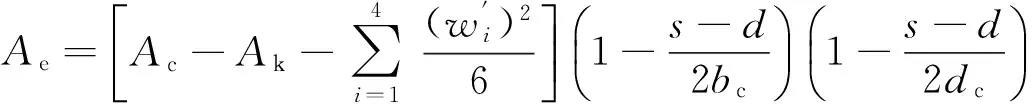
(13)

则空间钢构架对核心混凝土的有效约束系数为ke：

(14)

(15)

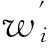
2.3.2空间钢构架约束混凝土的平均约束应力σr2的计算

图5为缀条隔离体的受力图。

(a) 截面宽度方向缀条受力的平衡简图 (b) 截面高度方向缀条受力的平衡简图

图5横向缀条隔离体受力示意

Fig.5Mechanical sketch of the isolation body about lateral lacing bar

由平衡条件可得：

2fyvAss1=(σr2·s)bc，

(16)

2fyvAss1=(σr2·s)dc，

(17)

将式(16)和式(17)相加并整理，可得空间钢构架约束混凝土的平均约束应力为：

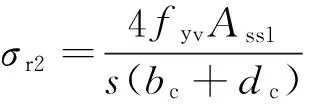
(18)

式中，fyv为横向缀条的抗拉屈服强度；Ass1为单个横向缀条的截面面积；s为横向缀条间距。

式(18)又可表达为：

(19)

空间钢构架约束混凝土短柱的套箍系数(约束指标)ξ2为：

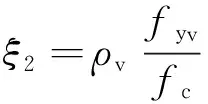
(20)

(21)

式中，ρv为横向缀条的体积配箍率，即横向缀条包围的空间钢构架约束混凝土每单位体积中的缀条的体积，按式(21)计算；Ass1为单侧缀条截面面积；fyv为缀条的抗拉屈服强度；fc为混凝土单轴抗压强度。

2.3.3钢管外空间钢构架约束混凝土的抗压强度fcc2的计算

核心约束混凝土的轴心抗压强度与侧压力之间具有线性关系，即：

(22)

(23)

将式(23)代入式(22)，可得：

fcc2=fc+keσr2，

(24)

将式(19)代入式(24)，可得：

(25)

将式(25)代入式(12)可得

(26)

2.4空间钢构架—钢管混凝土轴压短柱承载力Nu的计算

将式(11)和式(26)代入式(1)，可得空间钢构架—钢管混凝土短柱的轴压承载力计算公式为：

(27)

其中，第一项为钢管外空间钢构架混凝土短柱的轴压承载力，第二项为内埋钢管混凝土短柱的轴压承载力。

系数α和系数k分别由轴心受压空间钢构架混凝土短柱和轴心受压钢管混凝土短柱的试验确定。

①系数α

根据文献[14]中18个空间钢构架混凝土短柱试件轴心受压试验结果(Ak=0)，可确定系数α的平均值为1.588。取α=1.6，则钢管外空间钢构架混凝土短柱轴压承载力的计算公式为：

(28)

②系数k

根据文献[6]中12个钢管混凝土短柱轴心受压试验结果，可确定系数k的平均值为1.593，取k=1.6，则内埋钢管混凝土短柱轴压承载力的计算公式为：

Νu,stc=fcAcor1+1.6σr1Ac+σslAa。

(29)

③空间钢构架—钢管混凝土短柱轴压承载力的计算

由式(28)和式(29)可得空间钢构架—钢管混凝土短柱的轴压承载力公式为：

(30)

文献[15]中3个空间钢构架—钢管混凝土轴压短柱试件和文献[17]中14个空间钢构架—钢管混凝土轴压短柱有限元模拟试件的承载力计算值/试验值的平均值为0.958 9，均方差为0.039 9，离散系数为0.041 6。这表明式(30)可很好地计算空间钢构架—钢管混凝土短柱的轴压承载力。

3结语

①轴心受压空间钢构架—钢管混凝土短柱的约束机理兼有空间钢构架约束混凝土和钢管约束混凝土的双重特征，即空间钢构架对钢管外混凝土具有一定的约束作用，使钢管外混凝土处于三向受压状态，以及钢管约束的核心混凝土处于三向受压状态。空间钢构架—钢管混凝土约束效果可用空间钢构架有效约束系数与套箍系数的乘积(keξ2)和钢管混凝土的套箍指标(ξ1)来衡量。

②考虑空间钢构架约束混凝土和钢管约束混凝土的特点，采用叠加方法来建立空间钢构架—钢管混凝土短柱轴压承载力的计算公式，其计算值与试验值吻合较好，可以用作计算空间钢构架—钢管混凝土短柱的轴压承载力。

参考文献:

[1]KNOWLES R, PARK R.Axial load design strength for concrete filled steel tubes [J]. Journal of Structural Division, 2006, 92(10): 2125-2153.

[2]MANOJKUMAR V, CHITAWADAGI A, MATTUR C, et al.Axial capacity of rectangular concrete-filled steel tube columns-doe approach [J]. Construction and Building Materials, 2010, 24(12): 585-595.

[3]ELLOBODYA E, YOUNG B, LAM D.Eccentrically loaded concrete encased steel composite columns [J]. Thin-Walled Structures, 2011, 49(1): 53-65.

[4]江枣，钱稼茹.钢管混凝土短柱轴心受压承载力与钢管作用研究[J]. 建筑结构，2010，40(8)：94-98.

[5]江枣.竖向组合构件抗震性能研究[D]. 北京：清华大学，2010.

[6]李云飞.钢管混凝土轴心受压构件受力性能的试验研究[D]. 西安：西安建筑科技大学，2003.

[7]陈梦成，刘京剑，黄宏.方钢管再生混凝土轴压短柱研究[J]. 广西大学学报(自然科学版)，2014，39(4)：693-700.

[8]梅村魁，大泽胖监修.劲性钢筋混凝土结构抗震设计[M]. 北京：中国建筑工业出版社，1988:36-70.

[9]聂建国，赵洁，柏宇，等.钢管混凝土核心柱轴压极限承载力[J]. 清华大学学报(自然科学版)，2005，45(9)：1153-1156.

[10]聂建国，柏宇，李盛勇，等.钢管混凝土核心柱轴压组合性能分析[J]. 土木工程学报，2005, 38(9)：9-13.

[11]李永进，廖飞宇.钢管混凝土叠合柱偏压工作性能研究[J]. 广西大学学报(自然科学版)，2012，37(6)：1083-1088.

[12]张文福，计静，鲁华伟，等.角钢约束混凝土轴压短柱力学性能研究[J]. 建筑结构学报，2012，33(4)：121-127.

[13]王恺.空间钢构架约束混凝土的本构关系及其轴压短柱的有限元分析[D]. 苏州：苏州科技大学，2015.

[14]陈晓峰.空间钢构架混凝土柱受力性能试验研究[D]. 苏州：苏州科技大学，2015.

[15]刘建明.核心钢管外包钢骨混凝土短柱受压性能试验与理论研究[D]. 秦皇岛：燕山大学，2011.

[16]徐亚丰，王越.碳纤维钢骨-钢管混凝土柱抗震性能试验与有限元分析[J]. 沈阳建筑大学学报(自然科学版)，2013，29(4)：612-620.

[17]李伟强.双空间钢构架混凝土柱抗震性能试验研究[D]. 苏州：苏州科技大学，2016.

[18]MANDER J, PRIESTLEY M, PARK R.Observed stress-strain behavior of confined concrete [J]. Journal of the Structural Engineering, 1988, 114(8): 1827-1849.

[19]MANDER J, PRIESTLEY M, PARK R.Theoretical stress-strain model for confined concrete [J]. Journal of the Structural Engineering, 1988, 114(8): 1808-1823.

(责任编辑唐汉民裴润梅)

收稿日期：2016-03-16；

修订日期：2016-04-05

基金项目：建设部科技研究项目(99-031-2)

通讯作者：唐兴荣(1963—)，男，江苏苏州人，苏州科技大学教授，工学博士；E-mail：tangxingrong01@163.com。

doi:10.13624/j.cnki.issn.1001-7445.2016.0607

中图分类号：TU312+.3TU375.3

文献标识码：A

文章编号：1001-7445(2016)03-0607-08

Calculation of axial compressive capacity of spatial steel frame concrete filled steel tube short columns

LI Wei-qiang， TANG Xing-rong， JIA Huan

(Jiangsu Province Key Laboratory of Structure Engineering, Suzhou University of Science and Technology, Suzhou 215011, China)

Abstract：In order to study the calculation of axial compressive bearing capacity of spatial steel frame concrete filled steel tube short columns, the constraint mechanism of spatial steel frame concrete filled steel tube short columns was analyzed. On the basis of experimental study and finite element nonlinear analysis, the axial compressive capacity formula of the short columns was established by using superposition method and considering the constraint of spatial steel frame applied on concrete outside of the steel tube and the constraint of steel tube on core concrete. The calculated values coincide with the test values. The calculation formula can be used for predicting the axial compressive bearing capacity of spatial steel frame concrete filled steel tube short columns.

Key words:composite column; axial compressive bearing capacity; constrain effect; spatial steel frame concrete; concrete filled steel tube

引文格式： 李伟强，唐兴荣，贾欢.空间钢构架—钢管混凝土短柱轴压承载力计算方法[J].广西大学学报(自然科学版)，2016，41(3)：607-614.