基于霍尔元件的磁悬浮心脏泵转子径向位移检测

肖林京，李波，孙传余，文艺成，徐秀秀

(山东科技大学 机械电子工程学院，山东 青岛 266590)

人工心脏泵[1]体积小、质量轻、功耗低、悬浮稳定，成为医学工程和磁悬浮控制领域的重要课题[2]。心脏泵控制方式一般分为永磁控制、电磁控制和混合控制。永磁控制不需要控制系统，属于被动悬浮，稳定性差；电磁控制通过电磁力实现主动悬浮，控制灵活，能量消耗大；混合控制综合二者优势，在主动控制保证控制精度的前提下，由永磁偏置降低系统功耗。磁悬浮控制系统中，磁悬浮轴承转子位移检测[3]是实现精确稳定控制的关键环节。由于转子径向2个自由度偏移量之间以及径向偏移量与轴向偏移量之间在位置检测结果中均存在耦合关系，增加了径向2自由度位置检测的难度。

下文针对一种混合控制的离心式心脏泵，利用ANSOFT/Maxwell 2D软件，分析了其径向永磁轴承外部某定点处磁感应强度值与轴承内磁环偏移量间的关系特性；提出了一种基于霍尔传感器的径向2自由度位移检测方案，实现了径向位移的精确检测，完善了文献[4]未给出径向2自由度位移检测方法的不足；并通过仿真对比，证明了该方案的正确性。

1 磁悬浮心脏泵结构

离心式磁悬浮心脏泵结构如图1所示。定子绕组和转子叶轮组成双定子单转子开关磁阻电动机[5]，其中转子叶轮既作开关磁阻电动机转子导通磁路，也作转子叶轮驱动液体流动；定子绕组在轴向两侧各设有一套，且每套绕组均包括主绕组和悬浮力绕组，其中主绕组提供驱动转矩，悬浮力绕组提供转子径向调节力；左右径向永磁轴承位于轴向两侧，与开关磁阻电动机共同实现离心式心脏泵的混合磁悬浮，并通过开关磁阻电动机实现磁悬浮轴承转子的旋转驱动和径向位移调节；2个入口位于定子轴向两端，出口位于定子外壳径向外壁。

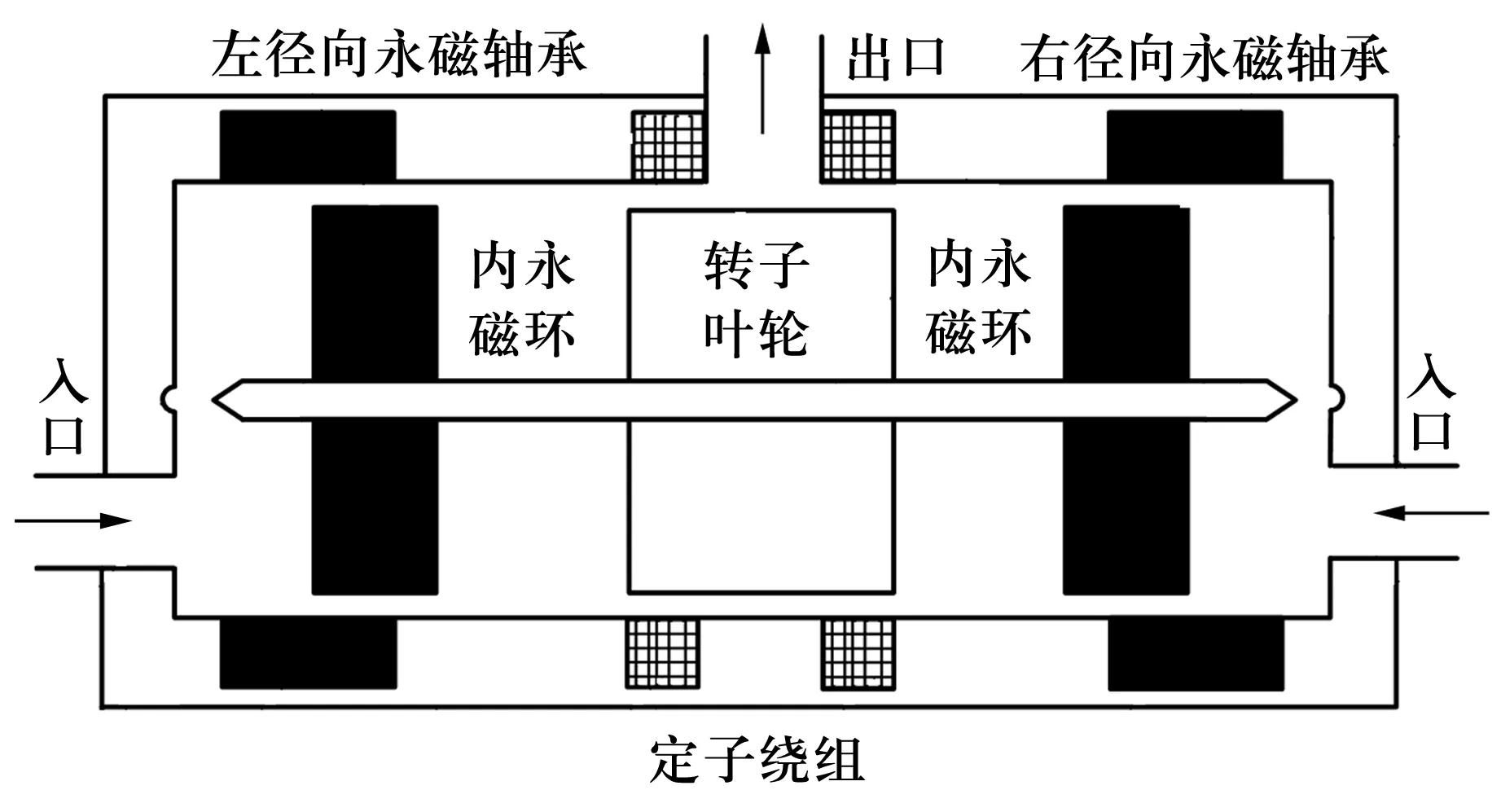
图1 人工心脏泵结构图

离心式磁悬浮心脏泵在径向永磁轴承永磁偏置作用下，完成转子径向和轴向被动悬浮，又在开关磁阻电动机悬浮力绕组的电磁力作用下，实现径向2自由度主动悬浮；由开关磁阻电动机主绕组产生电磁力，驱动转子叶轮旋转，使血液经入口流入，出口流出，实现血液驱动功能。

2 径向永磁轴承外部磁场分布特性

由心脏泵结构可知，径向永磁轴承内永磁环固定在磁悬浮轴承转子转轴两端，当转子发生偏移时，内永磁环会随之运动，导致径向永磁轴承外部空间磁场分布发生变化，可通过检测径向永磁轴承外部某点处磁感应强度变化反映转子位置变化。由于径向2自由度及轴向位移变化均会引起磁感应强度的变化，为掌握转子位移变化量与磁感应强度间的关系，首先通过有限元软件，仿真径向永磁轴承外部空间磁场变化特性，进而得到转子位移与径向永磁轴承外部某点处磁感应强度间的数学关系。

以径向永磁轴承[6-7]为仿真对象，利用ANSOFT/Maxwell2D有限元仿真软件，建立二维模型，如图2所示。径向永磁轴承内永磁环内径8 mm，外径12.5 mm，高15 mm；外永磁环内径15 mm，外径20 mm，高15 mm；内外永磁环径向同轴，且内永磁环凸出外永磁环轴向距离7.5 mm。永磁材料参数：剩磁Br=12.5 T；矫顽力Hc=947 kA/m；相对磁导率μr=1.050 4。设置内永磁环运动参量，A为磁感应强度检测点，通过瞬态模块，仿真内永磁环运动过程中A点磁感应强度随偏移量的变化，如图3～图5所示。

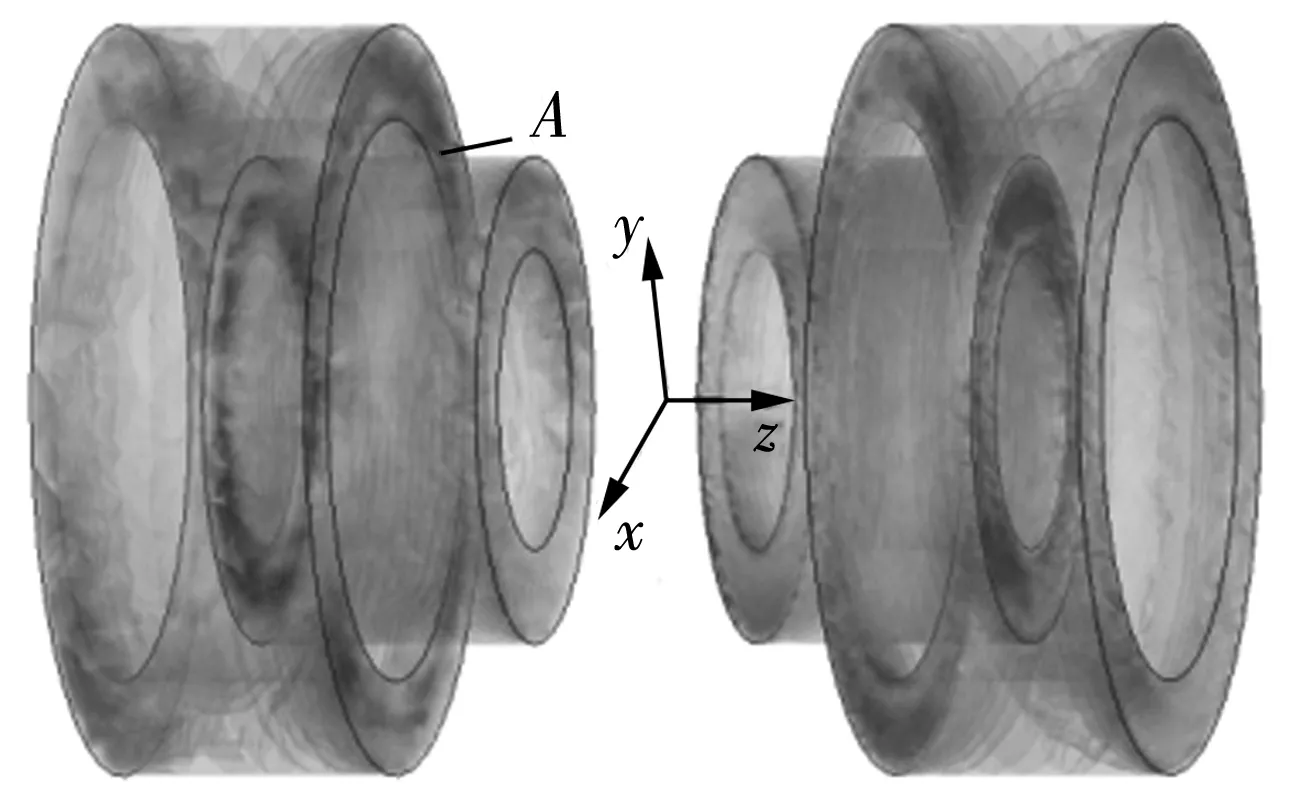
图2 径向永磁轴承仿真模型图

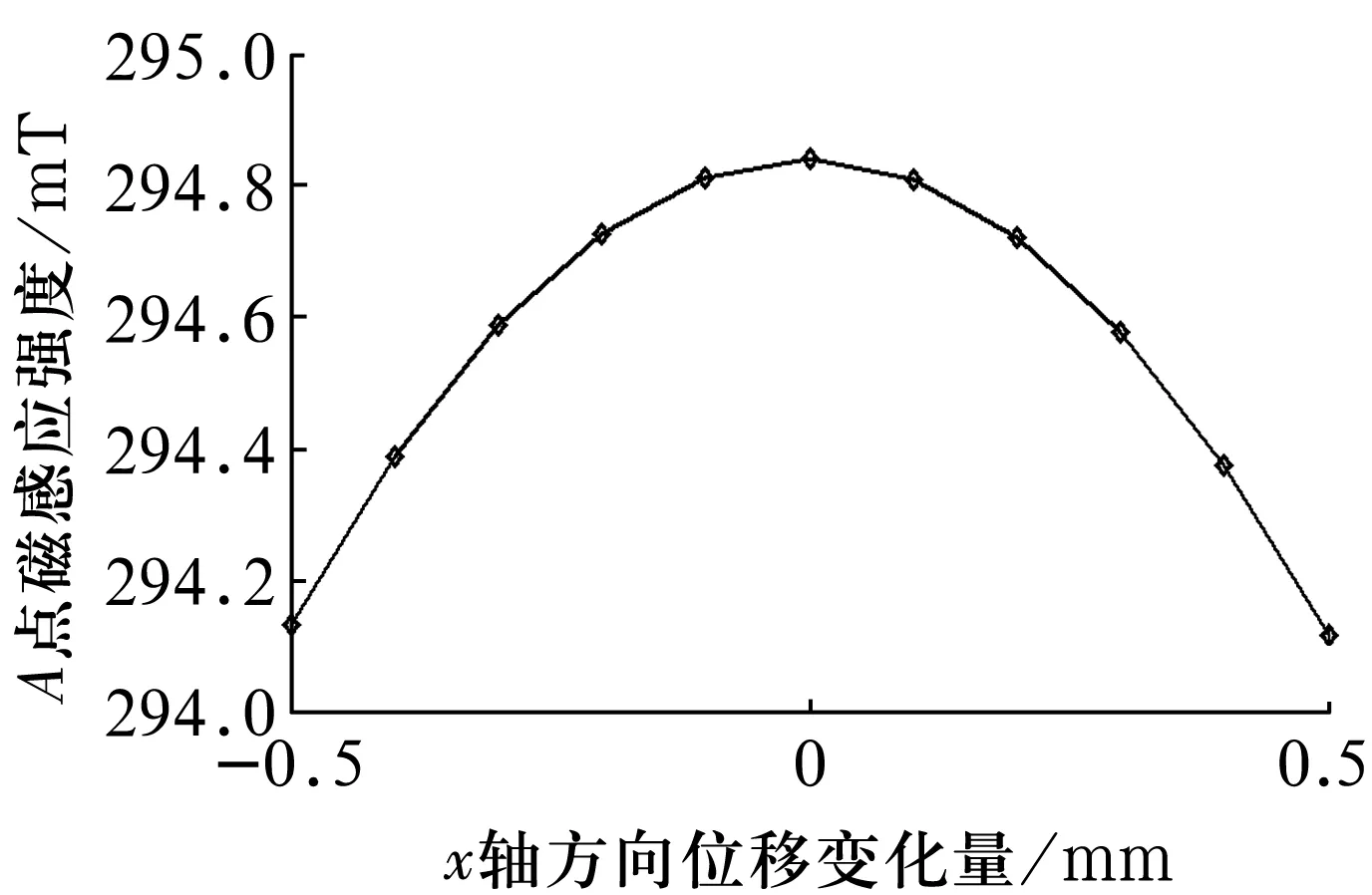
图3 x轴方向位移与A点磁感应强度关系图

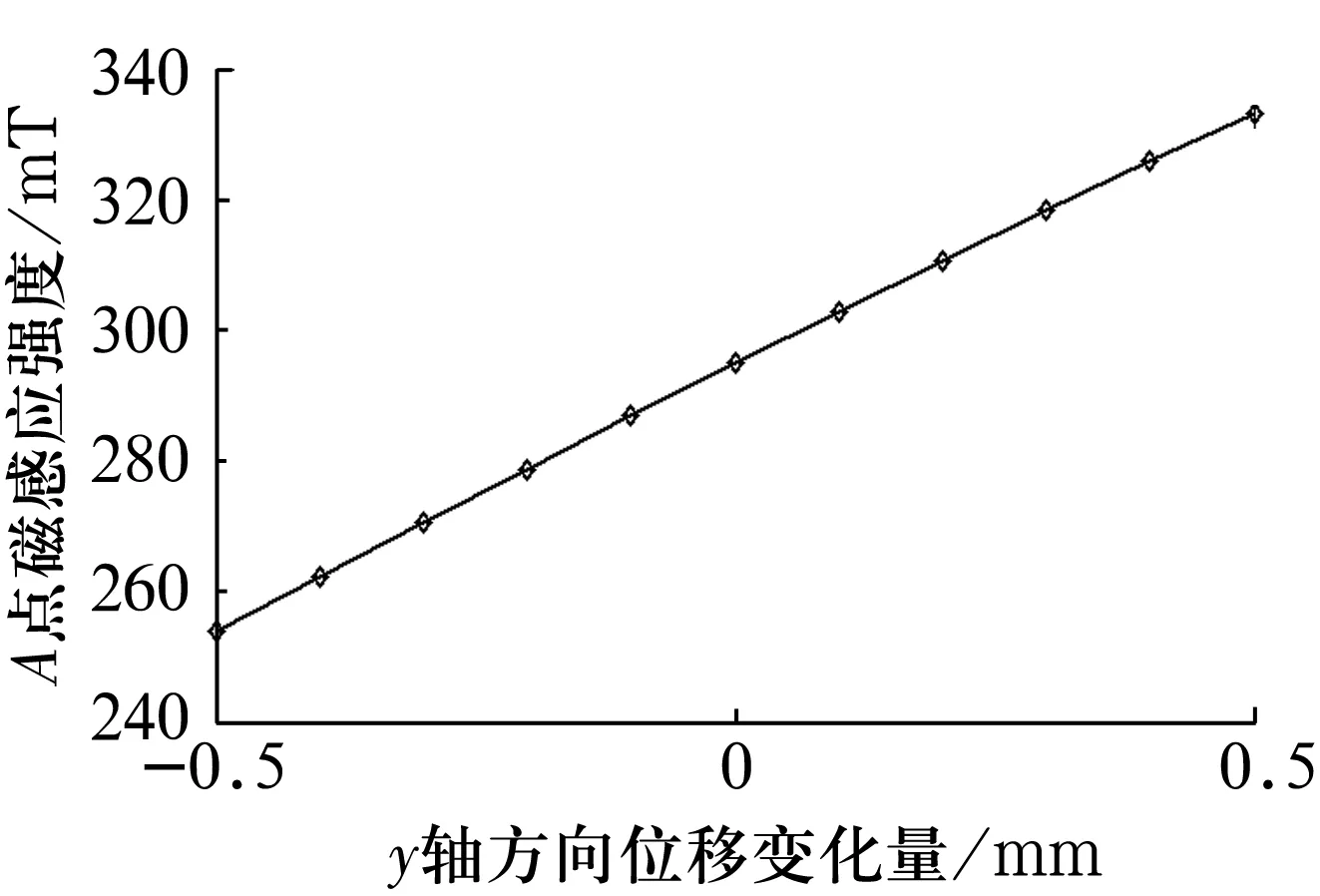
图4 y轴方向位移与A点磁感应强度关系图

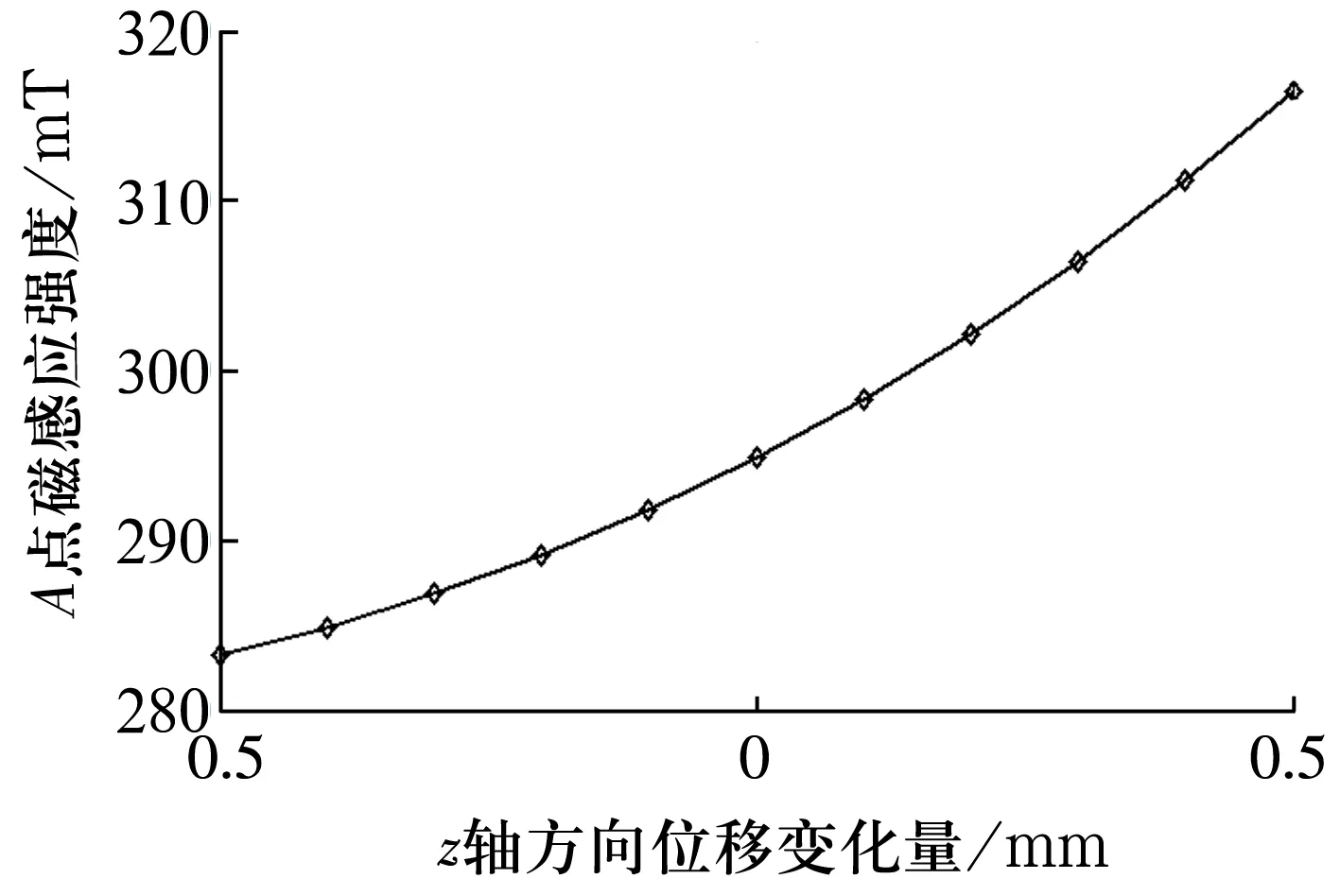
图5 z轴方向位移与A点磁感应强度关系图

由图3可知，当内永磁环沿x轴方向发生微小偏移时，A点磁感应强度为x向偏移量Δx的偶函数，且随着偏移量Δx变化，A点磁感应强度值基本保持恒定，可认为A点磁感应强度与x向偏移量Δx近似无关；由图4可知，当内永磁环沿y轴方向发生微小偏移时，A点磁感应强度随着y向偏移量Δy的增加而增加，近似呈正比例关系，经计算可得，该比例系数为79.40 T/m；由图5可知，当内永磁环沿z轴方向发生微小偏移时，A点磁感应强度随z向偏移量Δz的增加而增加，也近似呈正比例关系，比例系数为33.24 T/m，但曲线正比例效果略差于图4曲线。因此，当内永磁环处于平衡位置时，A点磁感应强度为294.84 mT，方向如图2所示。

3 径向位移计算

由于磁悬浮轴承转子的位移为微小量，根据有限元仿真结果，可认为检测点A处磁感应强度只与偏移量Δy，Δz相关，与Δx无关。

假设当转子仅在径向(y向)发生微小偏移时，认为磁感应强度BA只与Δy相关，则其与偏移量Δy可线性化为

BA=kAyΔy+BA0，

(1)

式中：BA0为转子处于平衡位置时A点磁感应强度，BA0=294.84 mT；kAy为A点磁感应强度与y向位移系数的比值。

同理，当转子仅在轴向(z向)发生微小偏移时，磁感应强度BA与偏移量Δz有

BA=kAzΔz+BA0，

(2)

式中：kAz为A点磁感应强度与z向位移系数的比值。

转子偏移运动过程中，既会发生径向位移也会发生轴向位移，因此，为描述转子位移量与A点磁感应强度BA的关系，需解决径向和轴向位移的耦合问题。

设系数kAy，kAz与偏移量Δy，Δz存在如下耦合关系[4]

(3)

式中：aAy，aAz均为系数；kAy0，kAz0均为常数，且kAy0=79.40 T/m，kAz0=33.24 T/m。

根据(1)～(3)式可得

BA=(aAy+aAz)ΔyΔz+kAy0Δy+kAz0Δz+BA0

。 (4)

选择体积小、操作简单的霍尔传感器为元件，根据霍尔效应将磁场强度B转化为霍尔电动势输出

UH=kdIB，

(5)

式中：UH为霍尔电动势；kd为霍尔元件灵敏度；I为控制电流。

将4个霍尔传感器分别置于图6中A(同图2中A点)，B，C，D点，具体布置方式如下：A与C，B与D均关于xy平面左右对称分布；A与B，C与D均关于径向永磁轴承轴线旋转对称分布，且旋转角为90°；由于霍尔元件测量时具有方向性，安装时需使霍尔传感器平面法线与检测点磁感应强度的夹角为0，以避免霍尔传感器的测量误差。

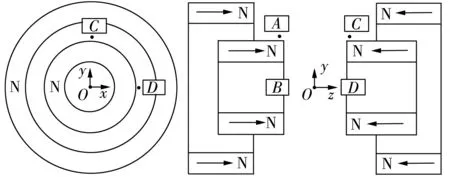
图6 霍尔传感器布置图

根据A点处磁感应强度特性的仿真结果可知，C点处磁感应强度同样仅与Δy和Δz相关。由于C与A点关于xy平面左右对称，当磁悬浮轴承转子发生位置偏移时，有

BC=-(aAy+aAz)ΔyΔz+kAy0Δy-kAz0Δz+BC0

，(6)

式中：BC为C点磁感应强度；BC0为磁悬浮轴承转子处于平衡位置时C点的磁感应强度。

A，B两点关于径向永磁轴承轴线旋转对称，且旋转角为90°，因此B点处磁感应强度仅与Δx和Δz相关，并有

(7)

式中：kBx为B点磁感应强度与x向位移系数的比值；kBz为B点磁感应强度与z向位移系数的比值；aBx，aBz均为系数；kBx0，kBz0均为常数，对比A点可知，kBx0=79.40 T/m，kBz0=33.24 T/m。

B点磁感应强度BB为

BB=(aBy+aBz)ΔxΔz+kBx0Δx+kBz0Δz+BB0

,(8)

式中：BB0为磁悬浮轴承转子处于平衡位置时B点的磁感应强度。

由于D与B点关于xy平面左右对称，当磁悬浮轴承转子发生位置偏移时，则有

BD=-(aBy+aBz)ΔxΔz+kBx0Δx-kBz0Δz+BD0

,(9)

式中：BD为D点磁感应强度；BD0为磁悬浮轴承转子处于平衡位置时D点的磁感应强度。

根据霍尔传感器布置位置可知：BA0=BB0=BC0=BD0。

联立(4)式与(6)式，(8)式与(9)式可得

(10)

式中：B0=BA0=BB0=BC0=BD0。

联立(5)式和(10)式可得

(11)

式中：UA，UB，UC，UD分别为A，B，C，D点的输出霍尔电动势；U0分别为转子处于平衡位置时4个点的输出霍尔电压。

4 仿真

径向永磁轴承仿真模型参数如前文所述，利用ANSOFT/Maxwell 2D有限元软件，通过瞬态仿真模块设定内永磁环的运动过程为：由初始位置位移量(Δx0,Δy0,Δz0)=(0.1,0.4,0.2)到终止位置位移量(Δx,Δy,Δz)=(0.4,0.6,0.5)的直线运动，进而仿真输出运动过程中A，B，C，D各检测点的磁感应强度。

已知仿真过程中，内永磁环运动路径为(0.1,0.4,0.2)→(0.4,0.6,0.5)，定义该路径为转子仿真位移；将仿真输出的A，B，C，D各点磁感应强度值带入转子位移检测模型(10)式，计算得到转子位移量，定义该位移量为模型计算位移。内永磁环运动过程中，转子仿真位移与模型计算位移的拟合效果如图7所示，虚线部分为转子仿真位移，实线部分为模型计算位移。由图可知，x，y径向2自由度均有较好的拟合效果，经计算，试验中的最大检测偏差小于5%，该转子位移检测法能准确地检测径向2自由度的位移量。

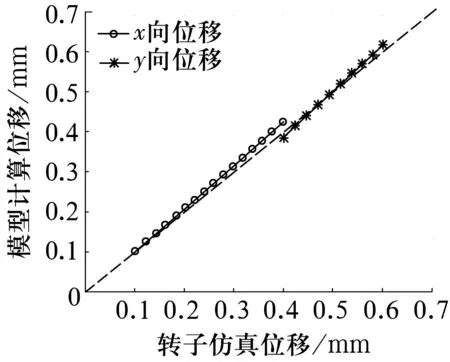
图7 模型计算位移与转子仿真位移对比

5 结束语

研究了径向永磁轴承外部某点处磁感应强度值与内永磁环微小位移量的关系特性。根据4个霍尔传感器在空间中的分布位置，给出了解耦方法，准确实现了磁悬浮轴承转子径向2自由度的位移检测，且操作简单、计算量小。人工心脏泵磁悬浮轴承转子径向位移检测研究，对实现磁悬浮轴承转子的径向稳定悬浮，具有一定的理论和工程指导意义。