角接触球轴承刚度计算与分析
2016-07-27王东峰方斌李庆荣张进华
王东峰,方斌,李庆荣,张进华
(1.洛阳轴研科技股份有限公司,河南 洛阳 471039;2.河南省高性能轴承技术重点实验室,河南 洛阳 471039;3.滚动轴承产业技术创新战略联盟,河南 洛阳 471039;4. 西安交通大学 机械工程学院,西安 710049;5.西安市铁路公安处,西安 710000)
符号说明
A——内、外沟曲率中心距
Dw——钢球直径
Dpw——球组节圆直径
E——等效弹性模量
f——沟道曲率系数
Fc——钢球离心力
Fx,Fy,Fz——外载荷在x,y,z方向的分量
Jw——钢球转动惯量
k0——椭圆率参数,接触区长半轴与短半轴之比
K——钢球与套圈的接触刚度
K0——钢球与套圈的Hertz接触常数
K′——轴承刚度
l——受载前内外沟曲率中心的距离
m——钢球质量
Mg——钢球受到的陀螺力矩
My,Mz——外载荷在y,z轴的转矩
n——轴承转速
Q——钢球与套圈的接触载荷
R——沟道半径
Rs——内沟道曲率中心轨迹的半径
x——外沟曲率中心与球心的距离
Z——钢球个数
α——接触角
φ——钢球的方位角
θ——钢球的姿态角
φ——钢球的位置角
λ——载荷分配系数
γy——y轴方向的内外圈相对角位移
γz——z轴方向的内外圈相对角位移
δ——钢球与套圈的接触变形
δx,δy,δz——x,y,z轴方向的内外圈相对位移
ω——内圈的旋转角速度
ωw1——钢球的自转角速度
ωw2——钢球的公转角速度
Δ——球心与沟道曲率中心的距离
下标
a——轴向
r——径向
e——外圈
i——内圈
k——第k个钢球
随着机床主轴特性向高速、高精度、高刚性的方向发展,主轴的动态性能在其设计过程中需加以考虑。角接触球轴承作为机床主轴的核心零部件,其性能参数对主轴整体性能的影响至关重要。通过试验确定主轴轴承性能参数的成本较高,有必要通过建立合适的数学模型,对机床主轴角接触球轴承的特性进行仿真分析。
角接触球轴承仿真计算作为典型的非线性问题引起了众多的研究[1-7],文献[1]分析了沟道接触应力和变形的关系,并建立平衡方程分析了球轴承在任意外载荷下的载荷分布;文献[2]建立了完善的球轴承拟静力学模型,并综合考虑了离心力和陀螺力矩的作用,并结合沟道控制理论建立模型;文献[3]建立了角接触球轴承动态下刚度矩阵的5自由度求解模型;文献[4]进一步介绍了动刚度矩阵的推导过程并将其应用于主轴模型。文中在上述研究的基础上,对角接触球轴承的刚度问题进行了研究。
1 轴承刚度计算
1.1 几何关系分析
将轴承看成由内圈节点和外圈节点组成的单元,其中内圈节点相对于外圈节点有5个自由度,包括3个平动自由度和2个转动自由度。
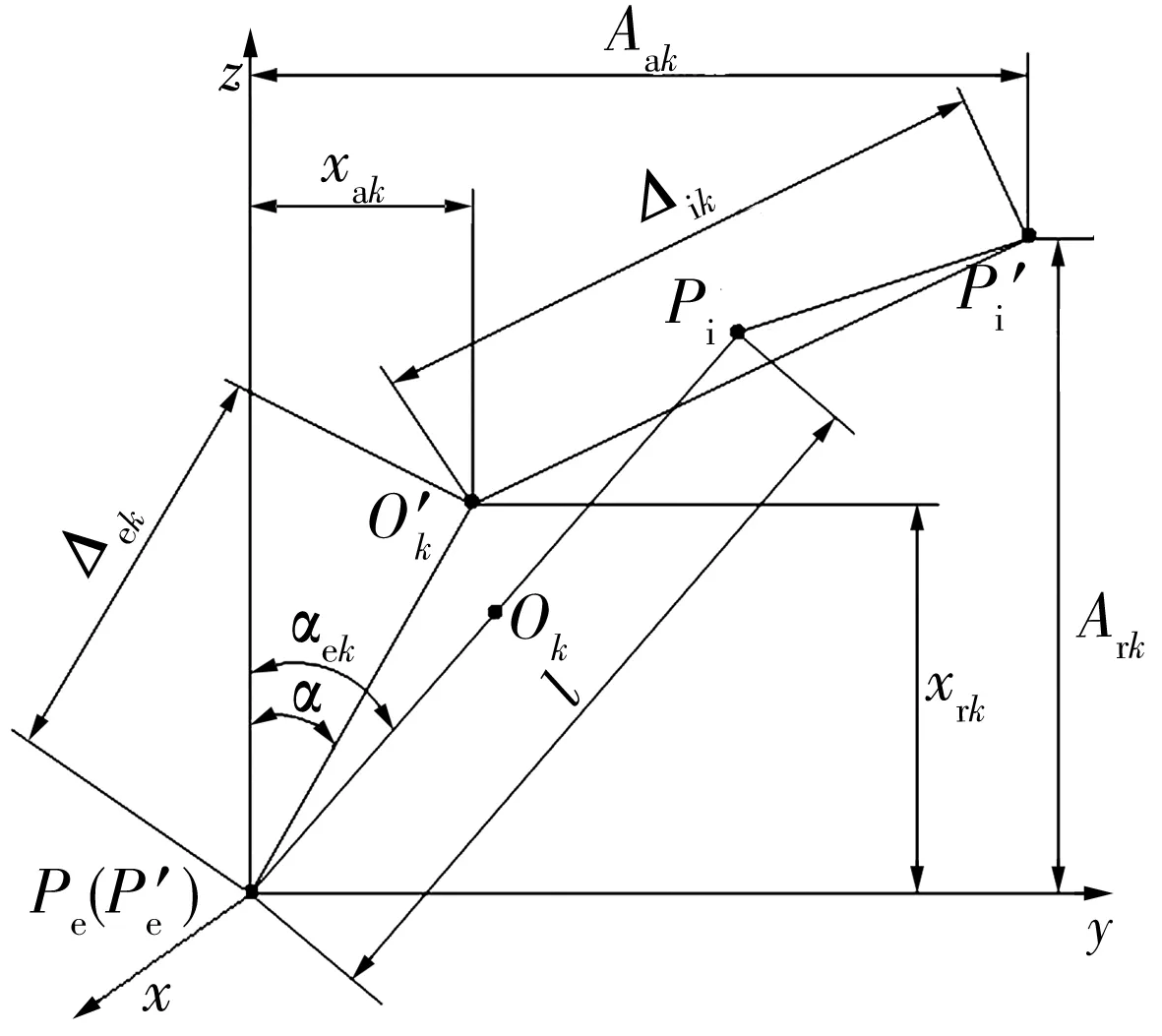
图1 受载前后钢球中心与沟曲率中心几何位置关系
由图1可知,动态条件下钢球与内外圈接触角的三角函数表达式为
(1)
Aak=lsinα+δx+γyRssinφk-γzRscosφk,
Ark=lcosα+δycosφk+δzsinφk,
l=Ri+Re-Dw=(fi+fe-1)Dw,
1.2 受力分析
1.2.1 钢球受力分析
在建立钢球的整体平衡方程之前,需要对钢球进行受力分析。为了简化分析过程,通常假设钢球在一个套圈上作纯滚动,而在另一个套圈上同时存在滚动和自旋运动,发生纯滚动的套圈通常被称为控制套圈,钢球受力情况就可以分为内圈控制理论以及外圈控制理论。钢球受力分析如图2所示,对于外圈控制理论,可认为λik=0,λek=2,而对于内圈控制理论,则有λik=λek=1。
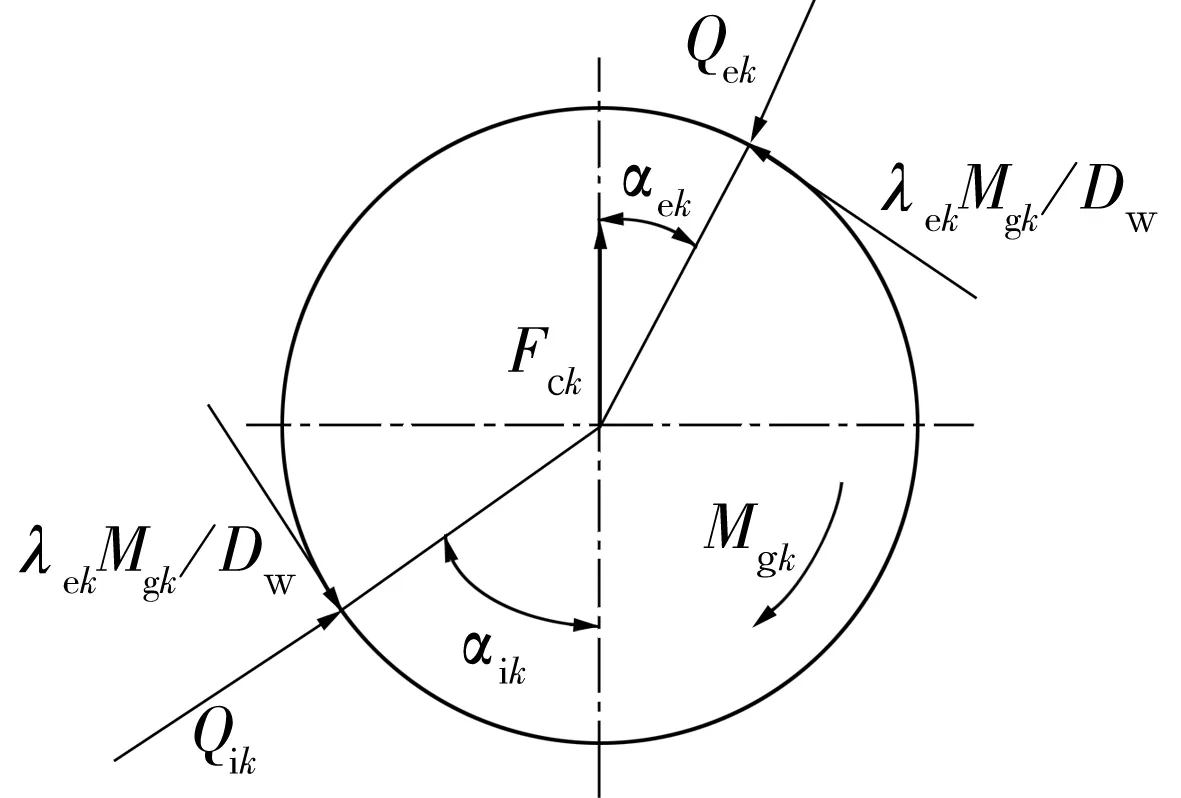
图2 钢球受力分析
由图2可得,钢球受力平衡方程为
(2)
根据Hertz接触理论,钢球与套圈的接触载荷与变形关系为
(3)
1.2.2 沟道控制准则与姿态角确定
钢球姿态角θ是钢球旋转轴与轴承轴向轴心线之间的夹角,其值与所使用沟道控制方式有关。内、外沟道控制理论的使用条件见表1[1],其中E为第2类完全椭圆积分。
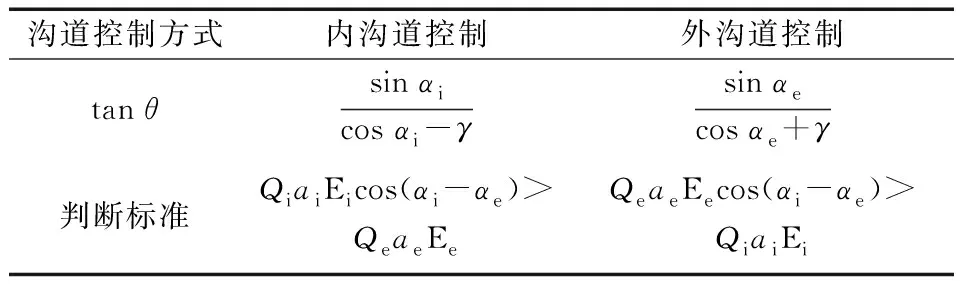
表1 沟道控制准则与钢球姿态角的确定
1.2.3 整体平衡方程
假设外力作用在内圈上,则将所有钢球与轴承内圈之间的作用力相叠加,可以得到轴承整体的受力平衡方程为
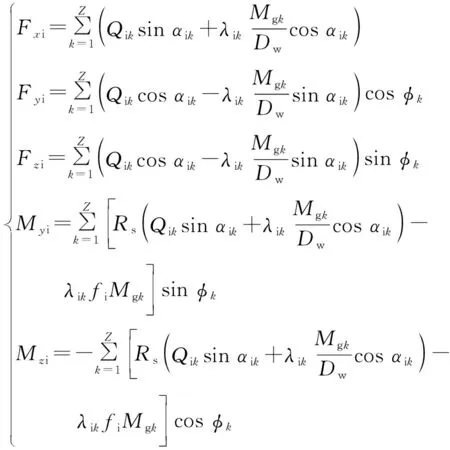
。(4)
Newton-Raphson法具有收敛速度快、通用性强等特点,故上述非线性方程组利用该方法进行求解。
1.3 轴承刚度计算
在上述角接触球轴承拟静力学模型的基础上,可以使用以下2种方法求解轴承刚度。
1)根据钢球与沟道的Hertz接触刚度间接计算轴承整体刚度,接触刚度为
(5)
式中:F为第1类椭圆积分;∑ρ为Hertz两接触体在接触点处主平面内等效曲率和。
接触刚度的轴向和径向分量为
(6)
(7)
利用所有钢球接触刚度的串并联便可得到轴承的刚度[7],即
(8)
2)将轴承所受外力F=[Fx,Fy,Fz,My,Mz]T对轴承内圈相对于轴承外圈的相对位移向量δ=[δx,δy,δz,γy,γz]T求偏导,即可以得到轴承刚度矩阵[4],其中对角线上的元素称为轴承的主刚度,也是实际工程中最为常用的轴承刚度指标。
(9)
K中的任意元素Kij(i,j=1,2,3,4,5)通过文献[4]求得。
方法1求解速率快,但高速时计算精度差,不能用于精确求解高速轴承刚度;方法2虽然求解效率一般,但求解精度高。故文中选用第2种方法进行求解。
2 计算结果及分析
2.1 静刚度计算
以7008C轴承为例进行静刚度计算,其结构参数见表2。
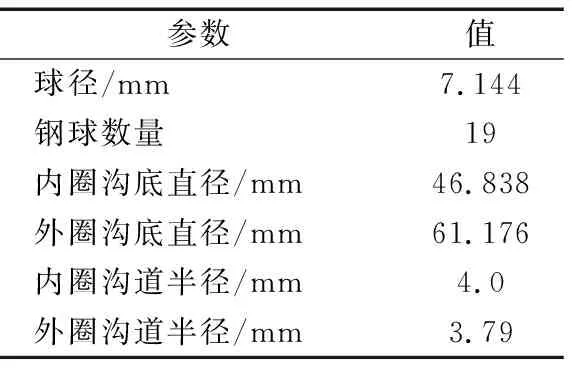
表2 轴承结构参数
对不同预紧力下的静刚度求解并进行多项式拟合,可得轴承静刚度随预紧力的变化曲线如图3所示。
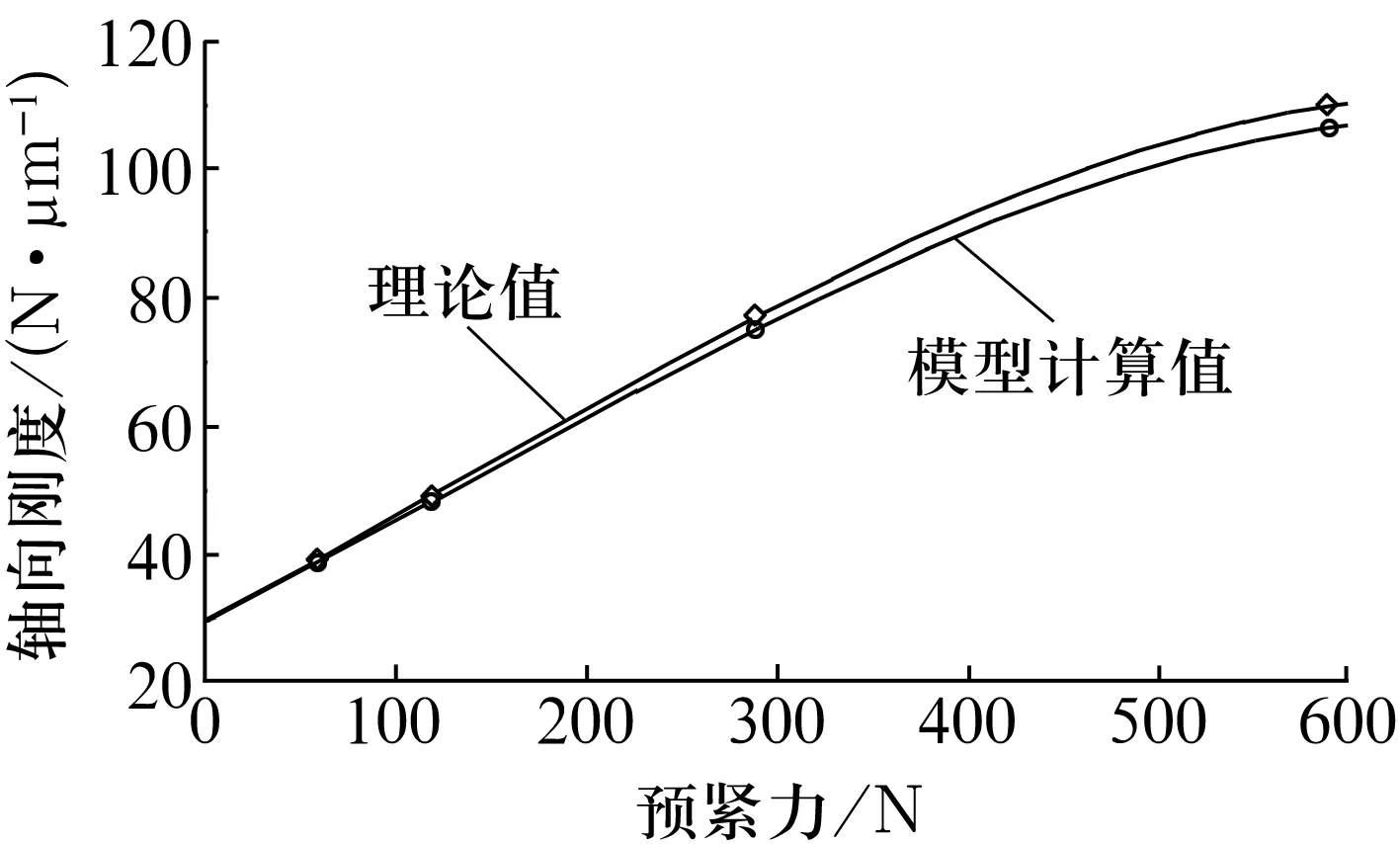
图3 轴向刚度-预紧力曲线
从图3可以看出,轴承刚度随预紧力的增大而增大,其刚度求解结果略小于理论值,相对误差在5%以下,说明静态刚度求解较为准确。同理可得,在中预紧下,轴承静刚度随径向外载荷变化曲线如图4所示,由图可以看出,随着径向载荷增大,轴承的轴向刚度减小,而径向刚度增大,且径向刚度增大趋势比轴向静刚度减小趋势更为明显。
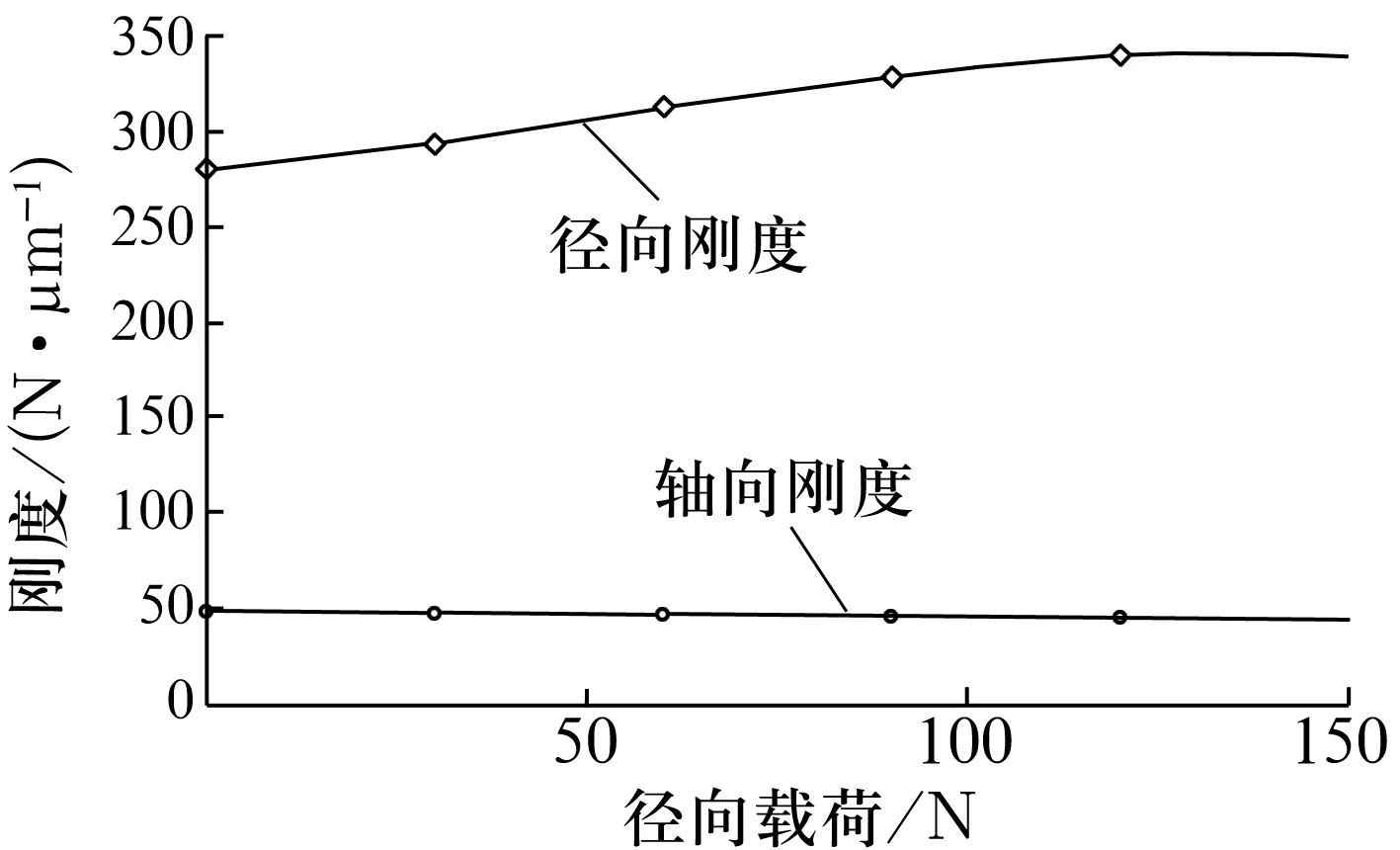
图4 120 N预紧力下静刚度-径向载荷曲线
2.2 动刚度计算
7008C在轻中重预紧力下刚度-转速及轴向位移-转速曲线如图5所示。
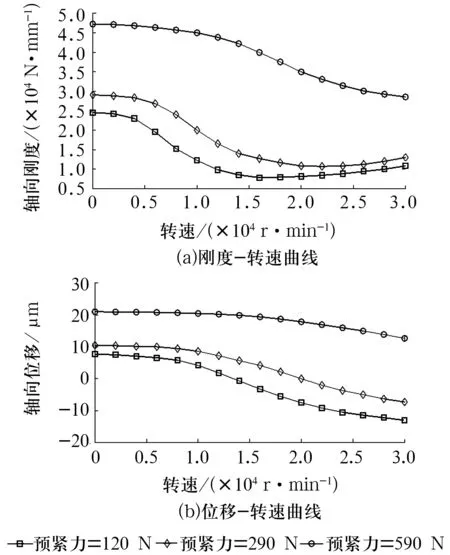
图5 不同预紧力下轴承刚度、位移与转速的关系
由图5可知,轴承动刚度随转速的增大而减小,即出现了刚度软化现象。轴承的轴向位移随转速增大也减小,这是因为随着转速的增大,内外圈在钢球离心力的作用下有远离的趋势。此外轴向刚度和轴向位移两者随转速的变化规律有一定的相似性。10 000 r/min下7008C轴承y,z方向上的径向刚度随外载荷的变化曲线如图6所示,随y方向上径向载荷的增大,轴承y方向上的径向刚度随之增大,z方向上的径向刚度减小。
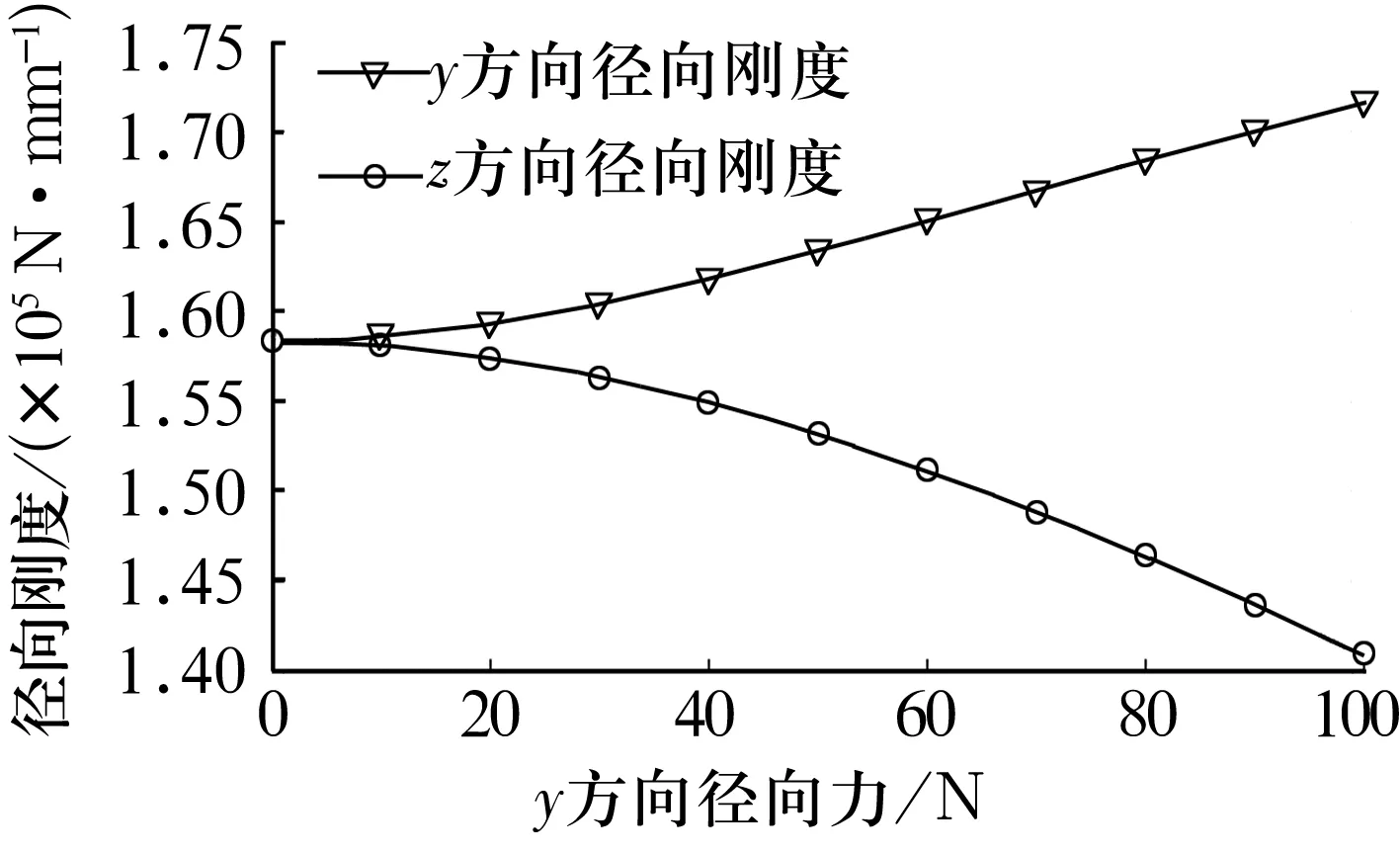
图6 y,z方向上的径向刚度随y方向径向载荷的变化曲线(n=10 000 r/min)
计算结果表明,预紧力和转速是轴承刚度最重要的2个影响因素,因此将三者放在一起研究,7008C轴承预紧力-转速-刚度及轴承预紧力-转速-轴向位移的拟合曲面关系如图7所示,即可以通过其中任意2个参数来确定第3个参数。实际工作中往往通过工作刚度和工作转速来确定所需要的初始预紧力,从而对特定工况下轴承初始预紧力的选择给出一定的推荐数值。
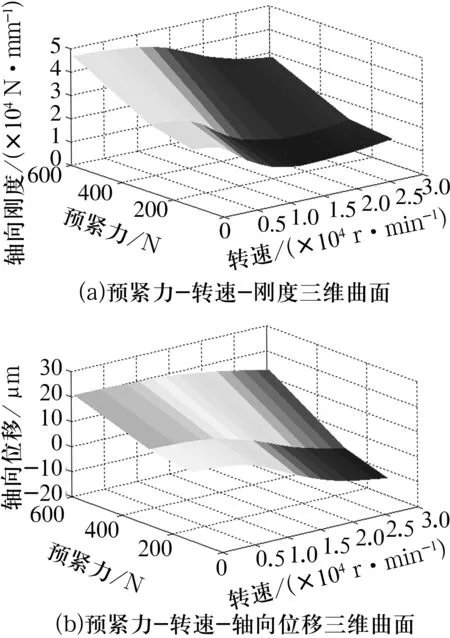
图7 轴承预紧力、转速与刚度、轴向位移的关系图
3 结论
1)所提出的轴承刚度计算方法是可行的。
2)轴承静刚度随着预紧力的增大而增大。
3)在相同预紧力作用下,随着径向载荷的增大,轴向静刚度减小,而径向静刚度逐渐增大,且径向静刚度增大趋势较轴向静刚度减小趋势更为明显。
4)轴承动刚度随着转速的增大会发生刚度软化现象,预紧力越大,软化点越高,且其刚度的变化与轴向位移的变化具有相似性。
