变载荷条件下的滚动轴承在线故障诊断方法
2016-07-26蒋丽英李茜茜崔建国席剑辉
蒋丽英,李茜茜,崔建国,席剑辉
(沈阳航空航天大学 自动化学院, 沈阳 110136)
机械设备运转过程中载荷、转速的变化以及设备故障产生的冲击、摩擦等因素均会导致滚动轴承振动信号具有非平稳性[1]。经验模态分解(Empirical Mode Decomposition,EMD)[2-5]和小波分析[6-8]是近年来广受瞩目的非平稳信号处理技术。EMD虽然是一种自适应信号处理方法,但计算量大,且本征模式分量的总数、频率及计算时间都具有不确定性,响应时间上难以满足在线实时诊断的要求;小波分析存在的突出问题是目前尚无有效方法解决最优小波基的选择,并且其计算量随分解层次的增加而增加;在线处理非平稳信号时,以上2种方法在线计算量太大,难以满足在线故障诊断对实时性的要求。
Fisher判别式分析(Fisher Discriminant Analysis,FDA)是一种降低特征空间维数的线性模式分类方法,被广泛地应用于模式识别和故障诊断[9-10]等领域。由于滚动轴承结构对称,载荷区间位置固定,其振动信号的非平稳性表现为周期平稳性;因此,结合动态主分量分析的思想,提出了一种带时延窗口动态FDA(DFDA)的在线故障诊断方法。
DFDA通过引入时延窗口的方式捕获滚动轴承振动信号的周期平稳性,即由当前时刻和前d个时刻振动信号所构成的增广向量作为故障特征向量,并根据已知故障的历史数据建立FDA故障诊断模型。为了使滚动轴承在线故障诊断具有鲁棒性,即在一定载荷参数摄动下故障诊断系统仍具有较好的诊断性能,选取不同载荷条件下的试验数据对DFDA的有效性进行了验证。
1 Fisher判别式分析
FDA的基本思想是按照最大化类间离散度、同时最小化类内离散度的准则,寻找一个从高维向低维空间映射的线性变换矩阵,从而获得最佳判别矢量空间(FDA空间),使故障模式在该空间内有最佳的可分离特性。
1.1 FDA的基本原理
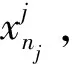
(1)
同理,将p种已知故障类的样本数据矩阵按列的方向依次放入一个新的矩阵中,则获得构成一个n行m列的总体样本数据矩阵X,即
X=[(X1)T(X2)T… (Xp)T]T,
(2)
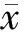
(3)
(4)
(5)
St=Sw+Sb,
其中,Sj为第j类的类内离散度矩阵,即
(6)
在非小样本情况下,求解最优FDA向量问题可归结为如下问题,即
Sbwj=λjSwwj;j=1,2,…,p-1,
(7)
式中:wj为第j个FDA向量。将p-1个FDA向量按特征值λj从大到小排列成新矩阵Wp,即
(8)
Wp∈m×(p-1)为判别权矩阵,亦称为FDA模型。因此,通过判别权矩阵Wp,数据从原始m维空间投影到p-1维判别空间,实现了不同类别数据的最优分离。其线性变换关系可表示为
(9)
其中:zi∈(p-1)×1,称为判别得分向量。
1.2 低维FDA空间的确定
尽管经过FDA变换后可得到较低维的判别空间,但当FDA应用到独立于训练数据集的新数据时,为了降低分类或诊断方法的误诊断率,必须进行降维处理。AIC(Akaike Information Criterion)是一种仅依赖于训练集信息的最优阶次确定方法,故采用AIC计算降维的最优阶次α,其可由AIC的最小值确定,即
(10)
式中:f(α)为将数据投影到前α个FDA向量得到的训练集的误诊断率。经过降维后确定一个最优判别权矩阵Wα,从而将原始数据投影到故障诊断空间,在此空间内实现故障模式的分类。
1.3 动态FDA
DFDA采用时延窗口引入时滞数据,分析变量间的时序相关特性,从而捕获滚动轴承振动信号的周期平稳性。因此,包含当前测量变量和前d个采样时刻测量变量的增广变量向量为
xd(k)=[xT(k)xT(k-1) …xT(k-d)]T,
(11)

,(12)
(13)
DFDA就是对具有时滞信息的Xd进行特征值分解,获取最优判别权矩阵。
2 基于DFDA的滚动轴承在线故障诊断方法
2.1 离线建模阶段
离线建模阶段的主要任务是根据所获取的历史振动信号建立DFDA模型。其具体步骤为:
1) 收集各种已知故障的历史振动信号。假设包含p种不同故障类型(包括正常轴承)振动信号的一维时间序列为xj(j=1,2,…,p),据此建立数据集。
2) 确定时延窗口d的大小,构建总体建模样本数据集Xd。首先,提取每类振动信号的瞬时能量。在第k采样时刻,第j类振动信号的瞬时能量ej(k)定义为
ej(k)=|xj(k)|,
(14)
则包含前d个时刻的能量特征向量Ej(k)为
Ej(k)=[ej(k)ej(k-1)…ej(k-d)]T,
(15)
最后,根据(12)和(13)式,构建维数为n×(d+1)总体数据样本集Xd。

2.2 在线应用
在线故障诊断阶段就是利用已经离线建好的DFDA模型实时分析滚动轴承的运行状态。在线故障诊断过程的步骤如下:
1) 在线采集滚动轴承的振动信号x(k)(第k个采样时刻的振动信号),提取当前瞬时能量e(k)。根据 (15) 式构建具有时延信息的能量特征向量Enew(k)=[e(k)e(k-1)…e(k-d)]T。

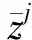
最小的欧式距离所对应的故障类别即是最终的故障决策。
4) 重复以上步骤,分析下一个采样时刻滚动轴承的状态。
3 应用实例与分析
3.1 振动信号采集及试验设计
本试验采用美国西储大学轴承数据中心所提供的SKF6205-2RS型滚动轴承试验数据[12]进行分析,采样频率为12 kHz,故障轴承的损伤直径为0.178 8 mm,深度为0.279 4 mm。通过对健康轴承(HB)、滚动体故障轴承(BF)、内圈故障轴承(IRF)以及外圈故障轴承(ORF)分别在4种载荷条件下运行的试验数据进行分析,以验证所提出的在线故障诊断方法在变载荷条件下的有效性和鲁棒性。其中,0%载荷条件下的试验数据用于建立DFDA模型,每种故障样本长度为4 800点;用50%(0.74 kW),100%(1.47 kW)和150%(2.21 kW)负载条件下的数据作为测试样本。在0%负载条件下,4种轴承状态的振动信号如图1所示。
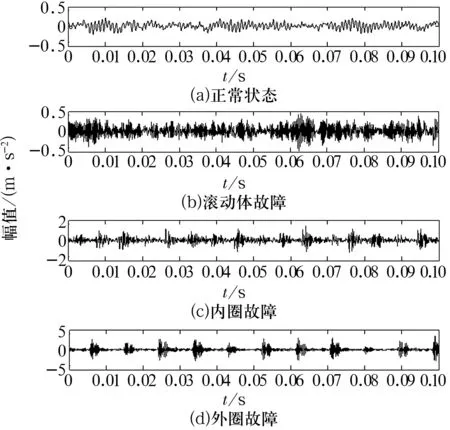
图1 0%负载条件下4种轴承状态的振动信号
3.2 时延窗口对故障诊断性能的影响
选取几种不同大小的时延窗口,分别建立带有时滞信息的DFDA模型,并对比分析建模样本数据在各自的最佳判别空间内的可分离性,各建模样本在判别空间的投影如图2所示。
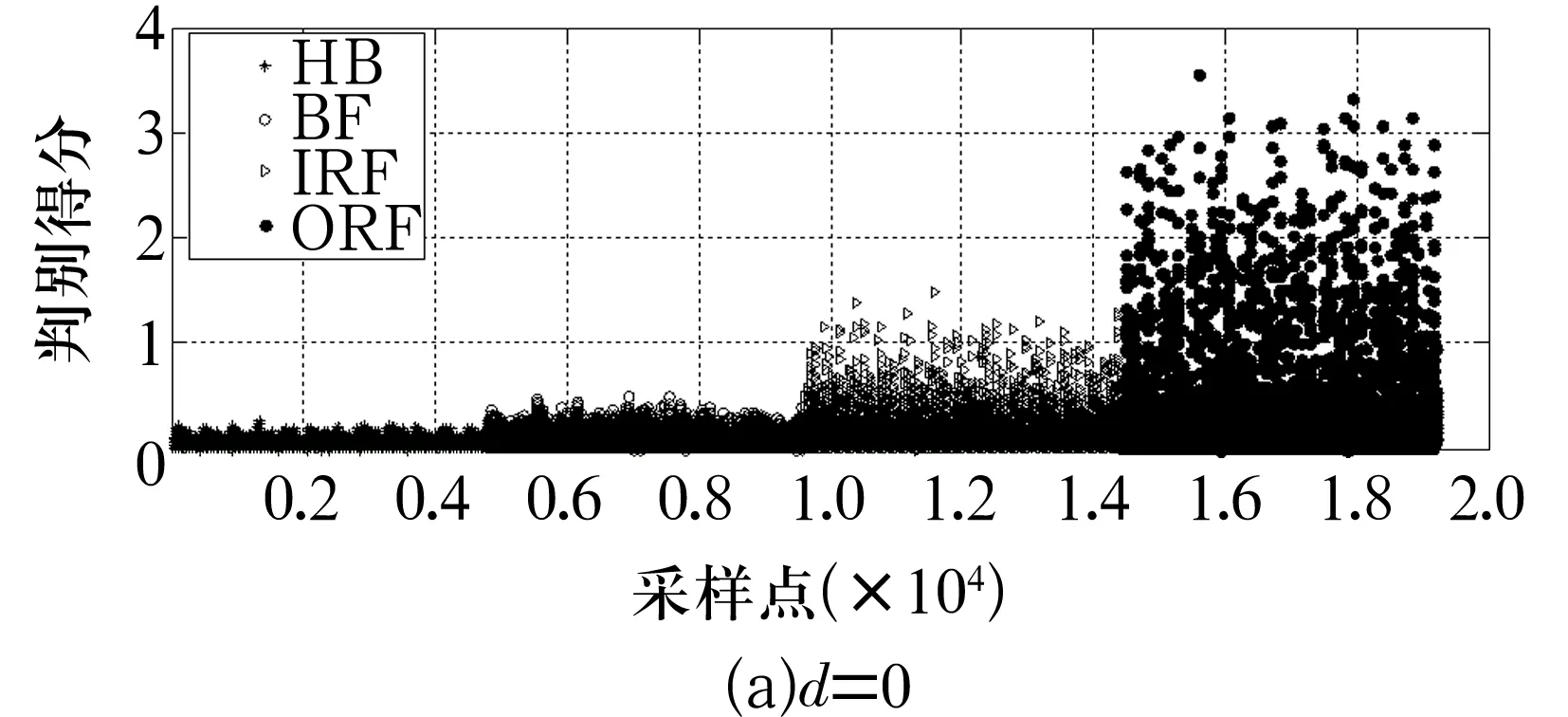
图2 建模样本在判别空间的投影
从图2中可以看出:
当d取0时,建模数据中不包含过程任何动态信息,所建的DFDA模型退化为传统的FDA模型,经FDA分析后得到了一个一维的最佳判别空间,但4种故障类型的可分性在该空间内非常差。
当d增至100时,得到一个三维的判别空间(没有降维),图中的坐标分别代表运用最优判别权矩阵将原始数据投影到故障诊断空间后获得的新的特征。由图可知4种故障彼此之间仍存在交集。
当d=250时,得到了一个二维最佳判别空间。滚动体故障、内圈故障、外圈故障三者之间的样本数据在此判别空间已完全分离,但正常轴承与滚动体故障仍有少量样本存在交集。
当d分别取500和600时,都得到了一个一维的最佳判别空间,且样本数据在这2个空间中能够被完全分离。只是d=600时各类间的距离比d=500时的略大,故障类间的分离度略有增加。但随着d继续增加,故障分离度的增加并不明显。因此,可将500作为参考设定值对延时窗口d进行设置。
另外,采用欧氏距离作为故障模式分类的判别准则,应用不同时延窗口的DFDA模型时,样本数据故障正确识别率见表1。
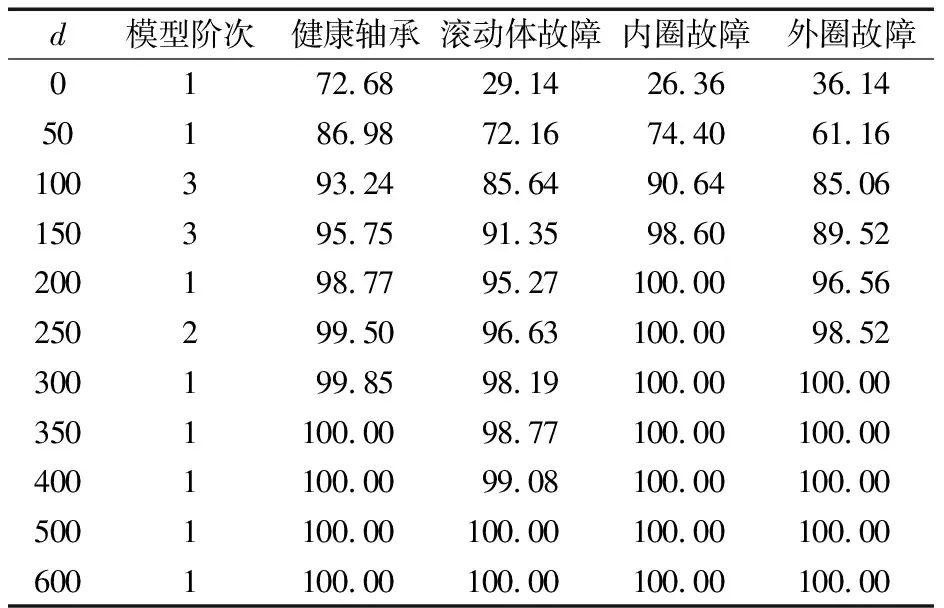
表1 不同时延窗口建模样本的故障正确识别率
试验结果表明:随着时延窗口的增大,DFDA模型包含的时滞信息越多,故障类间的离散度也随之增大,故障的可识别性提高,故障诊断的正确识别率也随之增加。当时延窗口增至500时,所有故障样本的正确识别率可达到100%。
3.3 变载荷条件下故障诊断性能比较与分析
为进一步分析上述故障诊断方法在变载荷条件下故障诊断能力,分别选用12 000个连续采样的加速度信号(1 s所采集的振动信号)作为测试样本集,在变载荷条件下运用d=300,500和600时所建立的DFDA模型进行故障诊断,结果见表2。
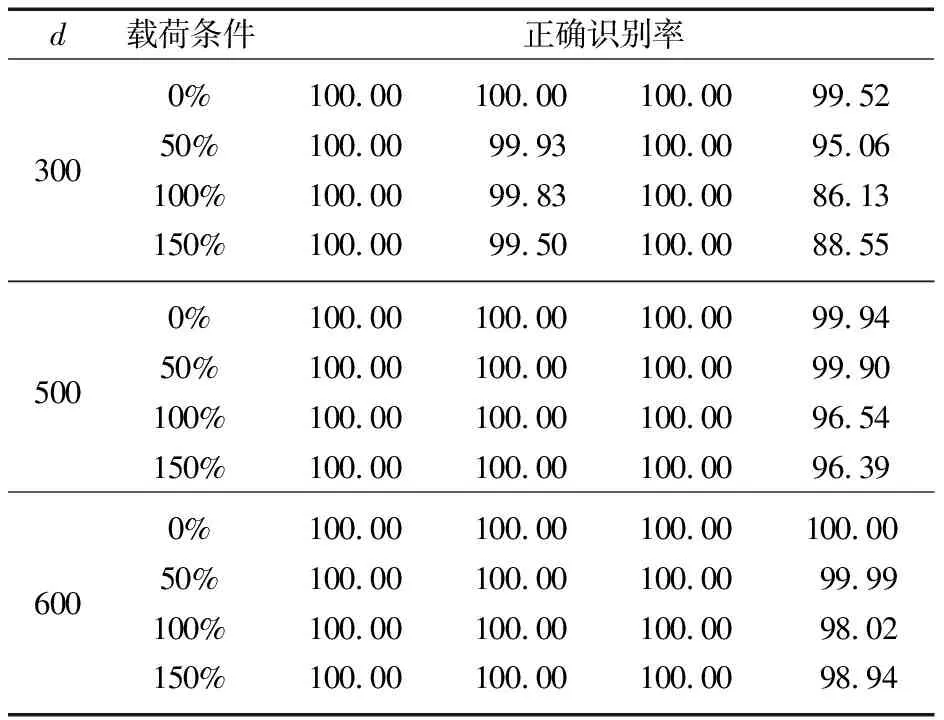
表2 不同载荷条件下故障正确识别率
由表2可知,载荷的变化对外圈故障诊断精度的影响较大,但随着时延窗口的增加,外圈故障的识别率也随之增加;而其他3种故障在不同时延窗口及载荷条件下的识别率均达到了100%。因此,通过设置合适的时延窗口,DFDA模型对变载荷条件的变化具有很强的鲁棒性,且具有很高的诊断精度。
3.4 算法的实时性分析
仿真试验运行环境为主频2.8 GHz的计算机,仿真软件为MATLAB7.1。在上述仿真环境下DFDA模型完成1次故障决策所需的时间见表3。

表3 不同时延窗口时的平均故障决策时间
由表3可知,尽管完成1次故障决策所需要的计算时间随着时延窗口的增加而增加,但其计算时间均小于振动信号的采样时间(8.333 3×10-5s)。因此,DFDA故障诊断模型的在线计算量小、诊断精度高,可以满足在线故障诊断对实时性的要求。
4 结束语
通过引入时延窗口,DFDA故障诊断模型包含了滚动轴承运行的历史信息,无需借助其他非平稳信号处理方法就可以有效地处理具有周期平稳特性的振动信号,解决了变载荷条件下滚动轴承故障诊断的问题,而高精度的故障诊断结果也证明了该方法的有效性以及鲁棒性。
在线故障诊断时仅需调用离线建立的模型信息,在线计算量小,实时性高,更有利于实现实际工程中滚动轴承的在线故障诊断。另外,DFDA仅需当前采样时刻及前d个采样时刻的振动信号,即可实现每一采样点的轴承运行状态在线分析和诊断,有利于尽早发现故障,为维修决策争取宝贵时间。
