滚动轴承性能保持可靠性预测

夏新涛，叶亮，孙立明，常振，邱明

(1. 河南科技大学 机电工程学院，河南 洛阳 471003；2. 洛阳轴研科技股份有限公司，河南 洛阳 471039)

滚动轴承性能保持可靠性，是指在试验和服役期间，滚动轴承运行可以保持最佳性能状态的可能性，通常用函数表示，函数的具体取值称为性能保持可靠度。

性能保持相对可靠度用于表征未来时间滚动轴承运行保持最佳性能状态的失效程度。评估时间区间处于滚动轴承运行性能最佳时期，是指该时间区间内的滚动轴承运行性能状态最佳。滚动轴承运行性能最佳时期内，滚动轴承运行保持最佳性能状态是指几乎没有性能失效的可能性，该时期通常位于滚动轴承跑合期结束后邻近的时间区间。滚动轴承保持最佳性能状态运行是机械系统实现最佳性能状态运行的基础，其可靠性一旦发生变化，将会影响机械系统的安全可靠运行。因此，研究滚动轴承性能保持可靠性具有重要的学术价值和应用价值。

现有的性能可靠性预测方法一般是假设样本概率密度函数及性能失效阈值已知，从而获取性能可靠性。例如，文献[1]将轴承摩擦力矩的平稳性因数、稳定性因数作为重要参数，假设摩擦力矩的概率密度函数为正态分布函数，从而分离出变异数据及其发展趋势；文献[2]基于Weibull分布和人工神经网络，对轴承剩余寿命进行精确预测；文献[3]提出自助加权范数法，对三参数Weibull分布可靠性的最优置信区间进行评估；文献[4]在性能可靠性评估方法的基础上，提出了基于退化轨迹和基于性能退化量分布的可靠性评估方法，从而对高可靠长寿命产品进行可靠性评估。假设性能退化轨迹为时间的线性函数，认为性能服从正态分布且给定阈值，可以进行宇航系统性能退化的可靠性评估。文献[5]把灰自助原理融入泊松过程，提出灰自助泊松方法，以预测滚动轴承性能可靠性的变异过程。但该方法需要进行性能试验来获取性能阈值，试验条件不同，所对应的阈值也不同，在性能密度函数先验信息未知且没有事先设定性能阈值时，无法对滚动轴承性能可靠性的变异过程进行预测，而且，在滚动轴承服役期间，很多性能失效概率分布信息是未知的。例如，文献[6]针对轴承振动性能概率分布未知的乏信息问题，建立滚动轴承质量数据序列真值融合模型；文献[7]认为轴承摩擦力矩具有不确定的波动和趋势变化，基于最大熵原理，建立航天轴承摩擦力矩的概率密度函数。

以下在小样本无任何先验信息条件下，提出滚动轴承性能保持可靠性的评估模型，通过试验验证在概率密度函数的先验信息未知且未事先设定性能阈值的条件下，该模型预测滚动轴承性能保持可靠性的准确性。运用该模型可以在滚动轴承最佳性能状态失效的可能性变大之前采取干预措施，对滚动轴承进行维护或更换，避免发生严重的安全事故。

1 数学模型

基于自助再抽样原理、最大熵原理和泊松过程，建立滚动轴承性能保持可靠性评估的数学模型。

1.1 自助法原理

在滚动轴承运行保持最佳性能状态时期，通过试验获得一组性能数据序列X

X=(x1,x2,…,xk,…,xn)；k=1,2,3,…,n，

(1)

式中：xk为第k个性能数据；n为性能数据的个数。

从数据序列X中等概率可放回地抽样，每次抽取w个数据，得到一个样本Xb；连续重复抽取B次，可以得到B个自助样本

Xb=[xb(1),xb(2),…,xb(l),…,xb(w)] ；

b=1,2,…,B，

(2)

式中：Xb为第b个自助样本；l为生成自助样本的数据序号，l=1,2,…,w；xb(l)为第b个自助样本的第l个数据。

(3)

样本容量为B的新自助样本XBootstrap为

XBootstrap=(X1,X2,…,Xb,…,XB) 。

(4)

1.2 基于最大熵原理求解概率密度函数

根据最大熵原理，用自助样本XBootstrap中的数据构建性能样本的概率密度函数f(x)为

(5)

式中：i为原点矩阶次；m为最高原点矩阶次；c0为首个拉格朗日乘子；ci为第i+1个拉格朗日乘子。

c0应满足

(6)

式中：S为性能随机变量x的可行域，S=[S1,S2]；S1为可行域的下界值；S2为可行域的上界值。

其他m个拉格朗日乘子应满足

i=1,2,…,m。

(7)

1.3 基于小概率事件原理计算置信度

选取置信度估计值Pq分别为1，0.999，0.99，0.95，0.9，0.85，0.8，用分位数方法求出对应于Pq的第q个性能随机变量置信区间[XLq，XUq]，下界值XLq应满足

(8)

上界值XUq应满足

(9)

记录B个性能数据中落在性能随机变量置信区间[XLq，XUq]之外的个数nq，基于泊松计数方法，获得性能数据落在性能随机变量置信区间之外的频率λq为

(10)

在滚动轴承运行性能处于最佳时期获得B个性能数据之后暂停试验，取出轴承，在其滚道的滚动表面构建并模拟出性能失效时的故障，对有模拟性能失效时故障的滚动轴承进行检测，获得性能失效时的B个性能失效数据。

记录B个性能失效数据中落在性能随机变量置信区间[XLq，XUq]之外的个数vq，基于泊松计数方法，获得性能失效数据落在置信区间之外的频率βq为

(11)

性能失效时的滚动轴承性能保持相对可靠度dq为

(12)

从7个dq值中挑出小于且最靠近-10%的，将其下标q标为q*，对应的置信度估计值Pq*就是以小概率事件原理为依据，事先通过性能试验确定的置信度P。

1.4 随机变量的置信区间求解

假设显著性水平为α，α∈[0,1]，则置信水平P条件下的α为

α=(1-P)×100%。

(13)

设置信水平P条件下的性能随机变量置信区间为[XL，XU]，下界值XL应满足

(14)

上界值XU应满足

(15)

1.5 基于泊松方法求解性能保持可靠度

性能数据落在 [XL，XU]之外的频率λ为

(16)

式中：n′为性能数据落在性能随机变量置信区间[XL，XU]之外的个数。

滚动轴承性能保持可靠度R(t)用于表征时间为t时，滚动轴承运行可以保持最佳性能状态的可能性，即

R(t)=exp(-λt);t=1，2，3…n。

(17)

根据测量理论的相对误差概念，获取滚动轴承在未来时间的性能保持相对可靠度d(t)，其用于表征未来时间t时滚动轴承运行保持最佳性能状态的失效程度

(18)

式中：R(1)为当前时间t=1时滚动轴承性能保持可靠度；R(t)为未来时间t时滚动轴承性能保持可靠度。

1.6 最佳性能状态失效程度预测

滚动轴承运行性能分级的基本原理如下：

1) 根据显著性假设检验原理，若滚动轴承性能保持相对可靠度不小于0%，表示所预测的未来时间的滚动轴承性能保持可靠度不低于当前时间的滚动轴承性能保持可靠度，不能拒绝滚动轴承运行性能已经达到最佳状态；否则，可以拒绝滚动轴承运行性能已经达到最佳状态；

2) 当滚动轴承性能保持相对可靠度小于0%时，根据测量理论，相对误差绝对值在(0%，5%]之间时测量值相对于真值的误差很小；相对误差绝对值在(5%，10%]之间时测量值相对于真值的误差逐渐变大；相对误差绝对值大于10%时测量值相对于真值的误差变大。

以上述显著性假设检验原理和测量理论为依据，将滚动轴承运行性能分为S1，S2，S3，S4共4个级别：

S1：滚动轴承性能保持相对可靠度d(t)≥0%，即在未来时间t时滚动轴承的运行性能达到最佳，最佳性能状态几乎没有失效的可能性；

S2：滚动轴承性能保持相对可靠度d(t)∈[-5%，0%)，即在未来时间t时滚动轴承的运行性能正常，最佳性能状态失效的可能性小；

S3：滚动轴承性能保持相对可靠度d(t)∈[-10%，-5%)，即在未来时间t时滚动轴承的运行性能逐渐变差，最佳性能状态失效的可能性逐渐增大；

S4：滚动轴承性能保持相对可靠度d(t)<-10%，即在未来时间t时滚动轴承的运行性能变差，最佳性能状态失效的可能性增大。

根据滚动轴承运行性能的4个等级，预测滚动轴承最佳性能状态失效程度的时间历程。滚动轴承性能保持相对可靠度实际上是相对于当前时间的最佳性能状态在未来时间滚动轴承性能保持可靠度的衰减程度。负值表示衰减，即该时刻滚动轴承性能保持可靠度低于当前时间滚动轴承性能保持可靠度；正值表示不衰减。滚动轴承性能保持相对可靠度d(t)越小，滚动轴承运行性能越差，最佳性能状态失效的可能性越大。

对应于滚动轴承性能保持相对可靠度d(t)=-10%的未来时间t，是滚动轴承性能变差的临界时间，在该临界时间之前采取措施，可以避免发生因滚动轴承最佳性能状态失效引起的严重安全事故。

2 试验分析

2.1 滚动轴承最佳摩擦力矩性能状态失效程度预测

对B7000轴承进行摩擦力矩寿命试验。试验设备由真空试验装置、SS1798直流稳压电源、G1-150A高真空设备和反作用飞轮控制箱组成。在温度为20～25 ℃、相对湿度为55%以上的受控清洁且无振动的地基上进行测量，在真空罩内模拟实际工作情况。采用间接测量摩擦力矩的方法，将微型轴承摩擦力矩的测量转变为对电流的测量。反作用飞轮控制箱输出指令电压，使真空试验装置中的飞轮转动，飞轮轮体内装有检测反馈装置，该装置取样并转换后，将得到的电流信号反馈给飞轮控制箱。真空检测装置实时检测装置内的真空度，真空度低于要求便会自行启动。G1-150A高真空设备将试验装置内的空气压力抽到规定范围(理论上0.1 Pa左右，试验中控制在1 Pa左右)。轮体内的轴承摩擦发热引起功率损失，该损失随着摩擦力矩的变化而变化，使得反馈的电流也发生变化。利用观察反馈得到的电流变化间接得到轴承摩擦力矩的变化，为数据采集带来方便。数据采集的时间间隔是12 h，即每天记录2次数据。

在滚动轴承运行性能最佳时期，通过测量系统定期测量滚动轴承摩擦力矩性能，获得的原始数据序列为X=(236，232，238，235，240，242，243，248，250，250，250，248，236)。

用自助法每次抽取13个数据，共抽取20 000次，所得数据如图1所示。

图1 自助法抽取摩擦力矩数据图

运用最大熵原理，计算可得各个拉格朗日乘子为[c0，c1，c2，c3，c4，c5]=[-2.563 2，0.082 431，-0.065 891，-0.032 924，-0.139 28，0.011 61]。

由 (5) 式计算概率密度估计真值函数f(x)，概率密度分布函数如图2所示。

图2 摩擦力矩样本密度函数曲线图

选取置信度估计值P1=1，用分位数方法分别求出7个性能随机变量置信区间的上、下限值，见表1。

表1 摩擦力矩随机变量置信区间的上下限值

20 000个摩擦力矩数据中落在7个置信区间外的个数nq分别为0，7，181，925，1 749，2 719，3 779。

根据泊松计数原理，可得摩擦力矩数据落在7个置信区间外的频率λq分别为[λ1，λ2，λ3，λ4，λ5，λ6，λ7]=[0，0.000 35，0.009 05，0.046 25，0.087 45，0.135 85，0.188 95]。

考虑到滚动轴承摩擦力矩性能失效的模拟过程较困难，因此，可将λq当做λ代入(17)式，再根据(18)式可以得到不同置信水平下的摩擦力矩性能保持相对可靠度，如图3所示。为了视图方便，只取置信度估计值Pq=0.999，0.99，0.95，0.9，t=2～13年性能失效时的滚动轴承性能保持相对可靠度dq。

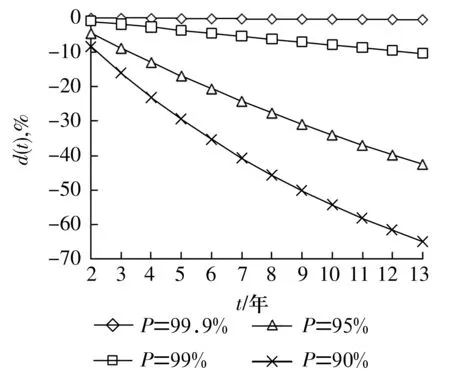
图3 不同置信水平下的摩擦力矩性能保持相对可靠度

从中挑出小于且最靠近-10%的，即P=99%=0.99时所对应的曲线，将其下标q标为q*，对应的置信度估计值为Pq*，就是以小概率事件原理为依据，事先通过性能试验确定的置信度。

由(17)式和(18)式可得未来时间t时滚动轴承运行保持最佳摩擦力矩性能状态的失效程度，即摩擦力矩性能保持相对可靠度，如图4所示。

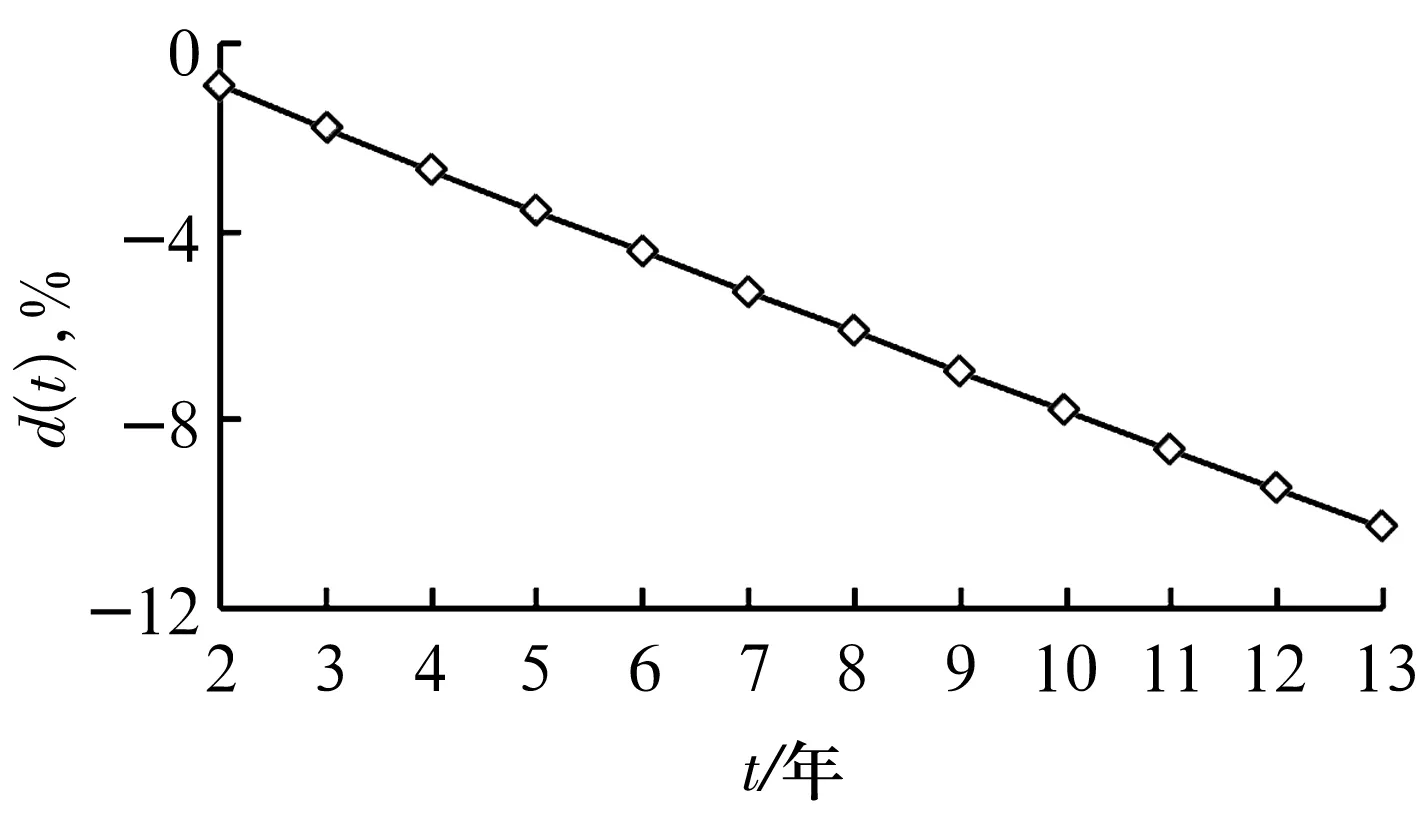
图4 摩擦力矩性能保持相对可靠度

由图4可知，当t=6时，d(t)=-4.43%∈[-5%，0%)，d(t)值接近-5%；

当t=7时，d(t)=-5.29%∈[-10%，-5%)，d(t)已经小于-5%；

当t=12时，d(t)=-9.47%∈[-10%，-5%)，d(t)值接近-10%；

当t=13时，d(t)=-10.29%<-10%，d(t)值已经小于-10%。

据此可以预测，第6 年之前，该滚动轴承的运行性能正常，摩擦力矩最佳性能状态失效的可能性小；第7 年到第12 年之间，该滚动轴承的运行性能逐渐变差，摩擦力矩最佳性能状态失效的可能性逐渐增大；到第13 年，该滚动轴承的运行性能变差，摩擦力矩最佳性能状态失效的可能性增大。

根据上述分析，在第12 年末，应当采取干预措施，对该滚动轴承进行维护或更换，避免发生因轴承摩擦力矩最佳性能状态失效带来的严重安全事故。

2.2 滚动轴承最佳振动性能状态失效程度预测

试验数据来自美国Case Western Reserve University的轴承数据中心网站的专用滚动轴承故障模拟试验台。该试验台包括一个2马力的电动机，一个扭矩传感器/译码器和一个功率测试计等。待测轴承支承电动机的转轴，驱动端轴承型号为SKF6205，风扇端轴承型号为SKF6203。用加速度传感器测量轴承振动加速度信号。驱动端转速为1 797 r/min，采样频率为12 kHz，得到轴承内圈沟道有损伤的故障数据，损伤直径分别为0.177 8，0.533 4，0.711 2 mm，损伤直径为0 mm时获得的振动加速度即为振动性能处于最佳时期的加速度原始数据。根据GB/T 24607—2009《滚动轴承 寿命及可靠性试验规程》，球轴承剥落面积不小于0.5 mm2，从而可认为磨斑直径为0.798 mm时获得的加速度数据即为振动性能处于失效时期的原始数据。

对一套SKF6205轴承进行振动寿命试验，在滚动轴承运行性能最佳时期，通过测量系统获得轴承振动加速度原始数据如图5所示。

图5 振动加速度原始数据图

用自助法每次抽取1 600个数据，共抽取20 000次，所得大样本数据如图6所示。

基于最大熵法计算可得拉格朗日乘子[c0，c1，c2，c3，c4，c5]=[4.489 58，-0.048 036 4，-0.240 004，-0.032 449 2，-0.062 889 4，0.003 081 76]。

图6 自助法抽取振动加速度数据图

由 (5) 式可计算出概率密度估计真值函数f(x)，概率密度分布函数如图7所示。

选取置信度估计值P1=1，用分位数方法分别求出7个性能随机变量置信区间的上、下限值，见表2。

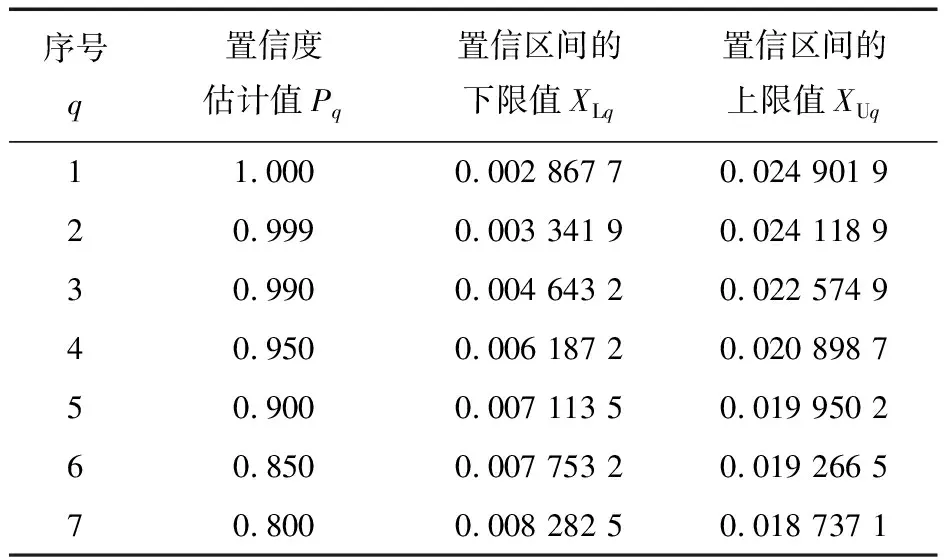
表2 振动加速度随机变量置信区间的上下限值

20 000个运行性能最佳时期的振动加速度数据落在7个置信区间外的个数nq分别为0，66，308，971，2 144，3 092，4 054。

根据泊松计数原理，可得运行性能最佳时期的磨斑直径数据落在7个置信区间外的频率λq分别为[λ1,λ2,λ3,λ4,λ5,λ6,λ7]=[0, 0.003 3,0.015 4,0.048 55,0.107 2,0.154 6,0.202 7]。

根据损伤直径为0，0.177 8，0.533 4，0.711 2 mm时获得的振动加速度数据，用蒙特卡罗方法仿真磨斑直径为0.798 mm时的1 600个振动加速度数据(仿真时间单位假设为n)。

用自助法每次抽取1 600个数据，共抽取20 000次，所得数据如图8所示。

图8 性能失效数据图

20 000个性能失效数据落在7个性能随机变量置信区间[XLq，XUq]之外的个数分别为1 610，2 105，3 503，5 484，6 832，7 855，8 750。

根据泊松计数原理，可得性能失效数据落在7个置信区间外的频率βq分别为[β1,β2,β3,β4,β5,β6,β7]=[ 0.080 5，0.105 25，0.175 15，0.274 2，0.341 7，0.392 75，0.437 5]。

由(12)式可得7个置信水平条件下，滚动轴承性能保持相对可靠度dq分别为[d1,d2,d3,d4,d5,d6,d7]=[-7.73%，-9.88%，-15.789%，-20.21%，-20.87%，-21.19%，-21.93%]。

从中挑出小于且最靠近-10%的，即P=99%=0.99时的曲线，将其下标q标为q*，所对应的置信度估计值Pq*就是以小概率事件原理为依据，事先通过性能试验确定的置信度。

对应的λ=λ3=0.015 4，由(17)式和(18)式可得未来时间t时滚动轴承运行保持最佳振动性能状态的失效程度，即振动性能保持相对可靠度，如图9所示。

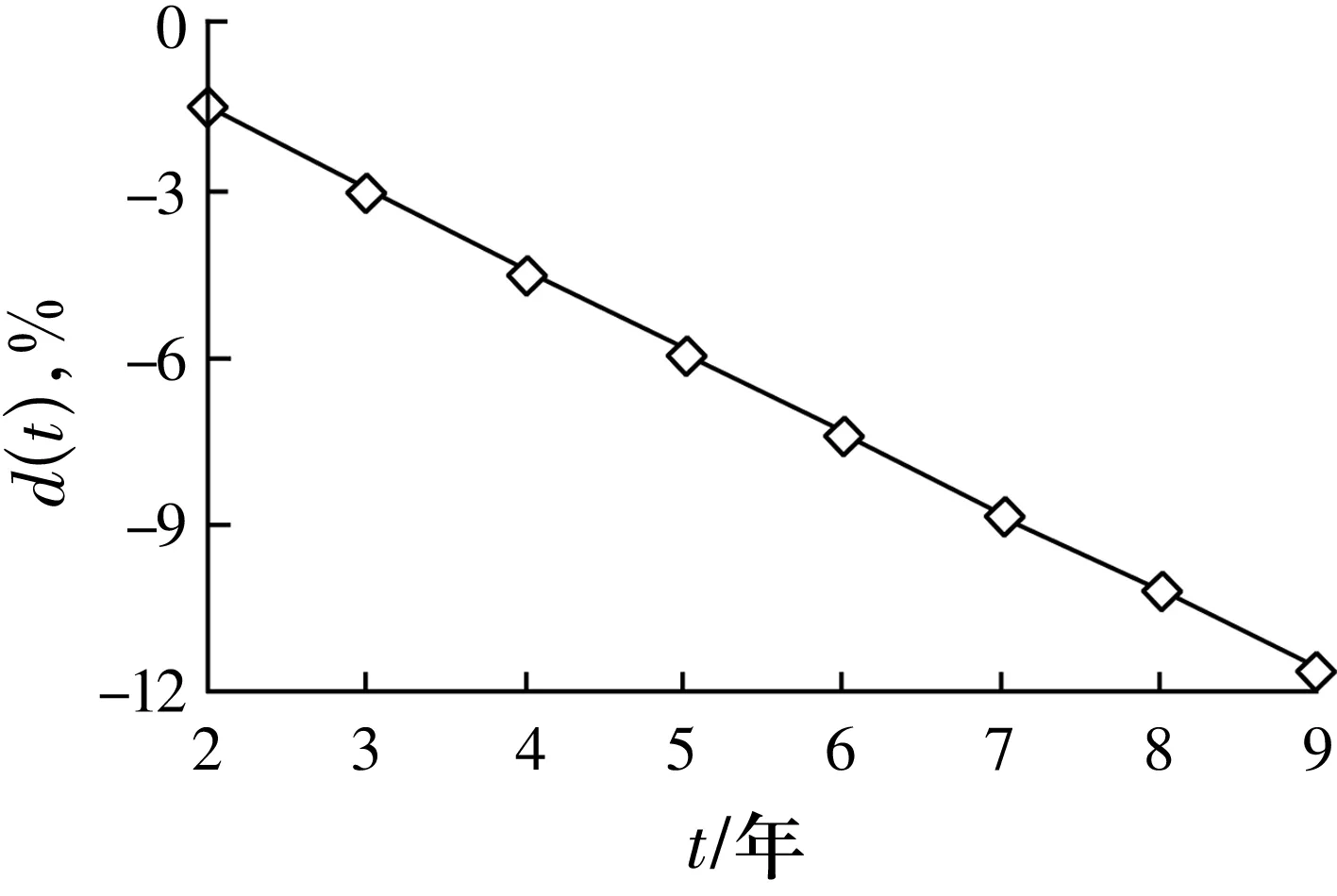
图9 滚动轴承的振动性能保持相对可靠度

由图9可知，当t=4时，d(t)=-4.51%∈[-5%，0%)，d(t)值接近-5%；

当t=5时，d(t)=-5.97%∈[-10%，-5%)，d(t)已经小于-5%；

当t=7时，d(t)=-8.83%∈[-10%，-5%)，d(t)值接近-10%；

当t=8时，d(t)=-10.21%<-10%，d(t)值已经小于-10%。

据此可以预测，第4 年之前，该滚动轴承的运行性能正常，振动最佳性能状态失效的可能性小；第5 年到第7 年之间，该滚动轴承的运行性能逐渐变差，振动最佳性能状态失效的可能性逐渐增大；到第 8 年，该滚动轴承的运行性能变差，振动最佳性能状态失效的可能性增大。

根据上述分析，在第7 年末，应当采取干预措施，对该滚动轴承进行维护或更换，避免发生因轴承振动最佳性能状态失效带来的严重安全事故。

3 结束语

提出滚动轴承性能保持可靠性的新概念，基于最大熵原理，建立性能保持可靠性评估模型。通过试验证明，该模型可以计算滚动轴承在未来时间的摩擦力矩和振动性能保持的相对可靠度，从而预测滚动轴承保持最佳摩擦力矩和振动性能状态的失效程度。该可靠性评估模型无需样本概率密度函数的任何先验信息，也无需事先设定一个置信度值。运用该模型可以在滚动轴承最佳性能状态失效的可能性变大之前采取干预措施，对滚动轴承进行维护或更换，避免发生严重的安全事故。