基于声发射波形流信号的滑动轴承故障特征双谱分析

张颖，樊瑞筱，丛蕊，张盛瑀，杨云飞

(1.东北石油大学，黑龙江 大庆 163318；2.中国石油大庆炼化公司，黑龙江 大庆 163000)

滑动轴承出现故障时，在摩擦和碰撞过程中将产生弹性应力波，可以用声发射技术进行检测[1-3]。与普通振动信号相比，声发射信号频率范围更宽，信息量更大；利用其高频段信号进行故障诊断，可以有效地抑制其他低频干扰信号[4]。然而，传统声发射采集信号是间断性、非连续的信号，采集不到完整的周期信号；而声发射波形流技术能够将波形数据连续的记入计算机的物理内存，以高采样率完成固定长度的声发射周期性信号采集，为后期分析提供完整可靠的数据。另外，对采集到的声发射波形流信号进行双谱分析，通过双谱分析三维图及等高线图，可以表现出滑动轴承不同故障类型的特征，据此判断轴承故障的产生及类型。

1 非接触式声发射检测与波形流技术

滑动轴承在运转过程中产生的信号是平稳的连续性信号；但出现故障时，缺陷位置会产生突发型的撞击信号，并且呈周期性出现。声发射检测技术的基本原理就是用灵敏仪器接收和处理采集到的声发射信号，通过对声发射源特征参数的分析和研究，推断出材料或结构内部活动缺陷的位置、变化程度和发展趋势[5]。结合声发射检测技术的原理，滑动轴承故障非接触声发射检测的原理如图1所示[6]。

波形流技术能够获取完整的声发射信号，在周期性声发射数据的采集上得到广泛的应用，轴承的声信号就具有周期性，所以更能体现波形流功能的优势。运用声发射波形流技术可以实时、长时间地采集连续型声发射信号，后续分析时既可以查看多周期特点，也可以对局部波形进行放大分析。运用波形流技术采集到的声发射信号如图2所示，该信号采样率为1 MHz，采样时长为1 s。局部峰值放大信号是原信号被2条直线分割后放大的波形，被放大的部分是一个典型的声发射突发型信号。

图2 声发射波形流信号示意图

2 滑动轴承模拟故障声发射测试

2.1 测试系统

测试系统由滑动轴承模拟故障测试试验台和声发射信号采集系统组成。如图3所示，采用RK-4 Rotor Kit型转子试验台，调速范围为200～10 000 r/min，能够模拟实际的转子工况。

图3 滑动轴承模拟故障试验台

采用PCI-2型声发射检测系统来获取波形流。该系统选用WD宽带传感器，2/4/6型前置放大器，传感器安装在中点位置的轴支承架上。waveform streaming(波形流)设置位于 Acquisition Setup(采集设置)菜单项下的 Hardware(硬件)菜单项中,采用人工触发的方式。在采集过程中使用流功能时，Enable streaming必须选中。进行多次模拟采集试验，研究波形流的各个采集参数对试验结果的影响。设置门槛值类型为固定型,门槛值为30 dB,波形设置中采样率为1 MHz，预触发时间设置为1.024 ms，可记录长度为500 s。

2.2 模拟故障试验

采集不同转速下同一故障和同一转速下不同故障的声发射波形流信号进行分析，分别研究转速对滑动轴承故障特征的影响和不同故障的声发射波形流信号特征。具体试验方案如下：

1)设定9组不同转速，分别为240，720，1 200，2 160，2 640，3 120，3 600，4 080和4 560 r/min。采集这些转速下不同故障的声发射波形流信号，研究转速对滑动轴承故障特征的影响。

2)模拟不同的故障，分析同一转速下不同故障所表现的不同特征。在转子的平衡盘上加平衡重模拟不平衡状态；手持摩擦棒，在转子旋转的过程中保持摩擦棒顶端与转子表面始终处于接触状态，模拟转子的碰摩状态；将滑动轴承的轴承座倾斜一个角度，使转子和轴承形成不对中状态。分别采集在上述9种转速下不平衡故障、摩擦故障和不对中故障的声发射波形流数据。

3 模拟故障声发射波形流信号的分析

3.1 时域分析

3.1.1 不同转速

2个传感器采集到的信号基本一致，因此只对通道1传感器采集到的数据进行分析。提取不同转速下各种故障状态的声发射波形流峰值信号，结果见表1。由表可知：随着转速的增加，正常和各个故障状态的峰值都呈增长趋势。转子转动达到一定的转速会产生共振，共振时波形图中产生明显的波峰，波形的幅值明显增大，峰值电压值明显高于其前后各相邻转速下的峰值电压值。

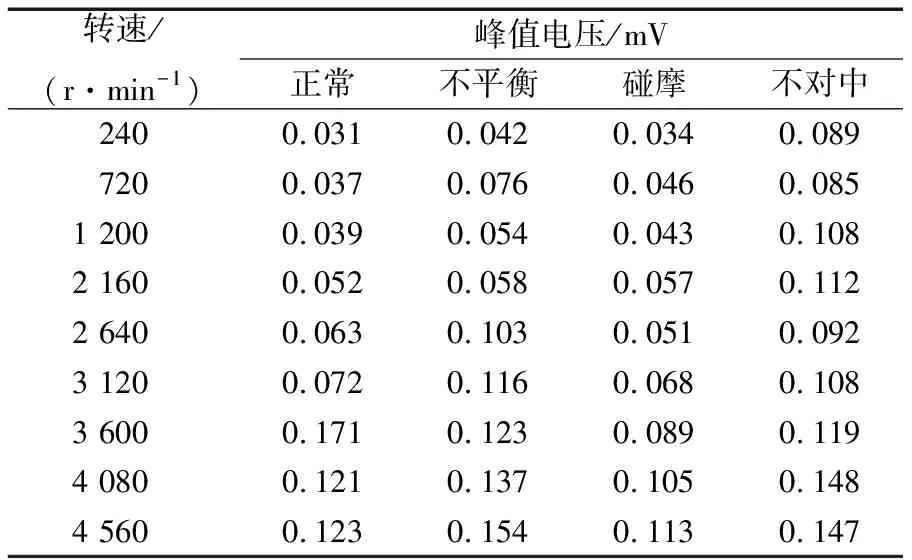
表1 不同故障声发射信号时域图的峰值电压

3.1.2 同一转速

当转子转速为1 200 r/min时，各种状态都没有出现共振现象，该转速下10个周期的声发射波形流信号时域图如图4所示。在1 200 r/min的转速下，0.5 s的采样时间内理论上应该出现10个周期，实际测试结果与理论值完全吻合。体现了声发射信号的高灵敏度，证明波形流数据能够采集到完整的周期性声信号。

图4 1 200 r/min下的声发射信号时域图

正常状态下滑动轴承的峰值电压为0.039 mV，采集到的声发射波形流信号是连续、平稳的信号。滑动轴承处于故障状态时，可以明显看出时域图中有突发型的峰值电压，图中出现1次波峰代表实际测试中故障撞击了1次。从图中可以看出：滑动轴承处于不平衡状态时，峰值电压约0.054 mV；处于摩擦状态下的峰值电压约0.043 mV；不对中状态下采集到的声发射波形流信号中峰值电压增加最明显，约为0.108 mV。说明在相同转速下，故障状态的峰值电压值高于正常状态的峰值电压，根据时域图能够初步判断是否发生故障，但是不能体现每种故障的特征，还需对数据进行进一步分析。

3.2 双谱分析

滑动轴承的声发射信号是非高斯、非线性的。高阶谱分析对高斯噪声具有不敏感性，在抑制噪声方面具有显著的效果，为强噪声背景下的微弱、复杂信号检测提供了一个新的途径和方法。高阶谱中的双谱分析方法最简单，不仅弥补了功率谱中不包含相位信息的缺陷，还能有效地抑制噪声，揭示信号频率之间的非线性耦合现象，突出故障特征频率[7]，从而确定故障类型。

3.2.1 基于MATLAB的双谱分析实现

进行双谱分析时声发射波形流信号的点数不能太多。以1 200 r/min为例，该转速的周期为50 ms，原采样频率为1 MHz，1个完整周期的波形流数据中共包含50 000个数据点，数据点太多，程序计算困难。运用MATLAB以50 kHz的采样频率对50 ms时间内的数据进行重新采样，碰摩故障的原始数据和重新采样后数据的功率谱如图5所示。对比分析可知：2种信号的频率、幅值、分布均无变化，只是功率谱密度有所下降，所以重新采样后信号能够满足继续分析的要求。双谱程序能够对此数据进行分析，不会丢失数据的频率成分。

图5 碰摩故障信号的功率谱

3.2.2 典型故障波形流信号的双谱分析

对1 200 r/min转速下各信号重新采样，取1个完整周期的数据进行双谱分析，由于双谱分析具有对称性和周期性，仅分析第1象限中的下三角区域。

滑动轴承处于正常状态时(图6)，峰值频率出现在[11 kHz,11 kHz]，[18 kHz,13 kHz]，[13 kHz,18 kHz]和[18 kHz,18 kHz]等处，幅值为0.18～0.25 μV，峰值频率周围出现了很多幅值相对较低的频率，频率分布较分散。

图6 正常状态双谱分析三维及其等高线图

当滑动轴承出现不平衡故障时(图7)，峰值频率出现在[18 kHz,13 kHz]，[13 kHz,18 kHz]和[18 kHz,18 kHz]处，幅值为2.0～2.5 μV，除出现3个峰值频率外，其他的频率很少，频率分布较为单一，幅值相对较低的其他频率出现很少。

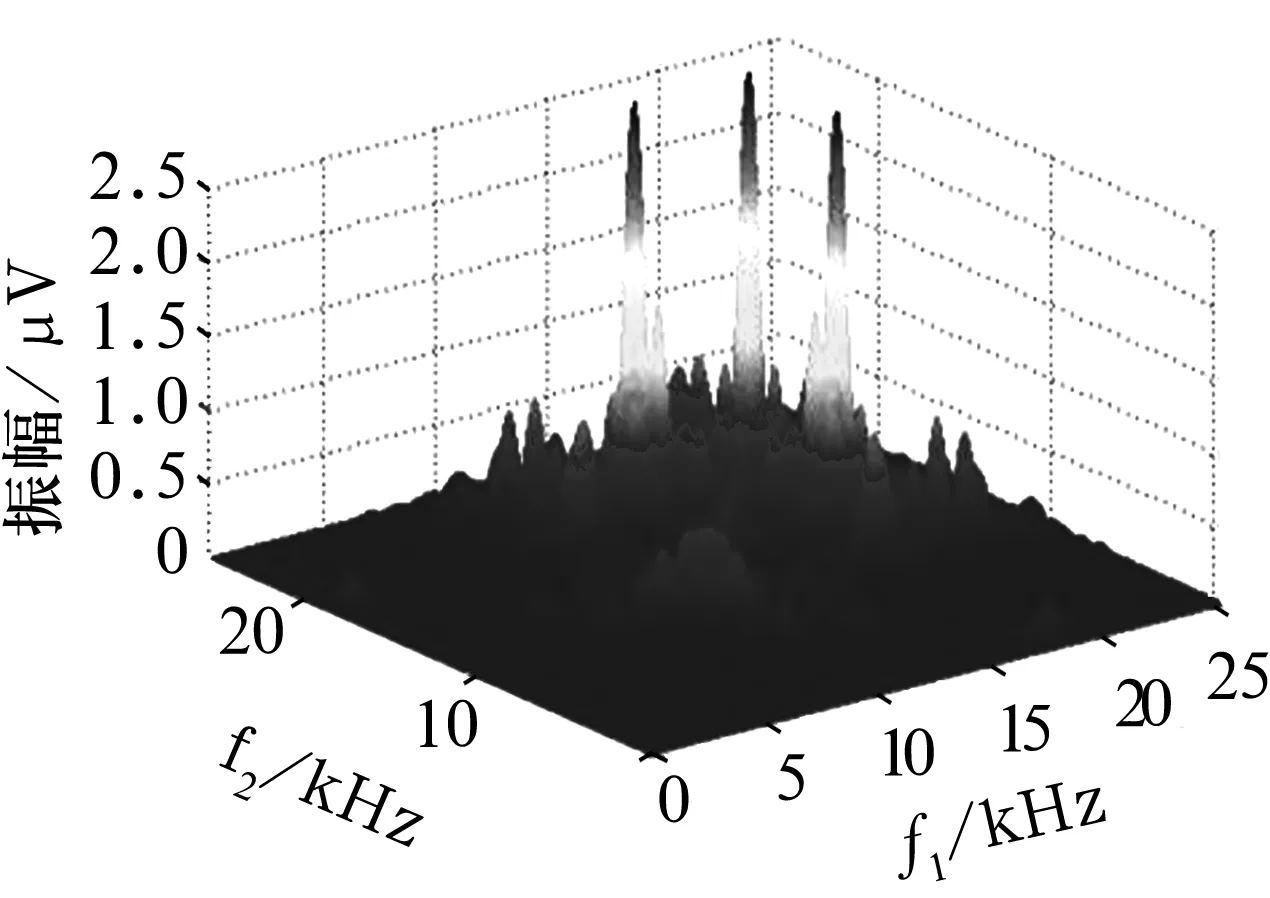
图7 不平衡故障双谱分析三维及其等高线图

当滑动轴承处于碰摩故障状态时(图8)，峰值频率也出现在[18 kHz,13 kHz]，[13 kHz,18 kHz]和[18 kHz,18 kHz]处，幅值为2.0～2.5 μV，但是从等高线图中发现，3个峰值频率的外围没有其他频率分布，只是在3个峰值频率的中间有其他频率出现。

图8 碰摩故障双谱分析三维及其等高线图

当出现不对中的故障时(图9)，峰值频率集中出现在[18 kHz,16 kHz]，[18 kHz,18 kHz]， [17 kHz,16 kHz]和[17 kHz,17 kHz]等处，幅值为2.5～3.0 μV，除了几个峰值频率外没有其他频率分布。

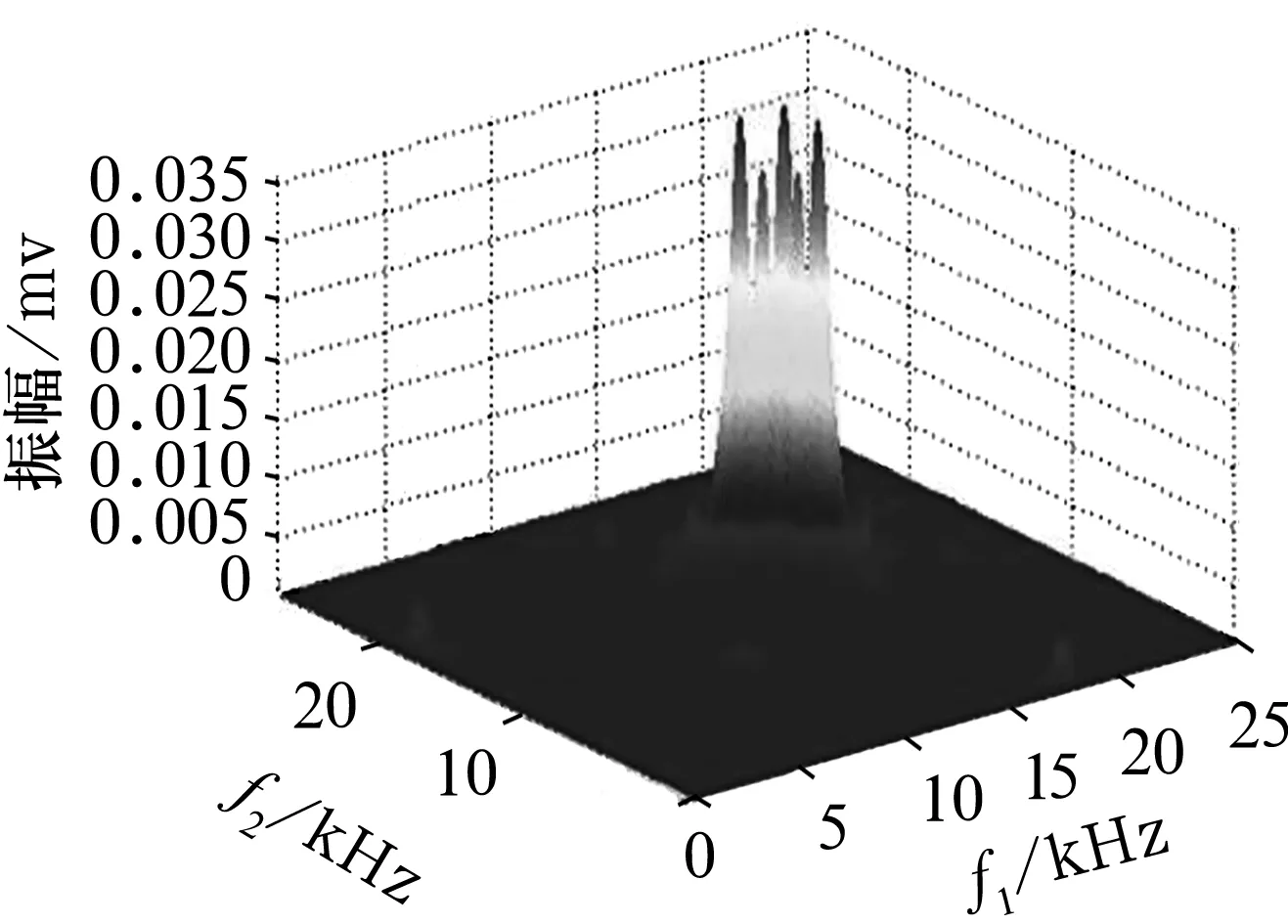
图9 不对中故障双谱分析三维及其等高线图

双谱分析体现了频率的相位信息，滑动轴承出现不同故障时，经过双谱分析所测得的峰值频率出现在固定的位置，当转速发生变化时，故障峰值频率出现位置不变，但幅值会随之改变。根据每种故障状态的峰值频率分布及幅值大小，可以判断出滑动轴承的故障类型，实现对滑动轴承的故障诊断。

4 结论

1)声发射波形流信号采集技术可获得连续不间断的多周期声发射信号，此信号包含完整的轴承声信息，分析时既可以查看多周期的波形流数据，同时也可以对局部波形进行放大分析研究，使声发射技术对轴承故障的诊断更加准确。

2)随着转速的增加，正常状态和各个故障状态下的峰值都呈增长趋势。当转子转动达到一定的转速会产生共振，共振时波形图中产生明显的波峰，波形的幅值也明显增大。

3)轴承处于正常状态时产生的声发射波形流信号是连续的、平稳的信号。当滑动轴承出现故障时，同一转速下会出现峰值电压明显增高的情况，可以根据峰值电压的数值判断是否发生故障。

4)采用双谱分析方法对滑动轴承不同状态声发射波形流信号进行分析，不同状态下的三维图及其等高线图均表现出明显不同的特征，据此可有效判断故障类型。