基于改进匈牙利算法的多技能人员调度方法*

李廷鹏，钱彦岭，李　岳

(国防科技大学 装备综合保障技术重点实验室， 湖南 长沙　410073)



基于改进匈牙利算法的多技能人员调度方法*

李廷鹏，钱彦岭，李岳

(国防科技大学 装备综合保障技术重点实验室， 湖南 长沙410073)

摘要：人员的优化配置对于提高装备制造效率具有重要意义。针对经典匈牙利算法不能解决具有并联环节的人员指派问题的不足，提出利用虚拟工作代替并联环节，将问题转化为典型的指派问题；通过判断虚拟工作的可实现性，迭代搜索得到最优解。以某多技能人员任务指派系统为例，详细介绍了该优化方法的步骤。优化结果很好地验证了改进算法的有效性。

关键词：匈牙利算法；装备制造；资源调度；虚拟工作；多技能

随着人力成本的增加，使用多技能工人已逐渐成为提高人员利用率的重要途径。针对具体任务，如何优化人员配置，更加合理地发挥各个人员的特长是人员调度问题的关键所在。指派问题是人员调度问题中的经典问题——m个人完成n项工作，且每个人完成每项工作的效率不一样，确定任务指派方案使得完成任务总的效率最高。

解决指派问题的方法主要有两类：一类是确定性解析算法——匈牙利算法；另一类是启发式智能算法，比如遗传算法[1]、模拟退火算法[2]、蚁群算法[3-4]等。启发式算法对于大规模的指派问题具有速度较快的优势但不能保证能得到最优解，而且算法相对复杂，在工程实际中应用并不多。匈牙利算法具有步骤简单、能得到最优解且无须验证的特点，被广泛用于解决中小规模的指派问题[5-6]。

文献[5-6]在剖析匈牙利算法的基础上，对匈牙利算法进行了改进，提出“加边补零法”用于解决不完全指派问题。文献[7]给出了匈牙利算法MATLAB实现的通用程序，并用于解决婚配等典型的指派问题。文献[8]提出了差额法解决非标准型指派问题，与传统算法相比，更加简洁、直观。文献[9]应用匈牙利法解决了不正常航班的应急调度问题，取得了较好的效果。文献[10]利用改进的匈牙利算法研究了恶劣环境下多个维修活动的调度问题。文献[11]应用进化匈牙利算法解决无人机目标分配问题。文献[12]提出将匈牙利算法与拓扑约束相结合进行高密度条件下的细胞追踪研究。文献[13]为了提高云计算任务的分配效率，在标准匈牙利算法的基础上提出一种快速降阶优化算法，该算法通过不断排除代价矩阵中已经确定的元素，快速降低矩阵的阶次，提高了匈牙利算法的计算效率。文献[14]将火力分配问题转换为指派问题，利用匈牙利法对武器-目标动态火力配置进行了研究。

虽然匈牙利算法已经在实际中得到了较大的应用，并取得了较好的效果。但是传统的匈牙利算法只能针对“总代价为各个任务代价之和”一类问题进行求解，而在实际工程中，许多情况并不满足这个条件。因此，需要对算法进行改进，以便其能更好地解决实际问题。

1经典匈牙利算法及应用上的不足

1.1经典匈牙利算法

经典匈牙利算法是Kuhn利用匈牙利数学家Koning关于矩阵中独立零元素定理提出的用于解决指派问题的优化方法[10]。该方法的理论基础是：在效益矩阵(也称代价矩阵)的任意行或列加上或者减去一个常数不会改变最优分配方案[15]。其基本思想是通过每行或每列加减同一个常数来修改效益矩阵，直到效益矩阵不同行不同列至少有一个零元素，且零元素就对应了一个总效益最小的最优分配方案。

经典匈牙利算法的基本步骤如下：

步骤1：建立资源分配问题的效益矩阵M0(m×n)。

步骤2：从效益矩阵M0每行减去该行最小的元素，使得每行都有一个零元素，得到M1。

步骤3：从M1每列减去该列最小的元素，使得每列都有一个零元素，得到M2。

步骤4：用最少的直线覆盖M2中的零元素得到M3，如果最少直线的数量等于m，转入步骤6，否则转入步骤5。

步骤5：矩阵M3中所有未被直线覆盖的元素减去未被覆盖元素中最小的元素，同时在直线相交点加上该最小元素得到M4，令M2=M4，转步骤4。

步骤6：从零元素最少的行或列开始指派，直到所有任务都指派完毕，得到最优指派方案P。

上述步骤中，假定的是m=n，即效益矩阵M0是一个方阵。但在实际问题中，任务数与人数不一定完全相等。针对任务数与人数不相等的情况，一般的处理方式是增加虚拟人或虚拟任务，即对效益矩阵进行加零补边处理，然后再按照上述步骤进行任务指派，具体方法参考文献[5]。

1.2应用中的不足

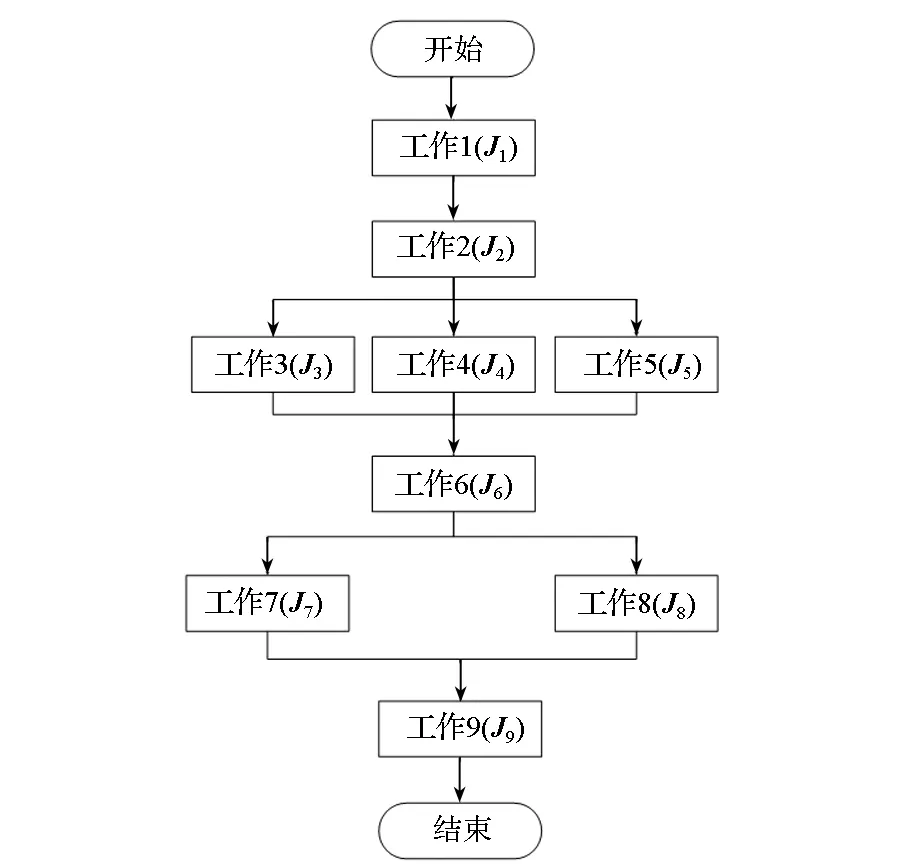
经典匈牙利算法自提出以来就受到了广泛的关注，也解决了不少的工程实际问题。但传统的匈牙利算法只能针对总效益为各个任务效益之和的情况进行任务指派。假设效益是用各个任务的时间表示，那么传统的匈牙利算法只能对串联工作进行任务指派，即总时间为各个任务时间之和。但在工程实际中，特别是装备制造系统中，串并联同时存在是很常见的情况，比如：有4项工作需要完成，工作的先后顺序如图1所示。4个工人完成各项工作的时间已知，且每个工人只能完成一项工作，问题是如何安排4个工人的工作任务使总时间最少。

分析该问题可以发现，传统的匈牙利算法已经不能直接拿来解决此问题，因为工作2和工作3需要耗费较长的时间才会对总时间产生影响，即各个工作加工时间对总时间的贡献并不处于平等的地位。为了解决此类问题(串并联并存)，提出了改进的匈牙利算法。

2改进匈牙利算法

2.1算法改进的基本思路

由前面的分析可知，传统的匈牙利算法之所以不能解决与1.2类似的问题，主要是因为并联部分的工作总时间并不是各项工作的时间之和，而是由其中的最大值决定。所提出的解决思路是将串并联系统分成两个部分——串联部分和并联部分(可能有多个)，分别用虚拟工作代替各并联部分的所有工作，使得整个系统变成纯串联系统。在此基础上利用传统的匈牙利算法进行任务指派，然后再判断指派方案中的虚拟工作能否按照预定的最小时间转换为并联工作实现，如果可以则得到了最优分配方案并结束，否则增加虚拟工作对应的时间，甚至重新分配。

2.2改进匈牙利算法详细步骤

基于以上思路，针对串并联并存的任务指派问题，改进匈牙利算法的流程图如图2所示。

图2　改进匈牙利算法流程图Fig.2　Flow-chart of the improved Hungary algorithm

算法的详细步骤如下：

步骤1：将系统分为串联部分和并联部分(如果有多个并联环节则每个并联环节独立为一部分)，即：

S=C+Bi,i=1,2,…,n

(1)

式中，S代表整个系统，C代表所有串联的工作，Bi代表并联环节i，n为并联环节的个数。

步骤2：利用虚拟工作Jvi代替并联部分i的工作，同时初始化虚拟工作的各个人员完成时间。

(2)

式中，Tvij表示人员j完成虚拟工作i需要的时间。

虚拟工作Jvi的初始值设定为各个人员完成虚拟工作i的理论最小时间Tij_min。

理论最小时间Tij_min指的是在人员j参与并联环节i的某项工作的前提下，并联工作可能完成的最小时间，即：

Tij_min=min(Tij_1,Tij_2,…,Tij_k)

(3)

式中，Tij_p(p=1,2,…,k)表示人员j完成并联环节i中的第p项工作需要的时间。

那么，初始虚拟工作为：

(4)

步骤3：利用原系统中的串联工作和虚拟工作Jv构建新的纯串联系统。

步骤4：利用传统的匈牙利算法对S_new进行任务指派，得到分配方案P。

步骤5：判断分配方案P中所有虚拟工作Jv是否可实现，如果可以转步骤8，否则转步骤6。

虚拟工作Jvi可实现是指可以由方案P中的被指派到虚拟工作Jvi的人员以及空闲人员在虚拟工作规定的时间内完成并联环节i的工作。

由于每人只能完成一项工作，因此，虚拟工作的可实现方案不能相互冲突，否则认为Jv不可实现。

步骤6：如果方案P中虚拟工作Jvi可实现最小时间小于虚拟工作i对应的时间Tviq，即：

Tviq>min(TBi)

(5)

其中TBi表示并联环节i在方案P中被指派到虚拟工作Jvi的人员参与下的所有可实现的完成时间。

那么，Tviq增加一个单位。即：

Tviq=Tviq+1

(6)

步骤7：如果方案P中虚拟工作Jvi可实现最小时间大于虚拟工作对应的时间Tviq，

Tviq

(7)

则Tviq减少一个单位，然后转步骤3。即：

Tviq=Tviq-1

(8)

将虚拟工作对应时间减少称之为过优回退原则，设置过优回退原则的目的是为了避免遗漏最优解。

步骤8：用可实现的并联工作方案代替分配方案P中的虚拟工作，得到最终的最优分配方案P*，优化结束。

3实例验证

为了更详细地介绍所提出的改进匈牙利算法的步骤，验证算法的有效性，并给出了一个多技能人员任务指派系统的实例。

3.1问题描述

某多技能人员任务指派系统任务流程如图3所示，共有9项工作，其中有两个并联环节，分别记P1(J3，J4，J5)和P2(J7，J8)。该系统总的任务时间为Tall：

Tall=T1+T2+max(T3,T4,T5)+T6+max(T7,T8)+T9

(9)

其中Ti(i=1,2,…,9)代表各个工作需要的时间。

图3　某装备系统制造流程图Fig.3　Manufacturing flow-chart of the equipment

现有9名工人，并已知每名工人完成各个工作需要的时间，见表1。

表1　工人完成各项工作需要的时间

表中，Ri(i=1,2，…，9)分别代表9名工人，Ji(i=1,2，…，9)分别代表9项工作，时间单位为min。要求每名工人有且完成一项工作，寻找最优的任务分配方案。

3.2多技能人员任务调配

1) 确定并联环节，同时计算并联环节虚拟工作的各个人员最小完成时间。

分析图3可知，该系统共有两个并联环节，分别是P1(J3，J4，J5)和P2(J7，J8)。利用虚拟工作1(Jv1)和虚拟工作2(Jv2)代替并联环节，得到新的系统，如图4所示。

图4　替换后系统的流程图Fig.4　Flow-chart of the replaced system

其中，

(10)

其中Tvi_j(i=1,2;j=1,2,…,9)表示工人j完成虚拟工作i需要的时间。

为了提升算法速度，首先计算出虚拟工作各个工人完成的最小虚拟时间，得到最小时间虚拟工作Jv1_min和Jv2_min。

(11)

2) 利用最小时间虚拟工作(Jv1_min，Jv2_min)以及串联部分的工作(J1,J2,J6,J9)构建效益矩阵M0:

(12)

3) 按照传统的匈牙利算法得到M0的最优分配方案。

由于M0并不是一个方阵，按照文献[2]“加零补边法”的步骤，可以得到M0对应的最优分配方案。

(13)

最优方案如表2所示,方案对应的时间为125 min。

表2　M0对应的最优分配方案

4) 判断M0对应的最优分配方案中，并联环节能否实现。

从表2中可以看到，M0对应的最优方案要求R8与R1，R2，R3中的任意两个在32 min内完成并联环节P1的工作(J3, J4, J5)。同时要求R7与R1，R2，R3剩下的那个在12 min内完成并联环节P2的工作(J7, J8)。

简单分析就可以发现，R8与R1，R2，R3中任意两个完成并联环节P1最小花费时间为43 min。且R7与R1，R2，R3中任意一个完成并联环节P2最小花费时间为25 min。因此M0对应的最优方案中的虚拟工作不能转化为可实现的并联环节，也就是说此时的最优方案不可实现。

根据改进的匈牙利算法的步骤，需要将两个虚拟工作对应的时间(M0的最优方案中虚拟工作Jv1和Jv2对应的时间，即Tv1_8,Tv2_7)提高一个单位，即Tv1_8：32→33，Tv2_7：12→13，得到新的虚拟工作。

(14)

利用Jv1，Jv2以及J1，J2，J6，J9构建效益矩阵M1，返回3)继续搜索直到得到可行最优解。

3.3优化结果及分析

利用MATLAB 2008a在主频为3.4 GHz的Window XP平台上编程实现，经过87次迭代，最终得到了最优调配方案见表3，总的时间为147 min，且此时迭代的虚拟工作为：

(15)

利用可实现并联环节替代表3中的虚拟工作，得到完整最优分配方案见表4。

表4　完整最优分配方案

为了验证本算法得到的最优解是否为全局最优，本文在相同的平台上通过MATLAB编程遍历了所有可能的方案(共362 880个)，找到最优的分配方案见表5。

表5　遍历结果中的最优方案

对比表4和表5，可以发现，本文改进的算法的确得到了全局最优解。

4结论

针对传统的匈牙利算法不能用于解决具有并联环节的资源调配问题，提出利用等价虚拟工序代替并联环节的方式，将问题转化为常规指派问题，通过判断等价虚拟工序能否在并联环节中实现，逐步提高虚拟工作对应点的时间，以反复迭代的方式搜索可实现方案，同时为了避免漏掉最优解，提出了过优回退原则。最后的实例验证了该算法的有效性，拓展了匈牙利算法的应用范围。

参考文献(References)

[1]陶世群， 蒲保兴． 基于遗传算法的多级目标非平衡指派问题求解[J]．系统工程理论与实践， 2004， 24(8)： 80-86.TAO Shiqun, PU Baoxing. Solving multi-object and unbalanced assignment problem based on genetic algorithm[J].System Engineering-Theory & Practice, 2004, 24(8): 80-86.(in Chinese)

[2]李冰， 徐杰， 杜文． 用模拟退火算法求解有顺序约束指派问题[J]．系统工程理论方法应用，2002，11(4)：330-335.

LI Bing, XU Jie, DU Wen. A simulated annealing algorithm for an assignment problem with precedence relation among the elements[J]. Systems Engineering—Theory Methodology Applications, 2002, 11(4): 330-335. (in Chinese)

[3]殷人昆， 吴阳， 张晶炜． 蚁群算法解决指派问题的研究和应用[J]．计算机工程与科学， 2008， 30(4)： 43-45.

YIN Renkun,WU Yang, ZHANG Jingwei. Research and application of the ant colony algorithm in the assignment problem[J]. Computer Engineering & Science, 2008, 30(4): 43-45. (in Chinese)

[4]梁耀， 覃征， 杨利英， 等． 指派问题的变异蚁群算法求解[J]．微电子学与计算机， 2005， 22(6)： 80-83.

LIANG Yao, QIN Zheng,YANG Liying, et al. Mutated ant colony algorithm for assignment problem[J]. Microelectronics & Computer, 2005, 22(6): 80-83. (in Chinese)

[5]陈元明．匈牙利算法的注记[J]．丽水学院学报， 2011， 33(5)： 78-81.

CHEN Yuanming. A note on Hungary algorithm [J]. Journal of Lishui University, 2011, 33(5): 78-81. (in Chinese)

[6]杜金玲， 周杰． 关于几种不平衡指派问题的修正匈牙利解法[J]．价值工程， 2010， 2010(13)： 120-122.

DU Jinling, ZHOU Jie. Fixed Hungary algorithm to unbalanced assignment problems [J]. Value Engineering, 2010, 2010(3): 120-122. (in Chinese)

[7]常庭懋， 韩中庚．用“匈牙利算法”求解一类最优化问题[J]．信息工程大学学报， 2004， 5(1)： 60-62.CHANG Tingmao, HAN Zhonggeng. Solution to a class optimization problem by utilizing the “hungary calculate way” [J]. Journal of Information Engineering University, 2004, 5(1): 60-62. (in Chinese)

[8]马晓娜．“人少任务多”型指派问题的一种新算法术[J]．重庆工商大学学报(自然科学版)， 2014， 31(12)： 68-71.

MA Xiaona. A new algorithm for assignment problems with“tasks more than the number of persons” [J]. Journal of Chongqing Technology and Business(Natural Sciences Edition), 2014， 31(12)： 68-71. (in Chinese)

[9]赵万林．不正常航班应急调度的模型与算法[D]．天津:中国民航大学， 2014.

ZHAO Wanlin. Model and algorithm for the irregular flight emergency scheduling[D]. Tianjin:Civil Aviation University of China, 2014. (in Chinese)

[10]仇勇．恶化环境下带多个维修活动的调度算法研究[D]．杭州:浙江工商大学， 2013.

QIU Yong. Study on scheduling algorithm with deteriorating jobs and multiple maintenance activity [D]. Hangzhou:Zhejiang Gongshang University, 2013. (in Chinese)

[11]谷稳．基于进化匈牙利算法的目标分配问题研究及应用[D]．西安:西安电子科技大学， 2013.

GU Wen. A study and application of target allocation based on evolution Hungary algorithm [D]. Xi′an:XiDian University, 2013. (in Chinese)

[12]董莎莎．基于拓扑约束和匈牙利算法的高密度细胞追踪方法[D]．哈尔滨:哈尔滨工程大学， 2011.

DONG Shasha. The method of high density cells′tracking based on Topological constraint combined with Hungarian algorithm [D]. Harbin: Harbin Engineering University, 2011. (in Chinese)

[13]何富江, 任金霞． 快速降阶匈牙利算法的云计算任务分配模型[J]．江西理工大学学报， 2014， 35(3)： 63-67.

HE Fujiang,REN Jinxia. Task assignment model in cloud computing based on Hungary algorithm of faster reduced order[J]. Journal of Jiangxi University of Science and Technology, 2014, 35(3): 63-67. (in Chinese)

[14]李建立．武器-目标动态火力分配及战效评估的研究[D]．南昌:南昌航空大学， 2014.

LI Jianli.Research on weapon-target dynamic assignment and effectiveness evaluation[D]. Nanchang :Nanchang Hangkong University, 2014. (in Chinese)

[15]宋雨晴．指派问题的改进算法[J]．科技视界， 2012(14)： 106-108.

SONG Yuqing. The improved algorithm for assignment problem [J].Science & Technology Vision, 2012(14)： 106-108. (in Chinese)

doi:10.11887/j.cn.201602024

*收稿日期：2015-05-06

基金项目：部委级重点预研基金资助项目(9140C710301150C71001)

作者简介：李廷鹏(1987—)，男，重庆人，博士研究生，E-mail:tovey1987@126.com; 李岳(通信作者)，男，教授，博士，博士生导师，E-mail:liyue@nudt.edu.cn

中图分类号：TN95

文献标志码：A

文章编号：1001-2486(2016)02-144-06

Multi-skilled labor allocating method based on improved Hungary algorithm

LI Tingpeng, QIAN Yanling, LI Yue

(Science and Technology on Integrated Logistics Support Laboratory, National University of Defense Technology, Changsha 410073, China)

Abstract：The optimal allocation of labor is of great significance to improve the efficiency of equipment manufacturing. For the shortcoming of traditional Hungary algorithm could not solve the resource scheduling problem with parallel links, an improved Hungary algorithm was proposed. The improved algorithm converted the problem into a typical assignment problem by replacing parallel link jobs with virtual jobs, and optimized it with classical Hungary algorithm and determined the realizability of the virtual jobs based on the results. Finally, the optimal scheme was obtained through iterative searching. In addition, an example of multi-skilled labor allocation system is introduced to verify the effectiveness of the proposed algorithm.

Key words：Hungary algorithm; equipment manufacturing; resource scheduling; virtual jobs; multi-skill

http://journal.nudt.edu.cn