高超声速飞行器常规螺线管磁控热防护系统可行性分析*

李　开，刘伟强

(国防科技大学 航天科学与工程学院， 湖南 长沙　410073)



高超声速飞行器常规螺线管磁控热防护系统可行性分析*

李开，刘伟强

(国防科技大学 航天科学与工程学院， 湖南 长沙410073)

摘要：针对高超声速飞行器鼻锥热防护，构造常规圆柱螺线管磁控热防护系统的物理模型。采用低磁雷诺数磁流体数学模型，对外加磁场作用下的高超声速鼻锥流场进行数值模拟；分析常规螺线管磁控热防护系统的有效磁感应强度范围；给出满足导线电流密度工作极限的螺线管几何参数的要求。研究表明，由于磁控“饱和现象”及导线电流密度的限制，系统可行工作范围为驻点磁感应强度B0∈[0.05 T,0.20 T]；B0=0.20 T时，驻点热流密度和总热流分别降低了31.3%和56.6%，热防护效果良好；但磁控系统导线质量仍然较重，应采用可缩短与驻点间距离的异形螺旋管或超导磁铁等替代方法来满足工程防热需求。

关键词：磁流体控制；高超声速飞行器；热防护；螺线管磁铁

未来临近空间高超声速飞行器的飞行条件将会越来越恶劣，热防护问题也将越来越突出。由于传统瓦热防护方法存在可重复性差、容错率低等弊端，近年来学者们提出了许多新型热防护的概念并进行了大量可行性研究，如充气式防热罩[1]、凹腔逆喷[2]、层板发汗[3]、疏导式防热[4]等。

磁控热防护的概念最早诞生于20世纪50年代末[5]，原理如图1所示(图中J为感应电流密度，B为磁感应强度)。磁铁位于返回舱内部。当磁场作用于头部微电离等离子区域时，激波层内的环形感应电流和磁场相互作用会产生与流动方向相反的洛伦兹力，减速等离子流并将激波推出，从而降低表面温度梯度，实现热防护。磁控热防护系统的能量来源为电能，可以使用机载电源；并且其位于防热材料以内，不会改变飞行器的表面结构，可靠性高，可根据需要开闭，可和其他被动热防护方法配套使用，很符合未来高超声速飞行器可重复使用的要求。

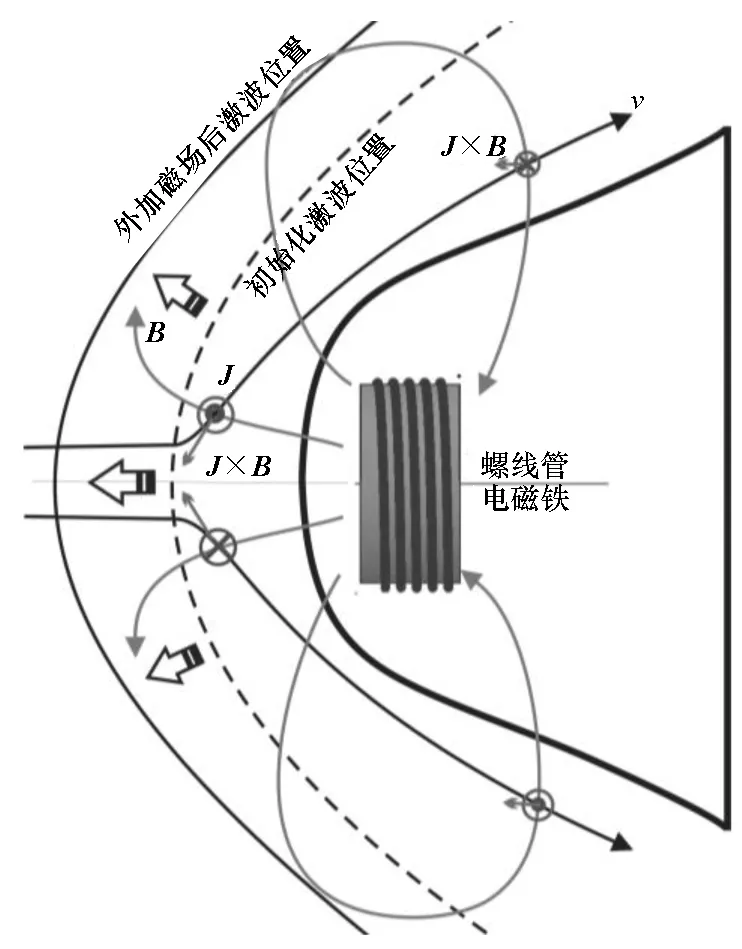
图1　磁控热防护系统原理图Fig.1　Schematic of magnetohydrodynamic heat shield system

20世纪末以来，磁控热防护技术出现了一个新的研究热潮[6]，这得益于以下原因：①能量旁路超燃冲压发动机的提出[7]；②高焓风洞试验条件的进步；③稀土磁铁、超导磁铁技术的发展；④高温磁流体力学的发展[8]等。其中，俄高温研究所Bityurin等首次研究了直径不同的两种外加电磁铁磁场热防护效果的差异[9]以及烧蚀条件下的磁控热防护效果[10]；美空军研究实验室的Bisek等首次提出了头部浸渍碱金属烧蚀材料提高流场电导率进行翼前缘磁控热防护的概念[11]；日本的Fujino等研究了霍尔效应、壁面电导率对磁控热防护效果的影响，结果表明在绝缘壁面可以忽略霍尔效应对磁控热防护的副作用[12]；欧航局近些年资助德国和意大利航天中心开展了磁控热防护试验研究[13]，试验表明，添加磁场后，球头圆柱表面温度和热流分别降低16%和46%[14]。磁控热防护系统的有效性得到了大量的证明。

目前，磁控热防护的数值研究主要基于简化的磁偶极子模型[5,10]，针对较为实际的常规圆柱螺线管磁控系统的可行性研究还未见诸文献。本文从有效工作的磁感应强度范围、导线电流密度、导线长度(质量)等角度分析了磁控热防护系统的工程可用性。

1螺线管磁控物理模型

常规螺线管磁控系统的物理模型如图2所示。图中弧形实线代表飞行器前体外表面，矩形为螺线管，半径为rM，半长为bM，螺线管中心坐标为(zC,0)，磁铁两端面的轴向坐标分别为(z1,0)和(z2,0)。P为流场中一点，Q为螺线管载流线圈上一点。

图2　螺线管磁控系统模型Fig.2　Physical model of solenoid-based magnetohydrodynamic system

流场区域磁感应强度B依据Bivot-Savard定律求解，并假设螺线管由很多个圆环线圈叠加而成，只产生轴对称的磁场。可得P(z,r)点磁感应强度分量如式(1)、式(2)所示。其中，μ0为真空磁导率，n为单位长度线圈匝数，I为励磁电流。fz和f包含三类椭圆积分，其迭代算法及k1和k2的含义见参考文献[15]。

(1)

(2)

2数学模型

磁流体流场数值模拟主要依据Maxwell方程组、广义欧姆定律以及包含电磁源项的磁流体方程。高超声速飞行器等离子体鞘内电导率较低，并且研究对象为轴对称磁流场问题，可做以下假设：①等离子体电中性假设；②忽略位移电流；③非相对论流动；④忽略霍尔效应；⑤低磁雷诺数假设；⑥忽略感应电场。控制方程如式(3)～(5)所示。其中，E，F为无黏通量项；Ev,Fv为黏性通量项；G和Gv分别为无黏和黏性源项；u,v分别为z,r向速度；ρ和et分别为密度和总能；J和Ee分别代表感应电流和电场场强。

(3)

(4)

(5)

对于轴对称磁流体问题，忽略感应电场后，能量方程电磁源项为零，并且激波层内的感应电流密度只有周向分量，由广义欧姆定律得：

jθ=σ(uzBr-urBz)

(6)

其中，电导率σ计算采用Raizer模型[16]。流场电导率仅和静温有关，并且按照类似阿雷尼乌斯公式的规律变化。

对流项差分采用了AUSMPW格式，方程求解采用了LU-SGS隐式格式，对电磁源项采用了隐式处理以提高收敛性。图3对比了三个网格雷诺数(2，5，10)下的热流计算结果与Miller的试验结果[17](L为参考长度，Qw为表面热流密度)，其中第四套网格与第二套网格雷诺数相同而法向进一步加密。可以看出，四套网格下的热流计算结果与试验结果吻合良好，从而验证了气动热数值方法的准确性。

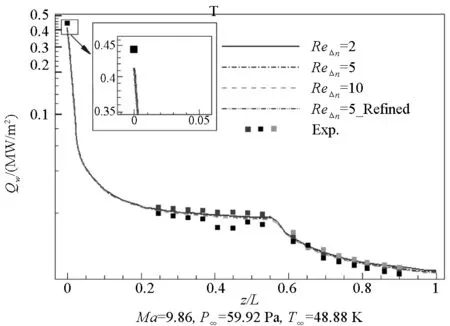
图3　热流计算结果与Miller试验结果的对比Fig.3　Comparison of heat flux between computational results and Miller′s results

3计算条件

几何模型选择日本的OREX(Orbital Re-entry EXperiment)返回舱，并选择气动热最为严重的飞行工况：U∞=6223.4 m/s，H=63.6 km。采用等温壁模型，壁温TW=1413 K[12]。几何模型及轴对称流场计算域如图4所示。

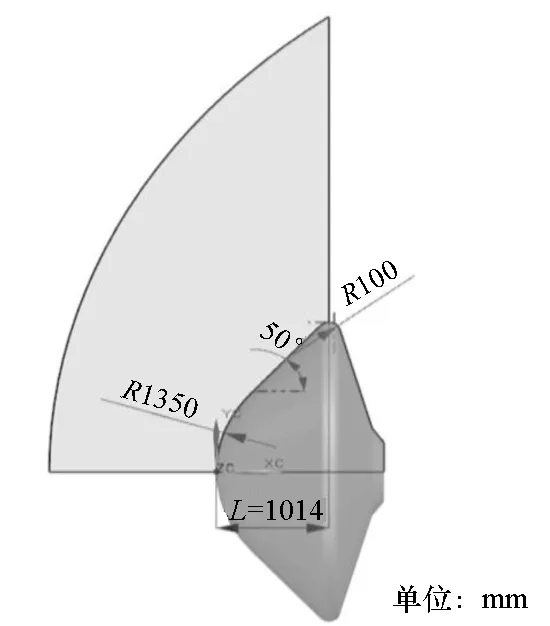
图4　OREX外形及轴对称流场计算域Fig.4　Configuration of OREX and calculation region

为分析常规圆柱螺线管有效工作的磁感应强度范围，设计以下算例：螺线管中心坐标zC=0.80 m，螺线管半径rM=0.60 m，螺线管半长bM=0.18 m，驻点磁感应强度B0=0.05～0.30 T。

4热防护效果分析

图5和图6分别对比了有无外加磁场条件下的驻点线温度和表面热流分布。可以看出，随着B0的增加，激波脱体距离呈正比增加，但驻点区温度峰值保持不变；而表面热流逐渐降低，但降低幅度减小，出现磁控热防护“饱和现象”，这和Bityurin的磁偶极子模型下的结果一致[9]，同样验证了本文数值方法的正确性。

图5　驻点线温度分布Fig.5　Temperature isolines under different B0

图6　不同磁感应强度下的表面热流分布Fig.6　Heat flux under different B0

图7和图8分别对比了B0=0.30 T和B0=0.05 T时的洛伦兹力和温度分布。结合原理图1可以看出，常规螺线管磁铁在返回舱肩部附近产生的周向感应电流方向和头部驻点区的相反，洛伦兹力继续对流体进行减速。相对于B0=0.05 T，B0=0.30 T时肩部洛伦兹力从接近0 N增加到了约800 N，对肩部流体开始有明显的减速作用，甚至出现流动分离与再附，再附点温度增加，在图6中有所体现。可见，对于OREX，采用常规螺线管磁控系统时，过度增加磁感应强度会使得肩部热防护情况恶化；磁场强度存在最优值，应根据防热需求进行优化选择。

图7　洛伦兹力分布对比Fig.7　Comparison of Lorentz force

图8　温度等值线分布对比Fig.8　Comparison of temperature isolines

表1给出了常规螺线管的磁控效果。和图5一致，激波脱体距离随B0呈正比增加；在一定的驻点磁感应强度范围内(B0≤0.20 T)，驻点热流和总热流随B0的增加迅速降低，之后，驻点热流和总热流变化缓慢，出现磁控热防护“饱和现象”。考虑到B0从0.20 T增加到0.25 T过程中电能消耗增加较多(↑25%)，常规螺线管磁控系统可取的工作驻点磁感应强度范围为0.05～0.20 T。当B0=0.20 T时，驻点热流密度和总热流分别降低了31.3%和56.6%，热防护效果显著。前文提到的B0=0.30 T时肩部热环境恶化的现象在这里也有所体现，相对于B0=0.25 T，总热流反而有所提高。

表1　常规螺线管的磁控效果

5工程可行性分析

从驻点磁感应强度、导线工作电流密度和长度三个角度分析螺线管磁控系统的半径、长度和安装位置的设计要求。

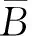
(7)

由上节分析可知，常规螺线管磁控系统可行的驻点磁感应强度范围是0.05～0.20 T。从式(2)中，B0和I(电流密度Jcoil)的正比关系，可知B0=0.05 T所需的导线电流密度应为B0=0.20 T时的1/4，即2.5 A/mm2以下。图9给出了不同螺线管半径下达到B0=0.05 T所需励磁电流密度和导线长度Lcoil值，其中螺线管半长bM=0.24 m。由图可以看出，随着螺线管半径的增加，达到驻点磁感应强度B0=0.05 T所需的导线电流密度逐渐减小，但所需的导线长度逐渐增加；螺线管中心越靠近驻点，所需的导线电流密度越小。当zC<0.8 m并且rM>0.6 m时，达到驻点0.05 T磁感应强度所需电流密度在2.5 A/mm2左右。因此，为满足Jcoil<2.5 A/mm2的要求，同时降低导线质量，可以取rM≈0.6 m。从图10同样可以看出，随着螺线管长度的增加，导线电流密度逐渐减小而导线长度逐渐增加，此时可取bM≈0.24 m。

图9　不同螺线管半径下B0=0.05 T所需励磁电流密度以及导线长度(bM=0.24 m)Fig.9　Required current density and coil length while B0 equals 0.05 T under different rM(bM=0.24 m)

图10　不同螺线管半长下B0=0.05 T所需励磁电流密度以及导线长度(rM=0.6 m)Fig.10　Required current density and coil length while B0 equals 0.05 T under different bM(rM=0.6 m)

尽管缩短螺线管和驻点距离可以有效降低所需的导线电流和长度，但是该距离会受到飞行器鼻锥曲面构型以及螺线管圆柱构型不匹配的限制。此外，过度缩短该距离，会使得肩部热防护环境恶化。所以，应采用可缩短与驻点间距离的异形螺旋管或超导磁铁等替代方法来满足工程防热需求。

6结论

由于存在磁控热防护“饱和现象”，常规螺线管磁控系统的较优工作条件为B0在0.05～0.20 T范围内；相比无磁控防护，B0=0.20 T时，驻点热流和总热流分别降低了31.3%和56.6%，防热效果显著。

对于OREX飞行器，当螺线管中心和驻点距离zC=0.8 m时，过度增加磁感应强度会使得肩部热防护情况恶化，导致表面总热流增加。

在磁控热防护系统的较优工作范围内，为不超过电流密度上限，螺线管中心与驻点间的距离需满足zC≤0.8 m；结合降低导线质量的要求，可取螺线管半径rM≈0.6 m，半长bM≈0.24 m。尽管如此，常规通电螺线管磁控系统导线质量仍然较重，应采用可缩短与驻点间距离的异形螺旋管或超导磁铁等替代方法来满足工程防热需求。

参考文献(References)

[1]夏刚, 程文科, 秦子增. 充气式防热罩再入轨道设计[J].国防科技大学学报, 2002, 24(3): 4-9.

XIA Gang, CHENG Wenke, QIN Zizeng. Re-entry trajectory design of inflatable thermal shield[J]. Journal of National University of Defense Technology, 2002, 24(3): 4-9.(in Chinese)

[2]Lu H B, Liu W Q. Thermal protection efficiency of forward-facing cavity and opposing jet combinational configuration [J]. Journal of Thermal Science, 2012, 21(4): 342-347.[3]刘伟强, 聂涛, 孙健, 等. 一种层板式发汗和逆喷组合冷却鼻锥：ZL 201310112295.7[P]. 2015-04-15.

LIU Weiqiang, NIE Tao, SUN Jian, et al. Combined cooling nose with plate perspiration and opposing jet: ZL 201310112295.7[P]. 2015-04-15. (in Chinese)

[4]孙健, 刘伟强. 高超声速飞行器前缘疏导式热防护结构的实验研究[J].物理学报, 2014, 63(9): 094401.

SUN Jian, LIU Weiqiang. Experimental investigation of dredging thermal protection system of hypersonic vehicle leading edge [J]. Acta Physica Sinica, 2014, 63(9): 094401. (in Chinese)

[5]Bisek N J. Numerical study of plasma-assisted aerodynamic control for hypersonic vehicles [D]. USA:The University of Michigan, 2010.

[6]张绍华, 赵华, 杜爱民, 等. “磁阻力伞”三维数值模拟初步结果[J].中国科学:技术科学, 2013, 43(11): 1242-1249.

ZHANG Shaohua, ZHAO Hua, DU Aimin, et al. 3-D numerical calculation of magnetic drag parachute[J].Scientia Sinica Technologica, 2013, 43(11): 1242-1249. (in Chinese)

[7]Gurjanov E P, Harsha P T. AJAX: new directions in hypersonic technology[C]//Proceedings of 27th Plasmadynamics and Lasers Conference, AIAA 1996-4609, 1996.[8]张康平, 丁国昊, 田正雨, 等. 磁流体动力学控制二维扩压器流场数值模拟研究[J].国防科技大学学报, 2009, 31(6): 39-41.

ZHANG Kangping, DING Guohao, TIAN Zhengyu, et al. Numerical simulation of magnetohydrodynamic (MHD) control on 2D diffuser′s flow field [J]. Journal of National University of Defense Technology, 2009, 31(6): 39-41.(in Chinese)

[9]Bityurin V A, Bocharov A N. On efficiency of heat flux mitigation by the magnetic field in MHD re-entry flow[C]//Proceedings of 42nd AIAA Plasmadynamics and Lasers Conference, AIAA 2011-3463, 2011.

[10]Bityurin V A, Bocharov A N. Study of catalytic effects at reentry vehicle [C]//Proceedings of 52nd Aerospace Sciences Meeting, AIAA 2014-1033, 2014.

[11]Bisek N J, Gosse R, Poggie J. Computational study of impregnated ablator for improved magnetohydrodynamic heat shield [J]. Journal of Spacecraft Rockets, 2013, 50(5): 927-935.

[12]Fujino T, Matsumoto Y, Kasahara J, et al. Numerical studies of magnetohydrodynamic flow control considering real wall electrical conductivity[J]. Journal of Spacecraft and Rockets, 2007, 44(3): 625-632.

[13]Cristofolini A, Borghi C A, Neretti G, et al. MHD interaction around a blunt body in a hypersonic unseeded air flow[C]//Proceedings of 18th AIAA/3AF International Space Planes and Hypersonic Systems and Technologies Conference, AIAA 2012-5804, 2012.

[14]Gulhan A, Esser B, Koch U, et al. Experimental verification of heat-flux mitigation by electro-magnetic fields in partially ionized argon flows[J]. Journal of Space and Rockets, 2009, 46(2): 274-283.

[15]雷银照.轴对称线圈磁场计算[M].北京：中国计量出版社, 1991: 65-70.LEI Yinzhao. Axisymmetric coil magnetic field computation[M]. Beijing: China Measurement Press, 1991: 65-70. (in Chinese)[16]Raizer Y P. Gas discharge physics[M]. USA:Springer-Verlag, 1991.

[17]Miller C G Ⅲ. Experimental and predicted heating distributions for biconks at incidence in air at mach 10[R]. NASA-TP-2334, 1984.

[19]李泉凤.电磁场数值计算与电磁铁设计[M].北京：清华大学出版社, 2002: 168-170.

LI Quanfeng. Numerical simulation and design of electro-magnet [M]. Beijing: Tsinghua University Press, 2002: 168-170. (in Chinese)

doi:10.11887/j.cn.201602005

*收稿日期：2015-09-25

基金项目：国家自然科学基金资助项目(90916018)；湖南省自然科学基金资助项目(13JJ2002)

作者简介：李开(1989—)，男，河南开封人，博士研究生，E-mail：LiKai898989@126.com；刘伟强(通信作者)，男，教授，博士，博士生导师，E-mail：liuweiqiang_1103@163.com

中图分类号：V211.1

文献标志码：A

文章编号：1001-2486(2016)02-025-06

Feasibility analysis of solenoid-based magnetohydrodynamic heat shield system for hypersonic vehicles

LI Kai, LIU Weiqiang

(College of Aerospace Science and Engineering, National University of Defense Technology, Changsha 410073, China)

Abstract：In order to analyze the feasibility of MHD (magnetohydrodynamic) heat shield system for the nose cone of hypersonic vehicles, a normal columned solenoid-based MHD thermal protection system model was built. By using the low magneto-Reynolds MHD model, a set of numerical simulations for hypersonic nose cone with external magnetic field were performed; the feasible range of magnetic induction intensity of normal solenoid-based MHD heat shield system was obtained; the requirements of the solenoid's geometric parameters were drawn to meet the limit of coil current density. Results show that, considering the saturation effect and the current density limit existing in the process of MHD thermal protection, the system works better when the stagnation magnetic induction intensity B0 is in the range of 0.05～0.20 T. When B0 is equal to 0.20 T, the stagnation heat flux density and total wall heat flux is reduced by 31.3% and 56.6% respectively, indicating the effectiveness of thermal protection. However, the required coil mass is so heavy that its structure must be optimized to be actually utilized.

Key words：magnetohydrodynamic flow control; hypersonic vehicle; thermal protection; solenoid magnet

http://journal.nudt.edu.cn