飞行器层板式前缘热管防热结构等效热分析*

刘洪鹏，刘伟强

(1.国防科技大学 航天科学与工程学院， 湖南 长沙　410073；2.国防科技大学 高超声速冲压发动机技术重点实验室， 湖南 长沙　410073)



飞行器层板式前缘热管防热结构等效热分析*

刘洪鹏1,2，刘伟强1,2

(1.国防科技大学 航天科学与工程学院， 湖南 长沙410073；2.国防科技大学 高超声速冲压发动机技术重点实验室， 湖南 长沙410073)

摘要：针对高超声速飞行器前缘尖锐部件所面临的严重气动热，提出层板式前缘热管防热结构。为避免前缘热管内复杂的两相传热传质计算，对高温热管蒸汽腔的传热进行了等效导热分析，讨论了蒸汽腔的等效导热系数的计算方法，与常规高温热管试验对比验证了计算方法的准确性。对该结构热防护效果的计算表明，当飞行器在34 km高度以7Ma速度飞行时，以IN718为管壁材料、Na为工质的层板式热管对头部半径为15 mm的前缘结构具有良好的热防护效果。

关键词：热防护；热管；层板；换热系数

高超声速飞行器在高马赫数飞行时，前缘部位受到严重的气动加热，对飞行器的飞行安全构成严重危害[1-4]。高温热管热防护方式利用封闭腔内金属液体的蒸发、流动和冷凝，将前缘头部高热流区的热流疏导至后部区域并辐射到大气环境中，使得前缘构件趋向均温并降低头部最高温度和热应力，是一种可靠性较高并且可重复使用的热防护技术。

提出于20世纪70年代[5]的热管热防护技术，被大量的理论和实验研究证明了其良好的防热效果[6-8]。近年来，随着材料和工艺等技术的发展，几种新型的热管防护结构相继被提出。1992年至2006年，Glass对D型截面热管的前缘构件进行了大量的理论和实验研究，提出了碳/碳-高温热管复合结构[9]；2013年，Kasen采用9方程模型对楔形热管的工作特性进行了工程计算和试验[10]；2014年，Harrison 对楔形构型的Nb-Li前缘热管进行了高温试验，并采用中子图像技术对热管的启动进行了研究[11]。

2014年，孙健等提出一种层板式前缘热管防护结构[12]，对其进行了启动性能的试验研究[13]。刘洪鹏等对该结构的等效导热计算方法进行讨论，并计算该结构的热防护性能。

1层板式前缘热管防热结构

如图1所示，层板式前缘热管防热结构由外层槽道板和内层板构成矩形截面蒸汽腔。层板采用IN718镍基合金材料，工质采用金属钠。布置于内壁的吸液芯采用孔隙率为0.97镍质金属泡沫结构，其有效毛细半径为225 μm，渗透率为7.74×10-9m2[10]。其工作原理如图2所示，金属液体在头部蒸发端相变吸热产生蒸汽，在蒸汽压差作用下蒸汽流向后部冷凝端冷凝放热，冷凝后的液体工质在吸液芯毛细力作用下被输送至蒸发端，形成工质流动的循环。这使得热量从前缘头部向尾部区域进行重新分配，并降低头部的最高温度、减小其热应力。

图1　层板式前缘热管防热结构Fig.1　Schematic drawing of platelet heat-pipe-cooled leading edge structure

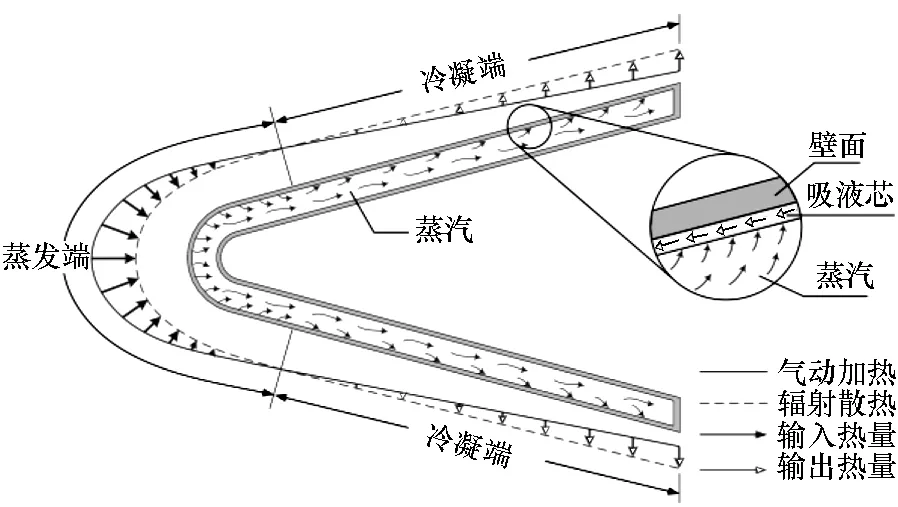
图2　层板式前缘热管防热结构工作原理Fig.2　Schematic diagram of operation of platelet heat-pipe-cooled leading edge

2计算域等效导热系数

热管内的流动和换热情况比较复杂，为方便分析，对热管的物理特性做出如下假设：

①热管处于稳态工作时，不会出现传热极限；②热管内蒸汽为不可压缩流动，轴向温度梯度很小，蒸汽腔具有近似均温性[14]；③蒸汽压差相比于蒸汽腔内的本征压力为很小的量[15]；④热管内蒸汽各处均为饱和状态，蒸汽状态满足饱和蒸汽压力方程。

2.1蒸汽腔等效导热系数

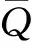
(1)

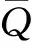
(2)

由饱和蒸汽压方程可知：

(3)

其中，R为蒸汽的气体常数，hfg为工质汽化潜热，TV和PV为蒸汽的饱和温度和压力。

(4)

ΔPV由动量守恒方程进行求解。图3为轴向上，蒸汽域控制体示意图。

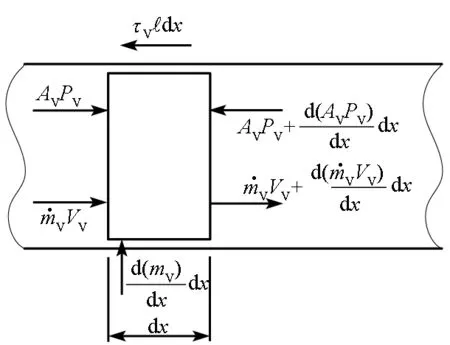
图3　蒸汽腔控制体的动量守恒Fig.3　Control volume for vapor momentum equation

轴向上的动量守恒[15]为：

(5)

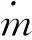
剪应力的计算公式为：

(6)

其中，ρV为蒸汽密度，f为达西摩擦系数。

蒸汽雷诺数ReV可表示为：

(7)

其中：μV为蒸汽的黏性系数；DH为水力直径，其计算公式如式(8)所示。

(8)

将式(6)～(8)代入式(5)可得：

(9)

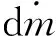
(10)

联立式(1)、式(4)、式(10)可以得到蒸汽腔等效传热系数的计算公式为：

(11)

从式(1)可以看出，蒸汽腔有效导热系数keff,V为蒸汽特定温度下物性参数、蒸汽腔横截面水力直径、蒸汽流动摩擦系数和蒸汽流动雷诺数的关系式。f与ReV的乘积参照文献[16]给出。考虑蒸汽流速为蒸汽传热量Q(x)的函数，蒸汽雷诺数ReV沿轴向的计算公式为：

(12)

2.2吸液芯等效导热系数

基于Peterson[17]的结论，吸液芯结构的有效导热系数keff,W取决于吸液芯的孔隙率、吸液芯和工作液体的导热系数。

(13)

其中：kL和kS分别为工作液和吸液芯金属材料的导热系数，ε为吸液芯结构的孔隙率。

2.3计算方法验证

为了验证有效导热系数计算方法的准确性，将计算结果与Kasen的前缘构型低温稳态试验[10]进行了对比。试验热管的具体参数见文献[10]。试验中，前缘头部的加热功率分别为15 W和25 W，采用热电偶测量了驻点温度，并采用红外热像仪测量热管表面温度。通过图4计算数据与试验数据对比可知，在驻点区域，计算值和热电偶测量值较为吻合，两种工况下其温差均小于2.3%；由红外测温和计算结果可以看出，热管的平面区域呈现出较好的均温性，试验结果和计算结果较为吻合。

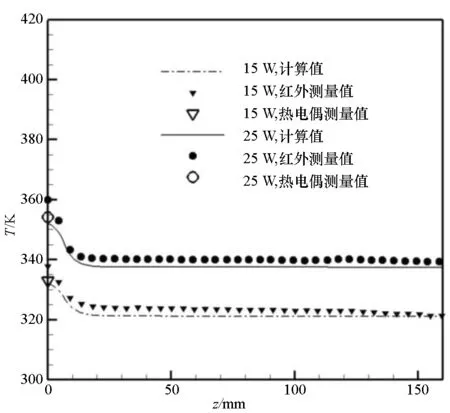
图4　热管壁面温度分布Fig.4　Wall temperature along heat pipe

3防热效果计算

3.1计算模型

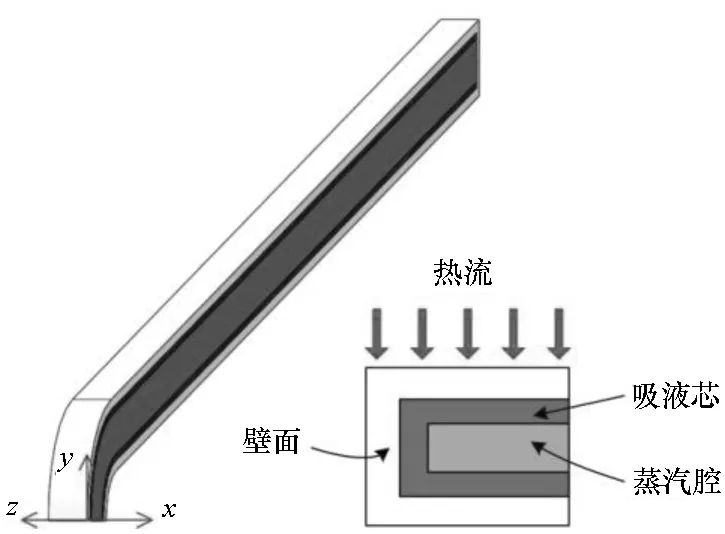
图5　层板式热管计算单元模型简图Fig.5　Schematic diagram of platelet heat-pipe-cooled leading edge

考虑该层板式防热结构中热管分布的周期性和对称性，以单根热管的1/4结构作为计算单元，如图5所示，该结构包括壁面、吸液芯和蒸汽腔三个计算域，其中右下角为热管的横截面简图。前缘外形剖面结构含圆柱段和平直段，其中前缘半楔角为15°，头部半径为15 mm，轴向长度为180 mm，热管壁面厚度为1.2 mm，吸液芯厚度0.7 mm，蒸汽腔宽6.6 mm、高4 mm，相邻热管间距为9.5 mm。

3.2计算方法

基于有效导热系数的理论推导，对层板式前缘热管结构的温度场计算采用纯导热模型。其控制方程为：

(14)

其中，k和T分别为壁面、吸液芯和蒸汽腔不同材料的导热系数和温度。

热管的外壁面有气动加热和辐射两种边界条件。其中气动加热的计算工况为飞行高度34 km，飞行速度7Ma，其气动热值按照文献[18]中的工程计算方法给出。热管计算单元的两侧面和x=0平面均为对称边界。热管的下壁面和后壁面均为绝热边界。

数值计算采用六面体网格，为了有效地捕获前缘头部较大的温度梯度，对该区域进行网格加密。为保证计算的网格无关性，对三种不同的网格大小(流向×法向×展向：180×40×36，360×80×72，720×160×144)进行了计算结果对比，当网格划分由180×40×36提高为360×80×72时，壁面最高温差变化小于0.3%；当进一步提高为720×160×144时，壁面最高温差变化小于0.01%，故对于该计算采用的网格数量为360×80×72。

3.3计算结果

图6　无热防护时温度场分布Fig.6　Without heat pipe cooling

图6和图7为前缘结构的温度场分布。由图6可以看出未采用热管进行热防护时，前缘温度最高尾部温度最低，弦向方向上呈带状分布。由图7可知经过热管的防护后，翼前缘头部温度由1654 K降至1268 K，尾部温度由1013.2 K升至1206.4 K。由于热管高效的传热能力，热量从前缘头部滞止区域疏导至后部平面区域并辐射到外环境中，使得头部最高温度得到大幅度降低，尾部温度得以提高。该层板热管防护结构能够系统地对前缘构件的热量分布进行重新分配，使得前缘构件呈现较好的均温性，有效降低了前缘构件的温度梯度。

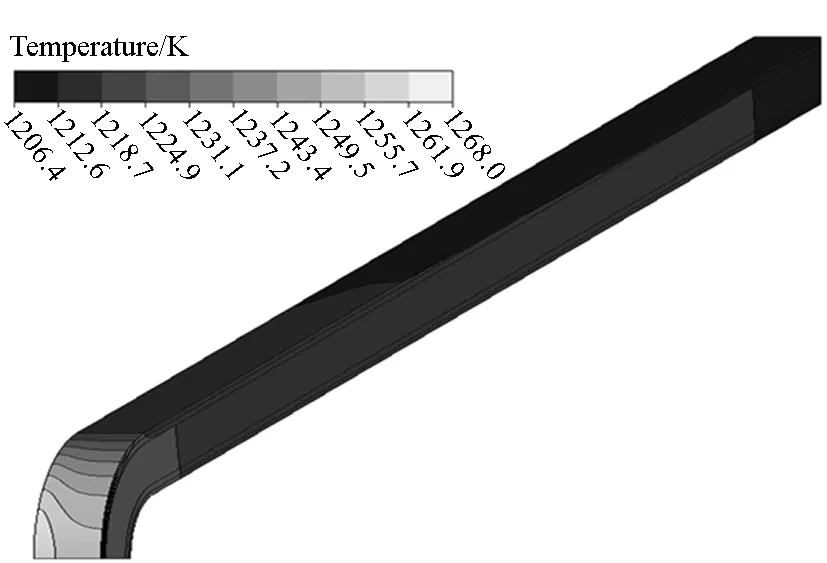
图7　有热防护时温度场分布Fig.7　With heat pipe cooling

4热管极限

热管的传热能力虽然很大，但不能无限地加大热负荷。实际上，热管的传热存在一定的传热极限，其中声速极限、毛细极限与沸腾极限与翼前缘的工作环境相关。虽然对于圆柱形热管的传热极限的研究文献较多[15-17]，但对于前缘热管仍然需要根据其构型进行传热极限分析。

4.1声速极限

当蒸汽的马赫数很高时，尤其是蒸汽流速接近声速时，热管将达到声速极限。声速极限可用式(15)进行计算。

(15)

其中，γ为蒸汽的比热比，对于钠蒸汽，其值为1.67。由于翼前缘所承受的气动热值与前缘构件的半锥角相关，因此可采用简化算法对前缘热管构件的声速极限进行保守计算[10]。

(16)

其中，H为矩形蒸汽腔高度，RLE为前缘头部半径，θ为半锥角。式(16)表明，前缘热管的声速极限主要取决于热管的几何构型和工质的物性参数。

4.2毛细极限

当热管内液体和蒸汽流动的压降之和接近于吸液芯所能提供的最大毛细力时，热管将发生干涸，产生毛细极限，其表达式[15]为：

(17)

其中：σ为工质的表面张力；rc为吸液芯的有效毛细半径；leff为热管的有效长度，对于前缘结构，其值为结构总长度的一半；FL和FV分别为以摩擦系数形式表示的液体和蒸汽压降，其计算方法分别为：

(18)

(19)

其中，μL和μV分别为液体和蒸汽的黏性系数，AW为吸液芯的横截面积，ρL和ρV分别为液体和蒸汽的密度。

4.3沸腾极限

当热管内蒸汽达到临界过热度并且吸液芯内形成稳定的气泡时，热管将发生沸腾极限，其计算可由傅里叶定律推导。

(20)

其中，bW为吸液芯厚度，临界过热度ΔTcrit由式(21)进行计算[15]。

(21)

其中，rb为核态沸腾的气泡半径，可取10-7m。

4.4工作极限

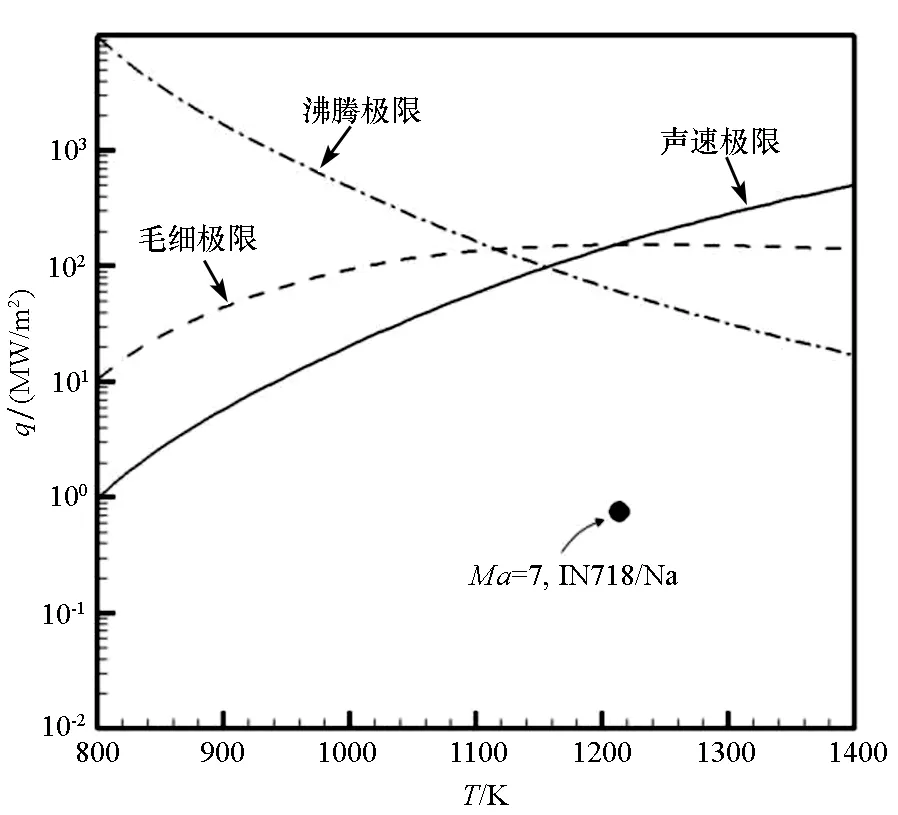
图8　热管工作极限Fig.8　Operating limits for heat pipe

图8中该IN718/Na前缘热管的工作极限随温度的变化，对于采用该镍质金属泡沫结构吸液芯的IN718/Na热管，在800～1400 K工作范围内，其传热上限取决于声速极限和沸腾极限，并且该前缘热管构型可以满足7Ma飞行时的正常工作需求。由热管极限表达式可知，声速极限和沸腾极限取决于前缘热管的几何构型和工质种类。而当前缘构型和工质种类确定时，毛细极限则取决于毛细芯的结构，由于较小的有效毛细半径和较大渗透率的吸液芯可以导致较大的毛细力和较小的液体流动压降，从而具备较大的毛细极限。相比于声速极限和沸腾极限，毛细极限对热管的传热上限的影响，需要针对具体吸液芯结构进行分析和选择。

5结论

1)对蒸汽腔有效导热系数进行了理论推导，为热管冷却效果的快速计算提供了依据。蒸汽腔有效导热系数为蒸汽物性参数、热管截面水力直径和流动状态的函数；

2)层板式前缘热管结构能够有效降低高温区壁面温度，实现了热流从前缘头部向尾部区域的转移，强化了整体构件的热防护能力。

参考文献(References)

[1]夏刚, 程文科, 秦子增. 充气式防热罩再入轨道设计[J].国防科技大学学报, 2002, 24(3): 4-8.

XIA Gang, CHENG Wenke, QIN Zizeng. Re-entry trajectory design of inflatable thermal shield [J]. Journal of National University of Defense Technology, 2002, 24(3): 4-8.(in Chinese)

[2]李道奎， 段静波， 雷勇军. 金属热防护系统瞬态热分析的并联一维模型[J]. 国防科技大学学报, 2009, 31(4): 126-130.

LI Daokui, DUAN Jingbo, LEI Yongjun. Parallel one-dimensional model for transient thermal analysis of metallic thermal protection system [J].Journal of National University of Defense Technology, 2009, 31(4): 126-130.(in Chinese)

[3]张威， 曾明， 肖凌飞， 等. 碳-酚醛材料烧蚀热解对再入流场特性影响的数值计算[J]. 国防科技大学学报, 2014, 36(4): 41-48.

ZHANG Wei, ZENG Ming, XIAO Lingfei, et al. Numerical study for the effects of ablation and pyrolysis on the hypersonic reentry flow [J].Journal of National University of Defense Technology, 2014, 36(4): 41-48. (in Chinese)

[4]李广德， 张长瑞， 胡海峰, 等. 盖板式陶瓷热防护系统的传热性能优化[J].国防科技大学学报, 2014, 36(5): 143-148.

LI Guangde, ZHANG Changrui, HU Haifeng, et al.Optimization study of heat transfer properties for genetic shingle ceramic thermal protection system [J].Journal of National University of Defense Technology, 2014, 36(5): 143-148. (in Chinese)

[5]Silverstein C C.A feasibility study of heat-pipe-cooled leading edges for hypersonic cruise aircraft[R].NASA CR-1857, 1971.

[6]Camarda C J.Aerothermal tests of a heat-pipe-cooled leading edge at Mach 7[R]. NASA TP 1320, 1978.

[7]Boman B, Elias T.Tests on a sodium/hastelloy X wing leading edge heat pipe for hypersonic vehicles[C]//Proceedings of 5th Joint Thermophysics and Heat Transfer Conference, AIAA90-1759, 1990.

[8]Peng W G, He Y R, Wang X Z, et al. Thermal protection mechanism of heat pipe in leading edge under hypersonic conditions [J]. Chinese Journal of Aeronautics, 2015, 28(1): 121-132.

[9]Glass D E.Heat-pipe-cooled leading edges for hypersonic vehicles[R].NASA/CR-2006, 2006.

[10]Kasen S D. Thermal management at hypersonic leading edges[D]. USA:University of Virginia, 2013.

[11]Harrison B. Neutron imaging of lithium (Li) coolants inside high temperature Niobium (Nb) heat pipes[D]. USA: The University of Tennessee, 2014.

[12]刘伟强, 孙健, 聂涛, 等. 一种飞行器的层板式前缘结构: ZL201310311505.5[P]. 2013-12-04.LIU Weiqiang, SUN Jian, NIE Tao, et al. A structure of platelet heat-pipe-cooled leading edge: ZL201310311505.5[P]. 2013-12-04. (in Chinese)

[13]孙健, 刘伟强. 高超声速飞行器前缘疏导式热防护结构的实验研究[J].物理学报, 2014, 63(9): 094401.

SUN Jian, LIU Weiqiang. Experimental investigation of dredging thermal protection system of hypersonic vehicle leading edge[J]. Acta Physica Sinica, 2014, 63(9):094401. (in Chinese)

[14]庄骏, 张红. 热管技术及其工程应用[M]. 北京: 化学工业出版社, 2000.

ZHUANG Jun, ZHANG Hong. Heat pipe technology and engineering application[M]. Beijing: Chemical Industry Press, 2000. (in Chinese)

[15]柴宝华, 杜开文， 卫光仁, 等. 钾热管稳态数值模拟分析[J].原子能科学技术, 2010, 44(5): 553-557.

CHAI Baohua, DU Kaiwen, WEI Guangren, et al. Steady numerical analysis of potassium heat pipe[J]. Atomic Energy Science and Technology, 2010, 44(5):553-557. (in Chinese)

[16]Reay D A, Kew P A, McGlen R J. Heat pipes theory, design and applications[M]. 6th ed. UK: Elsevier′s Science & Technology, 2014.

[17]Peterson G P. An introduction to heat pipes: modeling, testing, and applications[M]. USA:Wiley-Interscience, 1994.

[18]李建林， 唐乾刚， 霍霖， 等. 复杂外形高超声速飞行器气动热快速工程估算[J]. 国防科技大学学报, 2012, 34(6): 89-93.

LI Jianlin, TANG Qiangang, HUO Lin, et al.The rapid engineering earo-heating calculation method for complex shaped hypersonic vehicles[J].Journal of National University of Defense Technology, 2012, 34(6): 89-93. (in Chinese)

doi:10.11887/j.cn.201602004

*收稿日期：2015-10-22

基金项目：国家自然科学基金资助项目(90916018)；湖南省自然科学基金资助项目(13JJ2002)

作者简介：刘洪鹏(1980—)，男，辽宁营口人，博士研究生，E-mail：lhp81-1@163.com；刘伟强(通信作者)，男，教授，博士，博士生导师，E-mail：liuweiqiang_1103@163.com

中图分类号：V211.1

文献标志码：A

文章编号：1001-2486(2016)02-019-06

Effective thermal analysis of platelet heat-pipe-cooled leading edge of vehicle

LIU Hongpeng1,2, LIU Weiqiang1,2

(1. College of Aerospace Science and Engineering, National University of Defense Technology, Changsha 410073, China;2. Science and Technology on Scramjet Laboratory, National University of Defense Technology, Changsha 410073, China)

Abstract：A new structure, the platelet heat-pipe-cooled leading edge, was proposed for hypersonic vehicle thermal protection. In order to avoid the challenge of modeling two-phase conjugate heat and mass transfer, an approach of modeling the vapor core as a solid thermal conductor with high conductivity was adopted and the effective vapor thermal conductivity was deduced mathematically. Its effectiveness was validated by comparing the wall temperature against experimental date for a conventional heat pipe. The research result indicates that the nickel based alloy IN718, with sodium as the working fluid, is a feasible combination form Mach 7 with a 15 mm leading edge radius.

Key words：thermal protection; heat pipe; platelet; thermal conductivity

http://journal.nudt.edu.cn