高超声速飞行器边界层外缘参数仿真分析*
2016-07-26孟竹喧张为华
孟竹喧,胡 凡,2,彭 科,张为华,2
(1.国防科技大学 航天科学与工程学院, 湖南 长沙 410073;2.高超声速冲压发动机技术重点实验室, 湖南 长沙 410073)
高超声速飞行器边界层外缘参数仿真分析*
孟竹喧1,胡凡1,2,彭科1,张为华1,2
(1.国防科技大学 航天科学与工程学院, 湖南 长沙410073;2.高超声速冲压发动机技术重点实验室, 湖南 长沙410073)
摘要:以高超声速飞行器为研究对象,构建快速准确计算高超声速飞行器无黏边界层外缘参数的计算方法。拟合空气比热、比热比随温度变化曲线,建立空气属性温度划分准则。基于不同空气属性建立高超声速飞行器边界层外缘参数工程与数值计算模型,采用钝双锥模型,对比分析工程估算、无黏数值及有黏数值计算方法的计算结果。结果表明,0°攻角状态下,基于无黏流场的数值计算与工程估算和有黏数值计算的压强最大差值分别为1.19%和2.39%;10°攻角状态下,最大差值分别为5%和50%;从而证明所提出的无黏数值计算方法明显优于工程计算方法,为进一步快速准确计算高超声速飞行器气动热环境奠定了重要基础。
关键词:高超声速飞行器;比热/比热比;空气属性;无黏流场仿真;边界层外缘参数
高超声速飞行器气动加热物理过程本质为边界层内的复杂传热传质过程,确定边界层外缘参数是实现高超声速飞行器气动热环境快速、准确计算的重要基础。根据普朗特边界层理论,大雷诺数条件下流场边界层很薄,边界层外的流场参数与飞行器无黏外流场参数基本一致,目前发展了两类边界层外缘参数计算方法,一是基于牛顿理论的工程计算方法,二是基于无黏假设的流场数值模拟方法,前者的计算效率优于后者,后者的计算精度则更高。
目前国内外研究主要集中在单纯数值模拟或工程计算,以流场特性结合工程与数值方法的研究并不成熟,难以满足兼顾计算准确性与效率的要求。
高超声速飞行器外流场不同区域温度分布差异较大,空气属性包含量热完全气体、完全气体、平衡气体、非平衡气体四类,目前常采用的量热完全气体假设(即取比热/比热比为常数)在高温环境下失效。根据温度条件确定空气属性,准确构建比热/比热比计算模型,进而合理建立空气物性参数计算模型,这对保证边界层外缘参数计算精度至关重要。
本文研究高超声速飞行器边界层外缘参数计算问题。根据温度条件确定空气属性,构建比热/比热比计算模型,建立无黏边界层外缘参数工程计算与数值计算模型,完成算例分析,定量对比二者精度、效率等,研究快速准确确定高速飞行器边界层外缘参数的计算方法,为气动热环境计算提供重要的参数支持。
1边界层外缘参数计算模型
1.1空气属性分类与比热/比热比计算模型
Anderson对气体模型划分的定义为[1-3]:完全气体包括量热完全气体、热完全气体和化学反应完全气体混合物;化学反应完全气体混合物中每一组分都遵从完全气体状态方程,达到化学反应平衡的完全气体称为平衡化学反应完全气体。本文不考虑非平衡气体。
大气主要成分是N2,O2,0.1 MPa下空气中反应发生温度如图1所示。恒压状态条件下,800 K分子振动激发,此时定比热假设失效,应用热完全气体假设模型计算;2500 K时O2开始离解,这时应使用平衡化学反应完全气体模型。气体模型适用温度范围如表1所示。

图1 0.1 MPa条件下空气分子振动激发和O2,N2的离解电离Fig.1 Vibrational excitation of air molecularand the dissociative ionization of O2,N2 at 0.1 MPa

气体模型完全气体量热完全气体热完全气体平衡气体温度范围800K以下800~2500K2500K以上
定容比热Cv、定压比热Cp和比热比γ是热力参数计算的重要基础,研究中普遍采用热完全气体假设计算边界层外缘参数,此假设下比热比均为常数,而化学反应平衡气体中比热比不仅是温度的函数,还与每种组分的分压有关[4],此时直接求解比热比较为困难,文献[4]的附录I中给出的空气热力参数插值表,对定容比热Cv、定压比热Cp和比热比γ作多项式拟合,各拟合系数如表2所示,Cv,Cp单位均为J/(kg·K)。
图2~4给出了三个热力参数随温度的变化。由图可以看出,拟合得到的Cv,Cp和γ与文献中给出的数值吻合较好,且变化趋势与空气随温度变化特性十分一致,能够很好地满足热力参数计算需要。

表2 比热/比热比拟合多项式系数

图2 Cv值比较Fig.2 Comparison of Cv

图3 Cp值比较Fig.3 Comparison of Cp

图4 Gamma值比较Fig.4 Comparison of gamma
Cv拟合值与文献[4]给定值最大相差为0.085 6%,Cp最大差值为0.068 3%,γ最大差值为0.060 7%。通过分析可知,本文对气体模型适用温度范围划分与实际吻合良好,各温度范围适于作为气体模型选择标准。
1.2无黏边界层外缘参数计算模型
1.2.1工程计算模型
文献[5]将高超声速流动分为低高超声速区(3.0≤Ma∞≤6.5)和高高超声速区(Ma∞≤8.5),给出了高超声速飞行器压强系数计算方法选择原则,如表3所示。
温度高于800 K时,气体特性不再单纯表征为量热完全气体,计算中普遍采用的正激波前后关系式和等熵关系式不再适用,本文给出不同温度状态下边界层外缘参数工程计算方法,计算流程如图5所示。
对高超声速流场正激波后参数,800 K以下的量热完全气体采用正激波前后关系式可以求解;而对非量热完全气体,Pv=RT仍然成立,但是R在此时是压强P与温度T的函数,通过简单的求解不能求出正激波后参数,需要迭代方法求解。从三大守恒定律和等熵关系出发,将控制方程重新组合后,应用文献[6]中的方法通过一系列迭代求解,得到边界层外缘各参数。
表3高超声速压强系数计算方法
Tab.3Calculation method of hypersonic pressure coefficient
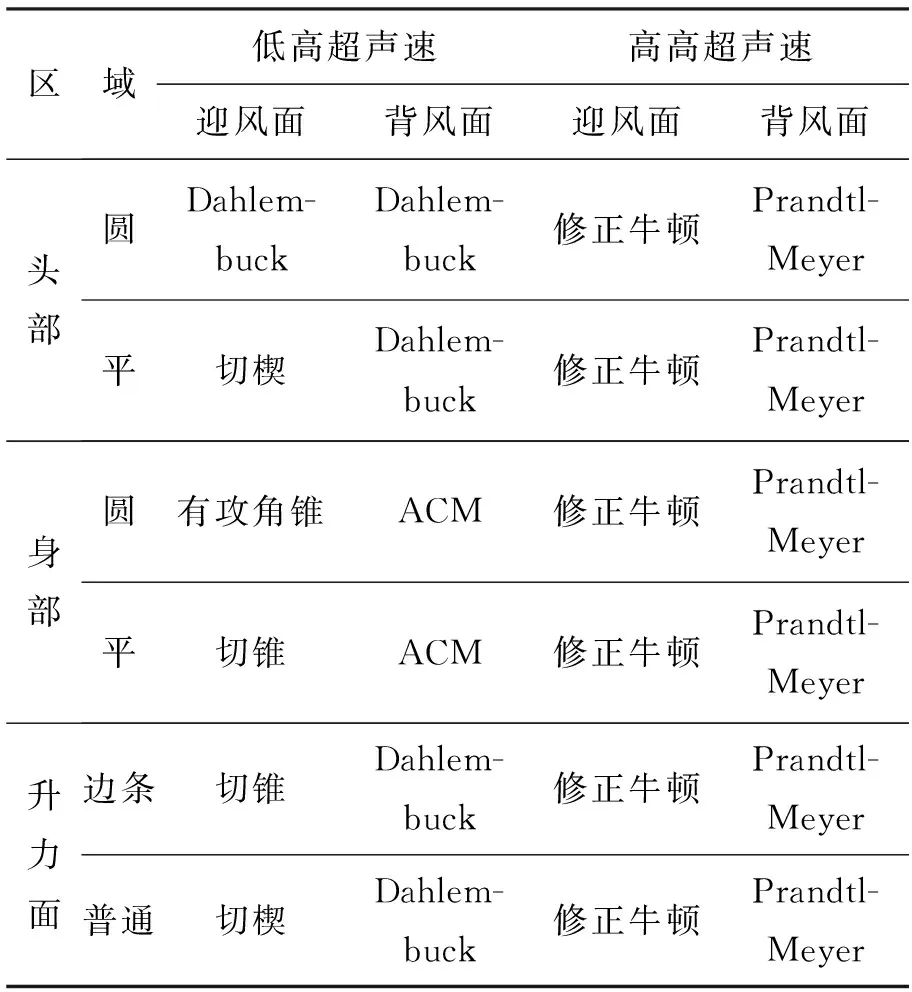
区 域低高超声速高高超声速迎风面背风面迎风面背风面头部圆Dahlem-buckDahlem-buck修正牛顿Prandtl-Meyer平切楔Dahlem-buck修正牛顿Prandtl-Meyer身部圆有攻角锥ACM修正牛顿Prandtl-Meyer平切锥ACM修正牛顿Prandtl-Meyer升力面边条切锥Dahlem-buck修正牛顿Prandtl-Meyer普通切楔Dahlem-buck修正牛顿Prandtl-Meyer

图5 边界层外缘参数工程计算方法流程图Fig.5 Engineering calculation flow-process diagram of outer edge boundary parameters
对于完全气体(包括800 K以下的量热完全气体与800~2500 K的热完全气体两类),焓与内能都只是温度的函数,同时有状态方程Pv=RT成立,且R是常数,这时正激波后压强P2和密度ρ2,利用文献[7]中给出的正激波前后等熵关系式得到边界层外缘密度ρe,由完全气体状态方程求解边界层外缘焓He,由能量方程得到边界层外缘速度Ve,边界层外缘黏性系数μe由萨瑟兰(Sutherland)公式求得。
对实际高超声速流动环境中高于2500 K的平衡气体,由于其复杂的特征,单纯的工程计算很难确切地得到理想结果,所以为了提高热流密度的计算精度,由苏联高温空气动力学函数表拟合的误差不大于10%的流场特性参数计算公式[8]求解得到边界层外缘参数。
1.2.2数值计算模型
边界层外缘参数计算基于无黏欧拉方程如式(1)~(3)所示,采用有限体积法求解;空间离散采用二阶迎风总变差非增(Total Variation Diminishing, TVD)格式,时间推进采用二阶隐式格式[9];为提高计算效率,采用非结构网格划分流场;计算采用平衡气体模型,对于非热完全气体状态下流场同样适用[10]。
连续性方程:
(1)
动量方程:
(2)
能量方程:
(3)
其中:ρ是流场当地密度;u,v,ω分别是当地速度在x,y,z方向的分量;P是当地压强;μ是黏性系数;h是当地焓值。
2边界层外缘参数计算与分析
对于处于平衡状态下的完全气体来说,所有状态参数(例如ρe,ue,Te,SL,Se,Pe)中只有两个是独立的,其他参数均可由热力学关系通过这两个独立变量确定。首先求解边界层外缘压强,以此作为独立变量进一步求解边界层外缘其他五个参数,本节仅给出压强计算结果分布云图。
2.1钝双锥模型边界层外缘参数计算
钝双锥模型是国内外气动热计算相关文献中普遍使用的计算模型,且这一模型在风洞实验中较为常见,拥有详尽的气动热实验数据,本文使用这一模型为后续气动热计算模型验证奠定了基础。钝双锥模型尺寸为:头锥曲率半径为3.835 mm,前锥半锥角为12.84°,后锥半锥角为7°,前锥距头部距离为69.55 mm,后锥距头部距离为122.24 mm[11]。
本文计算了0°,10°攻角状态下,来流P∞=59.92 Pa,T∞=48.88 K,Ma∞=9.86的钝双锥模型边界层外缘无黏流场压强、速度、温度、熵与密度以及流线长度。来流方向为X轴负方向,攻角是在XZ平面内与X轴正方向的夹角。
应用边界层外缘无黏流场工程与数值计算模型对钝双锥模型进行仿真计算,与有黏数值方法计算的迎风面母线压强计算结果进行对比分析。
如图6所示,0°攻角条件下,无黏数值计算得到压强最大值位于头部顶点处,为7.65 kPa;如图7所示,10°攻角条件下,压强最大值位置较0°攻角条件下稍向后移,为7.657 kPa。同样地,由云图可以明显看出,10°攻角条件下,迎风面压强较0°攻角条件下略有增大。
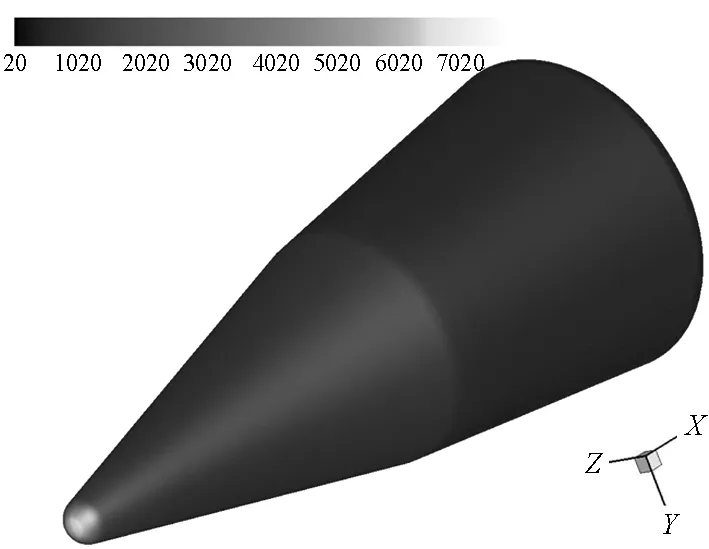
图6 0°攻角无黏数值压强分布云图Fig.6 0° inviscid numerical pressure

图7 10°攻角无黏数值压强分布云图Fig.7 10° inviscid numerical pressure
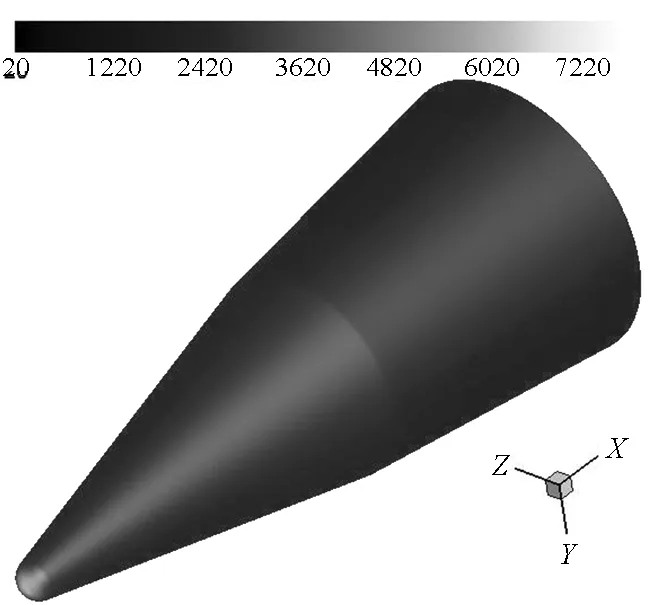
图8 0°攻角有黏数值压强分布云图Fig.8 0° viscid numerical pressure

图9 10°攻角有黏数值压强分布云图Fig.9 10° viscid numerical pressure
如图8所示,0°攻角条件下,有黏数值计算压强最大值位于头部顶点处,为7.734 kPa;如图9所示,10°攻角条件下,压强最大值位于头部顶点稍向后移,为7.620 kPa。相较之前工程计算方法与无黏数值计算方法一样,10°攻角条件下,迎风面压强较0°攻角条件下略有增大。
图10和图11分别给出模型处于0°与10°攻角条件下的边界层外缘无黏流场采用工程计算方法得到的压强分布云图。0°攻角条件下,压强最大值位于头部顶点处,为8.218 kPa;10°攻角条件下,压强最大值仍位于头部顶点处,为8.218 kPa。由云图可以明显看出,10°攻角条件下,迎风面压强较0°攻角条件下略有增大。这与文献中迎风面攻角随攻角增大而增大且迎风面与背风面压强差异随攻角增大而增大的描述吻合。

图10 0°攻角无黏工程压强分布云图Fig.10 0°inviscid engineering pressure

图11 10°攻角无黏工程压强分布云Fig.11 10°inviscid engineering pressure
由上文建模方法计算,可由工程与数值方法分别得出0°和10°攻角状态下边界层外缘无黏流场温度、速度、密度、熵和流线长度的计算结果,在此不一一列出。
2.2计算结果分析
由于本文计算模型缺少实际边界层外缘参数试验数据,本文将考虑黏性的流场数值计算结果作为对比标准,将无黏数值、有黏数值和工程计算结果进行对比分析。
取钝双锥母线上的点,取其距原点长度为X轴变量,以坐标点对应的压强值为Y轴变量作曲线如图12和图13所示。0°攻角状态下工程计算结果和无黏数值计算结果都与有黏数值计算结果吻合较好,工程方法与有黏数值方法结果最大差值为2.39%,无黏数值方法与有黏数值方法最大差值为1.19%。10°攻角状态下,无黏数值计算结果与有黏数值计算结果最大误差不超过5%,而工程计算结果最大误差达到50%。无黏数值方法计算精度优于工程方法。
对比曲线图12和图13可知,无黏数值计算结果整体稍小于有黏数值计算结果,且在飞行器后部差异大于头部。分析误差产生的原因如下:
1)在近壁面区域,考虑黏性的流场相较于无黏流场边界层外缘向外流场稍有扩张,使得空气压缩效应更加剧烈,故无黏数值方法求解的边界层外缘压强较小;
2)有黏流场中流体黏性作用使得飞行器后部流体流速较无黏流场低,由此压强会较无黏流场稍小,离头部位置越远,流体减慢程度越大,则有黏流场与无黏流场计算结果差异越大。
无黏数值计算时间周期以小时为单位,略大于工程计算周期,而有黏流场数值计算周期以天为单位,无黏数值计算效率明显优于有黏数值计算。故在求解飞行器气动热环境计算中,采用无黏数值计算方法求解边界层外缘参数,可以兼顾计算精度与效率。

图12 0°攻角迎风面母线压强对比Fig.12 Comparison of pressure on generatrix of windward at 0°
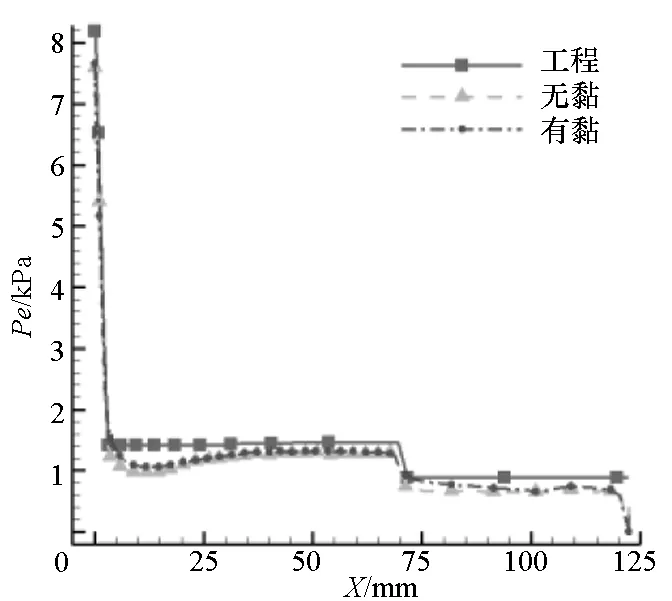
图13 10°攻角迎风面母线压强对比Fig.13 Comparison of pressure on generatrix of windward at 10°
综上分析,所提出的高超声速边界层外缘参数无黏数值求解方法适用于高超声速条件下大雷诺数流场,但在飞行器后部区域稍有误差,计算模型还需通过飞行试验进一步修正。
3结论
1)建立了比热/比热比计算模型,提出了空气属性随温度变化划分准则,为不同温度条件下选择适当无黏边界层外缘参数计算模型奠定了基础;
2)基于温度空气属性划分准则,建立了边界层外缘参数的工程与无黏数值计算模型,以钝双锥模型为对象,求解了其边界层外缘压强、温度、速度、度、熵和流线长度;
3)将钝双锥模型压强无黏数值计算和工程计算结果与有黏计算结果进行对比,无黏数值计算结果的准确性明显优于工程计算结果,计算效率明显优于有黏数值计算,采用无黏数值方法计算边界层外缘参数能够兼顾计算精度与效率,为气动热环境分析提供重要借鉴。
参考文献(References)
[1]Anderson J D. Hypersonic and high temperature gas dynamics[M]. New York: McGraw-Hill Book Company, 1989.
[2]张志成. 高超声速气动热和热防护[M]. 北京: 国防工业出版社, 2003: 1-5.
ZHANG Zhicheng. Hypersonic aerodynamic heat and thermal protection[M]. Beijing: National Defence Industry Press, 2003: 1-5. (in Chinese)
[3]张鲁民. 再入飞船返回舱空气动力学[M]. 北京: 国防工业出版社, 2002.
ZHANG Lumin. Aerodynamics of reentry capsule[M]. Beijing: National Defence Industry Press, 2002. (in Chinese)
[4]徐华舫. 空气动力学基础[M]. 北京: 北京航空学院出版社, 1986.
XU Huafang. Fundamentals of aerodynamics[M]. Beijing: Beijing Aviation Institute Press, 1986. (in Chinese)
[5]Moore M,Williams J. Aerodynamic prediction rationale for analyses of hypersonic configuration[J]. AIAA, 1989.
[6]蒋友娣. 高超声速飞行器气动热和表面瞬态温度计算研究[D]. 上海: 上海交通大学, 2008: 1-4.
JIANG Youdi. Calculation of aerodynamic heating and transient surface temperature for hypersonic aircraft[D]. Shanghai: Shanghai Jiaotong University, 2008: 1-4. (in Chinese)
[7]瞿章华, 曾明, 刘伟, 等. 高超声速空气动力学[M]. 长沙: 国防科技大学出版社, 2001: 1-4.
QU Zhanghua, ZENG Ming, LIU Wei, et al. Hypersonic aerodynamics[M]. Changsha: National University of Defense Technology Press, 2001: 1-4. (in Chinese)
[8]耿艳栋, 肖建军. 关于空天一体化的初步研究[J]. 装备指挥技术学院学报, 2004, 15(6): 19-52.
GENG Yandong, XIAO Jianjun. Preliminary study on air and space integration[J] Journal of the Academy of Equipment Command & Technology, 2004, 15(6): 19-52. (in Chinese)
[9]董维中, 高铁锁. 带座舱飞船高超声速再入非平衡流场的数值研究[J]. 空气动力学学报, 2002, 20(2):239-245.
DONG Weizhong, GAO Tiesuo. Numerical studies of non-equilibrium flow-fields over a capsule-type hypersonic reentry vehicle[J]. Acta Aerodynamica Sinica, 2002, 20(2): 239-245. (in Chinese)
[10]黄志澄. 高超声速飞行器空气动力学[M]. 北京: 国防工业出版社, 1995.
HUANG Zhicheng. Hypersonic aircraft aerodynamics[M]. Beijing: National Defence Industry Press, 1995. (in Chinese)
[11]方磊. 基于流线跟踪法的气动热工程计算研究[D]. 南京: 南京航空航天大学, 2008.
FANG Lei. The study of aerodynamic heating predictions for hypersonic aircrafts based upon tracking the surface streamtrace[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2008. (in Chinese)
doi:10.11887/j.cn.201602006
*收稿日期:2015-02-17
基金项目:国家自然科学基金资助项目(51406230)
作者简介:孟竹喧(1990—),女,吉林白山人,博士研究生,E-mail:m13687361976@163.com;张为华(通信作者),男,教授,博士,博士生导师,E-mail:zwh_kjs@163.com
中图分类号:V411
文献标志码:A
文章编号:1001-2486(2016)02-031-06
Simulation analysis of outer edge boundary parameters for hypersonic-glide vehicle
MENG Zhuxuan1, HU Fan1,2, PENG Ke1, ZHANG Weihua1,2
(1.College of Aerospace Science and Engineering, National University of Defense Technology, Changsha 410073, China;2.Science and Technology on Scramjet Laboratory, Changsha 410073, China)
Abstract:Method of inviscid flow field simulation of the outer edge boundary layer for hypersonic vehicle was created, which was faster than the numerical method and more accurate than the engineering method. And the curve of specific heat and the specific heat ratio changed with temperature were matched, which deduced the law of air attribute on different temperatures. Based on the law, the model of parameters of the outer edge boundary layer for hypersonic vehicle was built, and the comparisons of the results of the proposed method and the engineering method as well as the viscid method of blunt double-cone model were analyzed. Result shows that at the 0° angle of attack, compared with the viscid method, the maximum differences of the pressures between engineering method and viscid method are about 1.19% and 2.39% respectively, while at the 10°angle of attack, they are about 5% and 50% respectively. And the proposed inviscid numerical method obtained higher accuracy is superior to the engineering method, which lays the foundation for the thermal environment calculation of hypersonic-glide vehicle.
Key words:hypersonic vehicles;specific heat and specific heat ratio;air attribute;inviscid flow field simulation;outer edge boundary parameters
http://journal.nudt.edu.cn
