有局部缺陷的滚动体中介轴承动力学建模及仿真研究

徐可君， 董芳华， 秦海勤

(海军航空工程学院 航空机械系(青岛校区)，山东 青岛　266041)



有局部缺陷的滚动体中介轴承动力学建模及仿真研究

徐可君， 董芳华， 秦海勤

(海军航空工程学院 航空机械系(青岛校区)，山东 青岛266041)

摘要：在考虑径向间隙及滚动体缺陷通过内、外圈时接触变形量发生变化基础上，建立两种支承形式下滚动体含单一故障缺陷的中介轴承动力学模型。对比研究不同支承形式及内、外圈不同旋转方向对中介轴承振动影响。结果表明，采用内圈支承于高压转子、外圈支承于低压转子结构振幅大于内圈支承于低压转子、外圈支承于高压转子结构；内、外圈同向旋转振幅大于反向旋转；内、外圈反向旋转冲击振幅小不利于发现故障，反向旋转时缺陷冲击滚道频繁，同等运行条件下，反向旋转中介轴承潜在危险更大；保持架旋转频率为中介轴承振动信号的主要调制频率，且内、外圈反向旋转较同向旋转调制效果更强烈。

关键词：中介轴承；滚动体；局部缺陷；正反旋转；动力学建模

中介轴承能显著缩短转子长度、省却承力框架、降低发动机重量、提高推重比。因此，高性能双/三转子在军、民用航空发动机中广泛采用中介轴承支承结构[1]。与普通轴承相比，中介轴承工作状态更复杂、条件更恶劣，因而故障率亦更突出[2-3]。

对轴承动力特性研究大多集中于普通轴承[4-8]。东亚斌等[9]基于弹性接触理论，考虑故障宽、深度及载荷影响，据内、外圈通过缺陷时释放的接触变形量变化引起弹性接触力变化，建立含单一缺陷的二自由度滚动轴承动力学模型，但保持架不动假设与滚动轴承实际运转不符；另外，设内、外圈通过滚动体缺陷时接触变形量为内、外圈滚道释放的变形量亦存在差异。实际上内、外圈通过缺陷时接触的运动元件均会产生接触变形，总的最大接触变形量应为元件变形量之和(或之差)。

针对中介轴承动力学建模及动力学特性及内、外圈旋转方向不同对轴承动力学特性影响研究较少。本文在以上研究基础上，基于中介轴承两种不同支承形式及内、外圈不同旋转方向，据滚动体缺陷通过内、外圈时接触变形量变化引起弹性接触力变化建立滚动体具有单一局部缺陷的内、外圈径向振动中介轴承动力学模型，并综合考虑轴承径向间隙、滚道及缺陷滚动体变形量影响，改进接触变形模型及滚动体缺陷影响模型。通过数值仿真计算，对比分析不同支承形式及内、外圈不同旋转方向的轴承动力学特性及故障特征量变化。

1含缺陷的滚动体中介轴承动力学建模

1.1中介轴承支承形式

发动机中介轴承支承结构主要有两种形式，即① A型中介轴承支承形式，见图1(a)。其主要特点为轴承外圈支承于低压转子轴颈(随低压转子转动)，内圈支承于高压转子轴颈(随高压转子转动)；② B型中介轴承支承形式，见图1(b)。与A型支承结构相反，B型主要特点为外圈支承于高压转子轴颈(随高压转子转动)，内圈支承于低压转子轴颈 (随低压转子转动)。两种支承形式的内、外圈旋转方向既可同向旋转，亦可反向旋转，具体转向选择取决于发动机的总体及转子结构设计。

图1　中介轴承支承形式Fig.1 Supporting form of intershaft bearing

1.2模型简化及假设

图2　滚动体具有单一局部缺陷中介轴承模型Fig.2 Model of intershaft bearing for local defect rolling element

设接触角为α的中介轴承第j个滚动体存在单一局部缺陷，见图2。图中ωi，ωe分别为轴承内、外圈旋转角速度；Dm为滚动体中心圆直径；φs为滚动体缺陷中心初位角，规定φs值为外圈接触点沿径向顺时针旋转到滚动体缺陷中心的夹角；φj为第j个滚动体t时位置角。

设轴承工作过程中滚动体与滚道间为纯滚动，不存在打滑，并忽略轴承润滑影响等。则保持架旋转角速度ωc及滚动体自转角速度ωb分别为

(1)

(2)

式中：Db为滚动体直径；内、外圈反向旋转取下面符号；同向旋转时取上面符号。

1.3接触变形模型

高速运转的内、外圈在离心力作用下会产生一定径向变形，不可忽略；而径向间隙对轴承刚度及振动特性有重要影响[10]。为便于计算，将内、外圈视为空心圆环，用弹塑性力学理论进行分析[11]，得内、外圈径向变形量分别为uri及ure，则轴承径向间隙改变量为

Δu=ure-uri

(3)

若轴承初始径向间隙为u0，则高速旋转的中介轴承径向间隙为

u=u0+Δu

(4)

此时正常中介轴承第j个滚动体与滚道径向接触变形为

δj=(xe-xi)cosφj+(ye-yi)sinφj-u

(5)

式中：xi，yi分别为内圈中心产生的径向位移在水平、垂直方向投影；xe，ye分别为外圈中心产生的径向位移在水平、垂直方向投影。

据滚动体数目z及第1个滚动体初位角φ1得第j个滚动体t时刻位置角φj为

(6)

1.4滚动体缺陷影响模型

若第j个滚动体存在单一缺陷，则应考虑由缺陷与内、外圈接触所致变形量。设滚动体缺陷与内、外圈接触所致变形量为λ，含单一缺陷滚动体与滚道总径向弹性接触变形为

δj=(xe-xi)cosφj+(ye-yi)sinφj-u-βjλ

(7)

式中：βj为开关量，定义为滚动体缺陷与内圈接触时βj为(-1)2，与外圈接触时βj为1，其它情况βj= 0。具体取值与滚动体缺陷中心位置角(定义φst)及滚动体缺陷跨度角(定义Δφs)密切相关。据滚动体自转角速度ωb，结合图2几何关系，得滚动体缺陷中心位置角φst为

φst=ωbt+φs

(8)

已知φst、Δφs后据中介轴承支承形式及内、外圈旋转方向即可导出滚动体缺陷与内圈或外圈接触时刻。据本文推导有：① 采用A型支承形式，内、外圈同向或反向且内圈顺时针方向旋转；② 采用B型支承形式，内、外圈同向且内圈逆时针方向旋转；③ 采用B型支承形式，内、外圈反向、且内圈顺时针方向旋转。若滚动体缺陷中心初位角φs满足Δφs/2<φs<π-Δφs/2，则βj可表示为

(9)

若滚动体缺陷中心初位角φs满足π+Δφs/2<φs<2π-Δφs/2，则βj可表示为

(10)

而对于：① 采用A型支承形式，内、外圈同向或反向且内圈为逆时针方向旋转；② 采用B型支承形式，内、外圈同向且内圈为顺时针方向旋转；③ 采用B型支承形式，内、外圈反向且内圈为逆时针方向旋转。若滚动体缺陷中心初位角φs满足Δφs/2<φs<π-Δφs/2，则βj可表示为

(11)

若滚动体缺陷中心初位角φs满足π+Δφs/2<φs<2π-Δφs/2，则βj可表示为

(12)

图3　滚动体缺陷通过滚道Fig.3 Defect rolling element passing rings

滚动体缺陷相对滚道位置见图3，图3(a)、(b)为滚动体缺陷通过内圈示意图，图3(c)、(d)为滚动体缺陷通过外圈示意图。设滚动体缺陷宽度为2b，故障深度为d，内圈半径为ri，外圈半径为re。分析图3(a)、(c)可知，滚动体缺陷通过内圈时，若内圈接触到缺陷底部，则其最大接触变形量即为故障深度d；若接触不到，最大接触变形量λmaxi为滚动体变形量Cdr与内圈变形量之和Cdi，即

λmaxi=Cdr+Cdi

(13)

由图3(c)几何关系得

(14)

(15)

同理，分析图3(b)、(d)可知，滚动体缺陷通过外圈时，若外圈接触到缺陷底部，则其最大接触变形量仍为故障深度d；若接触不到，最大接触变形量λmaxe为滚动体变形量与外圈变形量Cde之差，即

λmaxe=Cdr-Cde

(16)

由图3(d)几何关系得

(17)

(18)

式中：j=i,e。

获得总接触变形δj后，据弹性接触理论求得第j个滚动体处接触载荷为

(19)

式中：K为滚动体与滚道等效接触变形系数[12]；对球轴承n=3/2，对圆柱滚子轴承n=10/9。

将所得总接触载荷向X、Y轴投影，则X、Y向总接触载荷为

(20)

1.5运动微分方程

在既定转速下，内、外圈所受偏心力为定值。若已知内、外圈偏心质量me1，mi1及偏心距re，ri，则可据式(21)、(22)求得内、外圈偏心力Fe，Fi为

(21)

(22)

中介轴承采用A型支承形式时，由于内圈随高压转子旋转转速大于外圈随低压转子旋转转速，因此内圈因离心力产生的径向变形量大于外圈，会致滚动体等效弹簧处于受压状态，见图4。由图4看出，将滚动体等效为弹簧阻尼时弹簧为受压状态，内、外圈受大小相等、方向相反的作用力，即内圈会受方向沿其半径指向几何中心的反作用力，外圈受与内圈受力方向相反的作用力。

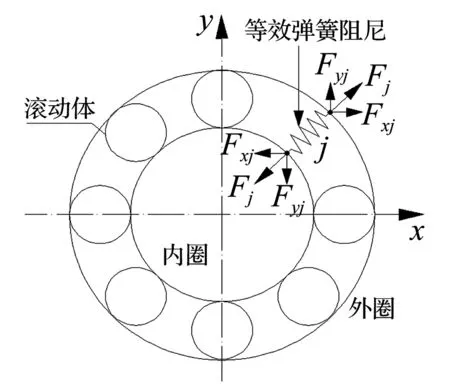
图4　A型支承形式引起的结构受力Fig.4 Structure forces of type a supporting form

由于式(19)中Fj为将滚动体与滚道间接触副视为一组弹簧阻尼模型前提下获得，因此，内、外圈所受第j个滚动体等效弹簧作用力大小即为Fj。所有滚动体产生的总弹簧阻尼力在X、Y轴的投影为Fx、Fy，据牛顿第二定律可得用A型支承形式的中介轴承动力学运动微分方程为

(23)

式中：me为外圈质量；mi为内圈质量；c为等效阻尼；F1为外圈径向外载荷；F2为内圈径向外载荷；Fi，Fe为内、外圈偏心载荷。

同理，据牛顿第二定律可得采用B型支承形式的中介轴承动力学运动微分方程为

(24)

式中：各参数意义同式(23)。

2数值仿真及对比分析

按初始条件对用A支承形式、内外圈同向及反向旋转，且内圈沿顺时针方向旋转的中介轴承进行仿真计算。结果见图5～图8。据式(2)得此时内、外圈同向旋转时保持架旋转频率fc理论值为171 Hz；反向旋转时fc理论值为39 Hz。

分析图6看出，此时内、外圈同向旋转信号频谱结构主要有保持架旋转频率(171 Hz)及其2倍频(342 Hz)、滚动体缺陷冲击滚道特征频率(1 551 Hz)及其2、3倍频(3 103 Hz、4 653 Hz)及保持架旋转所致边频(1 210 Hz、1 893 Hz、2 760 Hz、3 446 Hz)。

图5 内、外圈同向旋转时外圈加速度时域波形Fig.5Accelerationtimedomainwaveformofouterringatco-rotating图6 内、外圈同向旋转时外圈加速度频谱图Fig.6Accelerationspectrumofouterringatco-rotating图7 内、外圈反向旋转时外圈加速度时域波形Fig.7Accelerationtimedomainwaveformofouterringatcounter-rotating

分析图8看出，内、外圈反向旋转信号频谱结构主要有：保持架旋转频率(39 Hz)及其2、3、4倍频(78 Hz、117 Hz、156 Hz)、滚动体缺陷冲击滚道特征频率(5421 Hz)及边频(5 344 Hz、5 500 Hz)；同时出现组合频率fd=fb-20fc≈4 639 Hz及组合频率边频(4 561 Hz、4 716 Hz)。

对比分析图5(a)、(b)与图7(a)、(b)时域波形看出，图5(a)、(b)中量值明显大于图7(a)、(b)量值。说明中介轴承内、外圈同向旋转较反向旋转振动剧烈。而图7(a)、(b)反转的时域波形冲击效应更明显。

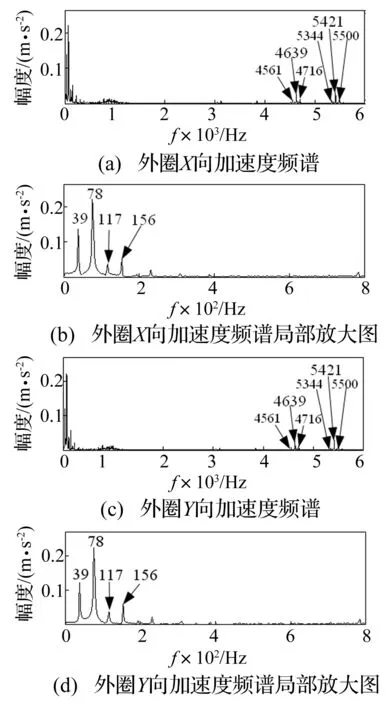
图8　内、外圈反向旋转时外圈加速度频谱图Fig.8 Acceleration spectrum of outer ring at counter-rotating

对B型支承形式，其他仿真参数不变条件下，内、外圈同向、反向，且内圈沿顺时针方向旋转的中介轴承进行仿真，结果见图9～图12。同理据式(2)可得内、外圈同向旋转时fc的理论值为178 Hz，反向旋转时fc理论值为61 Hz。

分析图10看出，此时内、外圈同向旋转且内圈沿顺时针方向旋转的中介轴承，其振动信号频谱结构变复杂化，频谱图中出现调制组合频率fd=fe-fc≈46 Hz及该组合频率导致的保持架旋转频率边频(132 Hz、310 Hz、487 Hz、665 Hz)及滚动体缺陷冲击滚道特征频率(1 551 Hz)及其边频(1 195 Hz、1 373 Hz、1 729 Hz、1 905 Hz)、保持架转频(177 Hz)及其2、3、4倍频(356 Hz、534 Hz、711 Hz)。

分析图12看出，内、外圈反向旋转且内圈沿顺时针方向旋转的中介轴承振动信号频谱主要有：保持架旋转频率(61 Hz)及其2、3、4、5、6、7倍频 (122 Hz、184 Hz、244 Hz、305 Hz、366 Hz、427 Hz)、滚动体缺陷冲击滚道特征频率(5 421 Hz)及其边频(5481 Hz)、组合频率fd=fb-21fc=4 143 Hz及其边频(4 084 Hz、4 205 Hz)。

对比分析图9与图11知，图9(a)、(b)中时域波形量值明显大于图11(a)、(b)。说明对B型支承形式仍为内、外圈同向旋转较正向振动剧烈。

对比分析图5(a)、(b)与图9(a)、(b)及图7(a)、(b)与图11(a)、(b)看出，内、外圈同向旋转时，A型支承形式对应的振动响应值明显大于B型支承形式。说明采用A型支承形式的中介轴承，工作时产生振动更大。原因可能为A型支承形式下中介轴承径向间隙减小，使套圈与滚动体弹性接触力增加，接触变形量增大所致。

图9 内、外圈同向旋转时外圈加速度时域波形Fig.9Accelerationtimedomainwaveformofouterringatco-rotating图10 内、外圈同向旋转时外圈加速度频谱图Fig.10Accelerationspectrumofouterringatco-rotating

图11 内、外圈反向旋转外圈加速度时域波形Fig.11Accelerationtimedomainwaveformofouterringatcounter-rotating图12 内、外圈反向旋转时外圈加速度频谱图Fig.12Accelerationspectrumofouterringatcounter-rotating

比较A、B型支承形式的内、外圈不同旋转方向下振动响应频谱图看出，反转的频谱结构中出现更多阶次的保持架转频，说明内、外圈反向旋转较同向旋转保持架频率对振动信号调制更强烈。原因可能为内、外圈反向旋转时，滚动体缺陷冲击滚道特征频率大，缺陷冲击滚道更频繁所致。

分析表明，滚动体存在缺陷时内、外圈反向旋转的冲击振幅小，不利于发现故障，但反向旋转时缺陷冲击滚道频繁，说明同等运行条件下中介轴承潜在危险更大。

3结论

在建立两种支承形式下、含单一故障缺陷的滚动体中介轴承动力学模型基础上，通过数值仿真对比研究不同支承形式及内、外圈不同旋转方向对中介轴承振动影响，结论如下：

(1) 滚动体存在缺陷时，采用A型支承的中介轴承较采用B型支承振幅大，利于发现故障。

(2) 无论采用何种支承，滚动体存在缺陷时，内、外圈同向旋转均较反向旋转振幅大；而反向旋转冲击振幅小，不利于发现故障，且缺陷冲击滚道频繁，致中介轴承潜在危险增大。

(3) 保持架旋转频率为中介轴承振动信号主要调制频率，且内、外圈反向旋转较同向旋转时调制效果更强烈。

参 考 文 献

[1] 胡绚, 罗贵火, 高德平. 圆柱滚子中介轴承拟静力学分析[J]. 航空动力学报, 2006, 21(6): 1069-1074.

HU Xuan, LUO Gui-huo, GAO De-ping. Quasi static analysis of cylindrical roller intershaft bearing[J]. Journal of Aerospace Power, 2006, 21(6): 1069-1074.

[2] 邓巍,廖明夫,马振国. 航空发动机中介轴承局部故障边带差值诊断法[J].机械科学与技术,2012,31(2):335-339.

DENG Wei, LIAO Ming-fu, MA Zhen-guo. Sideband difference diagnostics of local defects for aero-engine intershaft bearing[J].Mechanical Science and Technology for Aerospace Engineering, 2012,31(2): 335-339.

[3] Sawalhi N, Randall R B. Simulating gear and bearing interactions in the presence of faults part I. the combined gear bearing dynamic model and the simulation of localised bearing faults[J]. Mechanical Systems and Signal Processing, 2008, 22:1924-1951.

[4] Cong Fei-yun, Chen Jin, Dong Guang-ming, et al. Vibration of rolling element bearings in a rotor-bearing system for fault diagnosis[J]. Journal of Sound and Vibration, 2013,332:2081-2097.

[5] Muruganatham B, Sanjith M A, Krishnakumar B, et al. Roller element bearing fault diagnosis using singular spectrum analysis[J]. Mechanical Systems and Signal Processing, 2013,35(1/2): 150-166.

[6] Dong Guang-ming, Chen Jin. Noise resistant time frequency analysis and application in fault diagnosis of rolling element bearings[J]. Mechanical Systems and Signal Processing, 2012 (33): 212-236.

[7] Harsha S P. Nonlinear dynamic response of a balanced rotor supported by rolling element bearings due to radial internal clearance effect[J]. Mechanism and Machine Theory,2006(41): 688-706.

[8] Harsha S P. Nonlinear analysis of a high-speed rotor supported by rolling element bearings[J]. Journal of Sound and Vibration, 2006,290: 65-100.

[9] 东亚斌,廖明夫,高琦. 滚动体具有局部缺陷滚动轴承的动力学分析[J]. 重型机械, 2012(3): 148-152.

DONG Ya-bin, LIAO Ming-fu, GAO Qi. Dynamics analysis on rolling bearing with localized defect[J]. Heavy Machinery, 2012 (3): 148-152.

[10] 袁茹,赵凌燕,王三民. 滚动轴承转子系统的非线性动力学特性分析[J].机械科学与技术,2004,23(10):1175-1177.

YUAN Ru, ZHAO Ling-yan, WANG San-ming. Analysis of the nonlinear dynamic behaviors of a rolling bearing rotor system[J]. Mechanical Science and Technology, 2004,23(10):1175-1177.

[11] 徐秉业,刘信声．应用弹塑性力学[M]．北京，清华大学出版社,1995:184-191.

[12] 邓四二,贾群义,王燕霜. 滚动轴承设计原理[M]. 北京:中国标准出版社, 2008:74-75.

收稿日期：2014-08-12修改稿收到日期：2014-12-31

中图分类号:T，V2

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.02.017

Dynamics modeling and simulation on intershaft bearing with local defect rolling element

XU Ke-jun, DONG Fang-hua, QIN Hai-qin

(School of Naval Aviation Engineering Institute, Department of Aviation Mechanism in Qingdao Branch, Qingdao 266041, China)

Abstract:Considering the radial clearance and the change of contact deformation when a defect rolling element passing through inner and outer rings, the dynamic model of an intershaft bearing with local defect rolling element was established under two kinds of supporting conditions. The effects of different supporting condition and different rotating direction of inner and outer rings on the vibration were comparatively investigated. The results show that the vibration amplitude of the supporting structure with the inner ring mounted on the high-pressure rotor and the outer ring mounted on the low-pressure rotor is bigger than the supporting structure with the inner ring mounted on the low-pressure rotor and the outer ring mounted on the high-pressure rotor. Comparing with the case of counter-rotating of inner and outer rings, the vibration amplitude under the co-rotating of inner and outer rings is bigger. Although the repeated impact amplitude is small and it is not conducive to find fault in the counter-rotating case of inner and outer rings, the rolling element defect attacks the ring groove move frequently, so under the same operating condition, the counter-rotating intershaft bearing has a larger potential risk. The rotating frequency of cage is the main modulation frequency of intershaft bearing vibration signals and compared to the co-rotating case of inner and outer rings, the modulation effect of the counter-rotating inner and outer rings is more intense.

Key words:intershaft bearing; rolling element; local defect; co-rotating and counter-rotating; dynamics model

第一作者 徐可君 男，博士，教授，1963年生

邮箱：xukejunxuran@126.com