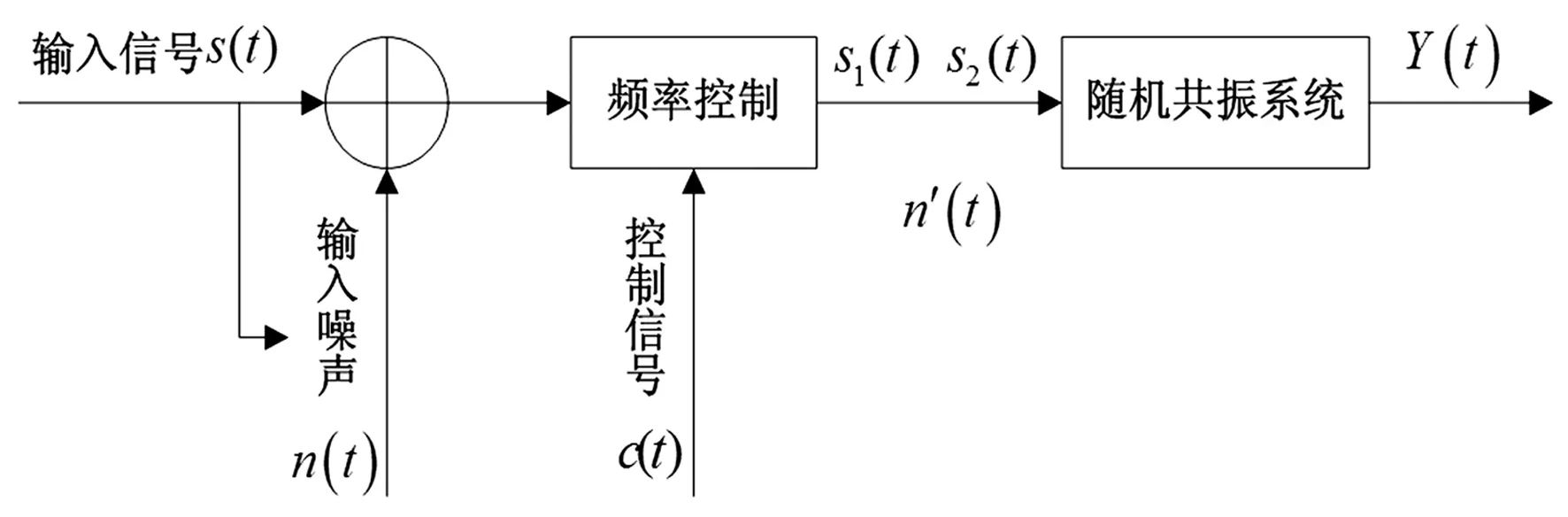
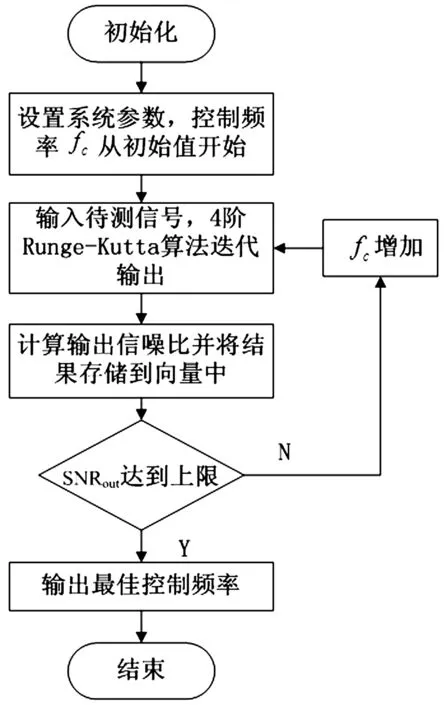
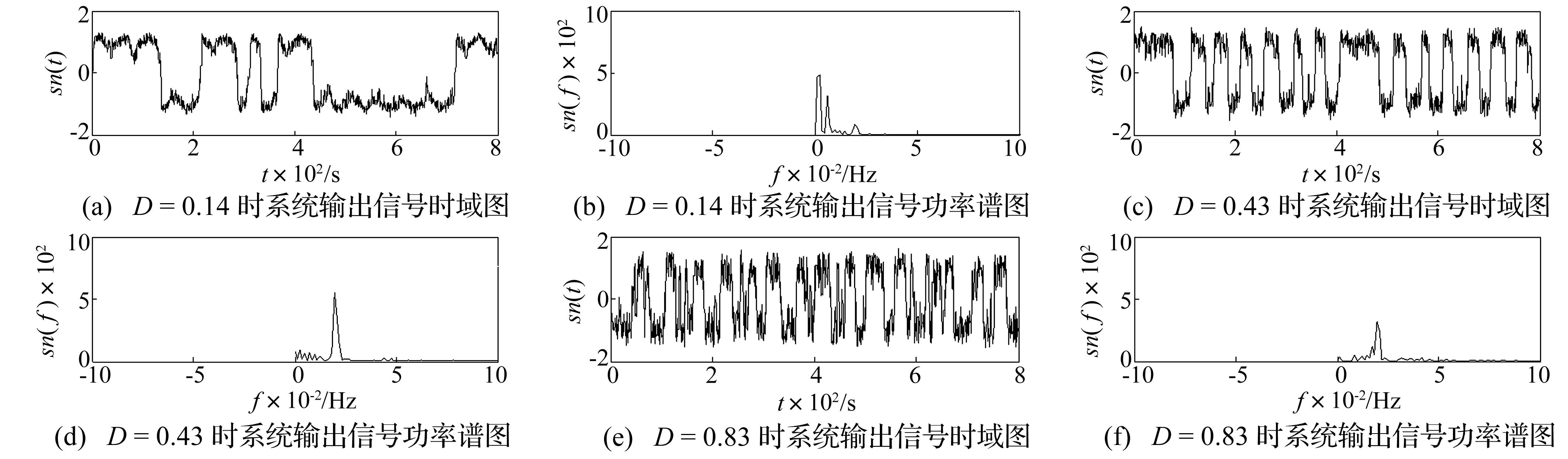
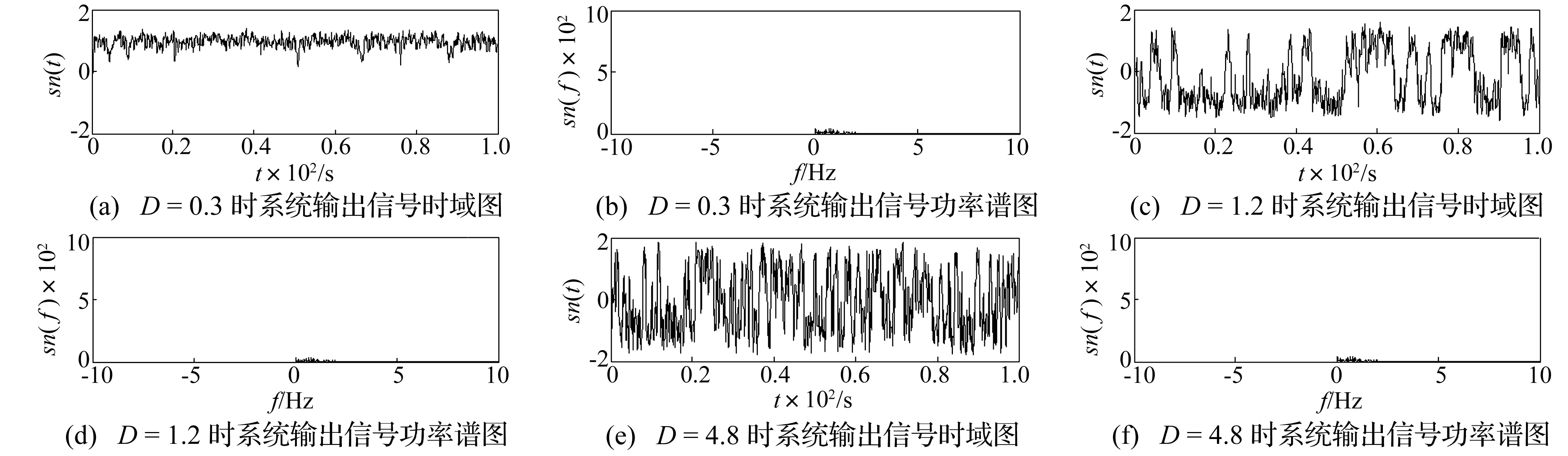
基于频率控制的自适应随机共振系统研究

张　刚， 胡　韬， 张天骐

(1.重庆邮电大学,重庆　400065；2.信号与信息处理重庆市重点实验室，重庆　400065)



基于频率控制的自适应随机共振系统研究

张刚1,2， 胡韬1， 张天骐1,2

(1.重庆邮电大学,重庆400065；2.信号与信息处理重庆市重点实验室，重庆400065)

摘要：研究双稳Duffing系统随机共振产生机理，针对不满足绝热近似条件的大参数信号，提出基于频率控制自适应随机共振微弱信号检测系统，实现对未知大频率微弱信号检测。仿真结果表明，该系统能实现大频率信号随机共振，较传统随机共振系统精度及系统输出信噪比均极大提高，并能扩展其在微弱信号检测领域的应用。

关键词：Duffing系统；频率控制；随机共振；自适应

Benzi等[1-2]研究双稳态模型时首次提出随机共振概念，并利用Budyko-Sellers模型的随机共振解释地球冰川期、暖周期交替现象。该理论获得广泛关注及研究，并提出诸多经典随机共振模型，如阈值系统模型、混沌系统模型、神经系统模型及广义系统模型[3]等。

Duffing振子为微弱信号检测领域中常见的混沌系统模型，为能产生混沌现象的非线性系统，用其敏感性及免疫性能检测强噪声背景的微弱信号效果良好[4-5]，其难点在于原驱动信号的频率设置。对大频率信号，可通过频率尺度变换匹配原驱动信号频率，使待测信号频率与驱动信号频率相同，实现微弱信号检测[6]。本文利用Duffing振子随机共振特性[7]，去除外加策动力信号，将待测微弱周期信号直接作为双稳系统驱动信号实现随机共振；并提出基于频率控制的定步长搜索随机共振系统实现对微弱周期信号检测。

1双稳Duffing随机共振系统特性分析

取一阶非线性系统Langevin方程[8]为

(1)

式中：U(x)为系统势函数；s(t)为外加信号；n(t)为外加噪声。

据非线性系统稳态解个数(曲线U(x)顶点个数)可将稳态随机共振系统分为单稳系统、双稳系统及多稳系统。单稳态系统中，系统只能在平衡点附近的有效区域内运动，即使初始状态远离平衡点，经一定时间振荡后系统将趋于平衡点；而对存在两个稳定点的双稳态系统，会在外力作用下越过势垒点在两稳定点间跃迁。

基于式(1)，构建由周期信号s(t)及噪声信号n(t)共同驱动的二阶Duffing方程为

(2)

式中：k为阻尼比；a>0，b>0为势阱参数。

为方便分析，令s(t)=Acos(ω0t+φ0)，n(t)作为输入信号及噪声，其中信号振幅为A，频率ω0为常数，相位φ0=0，n(t)为均值为0、噪声强度为D的高斯白噪声，满足

〈n(t)〉=0,〈n(t)n(0)〉=2Dδ(t)

(3)

白噪声可表示为

n(t)=σξ(t),σ2=2D

(4)

式中：σ2为噪声方差；ξ(t)为均值0、方差1的高斯白噪声。

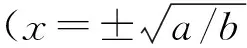
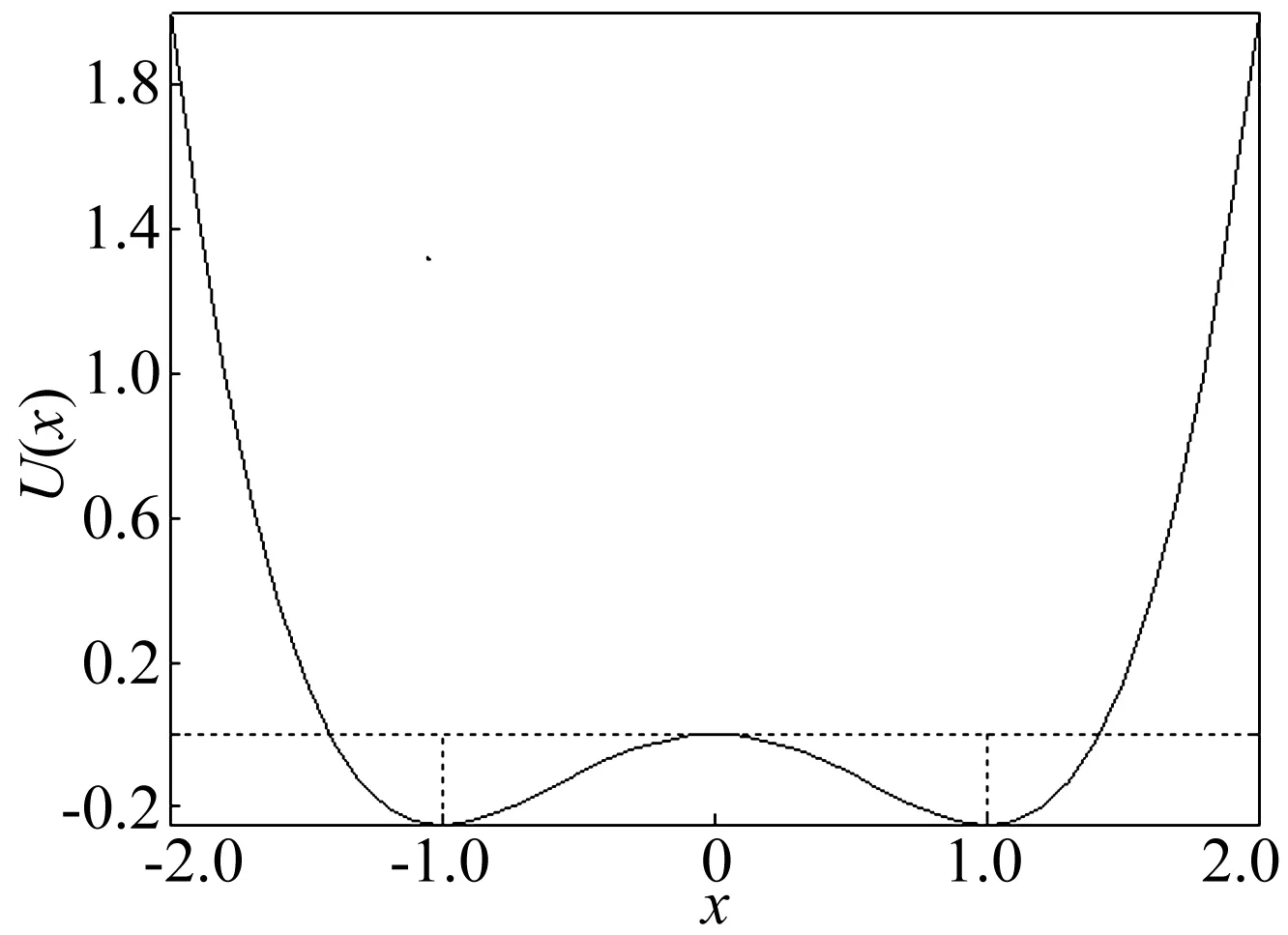
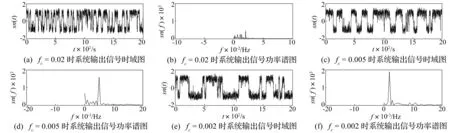
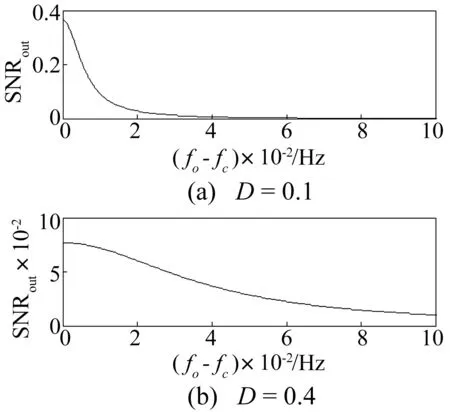
图1　双稳Duffing系统势函数Fig.1 Bistable Duffing system potential function

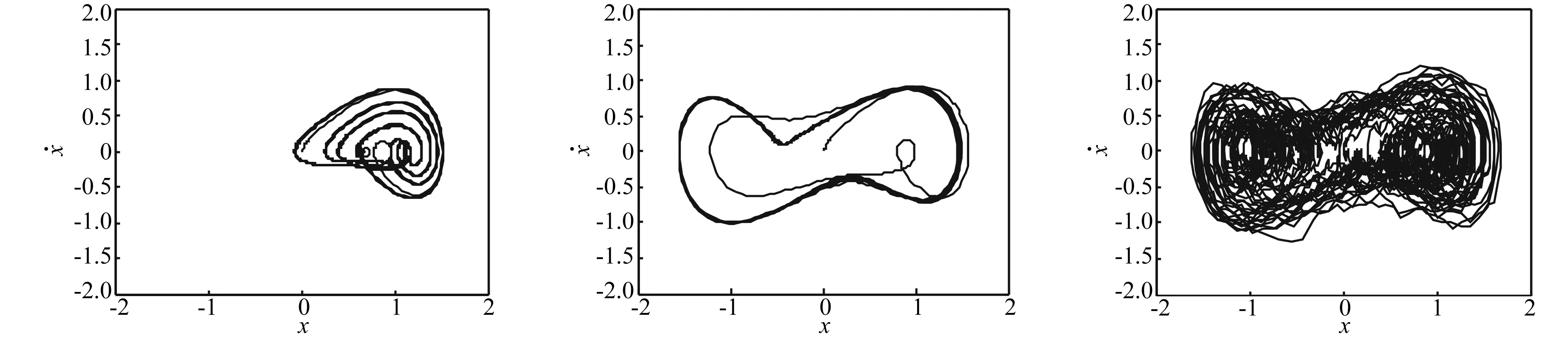
(a) 仅加入周期信号且A

时系统输出越过势垒在两势阱间大范围跃迁运动。此因引入周期策动信号打破系统平衡，使势阱发生周期性倾斜。而系统中同时加入周期正弦信号及噪声时(图2(c))，即使A

2基于绝热近似理论的随机共振

绝热近似理论[9]能较好解释存在于双稳系统中的随机共振现象，即输入信号幅值A、频率ω0及噪声强度D均较小、且三者达到协同效应时，单个势阱内局部平衡可被认为瞬时完成，产生随机共振系统会在两稳态间进行一定概率交换。因此，基于绝热近似理论的随机共振只适用小参数条件(信号幅值A≪1，信号频率ω0≪1，噪声强度D≪1)[10]。

基于此，可得双稳随机共振系统输出功率谱[11]为

(5)

由式(5)看出，输入信号及噪声经非线性双稳系统后，输出信号功率谱Sf0(D,ω)及噪声功率谱Sη(D,ω)均向低频集中，由此亦证明基于绝热近似理论的随机共振只适用低频信号。而现实中需检测的微弱信号大多不满足小参数条件，且频率未知。其中针对大频率微弱信号、未知频率信号最常用方法为对输入信号进行尺度变换(或二次采样)[12-13]及混沌振子阵列法。可见，对任意未知频率微弱信号检测会变困难、复杂。

3基于频率控制的自适应随机共振

3.1频率控制随机共振检测原理

针对频率未知待测微弱信号不能直接输入双稳Duffing系统进行检测问题，提出基于频率控制的自适应随机共振，满足对任意未知频率微弱信号的检测。

信号输入随机共振检测系统前引入频率控制信号对待测微弱信号进行频率调制。先将待测微弱信号与频率控制信号相乘，通过乘法器输出两新的不同频率高、低频信号及统计特性改变的噪声，再将新产生信号及噪声输入随机共振系统。频率控制原理见图3。

图3　频率控制原理Fig.3 The principle diagram of the frequency control

频率控制表达式为

[s(t)+n(t)]c(t)=

[Acos(2πf0t)+n(t)]cos(2πfct)=

n(t)cos(2πfct)=s1(t)+s2(t)+n′(t)

(6)

式中：f1=f0-fc；f2=f0+fc。

由此可知，经频率控制处理后产生具有f1、f2两种新的低、高频成分信号s1(t)及s2(t)，且f1

(7)

(8)

据式(7)可得，经非线性双稳系统后新的频率成分与待测信号频率输出功率关系为

Pf1≥Pf0≥Pf2

(9)

同理，输出噪声能量亦向低频集中，为系统跃迁提供更多能量，一旦输入信号频率与之匹配便能产生随机共振。

3.2基于频率控制自适应算法

由Kramers逃逸率可知，噪声引起的双稳系统在势阱之间的跃迁的速率为

(10)

(11)

当双稳系统参数a=b=1且噪声强度D较大时，由式(11)可求出理论极限值rkmax≈0.225 Hz；系统在某个势阱中的平均驻留时间Tk=1/rk等于周期信号半周期T/2(势函数周期性变化时间)即rk=2f0时，式(2)中Duffing混沌系统将产生随机共振。由此可知，绝热近似条件下双稳系统只能与频率0

以上分析可知，对未知大频率微弱信号，通过引入控制频率fc，总能找到1个新低频信号f1使之满足0

据系统输出信号功率及噪声功率可求出系统输出信噪比表达式为

(12)

将式(11)代入式(12)，得

(13)

通过计算系统输出信噪比大小衡量系统性能，基本流程见图4。具体实施步骤为：① 初始化各系统参数a=b=1，设置控制频率fc步长及搜索范围；②用fc对输入信号进行频率控制，将调制后信号输入非线性双稳系统，用四阶Runge-Kutta算法对非线性微分方程求解；③ 计算系统输出信噪比SNRout并记录，其最大值对应的控制频率即为最优控制频率；④ 将最优控制频率代入系统求解，由f0=f1+fc反算获得待测信号准确频率。

图4　自适应算法流程Fig.4 The adaptive algorithm flow chart

4数值研究与分析

4.1输入信号不经频率控制

4.1.1输入信号为小频率未知信号

由式(2)构建双稳随机共振系统，令系统参数a=b=1，k=0.5，输入信号参数A=0.2 V，f0=0.02 Hz(设输入系统前频率未知)，采样频率fs=5 Hz，噪声强度D分别取0.14,0.43,0.83，采用四阶Runge-Kutta算法对非线性微分方程进行求解，计算点数N=4 096，步长h=0.2。双稳系统输入待测微弱信号为低频信号时，适当增加噪声强度即可使系统克服势垒产生随机共振，见图5。图5(a)、(b)为噪声强度D=0.14时系统输出信号及功率谱，可见因噪声较小，系统未能实现随机共振；由图5(c)、(d)看出，加入适当强度噪声信号时系统、噪声及待测信号有协同效应，致系统产生共振，并在f=0.02 Hz处出现谱峰值特征，表明待测信号频率为f=0.02 Hz。由图5(e)、(f)看出，加入较大强度噪声时系统虽能实现共振并在f=0.02 Hz处出现谱峰值特征，但由于噪声强度过大使系统输出性能下降。由此可见，虽噪声能量可转化为低频信号能量，但不可过度加大噪声强度，只有噪声强度适当才能提高系统的输出性能。

图5　小频率信号在不同噪声强度下系统输出信号时域及功率谱图Fig.5 The system output small frequency signal time domain and power spectrum diagram under different noise intensity

4.1.2输入信号为大频率未知信号

由式(2)构建双稳随机共振系统，令系统参数a=b=1，k=0.5，输入信号参数A=0.1 V，f0=5 Hz(假设输入系统前频率未知)，采样频率fs=20 Hz，噪声强度D分别取0.3,1.2,4.8。采用四阶Runge-Kutta算法对非线性微分方程进行求解，计算点数N=10 000，步长h=0.05。双稳系统中输入待测微弱信号为大频率未知信号时，无论加入多大强度噪声信号，系统均不能实现随机共振，见图6。由图6看出，在3种不同噪声强度下系统均未实现随机共振，且在f=5 Hz处未出现谱峰值特征，由此验证基于绝热近似理论的随机共振只适用小参数条件。

图6　大频率信号在不同噪声强度下系统输出信号时域图和功率谱图Fig.6 The system output big frequency signal time domain and power spectrum diagram under different noise intensity

4.2基于频率控制的自适应未知大频率信号检测

由以上分析知，基于绝热近似理论的随机共振仅适用于小频率信号。大量实验证明，基于频率控制的自适应随机共振可提高系统输出信噪比，达到优化系统性能目的。

由式(2)构建双稳随机共振系统，令系统参数a=b=1，k=0.5，输入信号参数A=0.1 V，f0=30 Hz(设输入系统前未知)，采样频率fs=5 Hz，噪声强度D=0.4。采用四阶Runge-Kutta算法对非线性微分方程进行求解，计算点数N=10 000，步长h=0.2。取控制频率初始值为步长，即fc=0.02，0.005，0.001。按图4步骤搜索待测信号，结果见图7。由图7看出，随控制频率步长减小，系统输出性能得到提升。而当输入信号不经频率控制系统时，则不能产生随机共振，由仿真实验求得此时系统输出信噪比SNRout=0.000 0016，由此可知，非随机共振下信号基本完全被淹没。图7(a) 、(b)为控制频率初始值、步长为0.02时输出信号及功率谱，通过自适应算法搜索，当控制频率fc=29.98 Hz时系统输出信噪比最大且SNRout=0.060 309，在f=0.02 Hz处呈不明显的谱峰值特征，即此时新低频信号f1=0.02 Hz，由f1=f0-fc可计算待测未知大频率信号频率f0=30 Hz；图7(c)～(f)为控制频率初始值、步长为0.005及0.001时输出信号与功率谱，可见控制频率分别为fc=29.995 Hz及fc=29.999 Hz时，系统输出信噪比最大，为SNRout=0.075 431、SNRout=0.076 661。据f1=f0-fc所得待测未知大频率信号频率均为f0=30 Hz，可见，通过提高控制频率精度在一定程度上可改善系统输出性能，输出信号功率明显增加。

图7　大频率信号在不同初始值控制频率时系统输出信号时域图和功率谱图Fig.7 The system output big frequency signal time domain and power spectrum diagram under different initial control frequency

系统输出信噪比SNRout能较好反映双稳系统性能，输入待测频率f0=30 Hz、噪声强度D=0.1、D=0.4时，系统输出信噪比随频率调制的输出新低频信号f0-fc变化曲线见图8。由图8看出，SNRout随f0-fc(控制频率精度)增大性能急剧下降；随噪声强度D增加系统性能进一步恶化。可见，双稳随机共振系统在噪声强度及待测信号频率为低频信号时系统性能更好。因此，利用双稳系统检测待测未知大频率信号时，可通过减小噪声干扰、提高控制频率精度优化系统检测性能。

图8　频率f0=5 Hz时SNRout随f0-fc变化曲线Fig.8 Frequency f0=5 Hz SNRoutwith f0-fc curves

5结论

分析双稳Duffing系统实现随机共振动力学机理，基于绝热近似理论小参数条件基础上提出基于频率控制的自适应算法随机共振系统，结论如下：

(1) 通过频率控制可产生新的小频率信号，并能有效减小噪声干扰。

(2) 基于定步长频率控制自适应随机共振系统，能检测未知大频率信号，可用于未知机械轴承故障信号检测及其它类型微弱周期信号的随机共振检测。

参 考 文 献

[1] Benzi R, Sutera A, Vulpiani A. The mechanism of stochastic resonance[J]. Physics,A, 1981,14: 453-457.

[2] FauveS, Heslot F. Stochastic resonance in a bistable system[J]. Phys. Lett, 1983,97:5-7.

[3] 李月,杨宝俊. 混沌振子检测引论[M].北京：电子工业出版社,2004: 3-25.

[4] 夏均忠,刘远宏,马宗坡,等. 基于调制随机共振的微弱信号检测研究[J] ．振动与冲击,2012,31 (3):133-140．

XIA Jun-zhong,LIU Yuan-hong, MA Zong-po, et al.Weak signal detection based on the modulated stochastic resonance[J]. Journal of Vibration and Shock,2012,31(3): 133-140．

[5] 王娜,郑德忠. 基于混沌振子的低信噪比语音端点检测新方法[J].仪器仪表学报,2009,30 (7):1432-1435．

WANG Na，ZHENG De-zhong. New method for speech endpoint detection under low SNR based on chaotic oscillator[J]．Chinese Journal of Scientific Instrument，2009,30(7): 1432-1435．

[6] 刘海波,吴德伟,金伟,等. Duffing 振子微弱信号检测方法研[J].物理学报, 2013, 62(5):050501.1-050501.6.

LIU Hai-bo,WU De-wei, JIN Wei, et al. Study on weak signal detection method with Duffing oscillators [J]. Acta Physica Sinica, 2013, 62(5):050501.1-050501.6.

[7] 张晓飞,胡茑庆,胡雷,等. 基于倒谱预白化和随机共振的轴承故障增强检测[J].机械工程学报，2012, 48(23): 83-89.

ZHANG Xiao-fei,HU Niao-qing, HU Lei, et al. Enhanced detection of bearing faults based on signal cepstrum pre-whitening and stochastic resonance [J]. Journal of Mechanical Engineering,2012,48(23): 83-89.

[8] He Q B，Wang J．Effects of multiscale noise tuning on stochastic resonance for weak signal detection[J].Digital Signal Processing,2012, 22(4): 614-621．

[9] Gitterman M. Stochastic resonance in a harmonic oscillator with random mass subject to asymmetric dichotomous noise[J]. Journal of Statistical Physics, 2011, 144(1): 139-149.

[10] 韩东颖,丁雪娟,时培明. 基于自适应变尺度频移带通随机共振降噪的EMD多频徵弱信号检测[J].机械工程学报, 2013,49(8):10-18.

HAN Dong-ying,DING Xu-juan,SHI Pei-ming. Multi-frequency weak signal detection based on emd after de-noising by adaptive re-scaling frequency-shifted band-pass stochastic resonance[J]. Journal of Mechanical Engineering,2013,49(8): 10-18.

[11] 胡岗. 随机力与非线性系统[M].上海：上海教育出版社,1994:126-145.

[12] 邓辉,冷永刚,王勇太． 基于XPE的变尺度级联随机共振系统研究[J].仪器仪表学报,2009,30(10):2033-2038．

DENG Hui, LENG Yong-gang, WANG Yong-tai.Study on the scale transformation concatenation stochastic resonance system based on XPE[J].Journal of Scientific Instrument,2009,30(10): 2033-2038．

[13] 冷永刚,赖志慧,范胜波. 二维Duffing振子的大参数随机共振及微弱信号检测研究[J]. 物理学报,2012,63(23):71-80.

LENG Yong-gang, LAI Zhi-hui, FAN Sheng-bo． Large parameter stochastic resonance of two-dimensional Duffing oscillator and its application on weak signal detection[J]． Acta Physica Sinica, 2012, 63(23): 71-80.

基金项目：国家自然科学基金资助项目(61071196;61102131)

收稿日期：2015-05-07修改稿收到日期：2015-07-22

中图分类号:TN911.23

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.02.015

Adaptive stochastic resonance system based on frequency control

ZHANG Gang1,2, HU Tao1, ZHANG Tian-qi1,2

(1. Chongqing University of Posts and Telecommunications, Chongqing 400065, China; 2. Key Laboratory of Signal and Information Processing of Chongqing, Chongqing 400065, China)

Abstract:The stochastic resonance of a bistable Duffing system was studied. Aiming at the large parameter condition which does not meet the adiabatic approximation, a kind of adaptive weak signal detection system with the aid of stochastic resonance based on frequency control was proposed. The system can detect the unknown weak signal with high frequency. The simulation results show that the system can realize the stochastic resonance of high frequency signals. Compared with the traditional stochastic resonance system, its precision and the signal-to-noise ratio of its output are greatly improved, and its application in the weak signal detection field is developed.

Key words:Duffing system; frequency control; stochastic resonance; adaptive

第一作者 张刚 男，博士，副教授，1976年生