基于信息熵与谱有限元法的传感器优化布置

张加培， 尹　涛， 朱宏平， 丁　兰

(1．武汉大学 土木建筑工程学院，武汉　430072；2．华中科技大学 土木工程与力学学院，武汉　430074)



基于信息熵与谱有限元法的传感器优化布置

张加培1,2， 尹涛1， 朱宏平2， 丁兰2

(1．武汉大学 土木建筑工程学院，武汉430072；2．华中科技大学 土木工程与力学学院，武汉430074)

摘要：为从测量数据中获得尽可能多信息，减少待识别模型参数的不确定性，提出面向结构模型参数识别的传感器优化布置方法。为避免用静态形函数传统有限元方法建模对结构动力特性及传感器优化布置影响，采用高精确动力学法即谱有限元法对结构进行动力学建模。以结构模型参数识别结果的不确定性最小作为传感器优化布置准则，该不确定性程度通过信息熵标量指标量化，用贝叶斯统计系统识别法进行识别。采用整数编码遗传算法在所有可能的传感器配置组合中极小化信息熵指标，获得给定数目的传感器最优布置位置。通过弹性地基带弹性接头的周期管梁模型数值仿真及模型试验验证所提方法。

关键词：结构健康监测；传感器优化布置；信息熵；谱有限元法；遗传算法；周期结构

随土木工程的迅猛发展，结构形式日趋复杂，结构健康监测尤其基于振动测量数据的结构健康监测成为重要研究方向[1-2]。该监测方法基于观测的振动数据，而振动数据由传感器采集获得，即传感器个数及其位置决定数据的数量及质量，会直接影响结构健康监测成功与否。显然，测量的信息量越大结构健康监测会越准确，但受测试条件、实际环境及成本所限，不可能无限布置传感器。因此对给定数目传感器，如何布置才能获得尽可能多的信息成为传感器优化布置解决的问题[3]。

目前传感器优化布置方法均基于传统有限元法，但其所用与频率无关的静态形函数求解动力问题尤其频率较高问题时不够精确，会影响传感器优化布置结果[4]。而谱有限元法基于快速傅里叶变换，采用精确波动方程解作为形函数，是传统有限元方法在频域内的表达。理论上，谱有限元法为高精度结构动力学分析方法，用较少数量自由度获得频域的精确解[5]。故本文用谱有限元法对模型进行动力响应分析，并以此为基础进行传感器优化布置研究。

解决传感器最优布置问题，主要有优化布置准则及优化方法两种。目前大多所用优化准则有识别误差最小准则、模态应变能准则、模型缩减法准则、插值拟合准则及可控度可观察度准则等[6]，但对结构健康监测意义不大。Papadimitriou等[7]提出以结构模型参数识别结果不确定性最小为优化布置准则的传感器优化布置方法，实质为通过贝叶斯统计系统识别法计算模型参数的不确定性[8]，用信息熵度量参数估计不确定性大小，信息熵最小时即为参数识别不确定性最小，传感器位置最优。信息熵方法不仅可用于比较不同数目传感器优化布置方案的优劣，且适用于线性、非线性模型识别。尹涛[9]将文献[7]方法推广到分布参数结构，基于连续坐标结构体系进行传感器优化布置问题研究，实现传感器与激励器优化布置。

在传感器所有可能配置组合中快速搜索满足优化准则最优需优化算法实现。理论上该优化问题可用穷举法得到答案。而当结构有大量自由度时仍采用穷举法在所有可能组合中最小化信息熵，效率较低甚至不可行。遗传算法则非常适用此离散优化，故本文基于MATLAB遗传算法工具箱的整数编码遗传算法，针对传感器优化布置问题对遗传算法目标函数进行适当约束[10]，解决传感器最优布置问题。

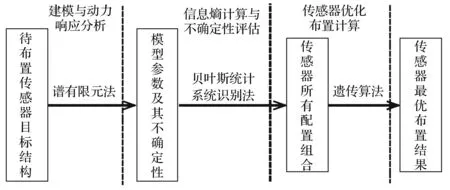
图1　基于信息熵及谱有限元法的传感器优化布置算法流程Fig.1 Procedure of optimal sensor configuration by spectral finite element method and information entropy

本文推广基于信息熵的传感优化布置方法并与谱有限元法结合，形成基于谱有限元法的信息熵指标，采用遗传算法极小化该信息熵指标，进行传感器布置优化问题求解。算法流程见图1。用实验室建立的弹性地基带弹性接头的周期管梁模型数值仿真及实验数据研究，对本文所提方法进行验证。

1理论背景

1.1贝叶斯统计系统识别法

模型参数不确定性可由贝叶斯统计系统识别方法计算获得。设不同模型参数a决定不同模型M，一旦a确定模型M随之确定。对特定模型M(a)，定义q(n;a)∈RNd为模型在所有Nd个自由度上tn=nΔt时刻输出，其中Δt为采样间隔。设在所有Nd个自由度上仅布置N0个传感器，则传感器位置可用向量δ∈RNd表示。当第i个自由度上有传感器时向量元素δi=1，否则为0。因此共有N0个自由度可观察到，系统在tn时刻N0个自由度上输出向量y(n)∈RN0可表示为

y(n)=S0q(n;a)+S0e(n;a)

(1)

式中：e(n;a)为由模型误差、测量噪声产生的预测误差；S0为选择矩阵，每行只有1个等于1的元素，其余全为0。S0中1元素位置由传感器位置向量δ决定。

据贝叶斯统计系统识别理论，待识别参数值及相应不确定性可通过测量动态数据D识别。当J(a)最小时结构模型参数a即为最优值，表示为

(2)

式中：‖·‖为2的范数；N为采样时间点总数。

参数a的不确定性可通过建立概率模型用概率密度函数量化。设模型为线性且预测误差不确定性满足标准正态分布，则a的概率密度函数可由渐近逼近[11]表示为

(3)

式中：c为标准化常数；π(a)为a的先验分布。

1.2信息熵

(4)

(5)

为计算方便，式(5)进一步简化为

(6)

(7)

对两种不同传感器位置向量δ及δ0，H及H0分别为其信息熵，其中δ0可在传感器数量、位置上均与δ不同。由式(4)获得H-H0即信息熵的改变量为

(8)

因此关于传感器位置向量δ及δ0两种不同分布，参数不确定性比值可表示为

(9)

式中：Na为模型参数个数。

由式(9)看出，参数不确定性比值仅依赖于H-H0的改变量及a的数量，该比值可用于度量两种不同传感器配置的参数不确定性改变量。

1.3谱有限元法建模

用弹性地基带弹性接头的周期管梁模型研究传感器优化布置问题。该模型圆管段用梁单元模拟，管间接头仅考虑弯曲变形用转动弹簧kθ模拟。利用弹簧将众多管梁联结形成弹性地基的周期性梁-弹簧模型，见图2。

图2　弹性地基周期管梁模型Fig.2 Periodic pipe-beam model on elastic foundation

考虑Winkler弹性地基，梁的自由弯曲振动方程[12]可表示为

(10)

式中：w(x,t)为横向位移；EI为弯曲刚度；A为梁横截面积；ρ为质量密度；Kf为弹性地基刚度系数。

横向弯矩、剪力分别表示为

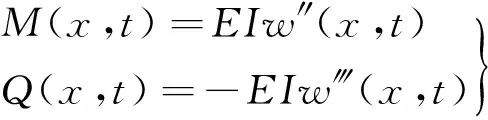
(11)

对式(10)两边进行快速傅里叶变换[13]，频域内梁的平衡方程为

W″″-kFW=0

(12)

式中：W(x,ω)为频域内横向位移；kF为弯曲波数，即

(13)

对长度为L的管梁段，平衡方程通解表达式为

W(x,ω)=a1e-ikFx+a2e-kFx+a3eikFx+a4ekFx(14)

梁单元谱节点位移表达式为

(15)

梁单元谱节点荷载表达式为

(16)

将节点谱位移向量与谱荷载向量写成矩阵相乘形式，即

SB(ω)d=fc(ω)

(17)

式中：SB(ω)为梁的谱单元刚度矩阵，即

(18)

式中：

频域内接头平衡方程为

(20)

式中：kθ为接头弯曲刚度。

接头弹簧单元谱刚度矩阵可表示为

(21)

形成圆管梁与弹簧谱单元刚度阵后，采用与传统有限元法相同步骤，在频域内将所有单元谱单元刚度阵组装成整体刚度阵，将频域内荷载向量组装成整体向量，求解方程组即可获得频域内节点位移，再通过逆傅里叶变换即可获得各节点位移时间历程。

2数值仿真

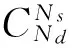
基于MATLAB遗传算法工具箱中整数编码遗传算法求解本文传感器优化布置问题。以整数表示传感器布置，如在9个待测自由度上布置3个传感器，变量[1,5,8]表示第1、5、8自由度位置布置传感器。为避免出现两个及以上数目传感器布置在相同位置，本文在遗传算法的目标函数中增设一不等式约束进行限制。此外，由于遗传算法工具箱中优化函数默认寻求目标函数最小值，当det(Q)取最大值时即表示传感器布置位置最优，因此用-det(Q)作为遗传算法目标函数。遗传算法主要控制参数中再生参数取2，交叉率取0.8，迁移率取0.2。

对弹性地基上通过环间接头连接的周期性管梁模型进行数值仿真研究，模型见图3。共100段梁，每段梁长均为0.5 m，横截面为圆环，模型具体几何、材料参数见表1。考虑本模型弯曲变形显著的结构特性，接头处仅考虑弯曲刚度。仅将管梁接头弯曲刚度作为不确定结构参数进行识别，研究传感器最优布置问题。该模型由99个接头弹簧连接而成，共计99个待识别参数。用系数向量a修正接头弹簧弯曲刚度，即ki=aikθ(i=1,2,…,99)。此外，该模型主要有竖向位移及转角两种变形，但考虑转角测量较困难，仅考虑竖向加速度响应测量。由图3可知，在所有接头处共有99个竖向自由度可供布置传感器。

图3周期管梁模型
Fig.3 Periodic pipe-beam model

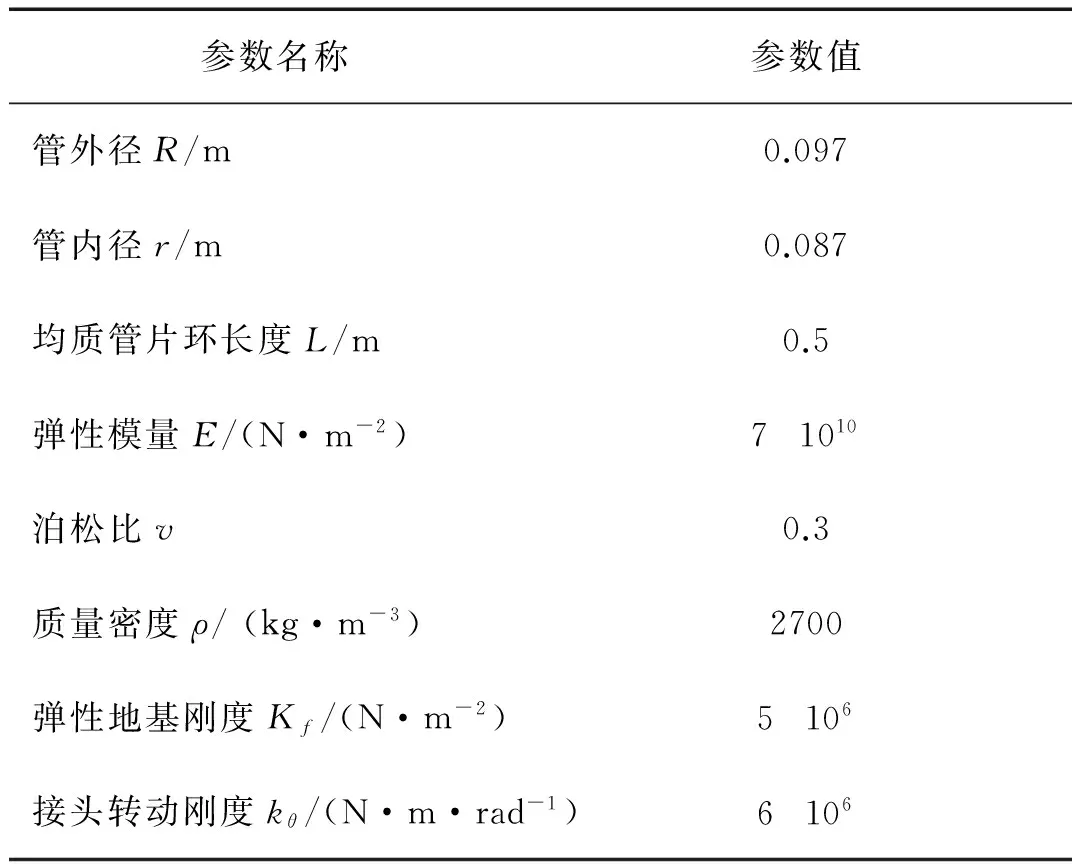
表1　几何及材料参数

基于谱有限元法对模型进行动力学建模，考虑实验时外荷载施加方便，仅在模型左端作用一个竖向冲击荷载。经计算，本模型关心信号最高频率为500 Hz，据采样频率定理，采样频率取1 280 Hz，采样时长为3.2 s，即采样点数N=4 096。

由式(9)知，s/s0可用于度量两种不同传感器配置的不确定性程度改变量，值越小表明参数识别不确性越小。用本文遗传算法进行传感器布置优化计算,获得不同数目传感器最优布置下信息熵s/s0值及具体位置，结果见表2。其中参考值s0对应所有99个自由度均布置传感器情况。由表2看出，在给定传感器数目下，经优化布置的传感器较任意布置能更有效减小模型参数的不确定性，且随优化布置传感器数目增加信息熵随之减小。因此，减小模型参数识别结果的不确定性及从测量数据中获得尽可能多的信息，除单纯增加传感器数量外，需对传感器进行优化布置，以最大限度节省测试成本。本文所提传感器优化布置方法可实现此目的。

表2　信息熵s/s0及最优位置

3实验研究

为进一步验证本文传感器优化方法的正确性，在实验室搭建弹性地基的周期管梁实验模型及测试系统，见图4。该模型几何及材料特性参数与数值仿真相同(表1)。受模型土箱尺寸限制，仅制作5段圆管(图4(a))，由4个环间弹性接头连接各段圆管。与数值仿真类似，仅将各接头弯曲刚度作为结构待识别不确定性参数，即本模型共有4个待识别参数。因竖向位移自由度可测，即所有接头共4个自由度供传感器布置。

实验所用仪器设备为，4个加速度传感器(图4中(b))分别置于4个弹性接头附近，用于测量模型第1～4号自由度竖向加速度响应，由DH5922信号调理采集(图4中(c))，再由装DHDAS动态信号采集分析系统的笔记本电脑记录(图4中(d))，并将数据转存为MATLAB格式用于后续分析计算。本实验模型用冲击力锤在结构左端顶部施加一竖向冲击激励，采样频率、时长及点数均与数值仿真保持一致。

图4　实验系统Fig.4 Experimental system

因仅有4个位置供加速度传感器布置，传感器配置组合较少，尽管采用穷举法可轻易获得所有可能组合的结果，但仍用遗传算法对穷举法结果对比验证。分3种工况，分别对应传感器数目1、2、3，所有可能组合的信息熵s/s0值见表3，其中，参考值s0对应所有4个自由度均布置传感器情况，各测点自由度加速度时程响应见图5。

表3　信息熵s/s0

图5　加速度响应时程曲线Fig.5The measured acceleration time history

由表3看出，改变传感器数目、位置时信息熵随之变化。据本文传感器优化布置准则，信息熵s/s0越小，参数识别不确定性越小，传感器位置更优。据表3结果，传感器数目为2时信息熵s/s0值均小于传感器数目为1时；传感器数目为3时信息熵s/s0值均小于传感器数目为2时。对本模型而言，传感器布置越多，所得信息亦越丰富，参数识别不确定性越小，识别结果越准确。对仅布置单个传感器情况，s/s0最大值为3.27，对应传感器安装在4号自由度，即最差位置。s/s0最小值为2.2，对应传感器置于2号自由度，即传感器最优位置。对2个传感器情况，最优位置为1、2号自由度，而对3个传感器情况，最优位置为1、2、3号自由度。穷举法与遗传算法结果一致，证明本文改进遗传算法的正确性。对本算例而言，传感器数目为N+1的最优位置始终含传感器数目为N的最优位置。

为进一步验证本文传感器优化布置结果，给出第2、4号自由度加速度响应幅值谱，见图6。由图6看出，2号自由度幅值谱出现的峰值数目、大小均较4号幅值谱明显，表明2号自由度频域成分更丰富。而对系统参数识别而言，表示由2号自由度获得数据所含信息量更大，即2号较4号更适合布置传感器。表3中2号自由度信息熵为2.2，4号自由度信息熵为3.27。由于信息熵越小传感器位置越优，故2号优于4号，因此实验与理论计算结果吻合。

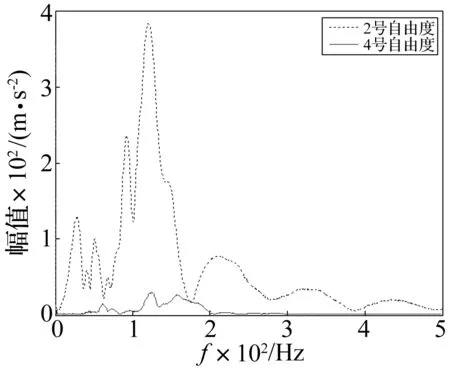
图6　2、4号自由度幅值谱Fig.6 Amplitude spectrum at DOFs 2 and 4

图7　2、3号自由度幅值谱Fig.7 Amplitude spectrum at DOFs 2 and 3

2、3号自由度加速度响应幅值谱见图7。由图7看出，尽管两者频谱曲线无太大区别，但2号自由度频谱曲线所含信息较3号丰富(表现为低频段)，此与表3的理论计算吻合。事实上，2号自由度信息熵比值为2.2，3号自由度信息熵比值为2.24。虽然2号自由度信息熵比值较3号小，但两者数值较接近，由此表明图7中两者频谱图无太大区别原因。尽管如此，3号自由度仍可作为次优位置供传感器布置。

研究结果表明，模型实验与理论计算结果相符，进一步验证本文的基于信息熵与谱有限元法传感器优化布置方法的正确性。

4结论

(1) 提出基于信息熵指标与谱有限元法结合的传感器优化布置方法，并对基于信息熵的传感器优化布置方法进行推广，与谱有限元法结合可避免用静态形函数的传统有限元方法建模对结构动力特性及传感器优化布置影响，形成基于谱有限元法信息熵指标，用以定量评估结构模型参数识别结果的不确定性，并用贝叶斯统计系统识别理论识别该不确定性，将传感器优化布置问题转化为数值优化问题，极小化信息熵指标，进行传感器布置优化问题求解。并通过实验室弹性地基带弹性接头的周期管梁模型数值仿真、实验数据研究，对本文所提方法进行验证。

(2) 通过本文方法优化布置传感器，可有效减少模型参数识别结果不确定性。在给定传感器数目情况下，本文方法可有效增加传感器采集数据中所含与结构模型参数识别有关的信息量，保证待识别模型参数不确定性最小，利于结构健康监测工作开展。本文方法亦可方便地对不同数目、不同位置传感器配置下参数识别结果不确定性程度进行比较，以平衡实际应用中传感器数量(或测试成本)与获取信息量间矛盾，实用性明显。虽仅以弹性地基的周期接头管梁模型进行理论、实验验证，但对其它可用数值建模的一般工程结构均可适用。结构模型规模、复杂程度不同，计算量会有较大差别，即数值模型越复杂待布置传感器位置越多，计算量会越大。

参 考 文 献

[1] 何浩祥,闫维明,张爱林. 面向结构健康监测的传感器数量及位置优化研究[J]. 振动与冲击,2008,27(9)：131-134.

HE Hao-xiang,YAN Wei-ming, ZHANG Ai-lin. Optimization of number and placement of sensors for structural health monitoring[J]. Journal of Vibration and Shock,2008,27(9)：131-134.

[2] 何旭辉,陈政清,黄方林,等. 南京长江大桥安全监测和状态评估的初步研究[J]. 振动与冲击,2003,22(1)：77-80.

HE Xu-hui, CHEN Zheng-qing, HUANG Fang-lin, et al. Preliminary studies on safety monitoring and state assessment for Nanjing Yangtse River Bridge[J]. Journal of Vibration and Shock, 2003, 22(1)：77-80.

[3] Meo M, Zumpano G. Optimal sensor placement on a large scale civil structure[C]//Proceedings of SPIE-The International Society for Optical Engineering, v5394, Health Monitoring and Smart Nondestructive Evaluation of Structural and Biological Systems III, 2004:108-117.

[4] 黄民水,朱宏平,李炜明. 基于改进遗传算法的桥梁结构传感器优化布置[J]. 振动与冲击,2008,27(3)：82-86.

HUANG Min-shui, ZHU Hong-ping, LI Wei-ming. Optimal sensor placement on bridge structure based on genetic algorithm[J]. Journal of Vibration and Shock, 2008, 27(3)：82-86.

[5] LeeU, Kim J, Andrew Y T L. The spectral element method in structural dynamics[J]. The Shock and Vibration, 2000, 32(6): 451-465.

[6] 黄民水,朱宏平,宋金强. 传感器优化布置在桥梁结构模态参数测试中的应用[J]. 公路交通科技,2008,25(2)：85-88.HUANG Min-shui, ZHU Hong-ping, SONG Jin-qiang. Application of optimal sensor placement in modal parameters test of bridge structure[J]. Journal of Highway and Transportation Research and Development, 2008, 25(2)：85-88.[ 7] Papadimitriou C, Beck J L, Au S. Entropy-based optimal sensor location for structural model updating[J]. Journal of Vibration and Control, 2000, 6(5)：781-800.

[8] Beck J L, Katafygiotis L S. Updating models and their uncertainties. I: bayesian statistical framework[J]. Journal of Engineering Mechanics, 1998, 124(4)：455-461.

[9] 尹涛. 一种基于信息熵的分布参数结构传感器/激励器优化布置方法[J]. 振动与冲击,2014,33(22)：51-57.

YIN Tao. A probabilistic approach for optimal sensor/actuator configuration of distributed-parameter systems based on information entropy[J]. Journal of Vibration and Shock, 2014, 33(22)：51-57.

[10] 伊廷华,李宏男,顾明. 基于MATLAB平台的传感器优化布置工具箱的开发及应用[J]. 土木工程学报,2010,43(12)：87-93.YI Ting-hua, LI Hong-nan, GU Ming. Development of MATLAB based optimal sensor placement toolbox and its appliction[J]. Civil Engineering Journal, 2010, 43(12)：87-93.

[11] Chow H M, Lam H F, Yin T, et al. Optimal sensor configuration of a typical transmission tower for the purpose of structural model updating[J]. Structural Control and Health Monitoring, 2011, 18(3): 305-320.

[12] 克拉夫R,彭津J,著.王光远,译.结构动力学[M].北京:高等教育出版社, 2006．

[13] Cho J, Go H, Lee U. Dynamic response of the spectral elment model by using the FFT[J]. Key Engineering Materials, 2007, 345/346：845-848.

[14] 尹涛,余岭,朱宏平. 一种基于模型修正的结构损伤识别方法[J]. 振动与冲击, 2007, 26(6)：59-62.

YIN Tao, YU Ling, ZHU Hong-ping. Model updating based approach for structural damage idenfitication[J]. Journal of Vibration and Shock, 2007, 26(6)：59-62.

[15] 雷英杰,张善文,李续武,等. MATLAB遗传算法工具箱及应用[M]．西安：西安电子科技大学出版社，2005.

[16] 尹涛,朱宏平,余岭. 运用改进的遗传算法进行框架结构损伤检测[J]. 振动工程学报,2006,19(4)：525-531.

YIN Tao, ZHU Hong-ping, YU Ling.Application study of an improved genetic algorithm for frame structure damage detection[J]. Journal of Vibration Engineering, 2006,19(4)：525-531.

基金项目：国家自然科学基金资助项目(51208390)；国家重点基础研究发展 (973)计划资助项目(2011CB013800)；湖北省自然科学基金资助项目(2011CDB265)；中央高校基本科研业务专项经费资助项目(271198, 273766)

收稿日期：2014-08-19修改稿收到日期：2015-01-13

通信作者尹涛 男，博士，副教授，1979年生

中图分类号:O211;O321

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.02.013

Optimal sensor configuration based on spectral finite element method and information entropy

ZHANG Jia-pei1,2, YIN Tao1, ZHU Hong-ping2, DING Lan2

(1. School of Civil and Architectural Engineering, Wuhan University, Wuhan 430072, China;2. School of Civil Engineering and Mechanics, Huazhong University of Science and Technology, Wuhan 430074, China)

Abstract:In structural health monitoring (SHM) based on vibration data, the quantity and quality of the measured data, i.e., the number of sensors and the corresponding locations are very important for the success of SHM utilizing measured dynamic responses. In order to extract the most information from the measured data and reduce the uncertainties of the identified model parameters, a method of optimal sensor configuration for structural model parameters identification was presented. In order to avoid the influence of modeling error induced by traditional finite element method based on static shape function on the results of structural dynamic characteristics and optimal sensor placement, the spectral finite element method, being a dynamic modeling method with high-accuracy, was employed to model the target structure in the proposed method. In addition, the minimum of the uncertainties in model parameter estimates was taken as the optimality criterion for placing sensors, and the information entropy measure was used to quantify these uncertainties which were calculated by the Bayesian statistical identification method. The minimal information entropy measure was drawn from a set of possible sensor configurations to optimally locate a given number of sensors by using an integer-coded genetic algorithm. Both numerical simulation and laboratory experiment were carried out on a periodic pipe-beam model with flexible joints on elastic foundations to verify the effectiveness of the proposed method.

Key words:structural health monitoring; optimal sensor placement; information entropy; spectral finite element method; genetic algorithm; periodic structure

第一作者 张加培 男，硕士生，1989年12月生

邮箱：tyin@whu.edu.cn