考虑身管柔性的坦克行进间发射动力学研究

刘飞飞， 芮筱亭， 于海龙， 张建书， 顾俊杰

(南京理工大学 发射动力学研究所，南京　210094)



考虑身管柔性的坦克行进间发射动力学研究

刘飞飞， 芮筱亭， 于海龙， 张建书， 顾俊杰

(南京理工大学 发射动力学研究所，南京210094)

摘要：针对弹丸起始扰动会影响坦克行进间射击密集度问题，建立身管柔性的坦克行进间发射动力学模型；考虑弹丸动不平衡及质量偏心、弹炮相互作用、弹炮间隙，建立坦克行进间射击弹丸膛内运动方程；编制行进间射击的坦克发射动力学仿真程序，获得某坦克行进间射击弹丸膛内运动规律及千米立靶密集度，并试验验证仿真结果。该结果可为提高坦克行进间射击精度提供理论基础与仿真手段。

关键词：坦克柔性身管；行进间射击；发射动力学；射击精度；弹丸膛内运动

现代战场所用机动战术即为避免敌方弹箭命中的重要手段。作战中既能充分利用机动性能保护自己又能消灭机动之敌，要求坦克具有行进间射击能力及高射击命中精度。理论与试验研究表明[1-2]，弹丸起始扰动为影响武器系统行进间射击精度的主要因素，如路面激励、振动、稳定性等。弹丸发射过程理论为研究弹丸发射的运动规律及起始扰动[3]。非行车发射过程理论已有研究,并取得诸多成果[4-7]。而对坦克行进间发射过程理论[8-10]如弹丸在膛内的运动方程研究尚少。因温度、重力等因素，柔性身管有初始静挠度，发射时弹丸与身管存在的间隙会使二者产生碰撞、摩擦及膛内高压气体对有挠度身管进行矫直等均会使身管产生振动，从而影响弹丸的膛内运动。虽有对身管柔性对弹丸膛内运动影响的研究[11-14]，但因无完善的行进间射击弹丸膛内运动方程，难以精细讨论提高行进间射击精度问题。

因此，本文建立身管柔性的坦克系统动力学模型，考虑弹丸动不平衡及质量偏心、弹炮相互作用及间隙，推导坦克行进间射击弹丸膛内运动方程，以期为提高坦克行进间射击精度奠定理论基础与仿真手段。

1坦克系统发射动力学模型

1.1柔性身管动力学模型

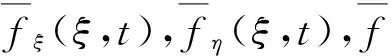
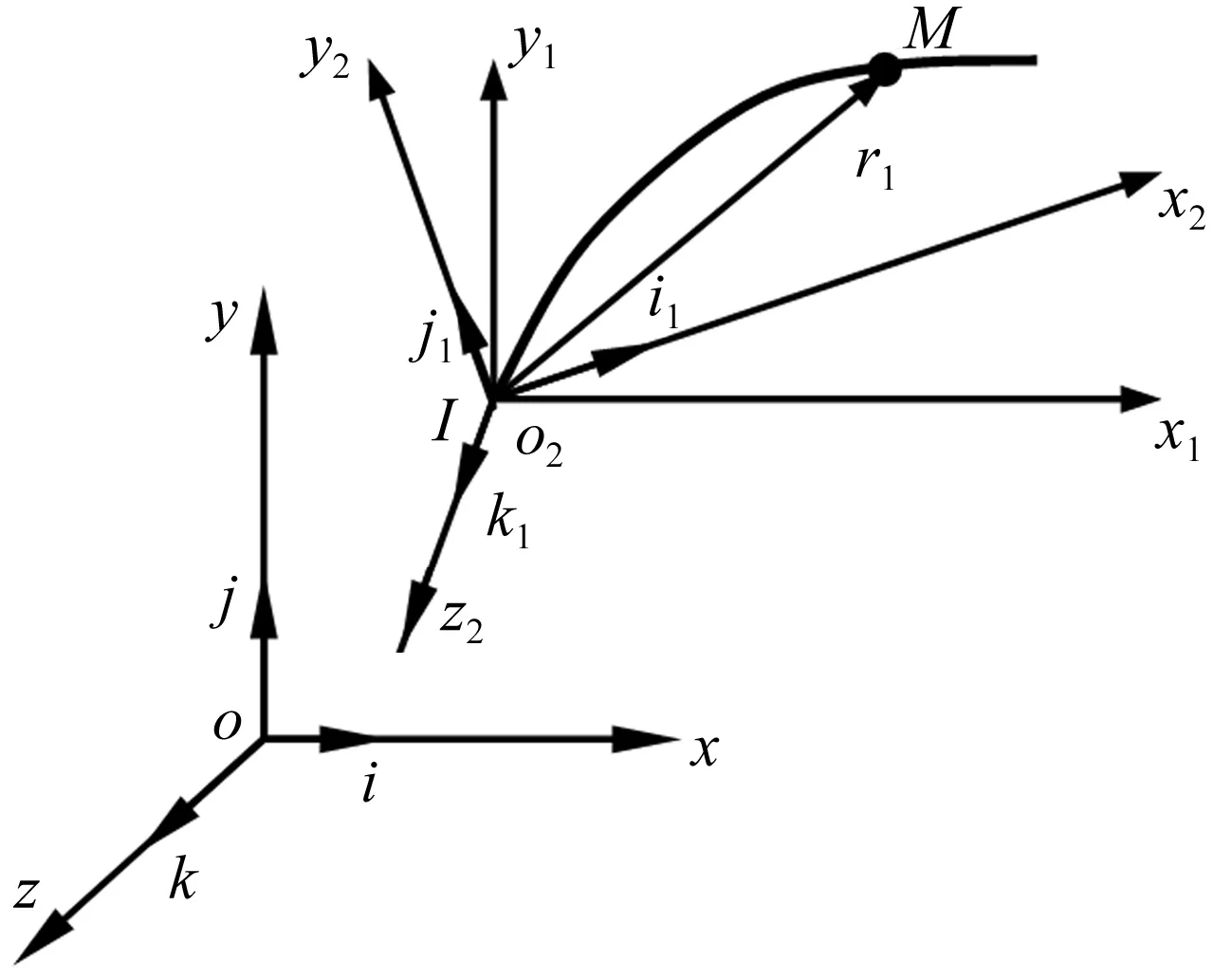
图1　空间运动柔性身管模型Fig.1 Spatial motion flexible barrel

1.2坦克系统发射动力学拓扑模型

现代坦克主要包括火力与发射系统、稳定与控制系统、行走与悬挂系统、发动机与传动系统、通讯及辅助装置等。由上到下依次为身管、炮尾、除后坐部分的起落部分、炮塔、发动机与传动系统、车体、主动轮、平衡肘、诱导轮、负重轮、履带等。据多体系统传递矩阵法，“体”与“体”间的联接统称为“铰”，包括柱铰、滑移铰、弹性铰、阻尼铰等。铰不计质量，其质量全部归入相邻“体”中，并对“体”、“铰”统一编号。摇架前身管部分视为空间弹性梁1；身管其余部分视为刚体3；除后坐部分的起落部分视为刚体5；制退机、复进机质量分别归入起落部分5及身管3，其作用等效为炮尾与起落部分间弹性阻尼铰及后座阻力，炮身与起落部分间相互作用等效为空间柱铰4；炮塔与车体视为刚体7、9；高低瞄准及稳定由作用于起落部分5与炮塔7的控制力Mcθ描述，高低机及起落部分与炮塔的相互作用等效为空间柱铰6；方向瞄准与稳定由作用于炮塔7与车体9的控制力Mcα描述，方向机及车体与炮塔的相互作用由空间柱铰8等效；发动机视为刚体49；发动机与传动系统通过4个支撑与车体作用由4个空间弹性阻尼铰等效，编号为26、27、28、29；主动轮视为刚体33、41；主动轮与车体的联接作用由空间弹性阻尼铰10、18等效；诱导轮视为刚体40、48；诱导轮弹性效应及其与车体的联接作用及张紧装置作用等效为空间弹性阻尼铰17、25；扭杆与减振器质量归入车体，平衡肘视为刚体34、35、…、39，42、43、…、47；平衡肘与扭杆及车体间效应等效为空间弹性阻尼铰11、12、…、16，19、20、…、24；平衡肘与负重轮间效应等效为空间弹性阻尼铰53、54、…、64；12个负重轮视为刚体65、66、…、76；每块履带板视为刚体，履带销质量归入相应履带板，履带板间效应等效为空间弹性阻尼铰，左侧履带板编号为77、79、81、…、239，左侧履带板铰编号为78、80、82、…、240；右侧履带板编号为241、243、245、…、403，右侧履带板铰编号为242、244、246、…、404；3乘员座椅视为刚体50、51、52；各座椅与车体的弹性与阻尼效应等效为空间弹性阻尼铰30、31、32。因此，坦克多体系统发射动力学模型由201个体、203个铰组成的复杂多体系统，发射动力学模型拓扑图见图2。

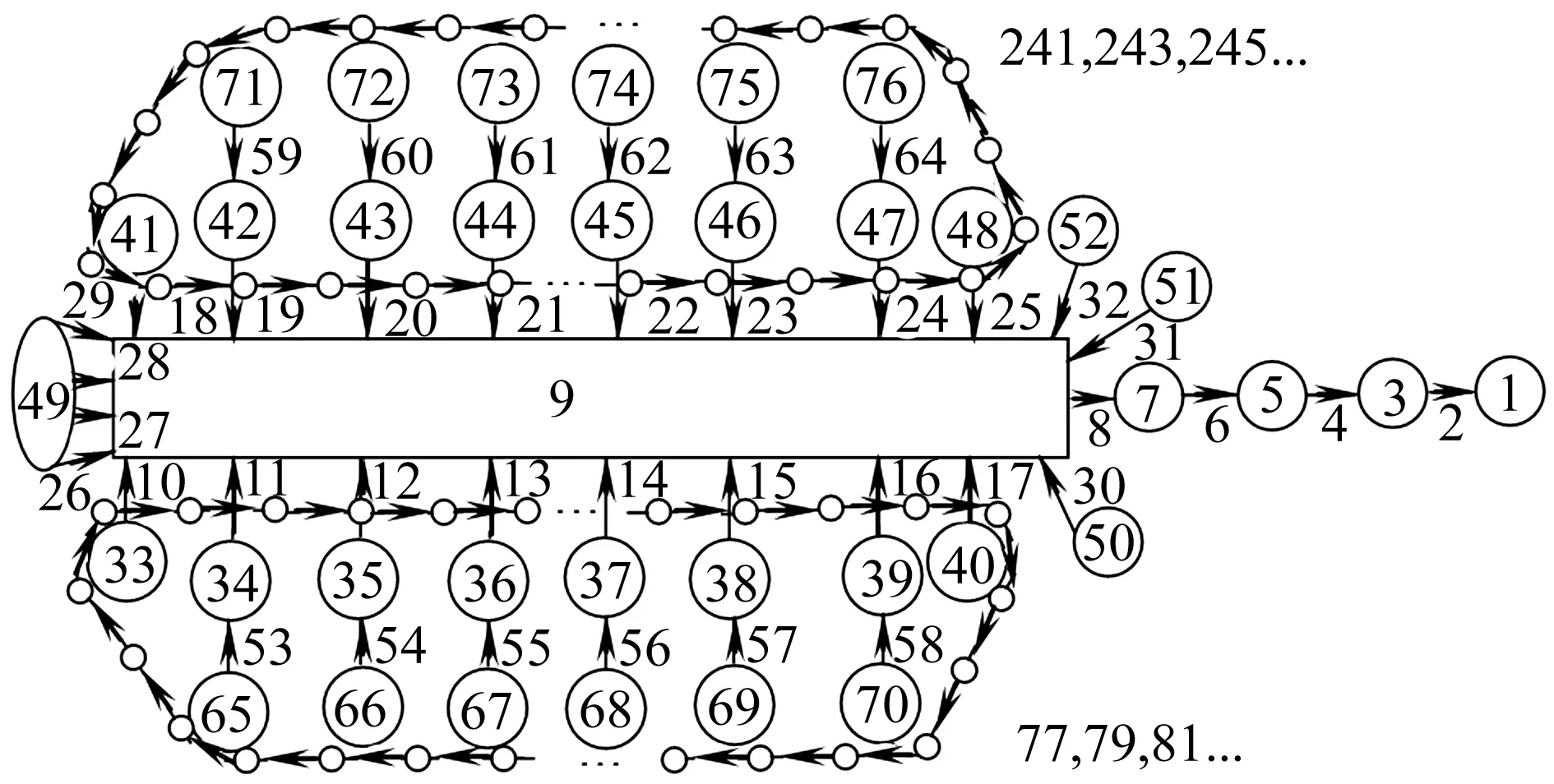
图2　坦克多体系统发射动力学模型拓扑图Fig.2 Topological graph of launch dynamics of the tank multi-body system

2坦克系统总传递方程及矩阵

2.1柔性身管动力学方程

通过质点系动量定理及质点系相对动量矩定理分别获得浮动框架平动方程及转动方程为

(1)

(2)

柔性梁横、纵向振动微分方程分别为

(3)

(4)

(5)

L=H1ξ,u=H1u+H2v+H3w

(6)

(7)

(8)

(9)

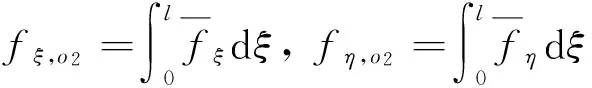
(10)

式中：Ao2为柔性梁浮动框架在全局惯性坐标系中方向余弦矩阵；ro2为o2点相对与惯性系原点绝对位置；ωo2柔性梁浮动框架绝对角速度在全局惯性坐标系的投影；E为身管弹性模量；Iy，Iz为身管截面积惯性矩；l为身管长度。

2.2身管动力学方程离散

考虑身管动力学方程作为含复杂数学函数的非线性方程组，直接进行数值求解十分困难，故用模态叠加法将身管弯曲变形表示为一些列模态函数与模态坐标的乘积，建立适合数值计算的离散形式。

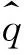
(11)

(12)

(13)

将式(11)～式(13)代入式(1)～式(5)，可得身管动力学方程的离散形式。

2.3坦克系统总传递方程及矩阵

结合柔性身管动力学方程，据坦克多体系统行驶与发射动力学模型及拓扑结构、多体系统总传递方程自动推导定理[17]，自动列写该系统总传递方程为

Uallzall=0

式中：Uall为系统总传递矩阵；zall为系统状态矢量。

连接点处线加速度、角加速度、内力矩及内力在全局惯性坐标系中描述。

3行进间射击弹丸膛内运动方程

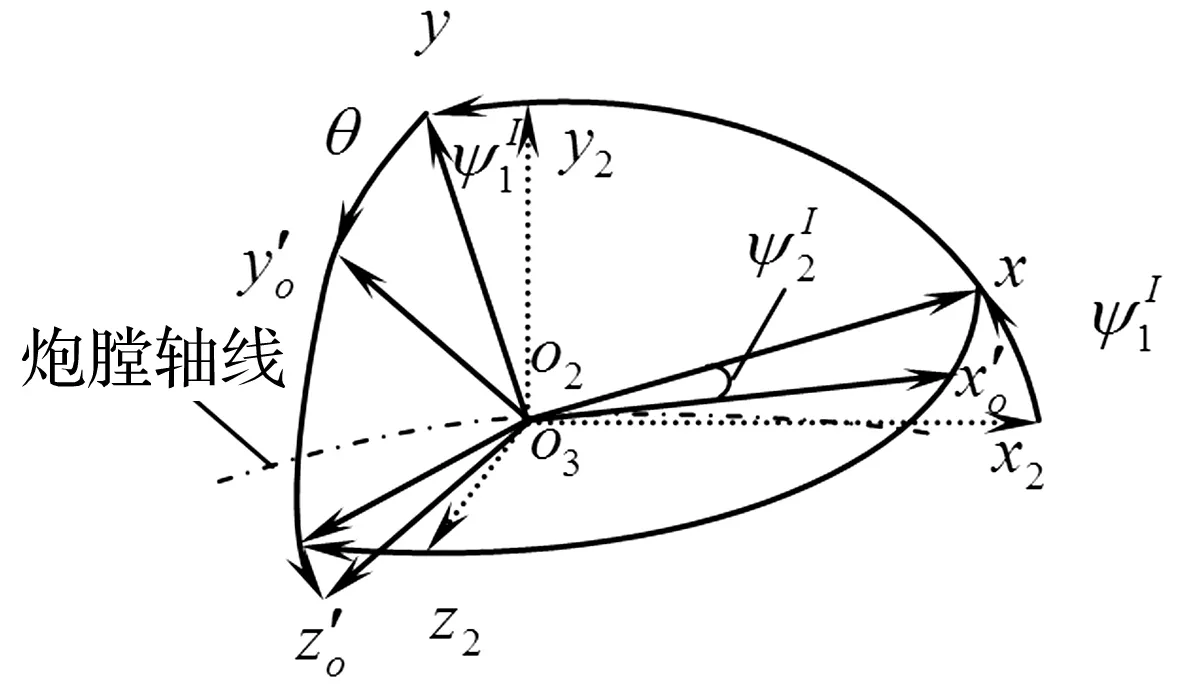
图3　火炮系与身管系Fig.3 The artillery coordinates system and the barrel coordinates system

3.1受力分析

弹丸与身管的相互作用极其复杂，引入身管连体坐标系后，仍将弹炮相互作用力在火炮系中表述，弹炮相互作用力矩在弹轴系中表述，故文献[1-3]中弹炮相互作用力、力矩仍适用。

弹丸所受重力矩阵形式为

(14)

式中：g为重力加速度。

重力对弹丸几何中心o1的力矩为

(15)

弹丸质心C所受合外力对弹丸几何中心o1的合力及合力矩为

(16)

(17)

式中：FP为火药气体压力；MP为FP对弹丸几何中心o1力矩；Fc为弹带与炮膛接触力；Mc为Fc对弹丸几何中心o1的力矩；Fs为定心部与炮膛接触力；Ms为Fs对弹丸几何中心o1的力矩。

身管受作用力、力矩除弹丸对身管作用力及力矩外，亦受火药气体对炮身的作用合力、波尔登力及后坐阻力等。火药气体压力计算采用混合装药的内弹道方程[17]，即

(18)

3.2行进间射击弹丸膛内运动方程

在火炮系中描述弹丸质心运动方程，在弹轴系中描述弹丸转动微分方程，以弹轴系o1ξηζ为动坐标系，弹丸几何中心o1为基点，用牛顿第二运动定律

F=maC

(19)

转动坐标系相对动量矩定理

(20)

可得行进间射击弹丸膛内运动方程为

(21)

式中：

ro1C=[0lmηlmζ]T;lmη=lm1cosγ-lm2sinγ

lmζ=lm1sinγ+lm2cosγ

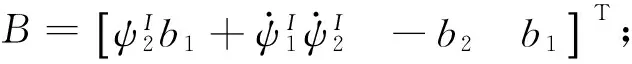
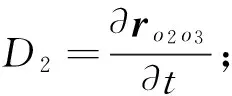
Ν=[0(A-C)βDζ-(A-C)βDη]T

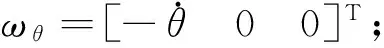
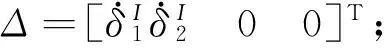
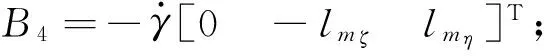
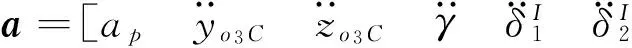
4数值求解分析

在进间弹丸膛内运动方程及柔性身管动力学方程基础上，以某坦克为计算原型，结合多体系统总传递方程自动推导定理编制坦克发射动力学仿真程序。某坦克基本参数为：火炮口径125 mm，弹丸有效行程5.28 m，炮管线密度及抗弯刚度见表1。坦克制动于水平路面以0°射角射击时，利用坦克发射动力学仿真程序所得弹丸速度仿真曲线见图4。

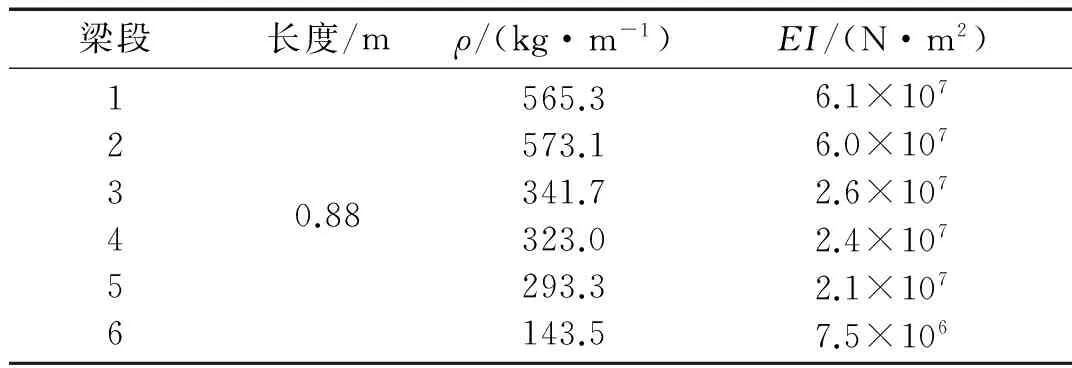
表1　炮管参数

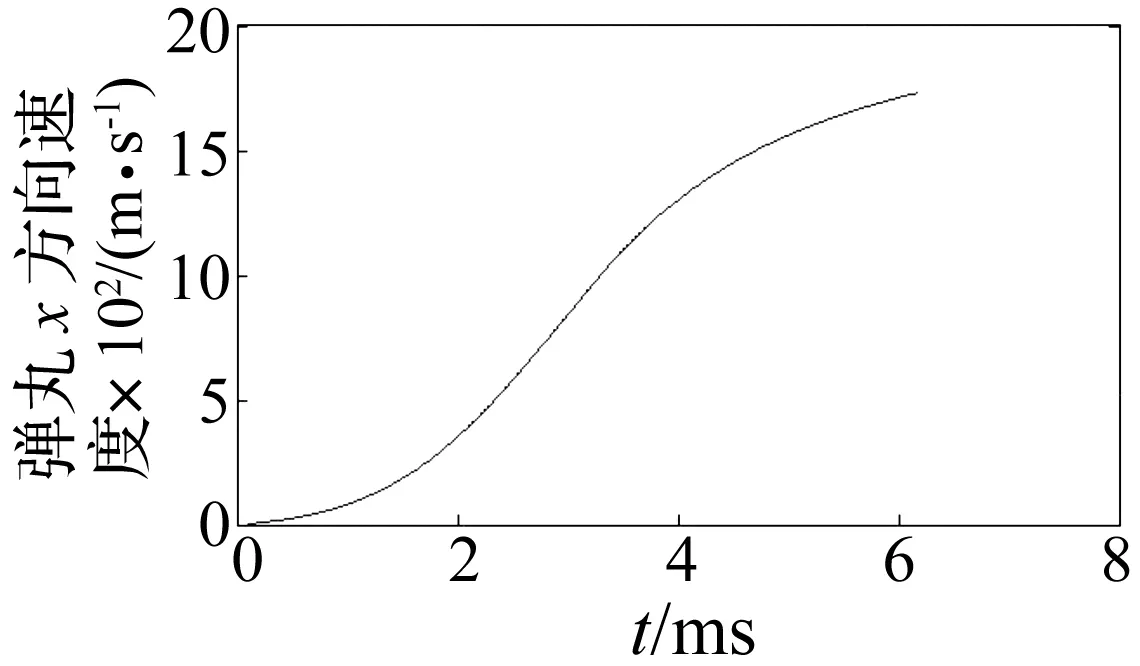
图4　弹丸速度仿真结果Fig.4 Computational results of the velocity of projectile

常温下坦克制动于水平路面并以0°射角射击时炮口初速仿真与试验结果见表2，可见仿真误差为-0.8%。

表2　炮口初速仿真与试验结果对比

坦克制动于水平路面上并以0°射角射击时，利用坦克发射动力学仿真程序所得弹底压力仿真结果见图5，最大膛压仿真与试验结果见表3，仿真误差为-0.2%。

图5 弹底压力仿真曲线Fig.5Computationalresultsofprojectilebasepressure图6 弹炮碰撞力仿真结果Fig.6Computationalresultsoftheimpactforcebetweenthebarrelandthebourrelet图7 弹丸铅垂摆动角速度仿真结果Fig.7Computationalresultsoftheverticalswingangularvelocityofprojectile

表3　最大膛压仿真与试验结果对比

利用坦克发射动力学仿真程序，对坦克以20 km/h车速在D级路面上行使并以0°射角射击进行仿真，所得弹炮碰撞力仿真结果见图6，弹丸铅垂摆动角速度见图7。由图6看出，考虑身管柔性效应后与刚性身管相比，弹丸前定心部与身管碰撞变化较大：相同仿真条件下碰撞力幅值相差明显，碰撞次数也不同。结合图6、图7看出，弹丸与身管第一次碰撞前，柔性身、刚性身管中弹丸铅垂摆动角速度一致性较好；弹丸与身管碰撞后随弹丸不断运动，身管的柔性效应对弹丸铅垂摆动角速度影响显著。

柔性身管受重力作用产生的静挠度仿真结果见图8，仿真条件为坦克制动于水平路面，炮管射角和方向角均为0°射角。柔性、刚性身管炮口在竖直、侧向的位移仿真结果(仿真条件为坦克行驶速度20 km/h，路面等级D，弹丸射击时刻1 s，射角、方向角均为0°) 见图9、图10。可见图9中柔性、刚性身管炮口侧向位移变化趋势一致，说明身管刚性运动起主要作用；弹丸发射后柔性身管较刚性侧向振动更明显。图10中柔性、刚性身管炮口垂向位移变化趋势一致，说明身管刚性运动起主要作用，柔性身管铅垂振动相对线位移最大量为0.312 m，较刚性身管相对线位移最大量0.304 m增加0.008 m，与实际趋势一致。因此，考虑身管的柔性特性，能有效提高坦克射击过程的动态仿真精度。

图8 身管的静挠度仿真结果Fig.8Computationalresultsofthestaticdeflectionofthebarrel图9 炮口侧向位移仿真结果Fig.9Computationalresultsofthelateraldisplacementofbarrelmuzzle图10 炮口铅垂位移仿真结果Fig.10Computationalresultsoftheverticaldisplacementofbarrelmuzzle

坦克以20 km/h车速在D级路面上行使并以0°射角射击时计算所得弹丸起始扰动见表4(符号同前)。

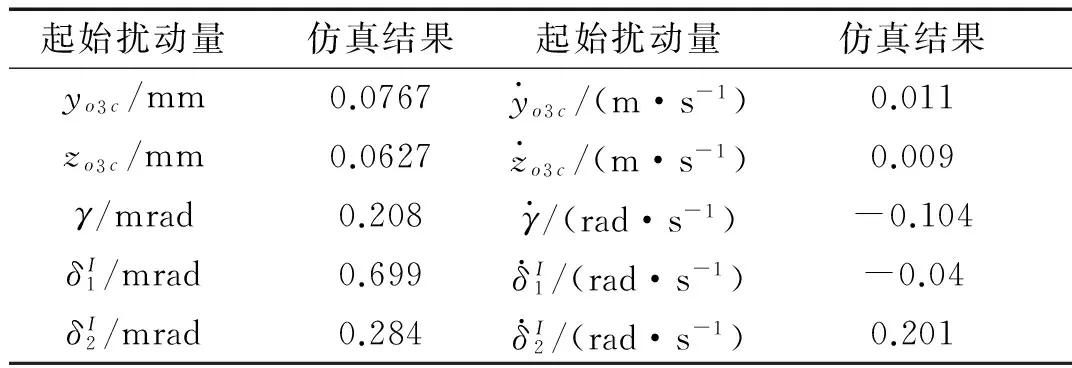
表4　弹丸起始扰动仿真结果

千米立靶密集度仿真与试验数据见表5。其中，停车射击仿真条件为坦克制动于水平路面，射角、方向角均为0°，射击弹丸200发；行进射击仿真条件为坦克行驶速度20 km/h，路面等级D，弹丸射击时刻1 s，仿真时间2 s，射角、方向角均为0°，射击弹丸200发；刚性身管仿真条件为不考虑身管柔性，坦克制动于水平路面，射角、方向角均为0°，射击弹丸200发；仿真方法为以弹炮间隙、质量偏心距、动不平衡角、弹丸质量、弹丸转动惯量、装填角偏移量及装填线偏移量为随机量，利用蒙特卡洛法仿真；试验条件为坦克制动与水平路面，射角、方向角均为0°；停车射击仿真误差为1.6%(高低)、3.7%(方向)，即仿真行进间射击密集度较停车射击密集度差，与实际趋势一致；刚性身管仿真误差为14.6%(高低)、18.3%(方向)，即仿真的刚性身管射击密集度较试验射击密集度及柔性身管停车射击仿真所得射击密集度好，亦与实际趋势一致。利用刚性身管模型的仿真、试验结果误差较柔性身管模型的仿真、试验结果误差大 (13%以上)，表明本文建立的柔性身管动力学模型及编制的坦克行进间发射动力学仿真程序正确可行。

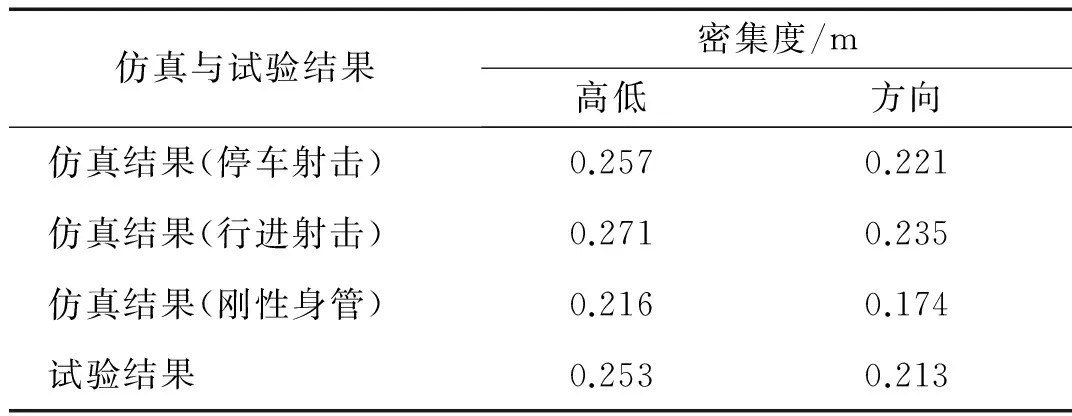
表5　千米立靶密集度仿真与试验结果

5结论

(1) 建立计及身管柔性的坦克发射动力学模型及行进间弹丸膛内运动方程，仿真获得弹丸、身管在膛内运动的响应、起始扰动及千米立靶密集度等，并部分仿真结果得到试验验证。

(2) 通过分析计及身管柔性后坦克炮口振动的动力学变化，明确身管柔性对炮口垂向位移及弹丸发射过程中弹炮碰撞力影响显著，说明须考虑身管柔性对系统影响，才能较准确获得弹丸起始扰动。

(3) 身管柔性对坦克射击密集度影响显著，不考虑身管柔性仿真结果较试验结果误差大于14%；考虑身管柔性仿真结果与试验结果吻合较好(误差在5%以内)，说明必须考虑该影响，才能较真实反映系统动态特性，提高坦克系统行进间射击精度。

参 考 文 献

[1] 芮筱亭,刘怡欣,于海龙.坦克自行火炮发射动力学[M].北京:科学出版社,2011.

[2] 贠来峰. 自行火炮发射动力学研究[D]. 南京:南京理工大学,2002.

[3] 芮筱亭,杨启仁. 弹丸发射过程理论[M]. 南京:东南大学出版社,1992.

[4] 管红根,袁人枢,高树滋,等. 车载炮发射动力学仿真研究[J]. 兵工学报, 2005, 26(1): 53-55.GUAN Hong-gen, YUAN Ren-shu, GAO Shu-zi, et al. Simulation and analysis of launching dynamics of automobile carried howitzer [J]. ActaArmamentarii, 2005, 26(1): 53-55.

[5] 邓辉咏,马吉胜,刘海平.履带式自行火炮发射动力学建模与仿真研究[J]. 机械科学与技术, 2012, 31(4): 543-546.

DENG Hui-yong, MA Ji-sheng, LIU Hai-ping. Research on model building and simulation of self-propelled gun firing dynamics[J]. Mechanical Science and Technology for Aerospace Engineering, 2012, 31(4): 543-546.

[ 6] 芮筱亭,陆毓琪,陆文广,等.自行炮发射动力学研究[J]. 兵工学报, 2000, 21(增刊):38-40.

RUI Xiao-ting, LU Yu-qi, LU Wen-guang, et al. A study on the launch dynamics of self-propelled artillery[J]. Acta Armamentarii, 2000, 21(Sup): 38-40.

[7] 芮筱亭,贠来峰,陆毓琪,等.多管火箭发射动力学研究[J]. 兵工学报, 2004, 25(5): 556-561.

RUI Xiao-ting, YUN Lai-feng, LU Yu-qi, et al. A study on the launch dynamics of multiple launch rocket system [J]. ActaArmamentarii, 2004, 25(5): 556-561.

[8] 冯长根,温波,李才葆. 自行火炮行进间射击动力学研究[J]. 兵工学报, 2002, 23(4): 457-461.

FENG Chang-gen, WEN Bo,LI Cai-bao. Dynamic analysis of a self-propelled gun firing on the move[J]. Acta Armamentarii, 2002, 23(4): 457-461.

[9] 闵建平,谭俊杰,李剑峰. 行进间射击时的动力学研究[J]. 振动与冲击, 2003, 22(4): 88-90.

MIN Jian-ping, TAN Jun-jie,LI Jian-feng. Study on dynamics of self-propelled guns at firing on the move [J]. Journal of Vibration and Shock, 2003, 22(4): 88-90.

[10] 李剑峰,王剑,李振平,等. 履带车辆行进间射击的随机响应研究[J]. 车辆与动力技术,2009,3:9-12.

LI Jian-feng, WANG Jian,LI Zhen-ping,et al. Research on random response for tracked vehicle marching fire[J]. Vehicle and Power Technology, 2009, 3: 9-12.

[11] 王颖泽,张小兵,袁亚雄. 计及柔性效应的火炮身管动力学模型分析[J]. 火炮发射与控制学报, 2008, 4:49-58.

WANG Ying-ze, ZHANG Xiao-bing, YUAN Ya-xiong. Flexible dynamics model analysis of gun tube [J]. Journal of Gun Launch and Control, 2008, 4:49-58.

[12] 徐达,胡俊彪,穆歌. 基于刚柔耦合的坦克炮发射动力学仿真分析[J]. 装甲兵工程学院学报, 2009, 23(4): 45-47.

XU Da, HU Jun-biao, MU Ge. Simulation analysis on tank gun firing dynamics based on rigid-flexible coupling [J]. Journal ofAcadeny of Armored Force Engineering, 2009,23(4): 45-47.

[13] 马吉胜,王瑞林. 弹炮耦合问题的理论模型[J]. 兵工学报, 2004, 25(1): 73-77.

MA Ji-sheng, WANG Rui-lin. A theoretical model for the projectile-barrel coupling problem [J]. ActaArmamentarii, 2004, 25(1): 73-77.

[14] 谢润，杨国来.自行高炮行进间射击炮口响应特性研究[J].兵工学报,2014, 35(8):1158-1163.

XIE Run, YANG Guo-lai. Research on response characteristics of muzzle for self-propelled antiaircraft gun firing on the move[J]. Acta armamentarii,2014,35(8): 1158-1163.

[15] Shabana A A. Dynamics of multi-body system[M].4th ed.USA: Cambridge University Press, 2013.

[16] 芮筱亭,贠来峰,陆毓琪,等. 多体系统传递矩阵法及其应用[M]. 北京: 科学出版社,2008.

[17] Rui Xiao-ting, Zhang Jian-shu, Zhou Qin-bo. Automatic deduction theorem of overall transfer equation of multibody system[J].Advances in Mechanical Engineering, 2014，6：378047.

[18] 金志明. 枪炮内弹道学[M]. 北京:北京理工大学出版社, 2004.

基金项目：装备预研共用技术基金(9140A10041013BQ02143)

收稿日期：2015-01-16修改稿收到日期：2015-06-20

通信作者芮筱亭 男，博士，教授，博士生导师，1956年8月生

中图分类号:TJ38；TJ811

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.02.010

Influence of barrels’ flexibility on the launch dynamics of tank during marching fire

LIU Fei-fei, RUI Xiao-ting, YU Hai-long, ZHANG Jian-shu, GU Jun-jie

(Institute of Launch Dynamics，Nanjing University of Science & Technology, Nanjing 210094, China)

Abstract:The high first round hit probability during marching of the tank is extremly important in modern war. The flexibility of the barrel has great influence on the launch process, and the initial disturbance on the projectile is the premier factor which takes effect on the marching fire accuracy. A dynamic model of the tank ( with flexible barrel) was established. Considering the mass eccentricity and the dynamic unbalance of the projectile, the projectile-barrel interaction and the gap between projectile and barrel, the launch dynamics equations during marching were derived. A simulation program of launch dynamics for the tank during marching was compiled. The motion law of projectile in bore and the 1 000 m vertical target dispersion were simulated, and the results of simulation were verified by tests. The study provides both the theoretical foundation and the simulation approach for improving the marching fire accuracy of tank systems.

Key words:flexible barrel of the tank; marching fire; launch dynamics; fire accuracy; movement of the projectile in bore

第一作者 刘飞飞 男，博士生，1986年2月生