“三线摆”测物体定轴转动惯量的实验原理

石大立，刘春晖，吴艳阳

（武汉工程大学机电工程学院力学教研室，湖北 武汉430073）



“三线摆”测物体定轴转动惯量的实验原理

石大立，刘春晖，吴艳阳

（武汉工程大学机电工程学院力学教研室，湖北 武汉430073）

摘要:“三线摆”实验中，摆动周期由测量摆盘系统的转动惯量决定。只要摆盘上放置物体，测量摆盘系统转动惯量就会改变，则其摆动周期随之改变。因此，实验求取：两个圆柱及待测物对中心轴转动惯量和时，必须分别做两个摆盘空载时、两个摆盘加载被测物后的扭振实验各两次；再根据实验结果，间接获得被测物转动惯量；并且由实验数据表的项数据，可判断实验结果的准确性；最后再运用插入法求得零件转动惯量。特别运用两组不同的学生实验数据来验证该实验的原理。对实验的误差分析，说明提高扭振周期的测量精度，可显著提高实验结果的准确性。“三线摆”实质是振动系统，属于单自由度无阻尼自由振动问题，因此本文着重从理论方面讨论了单自由度系统的自由振动。

关键词:转动惯量；三线摆；扭振周期；固有频率；阻尼

转动惯量是刚体转动时的惯性量度，其量值取决于物体的形状、质量分布及转轴的位置。外形复杂、质量分布不均匀的物体，只能通过实验的方法来精确地测定物体的转动惯量[1]。实验测定转动惯量的方法有：利用转动定律原理制成的转动惯量仪，利用机械能守恒定律制成的三线摆或悬丝扭摆等方法[2]。本实验用三线摆测定物体的转动惯量。

1　“三线摆”法测取不规则物体的定轴转动惯量

浙江大学TME—1理论力学多功能实验装置如图1所示。两个具有相同线长和相同直径的“三线摆”，其上各放置不同的物体，物体质量相同。当两个“三线摆”摆动具有相同的周期，则两个物体的转动惯量相等[3]。三线摆扭转周期T与盘的转动惯量JO有关，如式（1）[2，3]。

图1　实验装置

运用公式（1）实验时，其有关的实验原理、步骤很有必要加以规范和说明。本文所涉及的转动惯量，单位和数量级均为（kg·m2）×10-6.

1.1实验原理及步骤[1，3-4，6-7]

实验中，在求取两个圆柱对中心轴转动惯量的实测值JM及待测物对中心轴转动惯量的实测值JM2时，都必须做相应扭振实验，共计四次扭振实验，涉及四类扭振周期，然后间接获得被测物转动惯量。实验步骤如下：

（1）薄圆盘与尺空载，做扭振实验，并用秒表测量相应的扭振周期T0（s），之后由公式（2）求得薄圆盘与尺空载时的转动惯量实测值JM0.

（2）薄圆盘与尺加载两个圆柱后，再次做扭振实验，并用秒表测量相应的扭振周期T1（s），再由公式（3）求得圆盘与尺加载两个圆柱后的转动惯量实验值JM+M0.

（3）由公式（4）间接获得两个圆柱对中心轴的转动惯量实测值JM.

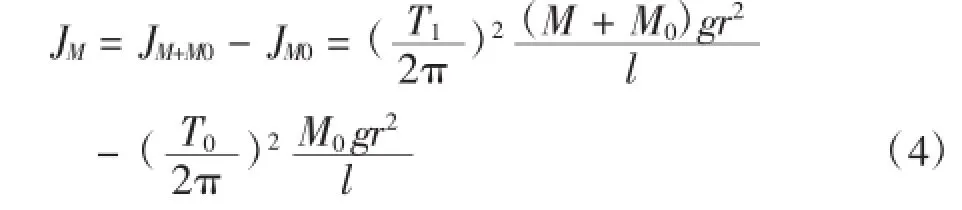
（4）薄圆盘空载，做扭振实验，并用秒表测量相应的扭振周期T2（0s），然后由公式（5）求得薄圆盘空载时的转动惯量实测值JM20.

（5）薄圆盘加载待测物后，再次做扭振实验，并用秒表测量相应的扭振周期T2（s），由公式（6）得薄圆盘加载待测物后的转动惯量实测值JM2+M20.

（6）由公式（7），间接获得待测物的转动惯量。

1.2实验数据验证[6]

学生在实验过程中很困惑、经常犯错误，同一套实验装置竟做出了两个差距很大的结果，且没有判断正误的标准。而当实验原理、步骤，加上了实验数据后，就有足够的说服力。运用两组不同的学生实验数据来验证该实验的原理。按照1.1的实验步骤，分别做了两次试验，获得表2和表3的两组实验数据。表1是实验基本数据。

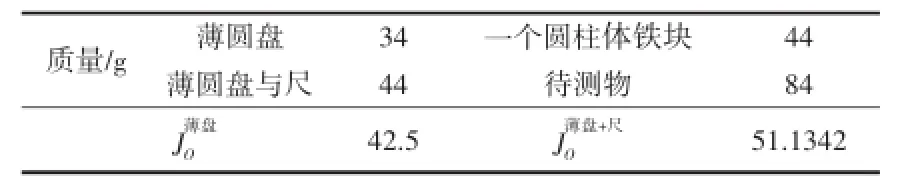
表1　实验改进后必须事先已知的重要物理量数据表

表2是实验改进后，“三线摆”测物体定轴转动惯量的学生实验数据（一），它不符合要求。因为：η2≥12.88%；=69.7746，JM2=57.0129×10-（6kg·m）2，η3=18.29%.

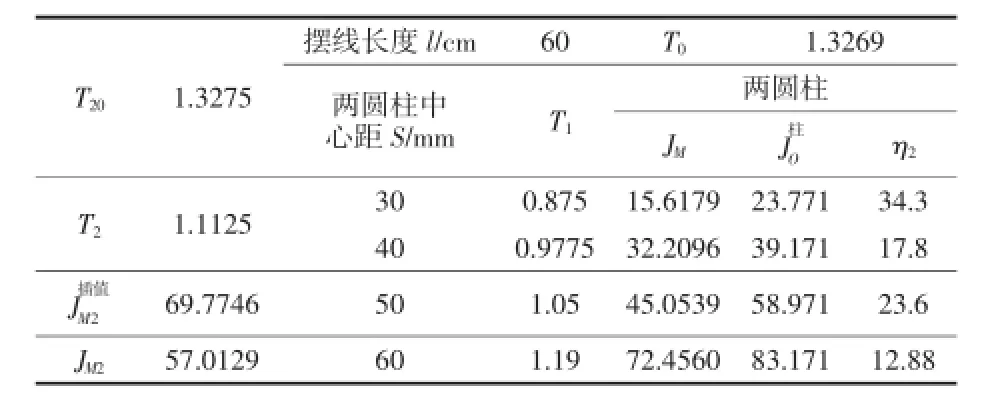
表2　“三线摆”测物体定轴转动惯量的学生实验数据（一）

表3是实验改进后，“三线摆”测物体定轴转动惯量的学生实验数据（二），它符合要求。因为：η2≥13.364%=55.0308，JM2=54.2783×10-（6kg·m）2，η3=1.367%.

表3　“三线摆”测物体定轴转动惯量的学生实验数据（二）

注意到：表2和表3的数据中，由η2项数据可判断实验数据的准确性；且JM2比更准确。表2和表3中，两个圆柱对中心轴转动惯量=2[mr2+m （）2].

1.3实验误差分析[2]

本实验由四个扭振周期T0，T1，T20，T2获得转动惯量JM0，JM+M0，JM20，JM2+M20.根据误差理论，这些转动惯量属于间接测量结果，其合成不确定度为[2]

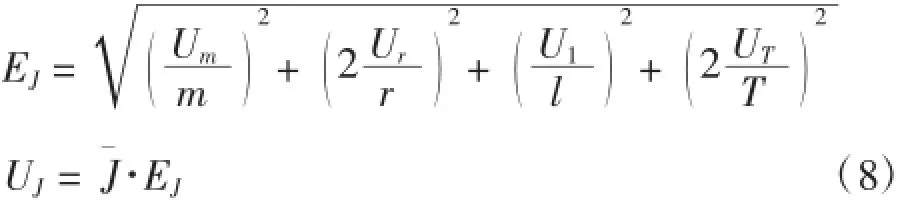
尤其，当实验中扭振周期T1测量不准确时，实验结果的准确性会受到很大影响。

因为J∝T2，所以周期T的精度对J的影响较大，且T是手动机械秒表测量，其仪器误差△t=0.2 s.对T的相对不确定度作估算，考虑T=1.40 s，0.9 s，0.8 s（不考虑随机误差）[2]，则T的测量不确定度传递到间接测量量J的相对不确定度如式（9），分别为16.496%，25.66%，28.868%.

而其他量，如摆线长等，其相对不确定度较小。因此，测量中应尽量提高周期T的测量精度。实验时测量悬盘扭转几十个周期nT所用的时间t0，t0=nT，这样每个周期的仪器误差就只有原来的，再测量三次以减小随机误差[2]。

2　三线摆测取物体定轴转动惯量的实验原理[2，6，8]

三线摆可以测定任意形状物体相对于某轴的转动惯量。悬盘（圆盘）绕垂直于盘面并通过盘面中心的轴线作扭转运动，其重心可以沿转动轴移动。摆动周期由盘的转动惯量决定。如果悬盘上放上任一物体，则摆动周期就要变为另一值[1]。详见“1.1实验原理及步骤”。

如将汽车发动机摇臂的转轴中心放在悬盘中心实验，可得悬盘和汽车发动机摇臂共同体对中心轴的转动惯量，如式（6）。还必须对空载薄圆盘做扭振实验，由公式（5）得薄圆盘空载转动惯量实测值JM20。再按照转动惯量的相加性，汽车发动机摇臂转动惯量如式（7）[2，3，6]。

三线摆实质是振动系统，可建立振动运动微分方程（10）。

2.1扭转振动[8]

用角位移θ作为广义坐标来表达其振动状态的扭转振动。对扭转振动建立其运动微分方程式。此时，牛顿定律的表达式为：

式中，M为施加于转动物体上的力矩；I为转动物体对于转动轴的转动惯量；θ咬为角加速度。扭转振动运动微分方程式（11）与直线自由振动微分方程（13）完全相似，其通解为：

扭转振动属于单自由度系统自由振动问题，因此很有必要分析其运动规律。

3　单自由度系统自由振动[8，9]

单自由度系统有阻尼自由振动的运动微分方程式

这是一个二阶常系数线性齐次微分方程。设其解为x=est，可求得特征方程：

ωn为系统振动的圆频率。α称为衰减系数。定义阻尼比ζ，ζ＝.见图2.初始条件：t＝0时，x=x0，=

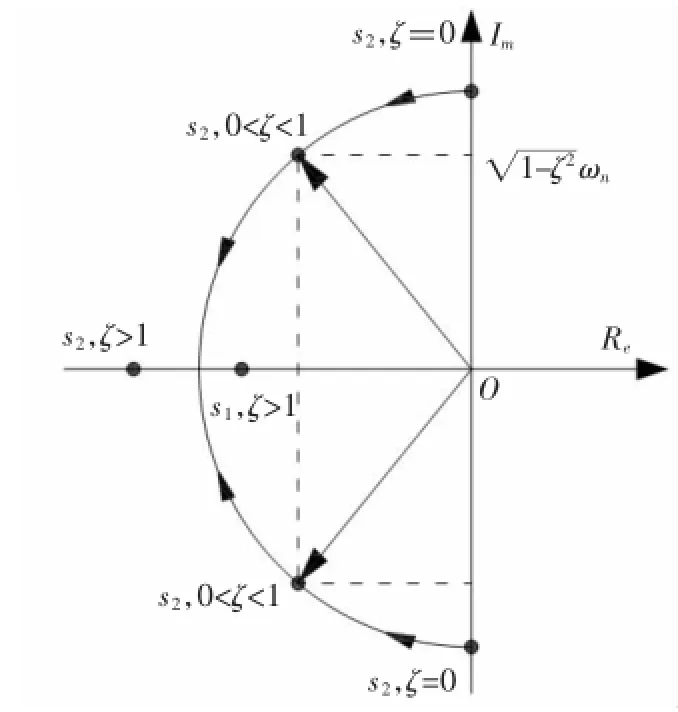
图2　特征根分布

（1）无阻尼，ζ＝0，（14）式的特征根为纯虚数：s1，2=±iωn，单自由度无阻尼自由振动的运动方程式为：x（t）=Asin（ωnt+φ），x（t）为等幅振动，如图3（a）所示。式中

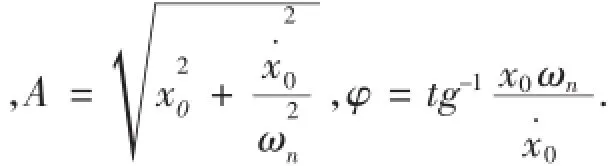
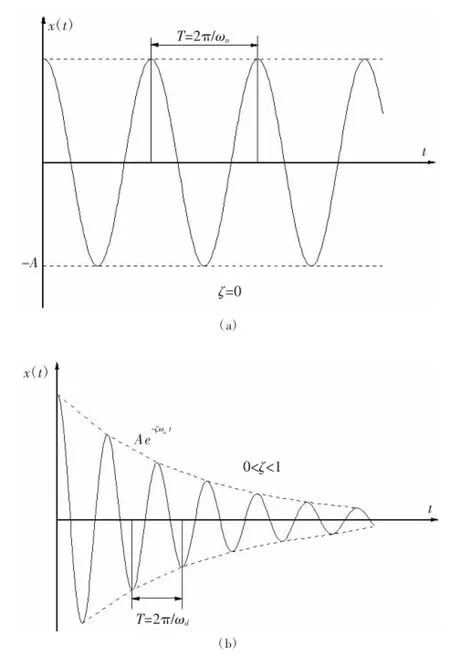
图3　有阻尼振动运动规律

（4）临界阻尼（ζ=1）时，（14）式的特征根为两重实根-ωn，微分方程式（13）的解为：

式（16），（17）中，A1、A2均是待定常数。临界阻尼和过阻尼状态下，系统的运动都是一个逐渐回到平衡位置的非周期运动。特征根的虚部，决定自由振动的频率。而临界阻尼和过阻尼，其特征根均为实数，无虚部，故系统的运动都不是振动。

4　结束语

（1）求取被测物对中心轴的转动惯量实测值时，必须做相应的扭振实验，再间接获得被测物的转动惯量。不同的实验数据会得到不同的转动惯量，由实验数据表的η2项，可以判断实验数据准确性。在已经判断了实验数据确实准确以后，再运用插入法求得零件转动惯量才有实际意义。扭振周期T1测量不准确时，对实验结果的准确性影响极大。

（2）三线摆实质是振动系统，可建立振动运动微分方程式，并且是单自由度无阻尼自由振动问题。特征根的虚部，决定了自由振动的频率。无阻尼时特征根存在虚部，x（t）为振动。

参考文献：

[1]成正维.大学物理实验[M].北京：高等教育出版社，2002，92-102.

[2]冯忠耀.大学物理实验[M].北京：机械工业出版社，2009，108-115.

[3]庄表中，王惠明.应用理论力学实验[M].北京：高等教育出版社，2009，56，60-69，86-88.

[4]张勇.三线摆刚体转动惯量测量实验数据处理的新方法[J].内江科技，2011，32（8）:95-95.

[5]张代胜.三线摆法测定复杂构件转动惯量的误差分析[J].农业机械学报，2008，39（3）：32-34.

[6]石大立.“三线摆”测定不规则物体定轴转动惯量的实验研究[J].装备制造技术，2016，（3）:21-24.

[7]吴晓.三线摆法测定转动惯量的计算原理分析[J].振动与冲击，2011，30（9）:154-156.

[8]顾海明，周勇军.机械振动理论与应用[M].南京：东南大学出版社，2007:1-57.

[9]同济大学.高等数学[M].第四版.北京：高等教育出版社1998:366-386.

中图分类号:O313.3

文献标识码：A

文章编号：1672-545X（2016）04-0013-05

收稿日期：2016-01-04

作者简介：石大立（1962-），男，山东省诸城人，学士，工程师，研究方向：数学力学。

The Experimental Principle of Measuring the Moment of Inertia of the Fixed Axis of the Three Wire Pendulum

SHI Da-li，LIU Chun-hui，WU Yan-yang
（Department of Mechanics，School of Mechanical and Electrical Engineering，Wuhan Institute of Technology，Wuhan Hubei 430073，China）

Abstract:In the experiment of three wire pendulum，the swing period is determined by the moment of inertia of the measuring pendulum system.The moment of inertia of the measuring pendulum system will be changed whenever an object is placed on its wobble-plate，so its swing period will be changed then.Therefore，when you do experiments to obtain the moment of inertia of the two cylinders rotating about the central axis and the moment of inertia of the object to be tested rotating about the central axis，two kinds of the torsional vibration experiments must have been done separately four times when each wobble-plate is unloaded and after each wobble-plate is loaded the object.According to the results of these experiments，the moment of inertia of the object to be tested is obtained indirectly.The accuracy of experimental results can be judged by the data itemof the experimental data table.Then the moment of inertia of the part is finally obtained by applying the method of inserting.In particular，the principle of the experiment is verified by using the experiment data of two different groups of students.Error analysis of the experiment shows that improving the measurement accuracy of the swing period can significantly improve the accuracy of the experimental results.In essence，three wire pendulum is a vibration system，belonging to the problem of free vibration of a single freedom degree and undamped system，hence this paper discusses the free vibration of a single degree of freedom system emphatically from the aspects of theory.

Key words:moment of inertia；three wire pendulum；swing period；natural frequency；damping