基于Robotics Toolbox的6R型机械臂运动学仿真及分析

史召峰，陈周五

(安徽工业经济职业技术学院　机械与汽车工程学院，安徽　合肥　230051)



基于Robotics Toolbox的6R型机械臂运动学仿真及分析

史召峰，陈周五

(安徽工业经济职业技术学院机械与汽车工程学院，安徽合肥230051)

摘要：针对6R型机械臂运动学进行了研究。首先采用D-H法建立机械臂关节坐标系并确定其连杆参数，应用MATLAB软件中的Robotics Toolbox仿真工具箱建立该机械臂模型，其次对机械臂进行轨迹规划研究和运动学仿真，最后，基于机械臂运动学模型应用可操作度指标分析机械臂的灵巧性能，本文阐述了机械臂运动学仿真的一般规律，由仿真得出的结果可知，本文的研究对于关节型机械臂的运动学仿真具有重要意义。

关键词：Robotics Toolbox；轨迹规划；运动学仿真；灵活性

机械臂运动学是机器人研究领域的基础课题，包括位姿层面的运动学研究和速度层面的运动学研究。关于机械臂的运动学研究，国内外不少学者对其进行了探索和研究，其中研究较多的是PUMA系列机器人和斯坦福机器人，干敏耀等基于MATLAB软件平台对PUMA机械臂进行了研究，分析其运动学特性并对其进行仿真[1]；张微微等针对Stanford机器人进行研究，分析了其动力学性能并对其运动学进行仿真[2]；卢锐等针对PUMA560机器人作了分析，并基于机器人工具箱对其运动学进行了仿真[3]；李宪华等对一种机械臂进行运动学研究并构建了其3D仿真平台[4]；孙亮等针对一六自由度机械臂对其进行轨迹规划和仿真研究，并开发出其仿真平台[5]；谢乃柳等基于六自由度机械臂提出一种算法，对机械臂轨迹规划进行了研究和分析并验证算法的正确性[6]；赵京等提出用主成分分析法分析机械臂运动灵活性，并以空间3R机械臂为例进行验证[7]。

上述研究中多以PUMA和Stanford机器人为例，本文则以一种6R型川崎机械臂为研究对象，首先采用D-H法对机械臂进行运动学建模，得到各连杆的DH参数，并用机器人工具箱建立机械臂模型，其次，分别在机械臂关节空间和笛卡尔空间对其运动轨迹进行规划，分析其运动特性，最后，基于可操作度椭球指标分析机械臂的灵活性。机械臂的运动学分析及仿真不仅可以直观的反映末端执行器在基础坐标系中位姿随各关节变量的变化情况，而且能反映出机械臂的关节速度与末端操作速度之间的关系，同时得到运动过程中各关节位置、速度及加速度随时间的变化关系，在仿真过程中，可以观测到机械臂的运动情况，而且结果以图形的形式直观地显示出来。

1机械臂D-H模型建立

本文研究的机械臂由6个转动关节组成，根据机械臂的结构构型如图1所示,采用D-H法建立机械臂的各关节处连杆坐标系, 完整的关节坐标系模型如图2所示，建立好坐标系模型后，根据各个连杆之间的关系就可以确定该机械臂的D-H参数，如表1所示。其中θi为第i关节角度值，ai为相邻关节间的杆件长度，di为相邻关节间的杆件偏移量，αi为相邻坐标系间的扭转角，其中α、a、d为固定值，θ为变量。

图1　机械臂本体结构

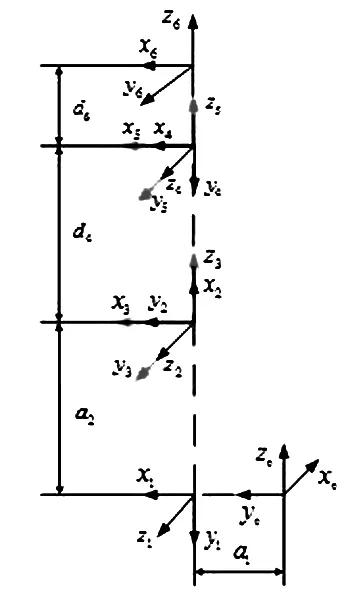
图2　机械臂关节坐标系

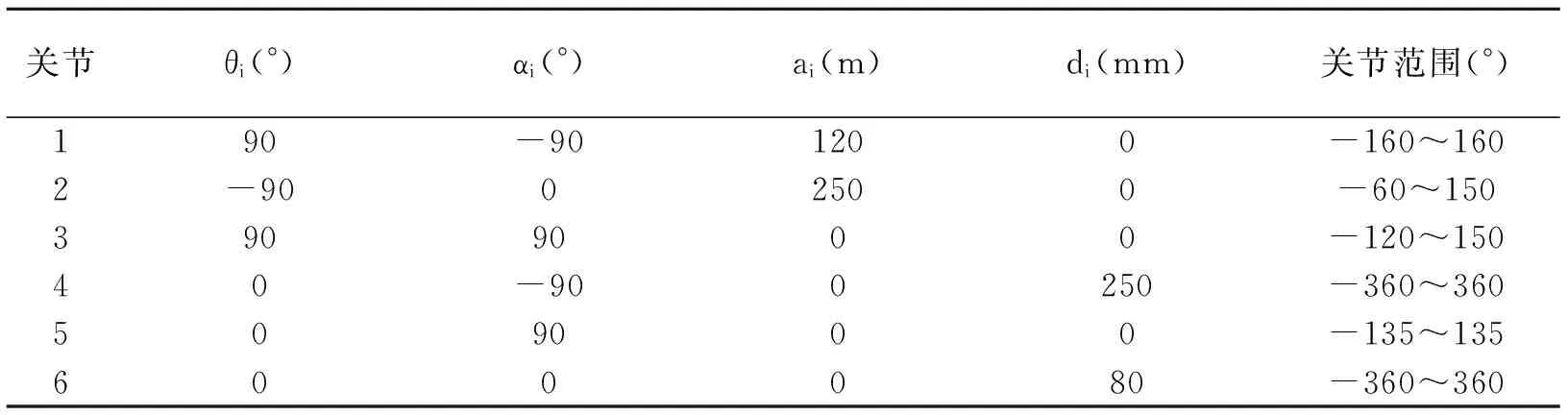
关节θi(°)αi(°)ai(m)di(mm)关节范围(°)190-901200-160～1602-9002500-60～1503909000-120～15040-900250-360～360509000-135～135600080-360～360

其中：Cθi表示cos(θi)，Sθi表示sin(θi)。

(1)

2机械臂模型建立

Robotics Toolbox工具箱里面设有机械臂研究所用到的的运动学、动力学和轨迹规划等方面的函数，应用该工具箱除了可以进行数值计算，还能够对机械臂进行图形仿真，方便观测其运动规律和过程。在MATLAB软件环境下，应用Robotics Toolbox工具箱中的Link函数和Serial Link函数来建立机械臂的模型，Link函数的一般通式为L=Link([Theta D A Alpha Sigma], CONVENTION),其中Theta表示关节变量角，D表示偏距，A表示连杆长度，Alpha表示扭转角，Sigma代表关节类型：0为转动关节，1为移动关节，CONVENTION可以取‘standard’和‘modified’,即‘standard’为采用标准的D-H参数，而‘modified’代为采用改进的D-H参数，根据表1中的机械臂DH参数，构建机械臂模型的命令如下：

L(1)=Link([Pi/2 0 120 -Pi/2 0]，‘standard’)；%构建机械臂第一关节

L(2)=Link([-Pi/2 0 250 0 0]， ‘standard’)；%构建机械臂第二关节

L(3)=Link([Pi/2 0 0 Pi/2 0]， ‘standard’)；%构建机械臂第三关节

L(4)=Link([0 250 0 -Pi/2 0]， ‘standard’)；%构建机械臂第四关节

L(5)=Link([0 0 0 Pi/2 0]， ‘standard’)；%构建机械臂第五关节

L(6)=Link([0 80 0 0 0]， ‘standard’)；%构建机械臂第六关节

Rob = SerialLink(L,’Name’,’Rob’)； %构建机械臂，并命名为Rob

Teach(Rob)； %示教机械臂的6个关节变量，观测机械臂的实时位姿。

执行程序命令后即可得到机械臂的滑块控制图和初始姿态如图3和图4所示，可以看出机械臂处于初始位姿时的情况，通过调节图3中的滚动条可以直观的观测到机械臂的各个关节变化时，机械臂的位姿变化情况。

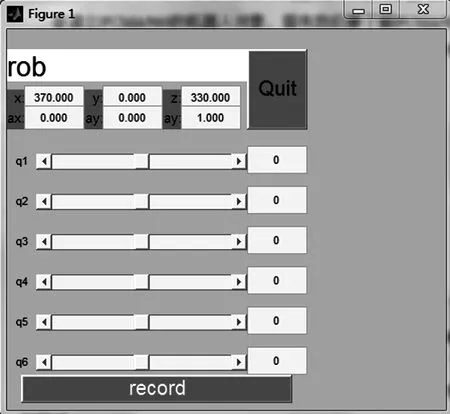
图3　滑块控制图图

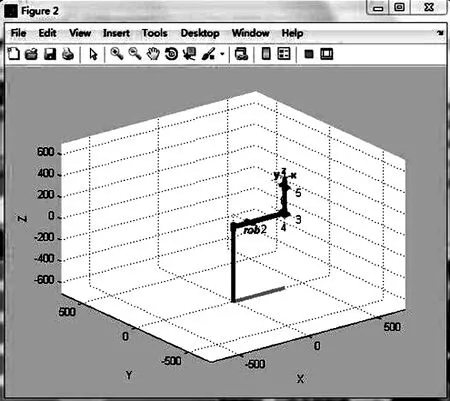
图4　初始姿态

3运动学正解仿真

机械臂的运动学正解仿真可以直接有效的验证其绝对定位精度和重复定位精度，在各个关节都能够到达的范围内，随机给每个关节变量取三个数值，分别为：[Pi/4 Pi/4 Pi/4 0 -Pi/4 0]、[Pi/2 -Pi/2 -2×Pi/3 0 -Pi/2 Pi/2]、[4×Pi/5 -Pi/2 Pi/3 Pi 0 -Pi/2]，在图3所示的控制面板中输入以上随机选的三组关节角度，机械臂在基础坐标系中的位姿和会由程序自动计算出来，经过验证，所得的三组机械臂的位姿和式(1)计算得到的位姿一致,验证了在MATLAB中建立的机械臂的模型的正确性。

4机械臂轨迹规划

对于机械臂轨迹规划研究，通常的轨迹规划方式有两种：一是机械臂关节空间的规划，二是机械臂笛卡尔空间的规划，此两类轨迹规划方式优缺点并存：机械臂关节空间的轨迹规划相对简单，算法相对容易且计算量小，但会导致在其在笛卡尔空间的运动轨迹不易观测；机械臂笛卡尔空间的轨迹规划比则较容易观察且直观，但在运动过程中机械臂易出现奇异形位，从而导致关节速度和加速度非常大，不利于控制。因此有必要对两种规划方式分别研究，这里对该机械臂分别作两种规划仿真，在MATLAB软件环境下，在计算机械臂的正逆解时应用Robotics Toolbox工具箱中的Fkine函数和Ikine函数，计算关节空间和笛卡尔空间的运动轨迹时利用Jtraj函数和Ctraj函数。

4.1机械臂关节空间轨迹规划

设定机械臂仿真时间为5s，本文采用TPT运动，即机械臂初始的关节值是q0=[0 0 0 0 0 0]，终止的关节值是q1=[ Pi/3 -Pi/2 Pi/4 Pi/8 0 Pi/2]，在MATLAB中执行q=Jtraj(q0,q1,t)程序命令则可得到采用5次多项式插值方法的各个关节的变化曲线和各个关节速度和加速度的变化曲线，如图5所示。

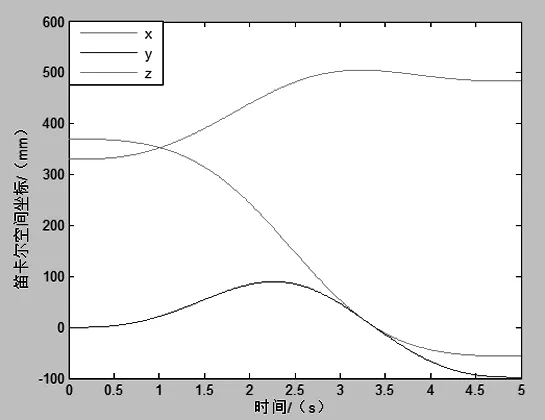
(a)　末端位置

(c)　关节加速度

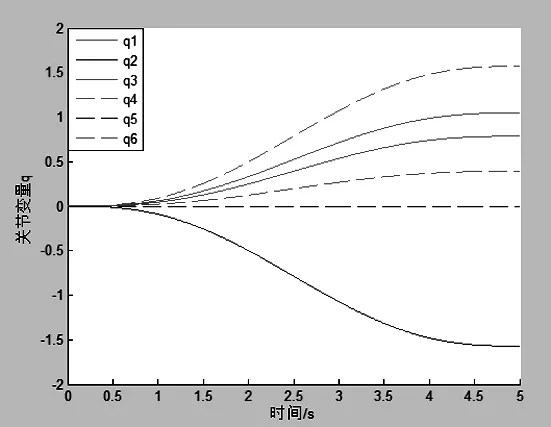
(b)　关节变量

(d)　关节速度

由前文分析可知，给定各个关节变量的值，就可以求得该机械臂末端在基础坐标系中的变换矩阵T，由该矩阵T，计算出末端执行器在基础坐标系下的位置和姿态。由图5(b)中规划好的的各组关节角，利用Robotics Toolbox工具箱中Fkine函数求得相应的齐次变换矩阵T，用命令Plot(t，Transl(T))就可以得到机械臂末端执行器在笛卡尔空间中的位置变化曲线，如图5的(a)所示。为了能够直观的观察末端的运动范围，分别做出末端运动轨迹在三个坐标平面中的投影曲线，如图6所示。

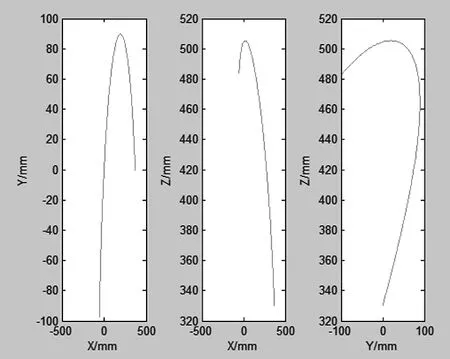
图6　末端轨迹在三坐标面投影

4.2机械臂笛卡尔空间规划

我们实际控制机械臂时，只是要求机械臂能够示教到要求轨迹上的一些比较重要的点，再根据机械臂的运动方式特征求解得到这些重要的点之间的位置点，最后通过在这些点之间采用插补的方式进行轨迹规划控制，进而达到高精度的机械臂运动控制。本文取空间两点A和空间B两点为例，进行笛卡尔直线轨迹规划，其中A和B位姿的齐次变换矩阵为：

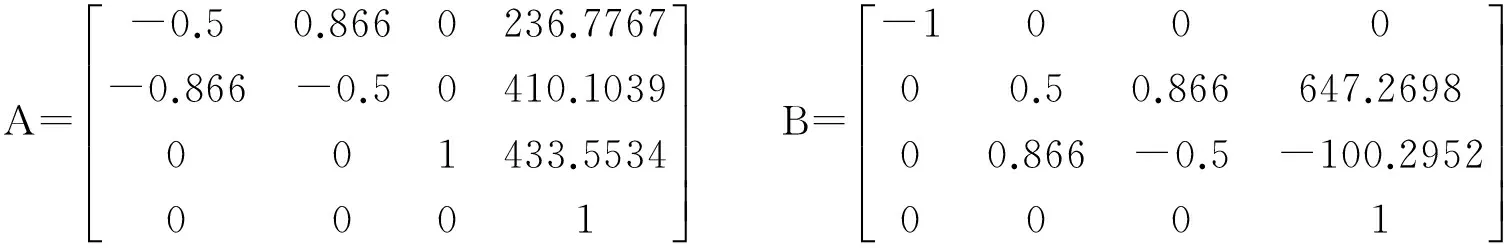
利用Ctraj函数进行从A到B的笛卡尔间轨迹规划，时间为5s，可以得到此过程中末端执行器的轨迹曲线，结果如图7所示，进一步可以得到上述规划过程中机械臂末端的路径点图,如图8所示。

图7　末端轨迹曲线

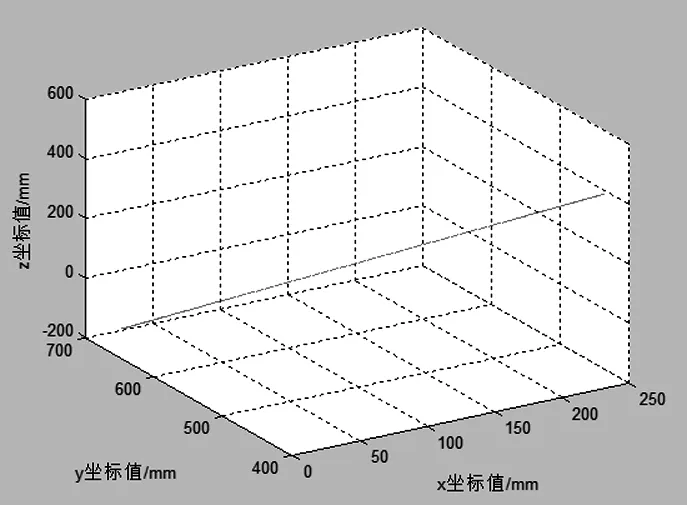
图8　末端路径点图

在MATLAB环境下对机械臂进行关节空间和笛卡尔空间轨迹规划,直观的看出各个关节的位置、速度和加速度随时间的变化情况，以及末端执行器的运动轨迹，为后续的机械臂避障规划研究奠定了基础。

5机械臂灵巧性分析及仿真

机械臂灵巧性的指标有很多，本文采用Yoshikawa提出的可操作度指标和可操作度椭球来分析机械臂的灵巧性能[8]。Yoshikawa定义可操作度为

(2)

式中：

σi—雅克比矩阵的奇异值，i=1,2,…m；

机械臂沿各个方向上运动能力的大小就是可操作度的物理意义，可以看作是机器人的整体灵活性的综合指标。在此基础之上，Yoshikawa定义了可操作度椭球，如图9所示，椭球各轴的方向与(J(q)JT(q))-1的特征向量一致，各轴长等于其特征值平方根的倒数，也等于J的奇异值。

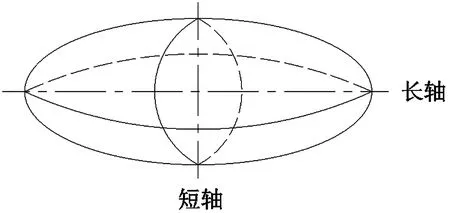
图9　可操作度椭球

在MATLAB软件环境下，应用工具箱中的Jacob0函数来计算该机械臂的雅克比矩阵，并在MATLAB中作出末端的可操作度椭球，分析其灵巧性能。由于篇幅原因，本文仅对该机械臂的工作空间内的一个确定位姿进行灵巧性能分析，即关节角为[Pi/3 -Pi/3 2×Pi/3 Pi/8 Pi/2 Pi/2]时，其余原理相同，此时机械臂的位姿如图10所示，所求得的机械臂在此位姿时的末端移动速度椭球和末端转动速度椭球如图11所示。

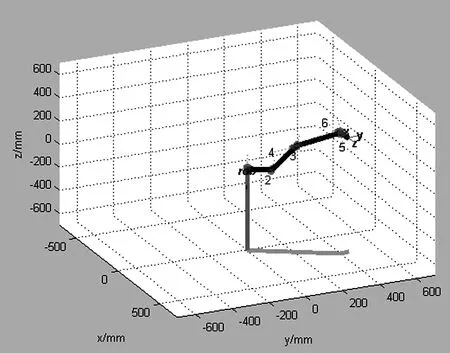
图10　机械臂位姿

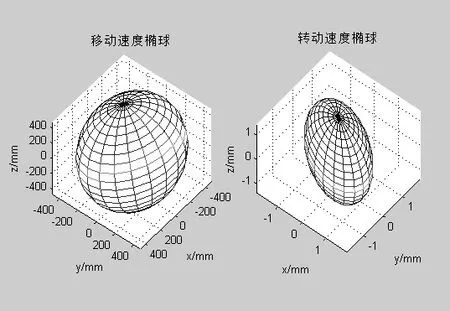
图11　速度椭球

经过仿真可以看出，机械臂此时刻位姿时，如图10所示，其末端的移动速度椭球和末端的转动速度椭球分别如图11中所示，由图中可以看出椭球的都比较接近球，说明个机械臂在此位姿时的灵活性能比较好，其中半径小的方向说明机械臂沿此方向的运动能力有所下降，反之，在半径比较大的方向上，机械臂的运动能力较好，即灵活性能较好。当机械臂在关节奇异形位时，机械臂的可操作度椭球在某个方向上面接近为一个平面，说明沿该方向机械臂几乎不能够运动。机械臂的灵巧性仿真为后续的机械臂避障规划研究提供了依据。

6结论

本文针对6R型川崎机械臂，借助MATLAB软件中Robotics Toolbox工具箱，基于机械臂D-H参数建立该6R型机械臂的模型，完成对机械臂的关节空间和笛卡尔空间的轨迹规划的仿真，得到各关节的变化曲线，验证该变化是否满足各个关节位置、速度和加速度的要求，并应用机械臂的可操作度指标，利用机械臂雅克比矩阵绘制机械臂的可操作度椭球，研究和分析了机械臂在工作空间中确定位姿时的灵巧性，为以后的机械臂的避障规划研究奠定了基础，具有非常高的现实意义。

参考文献：

[1]干敏耀,马骏骑,陈永星,等. 基于MATLAB的PUMA机器人运动学仿真[J]. 昆明理工大学学报:理工版,2003(6):50-53.

[2]张微微,郭希娟. Stanford机器人动力学性能分析与仿真[J]. 计算机仿真,2007(5):138-141.

[3]卢锐，王忠庆.基于MATLAB Robotics TOOIs的机械臂仿真[J].电子世界,2014,(18):417-418.

[4]李宪华,张雷刚,张军,等. 一种机械臂运动学研究及3D仿真平台构建[J].安徽理工大学学报：自然科学版,2014,(3):39-44.

[5]孙亮,马江,阮晓钢. 六自由度机械臂轨迹规划与仿真研究[J].控制工程, 2010, 17(3):388-392.

[6]谢乃流,陈劲杰,石岩. 基于六自由度机械臂的轨迹规划[J].机械制造与自动化, 2011,40(1):141-144.

[7]赵京,李立明,尚红,等. 基于主成分分析法的机械臂运动灵活性性能综合评价[J]. 机械工程学报, 2014,50(13):9-15.

[8]Yoshikawa T. Manipulability of robotic mechanism [J].Int Jof Robotics Research, 1985,4(2):3-9．

(责任编辑：李孟良)

收稿日期：2016-01-05

基金项目：安徽省省级教学研究项目(2014jyxm559)；安徽省省级教学团队(2015tszy067)。

作者简介：史召峰(1978-)，男，安徽省合肥市人，硕士，讲师，主要从事机电控制及CAD/CAM/CAE技术研究。

中图分类号：TP241

文献标识码：A

文章编号：1673-8772(2016)02-0060-07

Kinematic Simulation and Analysis of 6R Manipulator Based on Robotics Toolbox

SHI Zhao-feng,CHEN Zhou-wu

(School of Mechanical & Automotive Engineering, Anhui Technical College of Industry and Economy, Hefei 230051,China)

Abstract：The kinematics of manipulator was studied aimed at 6R manipulator. Firstly, the joint coordinate system of manipulator was established using D-H method and the parameters of its links were determined, then the manipulator model was established by using Robotics Toolbox simulation Toolbox of MATLAB. Secondly, the trajectory planning and kinematics simulation of manipulator were studied. Lastly, the flexibility of the manipulator was analyzed by using manipulability index based on the kinematic model of manipulator. This article describes the general laws of manipulator kinematic simulation, the results show that this study has important signi

-ficance for simulation of an articulated manipulator.

Key words:Robotics Toolbox; Trajectory planning; Kinematics simulation; Flexibility