直接空冷机组最佳背压计算方法及应用
2016-07-23翟永杰刘金龙
翟永杰, 米 路, 刘金龙
(华北电力大学 自动化系, 河北保定 071003)
直接空冷机组最佳背压计算方法及应用
翟永杰,米路,刘金龙
(华北电力大学 自动化系, 河北保定 071003)
摘要:分析了直接空冷机组运行中背压的主要影响因素,基于机组运行数据,采用支持向量机和粒子群算法建立了一个最佳背压计算模型,分析了背压与发电机功率和空冷风机耗功功率的关系.以某300 MW直接空冷机组为研究对象,利用所建模型计算得出不同负荷段内不同环境温度所对应的最佳背压;在DCS里设计背压优化调节方案,将最佳背压送入背压调节逻辑中参与控制.结果表明:直接空冷机组最佳背压随负荷和环境温度的升高而升高;最佳背压实际应用后,能够在保证机组安全平稳运行的前提下提高经济效益.
关键词:直接空冷机组; 最佳背压; 发电机功率; 空冷风机耗功; 支持向量机
20世纪80年代末我国开始引进空冷技术,与传统的水冷技术相比,直接空冷技术可以实现全厂节水60%以上,且直接空冷机组还具有占地面积少、运行灵活方便等优势,因而直接空冷技术在我国北方缺水地区得到了越来越广泛的应用.然而,空气的换热能力远低于水,相比水冷机组,直接空冷机组的背压偏高,使得其热耗率偏高,且背压波动较大,易受负荷和外界环境的影响.此外,直接空冷机组的空冷风机耗电量大,使得机组的厂用电率偏高[1].
降低机组背压会增大汽轮机出力,进而提高发电量,但背压的降低是以提高空冷风机转速为代价的,即背压降低的同时会增大空冷风机耗电量[2].目前,直接空冷机组背压的设定以运行人员经验为主,如何在保证机组安全平稳运行的前提下,找到机组背压的最佳值,使得机组在此背压下运行的经济效益最显著是目前迫切需要解决的问题.
目前,针对直接空冷机组最佳背压的研究尚处于初级阶段,相关文献较少,且以机理研究为主.高建强等[2]基于直接空冷机组的过程机理,建立了最佳背压的计算模型.赵洪滨等[3]从理论上研究了排汽量、环境温度等因素对最佳背压的影响规律.郭民臣等[4]借鉴湿冷机组最佳背压的研究方法,采用变工况特性,计算了不同环境温度和排汽热负荷下机组的最佳背压.然而,机理研究需要依据汽轮机和空冷岛侧详细的结构参数和运行特性,而这些参数往往很难获得,且不同机组的运行特性差异较大.因此,笔者基于机组实际运行数据,以某300 MW直接空冷机组为研究对象,采用支持向量机和粒子群算法建立了直接空冷机组的最佳背压计算模型,并对原DCS背压控制逻辑进行优化,使最佳背压能实际参与控制.
1直接空冷系统热力模型及背压影响因素分析
直接空冷凝汽器为表面式换热器,通过管外空气的强制对流进行换热.直接空冷系统顺流区结构如图1所示,机组正常运行时,在汽轮机内做功后的蒸汽经由汽轮机排汽管道进入空冷凝汽器,饱和蒸汽先从上往下流过顺流区凝汽器管束,冷空气被风机自下往上吹入管束外侧的散热器,饱和蒸汽与冷空气进行热量交换,部分饱和蒸汽凝结为水,直接流入管束下部的凝结水联箱[5].
凝汽器管束内蒸汽凝结放热量方程[6]为
(1)
式中:Qn为单位时间蒸汽凝结放热量,kJ;qm,n为汽轮机排汽质量流量,kJ/h;hn为汽轮机排汽焓,kJ/kg;hsn为凝汽器凝结水焓,kJ/kg.
管外空气吸热量方程为
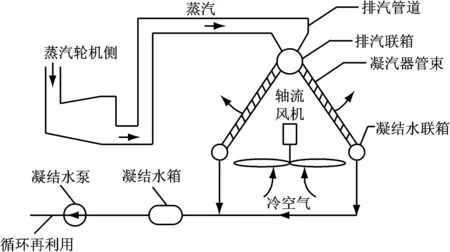
图1 直接空冷系统顺流区结构图
(2)
式中:qm,a为冷却空气质量流量,kJ/h;cp为空气的比定压热容,kJ/(kg·K);ta1为凝汽器入口空气温度(环境温度),℃;ta2为凝汽器出口空气温度,℃;Δta为空气的温升,K;SF为凝汽器迎风面积,m2;vf为迎面风速,m/s;ρa为空气密度,kg/m3.
由式(1)和式(2)可得出能量平衡方程:
(3)
在直接空冷机组实际运行过程中,影响背压的因素有负荷、环境温度、空冷风机运行方式、环境风向、散热器清洁度和真空系统严密性等.笔者仅从主要因素入手,分析负荷、环境温度和空冷风机运行方式对机组背压的影响.
1.1背压与发电机功率的关系
发电机与汽轮机同轴连接,由汽轮机带动发电,发电机功率P与汽轮机输出功率Pq的关系[7]为
(4)
式中:ηq、ηf分别为汽轮机机械效率和发电机效率,二者均与背压pc无关,则背压对发电机功率的影响转化为背压对汽轮机输出功率的影响.
当汽轮机进汽量及运行参数不变时,直接空冷机组背压变化对汽轮机输出功率的影响主要考虑2点:(1) 排汽焓变化引起的汽轮机末级做功量变化W1;(2) 凝结水温度改变使末级抽汽量变化,引起的做功损失变化W2.则:
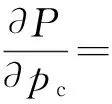
(5)
式中:ηi为级的相对内效率;qm,fw为凝结水质量流量,kJ/h;cp,w为凝结水比定压热容,kJ/(kg·K);Y为末级抽汽效率.
1.2背压与空冷风机耗功功率的关系
空冷风机的耗功功率可由下式[8]计算:
(6)
式中:η1为风机效率,一般不小于65%;η2为传动效率,直联时η2=100%;ηd为电机效率;p为风机出口总压,Pa;Cs为海拔高度校正系数,可由手册查得.
风机出口总压为当地环境的静压与风机出口动压之和,即
(7)
其中,
式中:ps为当地环境的静压,Pa;pd为风机出口动压,Pa;D为风机叶轮直径,m.
对于已投运的直接空冷机组,由于其结构参数已定,故空冷风机的耗功功率仅与冷却空气质量流量qm,a和凝汽器入口空气温度ta1有关,则有:
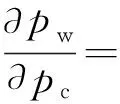
(8)
由式(1)和式(2)可得:
(9)
则有:
(10)
式(5)和式(8)分别为发电机功率-背压、空冷风机耗功功率-背压的函数关系式,在第3节中根据机组运行数据对发电机功率-背压、空冷风机耗功功率-背压关系曲线进行拟合时,需不断优化拟合算法中的参数,使拟合曲线与式(5)、式(8)的函数关系相一致.
1.3环境温度对背压的影响
直接空冷系统是以环境空气作为冷却介质对汽轮机排汽进行冷却的,空气的冷却能力和传热系数较低决定了背压对环境温度特别敏感.因此,环境温度也是影响背压的一个重要因素.
当汽轮机排汽质量流量、冷却空气质量流量等其他影响背压的因素不变时,环境温度升高,凝汽器入口空气温度升高,冷却空气的温差变小,凝汽器冷凝效果变差,背压升高[9].在第2第和第3节中,根据机组运行数据分析发电机功率-背压、空冷风机耗功功率-背压的关系及求取最佳背压时,需将环境温度值限定在很小的变化范围内,以消除环境温度对背压的影响.
2最佳背压计算方法
2.1理论依据
直接空冷机组的供电功率E主要与发电机功率P、空冷风机耗功功率pw和电厂其他设备耗电U有关[2],即
E=P-pw-U
(11)
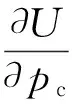
(12)
将式(12)改写为差分方程形式,背压变化所产生的供电功率增量为
(13)
按照直接空冷机组最佳背压的一般定义,凝汽器背压变化后机组发电机功率增量与空冷风机耗电功率增量之差最大时的背压为最佳背压.因此,机组在某负荷段,在一定的背压运行参数范围内,改变pc值,显然增量函数大于0的区间为背压变化增益区,增量函数小于0的区间为背压变化非增益区.如果能找到一点pc=pcbs,使得增量函数最大,即
(14)
则称pcbs为直接空冷机组的最佳背压.
2.2数据处理及计算流程
为了确定最佳背压,首先需确定发电机功率和空冷风机耗功功率随背压的变化关系.以某300 MW直接空冷机组为例,从厂级监控信息系统(SIS)中提取负荷、环境温度、背压、空冷岛供电电压、空冷岛供电电流和主蒸汽质量流量等运行数据,由空冷岛供电电压、空冷岛供电电流求得空冷风机耗功功率.该机组正常运行时负荷一般在180 MW以上,笔者从负荷为180 MW开始,每隔20 MW计算一段不同环境温度下的最佳背压.数据处理及计算流程如图2所示.
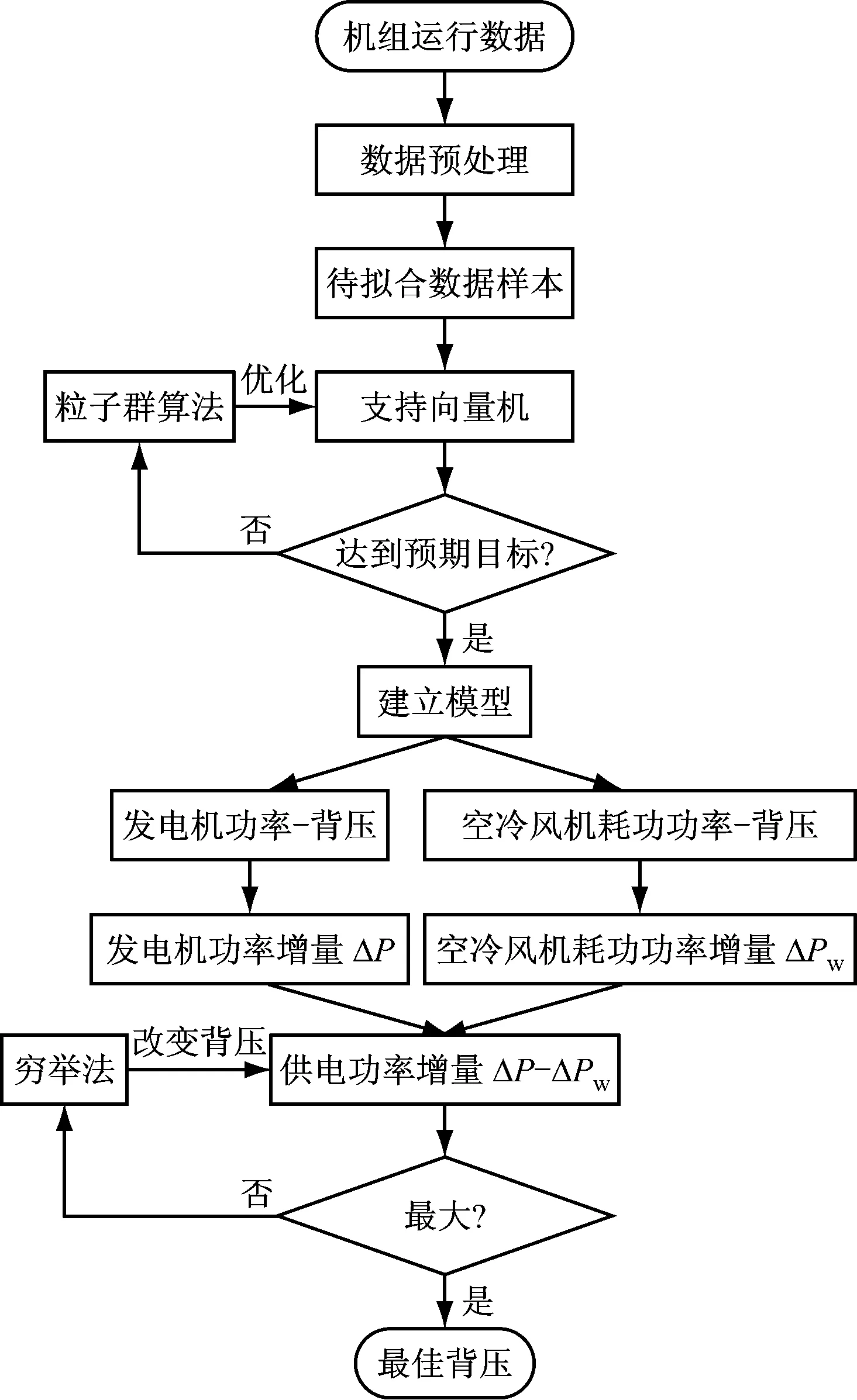
图2 最佳背压计算流程图
具体计算步骤如下:
(1) 将数据依负荷分为6段,即180~<200 MW、200~<220 MW、220~<240 MW、240~<260 MW、260~<280 MW以及280~300 MW.
(2) 在每一负荷段内,按照环境温度间隔1 K对数据进一步分类,如环境温度在5.5~<6.5 ℃范围内的数据归为环境温度为6 ℃的数据.
(3) 在每一负荷段内每个环境温度下,为了保证背压主要受负荷、空冷风机运行方式的影响,限定主蒸汽质量流量在其平均值的±1‰范围内变化[10],最后得到各个负荷段内不同环境温度下的负荷、背压和空冷风机耗功功率3组数据.
(4) 采用支持向量机分别建立每一负荷段内,每个环境温度下的发电机功率-背压、空冷风机耗功功率-背压关系模型.
(5) 采用粒子群算法对模型中的参数进行优化,分别得到发电机功率和空冷风机耗功功率随背压变化的曲线.
(6) 找出曲线中背压的最大值,并计算得出背压最大时的发电机功率和空冷风机耗功功率,以该工况点为基准点,采用穷举法,以0.1 kPa为步长,将背压逐渐降低至曲线中的背压最小值,并根据曲线分别计算各背压下的发电机功率和空冷风机耗功功率,以求得各背压下发电机功率和空冷风机耗功功率相对于基准点的增量,再对两者求差值得到各背压下的供电功率增量,当供电功率增量最大时,对应的背压值即为该负荷段内该环境温度下的最佳背压值.
2.3支持向量机与粒子群算法
构建回归型支持向量机模型进行数据拟合,拟合对象为发电机功率-背压和空冷风机耗功功率-背压.支持向量机模型中损失函数类型为ε-不敏感损失函数,核函数为RBF核函数,需要人为选取的参数包括惩罚因子C、精度ε、核函数宽度σ以及交叉检验参数v[11].
文献[11]~文献[12]指出,惩罚因子C过小容易导致欠学习现象,过大可能会导致过学习现象;精度ε较小时,模型预测准确度较高,但是支持向量的数目较多,ε较大时,模型预测准确度显著下降;当核函数宽度σ较大时会出现欠学习现象,σ较小时会出现过学习现象.因此,合理地选取参数对提高模型性能起着至关重要的作用.
目前,参数的选取方法主要包括经验选择法、实验试凑法、梯度下降法、网格法、交叉检验法、遗传算法以及粒子群算法等[12].基于算法的快速性和有效性,笔者采用交叉检验和粒子群算法相结合的算法,交叉检验能防止过拟合,在防止过拟合的前提下,采用粒子群算法找到最优的惩罚因子C、精度ε和核函数宽度σ,从而使支持向量机模型能够准确地辨识出发电机功率-背压、空冷风机耗功功率-背压的关系.
3计算结果与分析
以某300 MW直接空冷机组为例,当负荷段为240~<260 MW,环境温度为27 ℃时,对发电机功率-背压、空冷风机耗功功率-背压关系曲线进行拟合,结果如图3所示.其中,粒子群算法中粒子数为50,进化代数为80,遗忘因子为0.6,学习因子为[0.6 0.6];交叉检验法中的参数v为10;惩罚因子C、精度ε、核函数宽度σ的初始范围分别为[0,1 000]、[0.000 1,0.1]和[0.01,1 000].
从图3可以看出,发电机功率先随着背压的降低而增大,在背压为8.0 kPa时达到峰值,随后逐渐减小.图3中背压变化范围为5.0~15.5 kPa,当背压为15.5 kPa时,发电机功率为246.09 MW,空冷风机耗功功率为220.05 kW,以此工况点为基准点,在此背压变化范围内寻优,得到供电功率增量与背压的关系曲线(见图4).
从图4可以看出,该工况下,背压为9.5 kPa时的供电功率增量最大,则负荷段为240~<260 MW,环境温度为27 ℃时,最佳背压值为9.5 kPa.
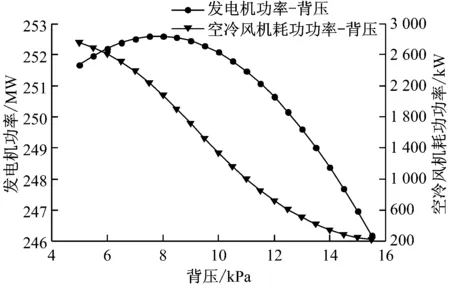
图3 发电机功率-背压、空冷风机耗功功率-背压的关系曲线
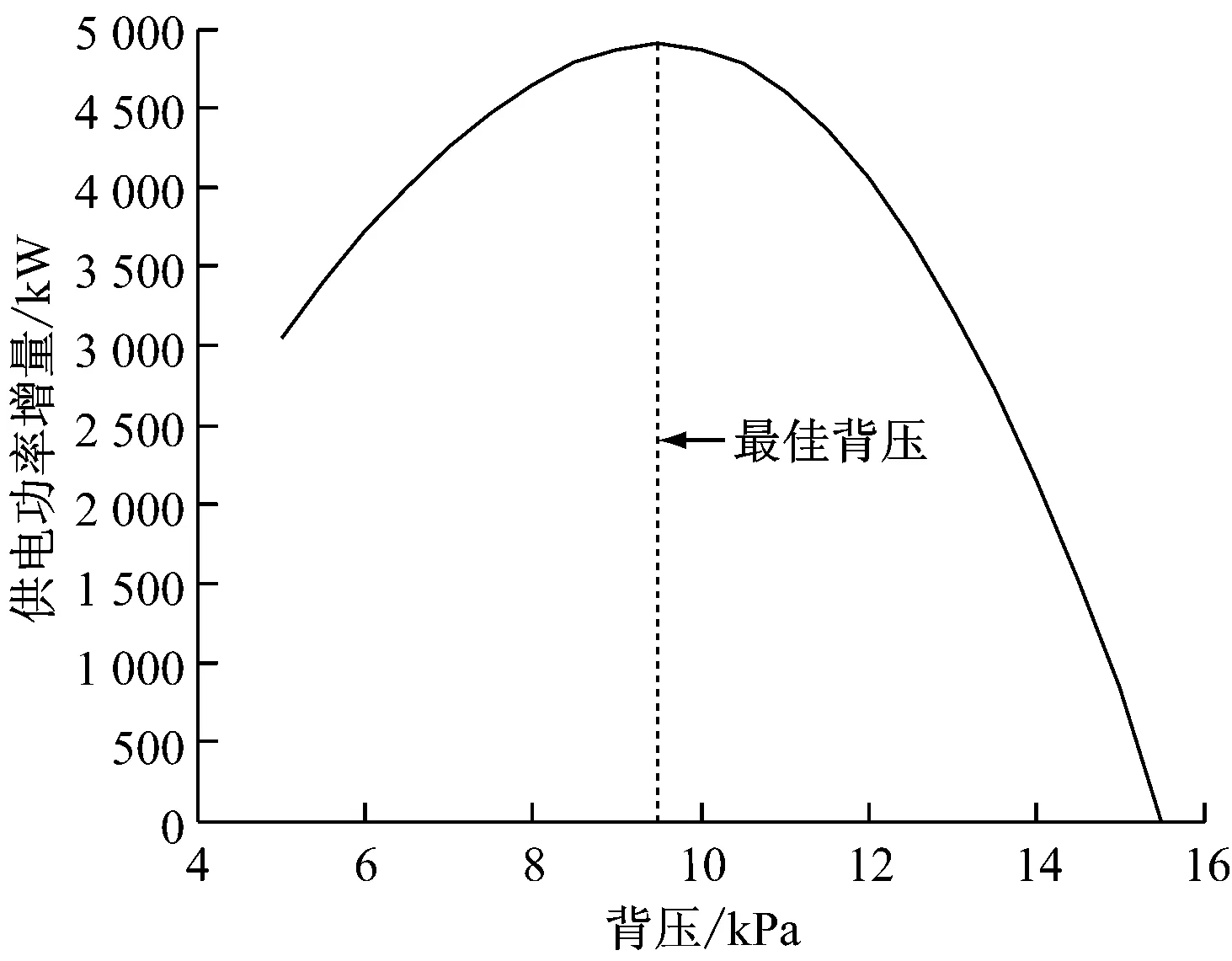
图4 供电功率增量与背压的关系曲线
同样对算法中的参数进行选取,拟合其他负荷段不同环境温度下的发电机功率-背压、空冷风机耗功功率-背压关系曲线,得出各工况下的最佳背压值,如表1~表3所示.
使用最小二乘法对表1~表3中的数据进行拟合得到各负荷段内最佳背压与环境温度的函数关系式(见表4),为了便于观察分析,将各函数曲线画于同一图中,如图5所示.
由图5可知,同一负荷段内,最佳背压随着环境温度的升高而升高,且环境温度越高,最佳背压升高的速率越快;当负荷较低,且环境温度较低时,最佳背压变化缓慢;环境温度较低时,最佳背压随负荷的变化不太明显,而环境温度较高时,最佳背压随负荷的升高而升高,在高负荷段时更加显著.
4实际应用
将最佳背压计算模型应用在某300 MW直接空冷机组上,对DCS中原有背压调节逻辑进行优化,利用分段线性函数,函数中参数按照表1~表3设置,以负荷和环境温度为输入,最佳背压为输出;添加1个背压选择模块,运行人员可根据机组实际运行状况在最佳背压与人为设定背压之间进行选取,将选取后的背压作为背压设定值送入PID中进行空冷风机转速调节.优化后的背压调节逻辑图如图6(a)所示,组态图如图6(b)所示.由于篇幅有限,仅对2个负荷段的最佳背压求取组态进行表示,实际应用中其他负荷段最佳背压的求取采用同样的方法即可.
表1180~<200 MW、200~<220 MW负荷段内不同环境温度下的最佳背压值
Tab.1Optimum back pressure corresponding to different ambient temperatures at 180-<200 MW and 200-<220 MW
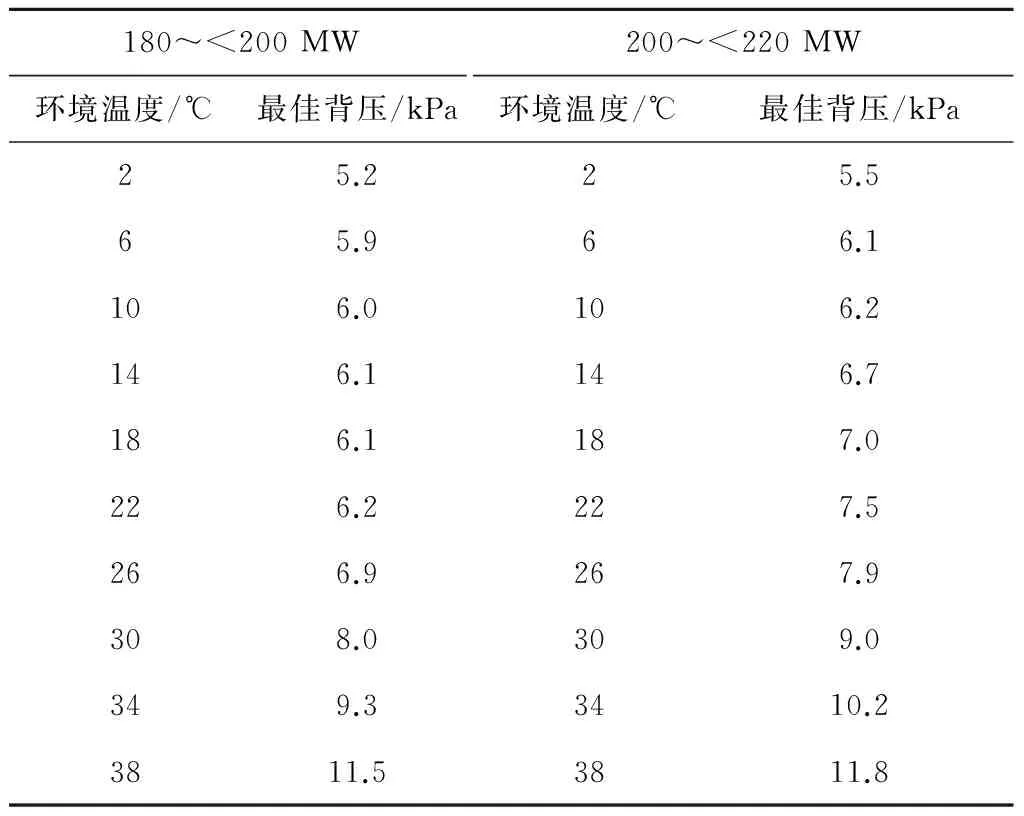
180~<200MW200~<220MW环境温度/℃最佳背压/kPa环境温度/℃最佳背压/kPa25.225.565.966.1106.0106.2146.1146.7186.1187.0226.2227.5266.9267.9308.0309.0349.33410.23811.53811.8
表2220~<240 MW、240~<260 MW负荷段内不同环境温度下的最佳背压值
Tab.2Optimum back pressure corresponding to different ambient temperatures at 220-<240 MW and 240-<260 MW
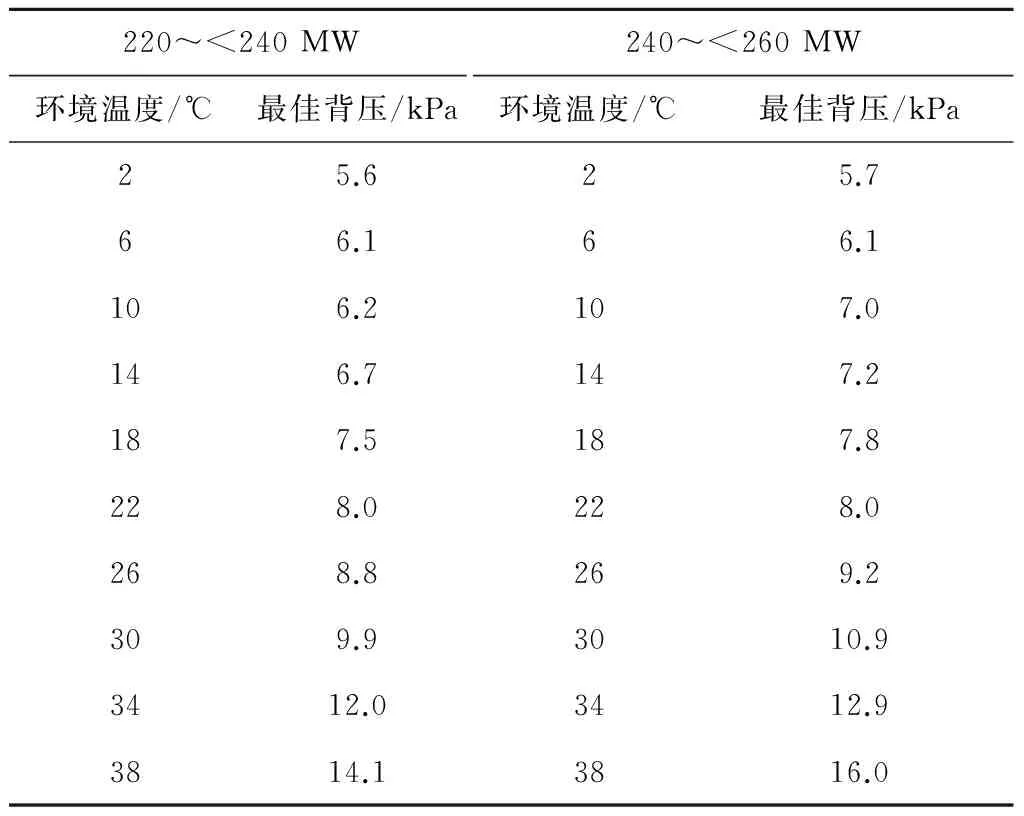
220~<240MW240~<260MW环境温度/℃最佳背压/kPa环境温度/℃最佳背压/kPa25.625.766.166.1106.2107.0146.7147.2187.5187.8228.0228.0268.8269.2309.93010.93412.03412.93814.13816.0
表3260~<280 MW、280~300 MW负荷段内不同环境温度下的最佳背压值
Tab.3Optimum back pressure corresponding to different ambient temperatures at 260-<280 MW and 280-300 MW
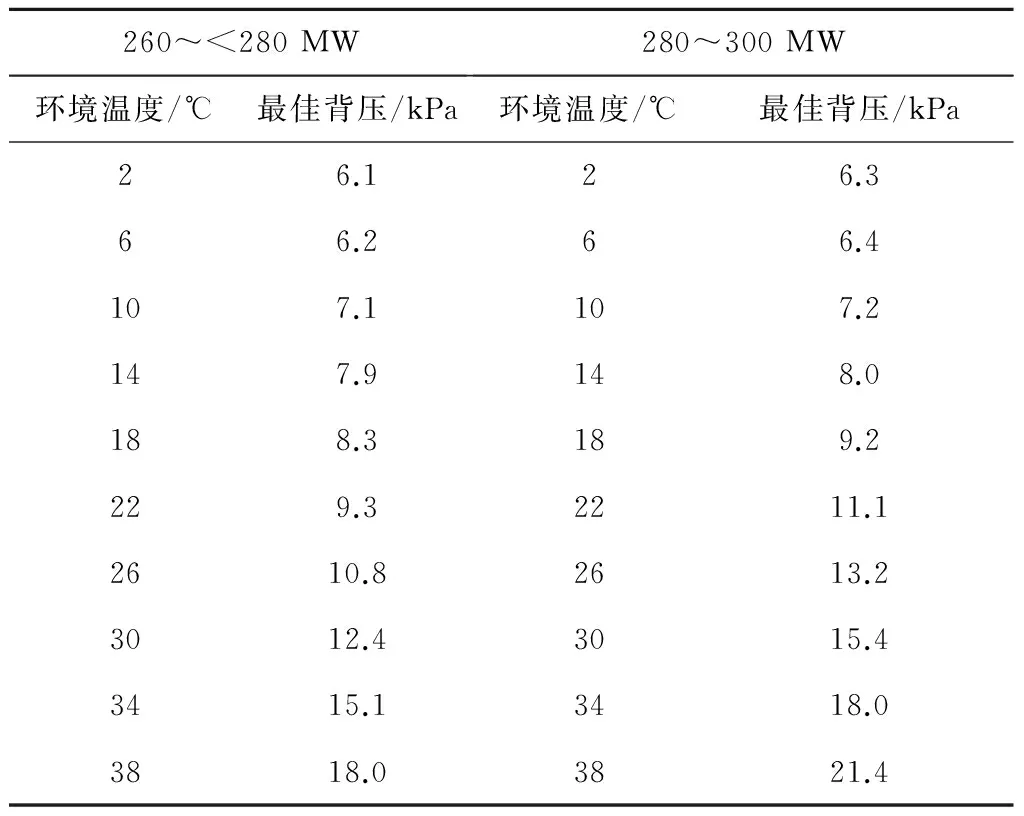
260~<280MW280~300MW环境温度/℃最佳背压/kPa环境温度/℃最佳背压/kPa26.126.366.266.4107.1107.2147.9148.0188.3189.2229.32211.12610.82613.23012.43015.43415.13418.03818.03821.4
当该直接空冷机组负荷稳定时,将空冷风机运行方式设置在自动控制状态下,并将背压设定值设为7.2 kPa,此时背压调节逻辑中PID控制器根据背压设定值和背压实际值的偏差进行计算,输出空冷风机转速总控指令来控制风机运行.稳定后,负荷维持在212.4 MW附近,空冷风机耗功功率维持在2 520 kW附近,背压实际值维持在7.2 kPa左右.此时,启用背压优化模式,机组参数变化曲线如图7所示.从图7可以看出,启用背压优化模式后,最佳背压高于当前背压实际值,背压调节逻辑通过PID控制减小空冷风机转速来提高背压.空冷风机转速减小,则空冷风机耗功功率减小,在此过程中,机组发电机功率波动很小,发电量损失较小.
表4各负荷段内最佳背压与环境温度的函数关系式
Tab.4Functional relationship between optimum back pressure and ambient temperature at different loads

负荷/MW最佳背压-环境温度函数关系式180~<200y=0.0004x3-0.0153x2+0.2266x+4.8874200~<220y=0.0002x3-0.0074x2+0.1665x+5.2210220~<240y=0.0002x3-0.0064x2+0.1509x+5.3025240~<260y=0.0004x3-0.0159x2+0.2927x+5.0822260~<280y=0.0003x3-0.0062x2+0.1787x+5.6211280~300y=0.0111x2-0.0308x+6.2805
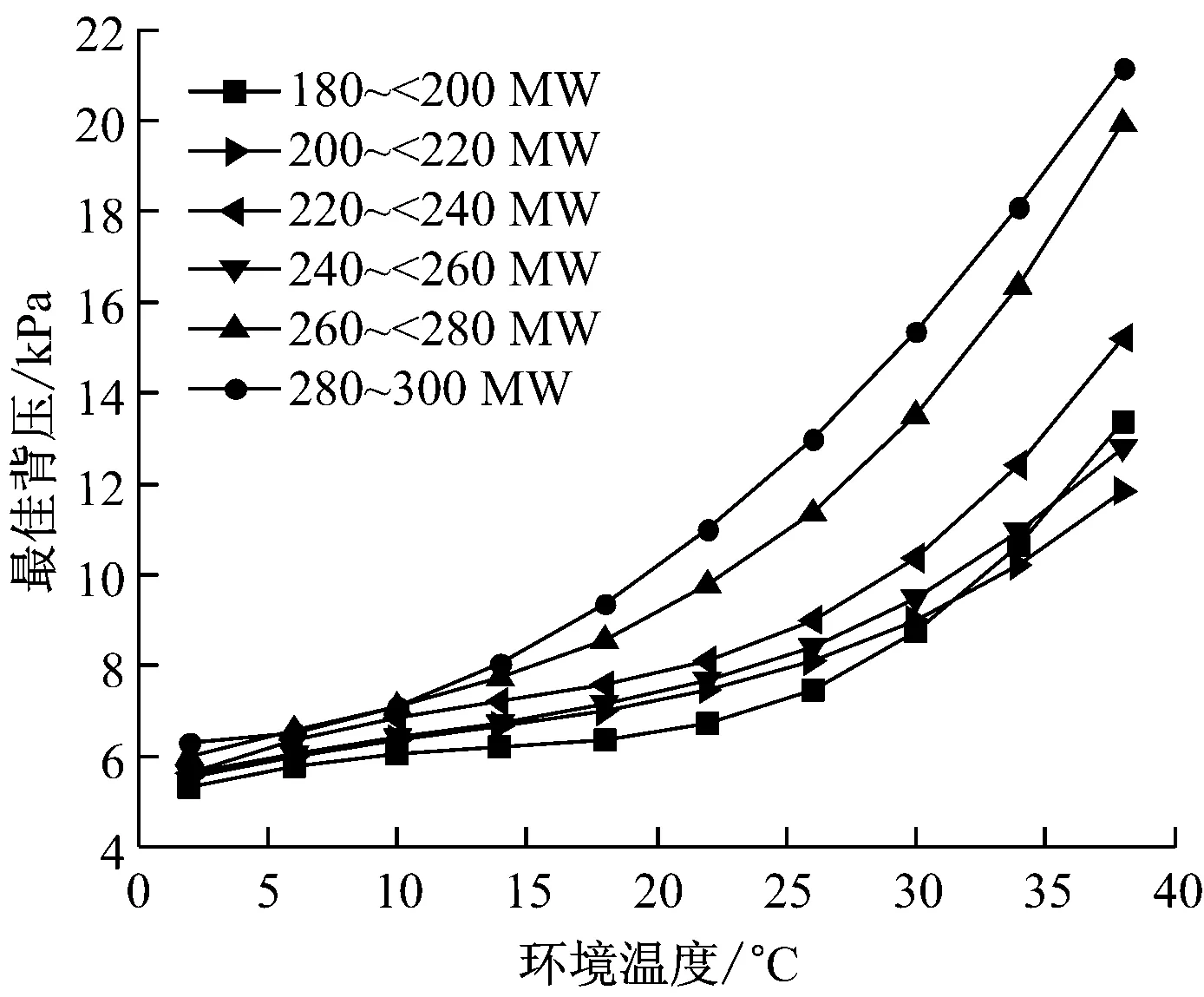
图5 各负荷段内最佳背压与环境温度的关系曲线
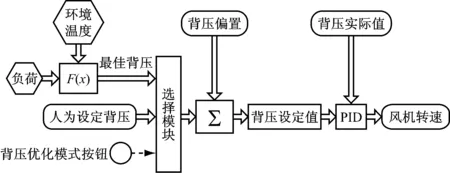
(a) 优化后的DCS背压调节逻辑图
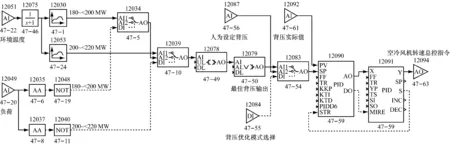
(b) 优化后的DCS背压调节组态图
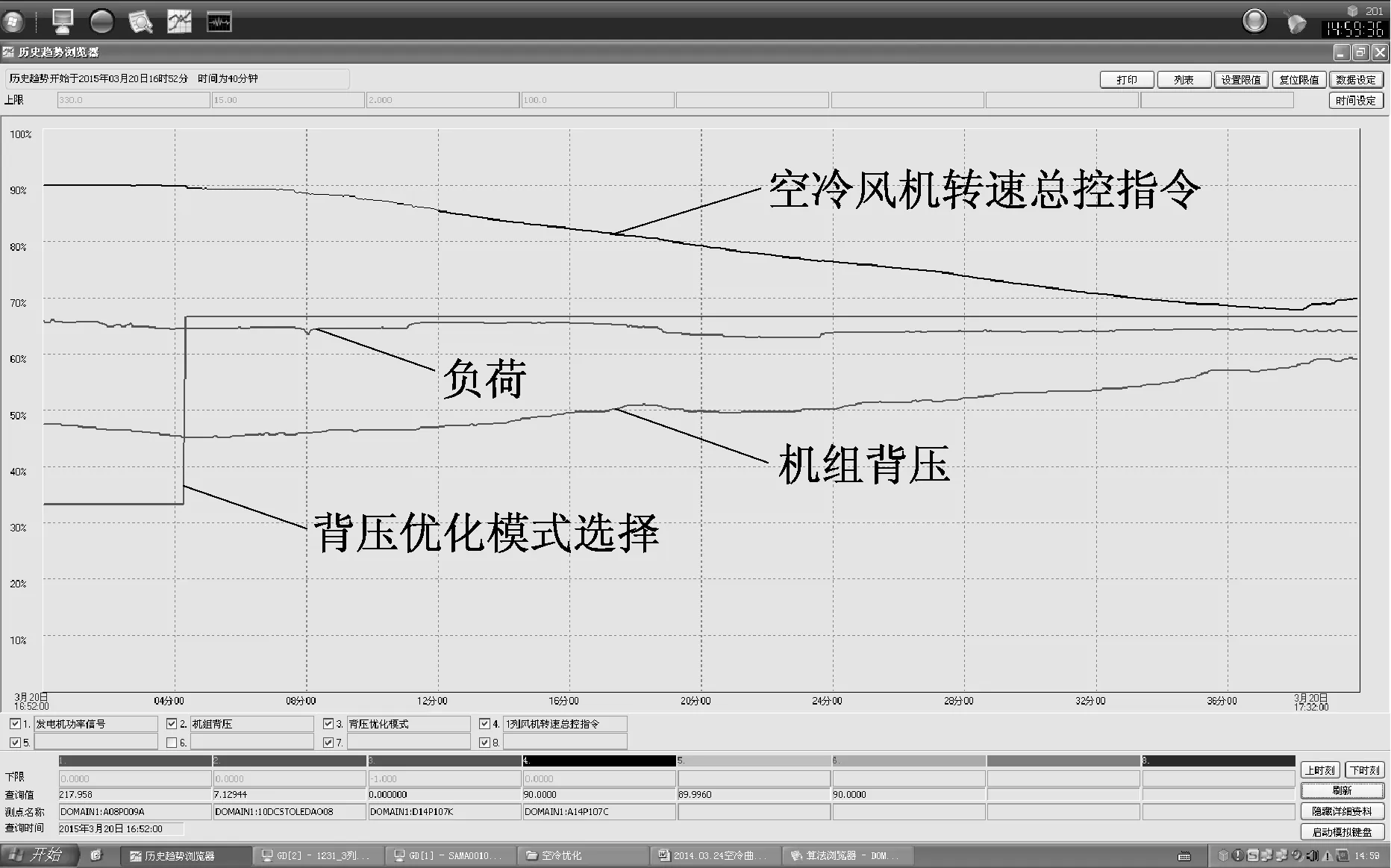
图7 启用背压优化模式后的机组运行曲线
从机组SIS数据库中导出启用背压优化模式后的机组实际运行数据,画出背压、发电机功率和空冷风机耗功功率的变化曲线(见图8).由图8可知,启用背压优化模式后,发电机功率损失约890 kW,而空冷风机耗功功率减小约1 400 kW,供电功率增量平均为510 kW.最佳背压的应用在保证机组安全平稳运行的前提下提高了机组经济效益.
需要特别说明的是,最佳背压的应用在春秋季节对机组效益的提高意义最大.冬季低温环境下,空冷风机基本处于停运状态,此时通过调整空冷风机转速已无法实现降低背压的目的;另外,环境温度很低时,空冷凝汽器面临冻结的危险,出于防冻考虑,也不能无限制地降低背压[13].夏季高温环境下,空冷风机基本处于满频运行状态,已无调节裕度,机组只能在高背压下运行,为保证安全,必要时还需降低负荷,此时可考虑采用喷淋[14]等其他手段来降低背压.
5结论
(1) 直接空冷机组的背压受多种因素的综合影响,其中负荷、环境温度和空冷风机运行方式对最佳背压的影响最为显著.
(2) 直接空冷机组背压的选择直接影响其经济性,机组在最佳背压下运行时供电功率增量最大.
(3) 在各工况下运行时,直接空冷机组存在某一确定的最佳背压值,但该值随着负荷和环境温度的变化而变化.最佳背压随着负荷和环境温度的升高而升高,且环境温度越高,最佳背压升高的速率越快;当环境温度较低时,最佳背压受负荷的影响较小.
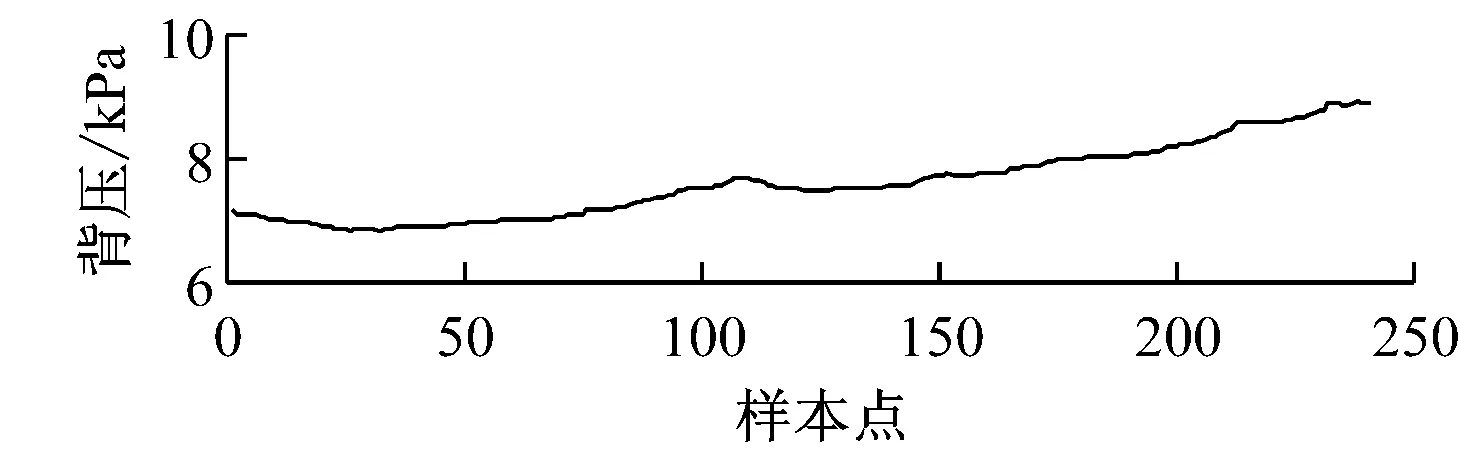
(a)
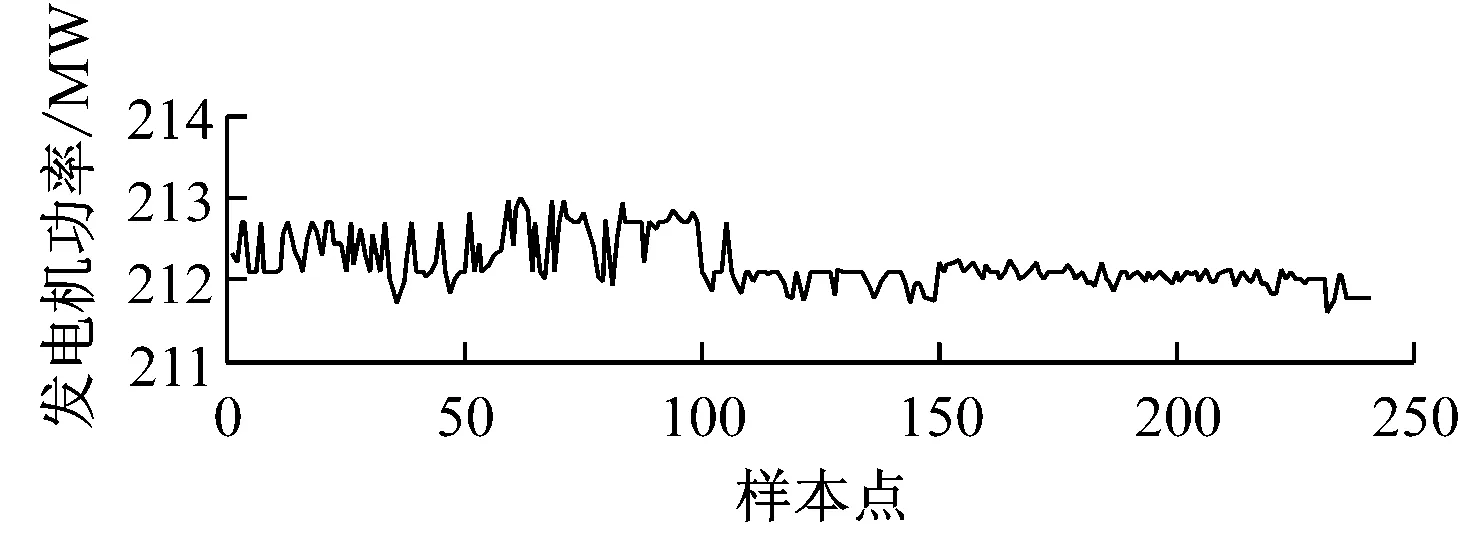
(b)
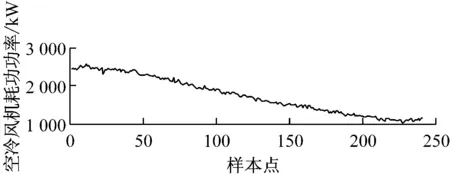
(c)
(4) 最佳背压在春秋季节的应用可在保证机组稳定运行的前提下,提高经济效益.
参考文献:
[1]张学镭,王金平,陈海平.环境风影响下直接空冷机组排汽压力的计算模型[J].中国电机工程学报,2012,32(23):40-41.
ZHANG Xuelei,WANG Jinping,CHEN Haiping.A calculation model of exhaust pressure of direct air-cooled units considering the effect of environmental wind[J].Proceedings of the CSEE,2012,32(23):40-41.
[2]高建强,陈冠兵,薛楠楠.直接空冷机组经济背压计算模型及其应用[J].动力工程学报,2014,34(2):153-154.
GAO Jianqiang,CHEN Guanbing,XUE Nannan.Calculation model for economic back pressure of direct air-cooling unit and its application[J].Journal of Chinese Society of Power Engineering,2014,34(2):153-154.
[3]赵洪滨,曹岭.直接空冷凝汽器理论最佳背压的研究[J].工程热物理学报,2009,30(11):1834-1836.
ZHAO Hongbin,CAO Ling.Theoretical study on the optimal back-pressure of a direct air-cooled condenser[J].Journal of Engineering Thermophysics,2009,30(11):1834-1836.
[4]郭民臣,谢静岚,李鹏.变工况下直接空冷机组最佳真空的分析[J].动力工程学报,2012,32(7):542-546.
GUO Minchen,XIE Jinglan,LI Peng.Analysis on optimum vacuum of direct air-cooled unit under variable working conditions[J]. Journal of Chinese Society of Power Engineering,2012,32(7):542-546.
[5]金秀章,许铁,张建辉.300 MW机组空冷岛温度监测系统的设计[J].计算机仿真,2013,30(11):112-113.
JIN Xiuzhang,XU Tie,ZHANG Jianhui. Design of air-cooled island temperature monitoring system for 300 MW unit[J]. Computer Simulation,2013,30(11):112-113.
[6]严俊杰,张春雨,李秀云,等.直接空冷系统变工况特性的理论研究[J].热能动力工程,2000,15(6):601-603.
YAN Junjie,ZHANG Chunyu,LI Xiuyun,etal.Theoretical research on the off-design performance of a direct air-cooled system[J].Journal of Engineering for Thermal Energy and Power,2000,15(6):601-603.
[7]曹丽华,金建国,李勇.背压变化对汽轮发电机组电功率影响的计算方法研究[J].汽轮机技术,2006,48(1):11-13.
CAO Lihua,JIN Jianguo,LI Yong.Study on calculation method of the affection of back pressure to electric power of turbo-generator set[J].Turbine Technology,2006,48(1):11-13.
[8]邱丽霞,郝艳红,李润林,等.直接空冷汽轮机及其热力系统[M].北京:中国电力出版社,2006.
[9]杨立军,杜小泽,杨勇平.空冷凝汽器全工况运行特性分析[J].中国电机工程学报,2008,28(8):24-28.
YANG Lijun,DU Xiaoze,YANG Yongping.Performance analysis of air-cooled condensers at all operating conditions[J]. Proceedings of the CSEE,2008,28(8):24-28.
[10]曹旭,胡洪华,臧瑞起.直接空冷机组空冷岛优化运行研究[J].热力发电,2011,40(8):6-7.
CAO Xu,HU Honghua,ZHANG Ruiqi.Study on operation optimization of air-colled island for direct air-cooled units[J]. Thermal Power Generation,2011,40(8):6-7.
[11]奉国和.SVM分类核函数及参数选择比较[J].计算机工程与应用,2011,47(3):123-124.
FENG Guohe. Parameter optimizing for support vector machines classification[J]. Computer Engineering and Applications,2011,47(3):123-124.
[12]戴上平,宋永东.基于遗传算法与粒子群算法的支持向量机参数选择[J].计算机工程与科学,2012,34(10):114-116.
DAI Shangping,SONG Yongdong.Parameter selection of support vector machines based on the fusion of genetic algorithm and the particle swarm optimization[J].Computer Engineering & Science,2012,34(10):114-116.
[13]韩玉霞,张嘉英,李鑫,等.典型300 MW直接空冷供热机组冬季防冻措施分析[J].电站系统工程,2011,27(3):37-39.
HAN Yuxia,ZHANG Jiaying,LI Xin,etal. Anti-freezing protection of 300 MW direct air-cooling thermal power unit[J]. Power System Engineering,2011,27(3):37-39.
[14]赵爽,李西军.喷雾解决直接空冷机组夏季出力受阻的经济性分析[J].电站系统工程,2012,28(6):53-54.
ZHAO Shuang,LI Xijun.Economic analysis of spray cooling solving output limit of direct air-cooling unit in summer[J]. Power System Engineering,2012,28(6):53-54.
Calculation Method for Optimum Back Pressure of Direct Air-cooling Unit and Its Application
ZHAIYongjie,MILu,LIUJinlong
(Department of Automation, North China Electric Power University, Baoding 071003,Hebei Province, China)
Abstract:By analyzing the main factors that affect the back pressure of a direct air-cooling unit, and based on its historical data, a calculation model was set up for optimum back-pressure of the unit using support vector machine and particle swarm algorithm, so as to study the relations of back pressure with both the generator power and the power consumption of air-cooling fan. Taking a 300 MW direct air-cooling unit as the object of study, the optimum back pressure corresponding to different loads and ambient temperatures was calculated with the model, while a scheme for optimization of the back pressure was designed in DCS, and the optimized back pressure was then put into the adjusting logic of back pressure to regulate the controller. Results show that the optimum back pressure of direct air-cooling unit increases with the rise of load and ambient temperature. The application of optimum back pressure can help to increase the unit economy under the premise of ensuring safe and stable operation of the unit.
Key words:direct air-cooling unit; optimum back pressure; generator power; power consumption of air-cooling fan; support vector machine
收稿日期:2015-08-28
修订日期:2015-11-02
基金项目:中央高校基本科研业务费专项资金资助项目(2014MS140)
作者简介:翟永杰(1972-),男,河南漯河人,副教授,博士,主要从事火电厂自动控制、分散控制系统、智能计算等方面的工作.
文章编号:1674-7607(2016)07-0575-08中图分类号:TK262
文献标志码:A学科分类号:470.30
米路(通信作者),男,硕士研究生,电话(Tel.):15200091361;E-mail:15200091361@163.com.
